基于PCA和LMD分解的滚动轴承故障特征提取方法

黄 浩，吕 勇，肖 涵，侯高雁

(武汉科技大学，冶金装备及其控制教育部重点实验室，湖北武汉 430081)



基于PCA和LMD分解的滚动轴承故障特征提取方法

黄 浩，吕 勇，肖 涵，侯高雁

(武汉科技大学，冶金装备及其控制教育部重点实验室，湖北武汉 430081)

局部均值分解(LMD)是一种自适应时频分析方法，并在轴承的故障诊断中成功应用，但是受噪声的影响比较大。为了最大程度地降低噪声的干扰，提出了主分量分析(PCA)与局部均值分解(LMD)相结合的故障诊断方法。该方法首先利用相空间重构将一维时间序列振动信号嵌入为等效的多维时间序列信号，然后利用主分量分析提取主要成分实现降噪，最后把降噪之后的信号进行LMD分解，分解成若干个乘积函数(PF)之和，对能量最高的PF1进行包络谱分析，提取出故障特征信息。通过仿真试验和轴承故障试验，结果表明该方法能够有效地提取出信号的故障特征，证明了该方法的有效性。

相空间重构；主分量分析；LMD；特征提取

0 引言

故障诊断的关键是从原振动信号中提取故障特征，其中时频分析方法是提取故障特征的主要方法之一。局部均值分解(LMD)[1-2]是Smith提出的一种自适应时频分析方法，该方法能够有效地处理非线性、非平稳信号，近几年在故障诊断中取得了较好的效果。在实际应用中，振动信号往往受到系统噪声和环境噪声的干扰。当信号的信噪比较小时，噪声会使得LMD分解层数增加，无法正确分解出乘积函数(PF)分量，严重时还会使LMD失去实际的物理意义。因此，在进行LMD分解之前有必要进行降噪处理。相空间重构可以将一维时间序列重构到等效的多维相空间[3-4]，并利用相关的方法对多维信号进行处理，实现降噪。吕勇等[5]提出了加权相空间重构算法，并运用于齿轮故障诊断中，取得很好的降噪效果；徐洪涛等[6]利用相空间重构和主分量分析结合的算法对遥测信号进行了降噪,有效的去除了信号的噪声。基于以上研究，文中首先利用相空间重构和主分量分析结合的方法对信号进行降噪处理，然后进行LMD分解，这样就降低了噪声对LMD分解的影响，提高了LMD的分解能力，再从PF分量中提取出故障特征，并将该方法应用于滚动轴承故障信号分析中，成功提取出了信号的故障特征。

1 基于PCA与LMD的特征提取方法

1.1 相空间重构

Takens等[4]证明了重构后的维相空间与系统的动力学是微分同胚的。在故障诊断中，大多数非线性振动信号重构成高维相空间，故障状态下的系统动力学特征更能清晰地突显。设X=(x0,x1,…,xn)为一维时间序列，选择合适的嵌入维数m和延迟时间τ，重构的相空间可以表示成

Χi=(xi-(m-1)τ，xi-(m-2)τ,…,xi)

(1)

式中Xi为第i个相点。

若要将一维时间序列信号重构到高维时间序列信号，则需要求得其嵌入维数m和延迟时间τ，时间延迟τ和嵌入维数m的正确选择是相空间重构的重要前提。时间延迟由互信息法确定，具体计算步骤参照文献[7]。求得τ之后，再用Cao氏方法求嵌入维数，具体计算步骤参照文献[8]。

1.2 主分量分析(PCA)

主分量分析是用少数的特征来描述样本空间并降低样本空间维数的方法[9]，并且广泛应用于数据的压缩和降噪处理中。给定一个n维向量X=(x0,x1，…，xn)，它对应于样本空间的一点，且存在一正交函数集A，使得

Y=(y1,y2,…,yn)=XA

(2)

求Y的转置矩阵：

YT=XTAT

(3)

将式(2)与式(3)相乘并取数学期望

E(YYT)=AE(YYT)AT

(4)

令Cx和Cy分别为和的协方差矩阵，式(4)可以表达为

Cy=ACxAT

(5)

选取合适的A，可以使各分量yi(i=1,2…,n)相互之间的协方差为零，并使Cy为对角阵，即

Cy=diag(λ1，λ2，…，λn)

(6)

yi称为主分量,λi为Cy的特征值，也为Y的主元素。经过上述变换，原向量X各分量之间的相关性已经被消除了。根据信息论原理，将λi按从大到小的顺序排列，当

(7)

时，选取前m个主分量对应的新向量Y=(y1,y2,…ym)取代原向量X，这样X中的各样本投影到子空间后投影分量的平均信息量最大。因此，主分量分析能够降低空间维数，突出有用信息，并且去除冗余信息。

1.3 局部均值分解(LMD)

从本质上讲，LMD时频分析方法就是把原始信号分解成一系列PF分量，每1个PF分量由1个包络信号和1个纯调频信号的乘积而得，对于原始信号x(t)，LMD分解具体步骤参考文献[1]。经过LMD分解后，原始信号x(t)分解为k个PF分量和uk(其中uk为残余项)之和，即:

(8)

1.4 方法步骤

相空间重构将一维信号重构为多维信号，更能清晰地突显故障状态下的系统动力学特征，利用主分量分析对多维信号进行降噪处理，并还原为一维信号，这样就提高了信号的信噪比，减小了噪声对LMD分解的影响。具体步骤如下：

(1)用互信息法求出原始信号的延迟时间τ，用Cao的方法求出原始含噪信号的嵌入维数m；

(2)通过确定的嵌入维数m和延迟时间τ来构建相空间；

(3)对构建的m维相空间作主分量分析，实现原始信号的降噪；

(4)对降噪之后的信号进行LMD分解，得到PF分量和残余项uk；

(5)选择能量最高的PF1进行包络谱分析，提取特征信息。

提出方法的基本流程图如图1所示。

图1 提出方法的流程简图

2 数值仿真试验

为了验证提出方法的有效性，用采样频率为2 000 Hz，采样点数为2 000的仿真信号进行分析，仿真信号如下:

x(t)=[1+cos(10πt)]sin(20πt)+sin(80πt)+n(t)

(9)

式中n(t)为有效值为1的均匀白噪声。

图2为仿真信号的时域图，图3为其频谱图，图4为对其进行LMD分解之后得到的乘积函数(PF)分量及残余项(u)结果图。

图2 仿真信号的时域图

图3 仿真信号的频谱图

图4 仿真信号的LMD分解

对仿真信号进行降噪处理，首先建立仿真信号的相空间，根据相空间构建定理需要确定延迟时间τ和嵌入维数m。

图5为用互信息法计算仿真信号的延迟时间，I(τ)表示交互信息，I(τ)的第一个极小值对应的τ为选择的时间延迟[7],从图中可以得到I(τ)的第一个极小值点是2，则相空间的延迟时间τ=2 s。

图5 互信息法求时延

图6 Cao氏方法求嵌入维数

图6是用Cao氏方法求嵌入维数，纵坐标E表示嵌入维数从m变化到m+1的距离相对增量[7]，E1(m)是一个统计量,表示为

(10)

当E1(m)无变化或变化缓慢时所对应的m即为嵌入维数。图中纵坐标E2表示E(m+1)，E1表示E(m)。从图上可以看出，当m≥10时，E1(m)的值不再随m的增加而增加，则嵌入维数可以取为10。

由选取的延时时间τ和嵌入维数m便可建立仿真信号的相空间，然后利用PCA方法对仿真信号的相空间进行分析，选取特征值较大的主分量进行重构，达到消除噪声的效果。图7为对仿真信号进行PCA降噪后的信号时域图，图8为降噪后信号的频谱图，图9为降噪后信号进行LMD分解之后的结果图。

图7 降噪后信号时域图

图8 降噪后信号频谱图

对比图8和图3，通过观察降噪后信号的频谱图和降噪前信号的频谱图，可以看到降噪后仿真信号的噪声得到了较好的消除。对比图9和图4，降噪后信号的LMD分解层数减少了，说明LMD的分解能力得到了提升。因此PCA与LMD相结合的分解方法能够有效降低噪声成分对LMD分解的干扰，突出信号的主要特征，提高LMD的分解能力。

3 应用实例

图9 降噪后信号的LMD分解

本文采用美国凯西斯西储大学轴承试验数据进行分析[10]。试验数据中采用6205-2RS型深沟球轴承，其参数分别是轴承节径D=39.04 mm，滚动体直径d=7.94 mm，滚动体个数Z=9，接触角为0°，发动机转速1 750 r/min，采样频率为12 000 Hz。计算可知，转轴基频为fτ=29.17 Hz，内圈故障频率f=157.94 Hz，从采集的数据中选2 048个点进行研究。

图10(a)为轴承故障信号时域图，图10(b)为轴承故障信号频谱图，采用主分量分析对原始轴承信号进行降噪，用互信息法计算得延迟时间τ=1 s，用Cao氏方法计算得嵌入维数m=14，使用所得的和进行相空间重构，再对重构后的高维信号进行主分量分析降噪，降噪结果如图10(c)所示。图10(d)为降噪之后的信号频谱图，对比降噪之前的频谱图可以看到，低频成分和噪声成分已经滤去，噪声得到了较大的削减。图10(e)是降噪之后的信号经LMD分解得到的PF1分量，对PF1进行包络谱分析，其谱图在0～400 Hz范围内，如图10(f)所示。从图中可以看到故障频率已经显现出来，其中在频率158.2 Hz有明显的峰值，这和内圈的理论值157.94 Hz非常接近。由于受到轴承内圈参数误差等的影响，可以认为158.2 Hz就是轴承的内圈故障特征频率，同时在频率58.6 Hz处也有明显的峰值，这和转轴基频的2倍频58.34 Hz非常接近，频率158.2 Hz的2倍频316.4 Hz处的峰值也很明显。因此，可以判断出轴承出现了内圈故障。本文提出的方法能提取出轴承信号中所包含的故障成分，说明了此方法的可行性。

(a)滚动轴承信号时域图

(b)滚动轴承信号频谱图

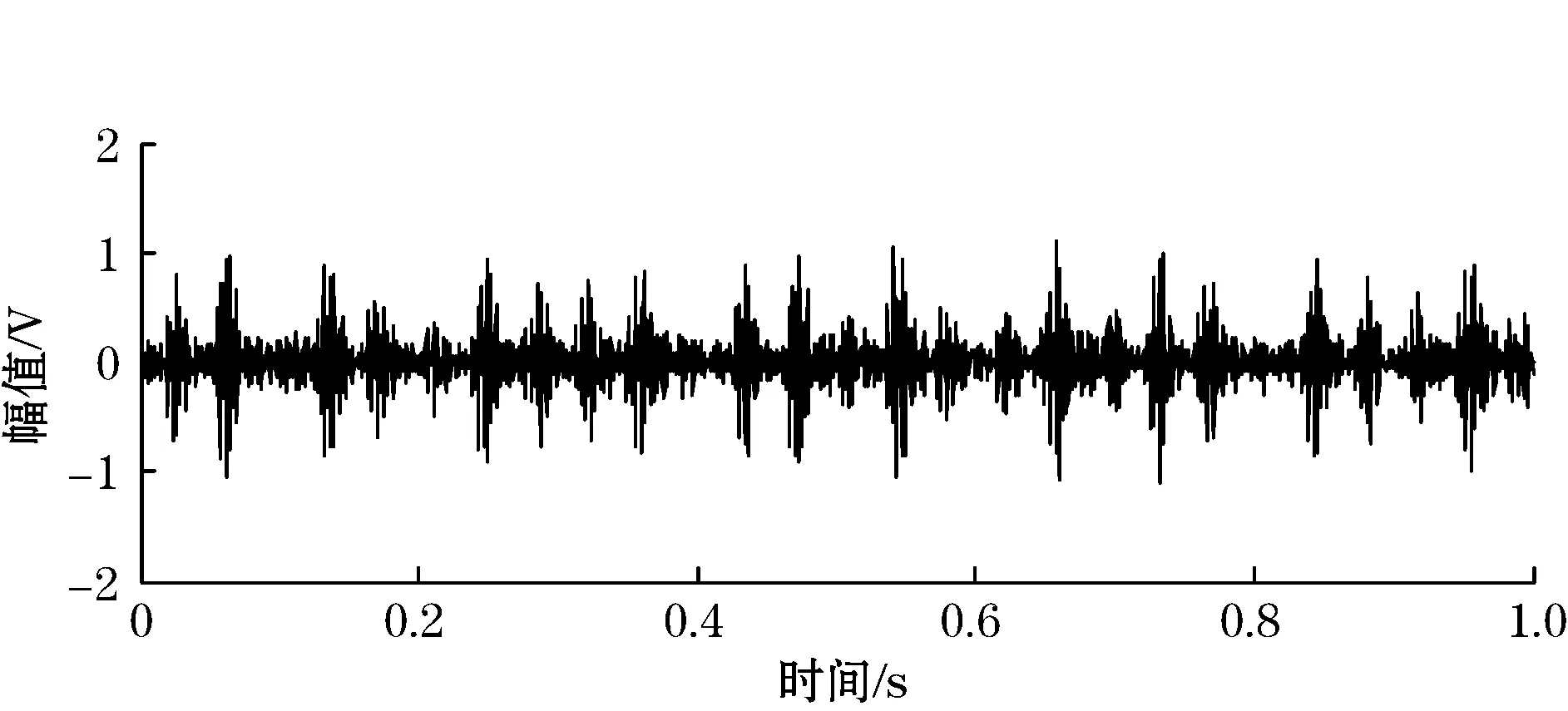
(c) 经主分量降噪后信号的时域图

(d)经主分量分析降噪后的信号频谱图

(e)降噪后的信号进行LMD分解得到的PF1

(f)PF1的包络谱图10 信号经主分量分析降噪与LMD分析结果图

4 结论

经过以上分析，可以得出主分量分析降噪方法能够有效地去除信号中的噪声成分，提高信号的信噪比，突出信号中的有用成分，降低噪声对LMD分解的影响。将降噪之后的信号进行LMD分解之后，对第一个分量PF1进行包络谱分析，能有效地提取故障特征，并判断出机械故障的类别。

[1] SMITH S J．The local mean decomposition and its application to EEG perception data.Journal of the Royal Society Interface， 2005，2(5)：443-454．

[2] 侯高雁，吕勇，李友荣，等．LMD形态学与FEMD形态学在故障中的对比研究．仪表技术与传感器，2014(8)：107-110．

[3] MICHAEL T J,RICHARD J P.Generalized phase space projection for nonlinear noise reduction.Physica D,2005:306-317.

[4] TAKENS F.Detecting stranger attractors in turbulence． Dynamical Systems and Turbulence.Berlin:Springer-Verlag,1981:366-381.

[5] 吕勇，李友荣，徐金梧.加权相空间重构降噪算法及其在设备故障诊断中的应用.机械工程学报,2007,43(7):158-161.

[6] 徐洪涛,王跃刚.基于相空间重构和主分量分析的遥测信号噪声消除.计算机应用，2010,30(3):793-795.

[7] 苑宇，马孝江.基于主分量分析的柴油机振动信号特征提取.中国机械工程，2007，18(8):971-974.

[8] CAO L Y.Practical method for determining the minimum embedding dimension of a scalar time series.Physica D,1997,110:43-50.

[9] 俞星，尹洪胜，张敏.基于主分量和小波分析的煤矿主通风机故障诊断研究.煤矿机械，2010,31(4):238-240.

[10]Case Western Reserve University．Case western reserve university bearing data center website [EB/OL].[2011-05-03]．http://www.eecs.case.edu/ laboratory/bearing/．

Feature Extraction Method of Rolling Bearing Fault Based on Principal Component Analysis and Local Mean Decomposition

HUANG Hao ,Lü Yong ,XIAO Han ,HOU Gao-yan

(Wuhan University of Science and Technology，Wuhan 430081,China)

Local mean decomposition(LMD) is an adaptive time-frequency analysis method,which is successfully used in rolling bearing fault diagnosis but strongly influenced by noise.In order to reduce the noise interference to the greatest extent,a fault diagnosis method based on principal component analysis(PCA) and local mean decomposition(LMD) was proposed.Firstly,one-dimension time series vibration signals were embedded to equivalent multi-dimensions through the reconstructed phase space.Then,available component was extracted by PCA,achieving the effect of noise reduction.Finally,the de-noised signal was decomposed by LMD and can be represented as the sum of the product functsons.The component PF1 which contains the highest power was selected to conduct the envelope spectrum analysis and the fault features were exacted.The results show that the method can effectively extract the fault features through the analysis of the simulation signal and the rolling bearing fault diagnosis data experiment,proving the effectiveness of the proposed method.

reconstructed phase space ; PCA ; LMD; feature extraction

国家自然科学基金青年基金资助项目(51105284)；湖北省高校优秀中青年创新团队计划(T200905)资助

2014-03-04 收修改稿日期：2014-11-07

TH165

A

1002-1841(2015)04-0076-03

黄浩(1989 —)，硕士研究生，主要研究方向为信号处理。E-mail:516554097@qq.com 吕勇(1976—)，教授，博士生导师，主要从事故障诊断与监测。E-mail：lvyong@wust.edu.cn