金属感应式落球法液体黏度系数测量方法研究

杨志军，尹文庆，卢 伟,蔡婷婷，赵贤林

(1.南京农业大学工学院，江苏省农业智能化装备重点实验室，江苏南京 210031；2.东南大学电气工程学院，江苏南京 210096)



金属感应式落球法液体黏度系数测量方法研究

杨志军1，尹文庆1，卢 伟1,蔡婷婷2，赵贤林1

(1.南京农业大学工学院，江苏省农业智能化装备重点实验室，江苏南京 210031；2.东南大学电气工程学院，江苏南京 210096)

粘度系数是反映液体理化特性的一个重要参数，为了解决现有液体黏度系数测量仪器测量误差大且难以准确测量非透明液体等问题。提出一种基于电涡流效应的金属感应式落球法测量液体黏度系数的测量方法。采用金属感应非接触地测量出小球下落的位移与时间，可以实现非透明液体黏度系数的测量，同时针对现有落球法中由于小球直径小而无法精确感应的问题，提出采用大直径金属球进行测量，推导验证出大直径金属球下落时液体黏度系数的计算公式，最后进行了仿真和实验研究，实验结果表明，测量准确度在98%以上，且重复性好。

粘度系数；金属感应；落球法；非接触测

0 引言

液体黏度是液体的重要特征和属性之一[1]。每种实际液体都具有不同程度的粘滞性，当液体流动时,平行于流动方向的各层流体速度是不同的，即液体流动时存在着摩擦阻力，我们称这一摩擦阻力为粘滞力[2]。粘滞力作为一个矢量，其方向平行于接触面，大小与速度梯度及接触面积成正比[3]。液体中η表征液体粘滞性强弱的一个重要参数为，称为液体黏度系数[4]。粘度系数在农业技术、工业生产、医疗救治、石油提炼和科学研究中都具有一定的实际意义[5]。因此，在实际应用中，液体黏度系数的精确测量显得十分重要[6]。

目前液体黏度的测量主要采用金属小球，通过实验发现金属小球的直径变化能够对实验结果产生较大的相对误差[7]。现有测量液体粘滞系数的方法有很多种[8]，主要有毛细管测量法、旋转测量法、落针测量法、落球法等[9]。毛细管法制造简单，成本低，操作也相对简单[10]，但是易被颗粒物堵塞，不适合在高温下使用，从而影响其测量精度[11]。旋转法主要是通过测量流体作用于物体的粘性力矩和物体的转速从而计算测量物体的粘度系数，适用范围较宽，测量方便，但由于测量误差较大，测量结果一般为相对值，导致在精确测量中一般很少使用此方法[12]。落针法采用的是在测量装置的两端放置磁铁，该方法在测量时通过落针在液体中由于前后两个磁铁的磁性差异下落，但是由于落针下落的方向偏移等原因造成该方法在测量过程中误差较大且重复性不理想[13]。目前，液体黏度的测量也是大学物理实验中的重要内容之一[14]。其测量方法很多,具有代表性的传统方法是落球法[15]。落球法适合粘度较大且有一定透明度的液体，实验中通常采用手控计时来测定小球匀速下落的速度，所以要求小球下落的速度要尽可能慢,因而需要小球的直径要尽可能小,待测液体的粘度要尽可能大,这就给落球法测液体黏度带来许多限制条件[16]。同时，传统的落球法液体黏度系数测定仪，采用的是人工计时。人工秒表计时有视觉误差和反应误差，导致实验所得小球下落时间测量不准确[17]。目前在粘度测量方法研究过程中，已经出现了采用单片机进行计时的智能型落球法液体黏度测量仪，从而有效地减小了测量中人为的误差。当前检测落球的方法有激光法和CCD法。激光法是通过检测落球遮挡住激光时，光电接收器信号发生突变开始计时，但由于落球法中采用的小球直径较小使得激光难以对准和调节光电门激光束复杂，所以激光法目前使用范围较小，而CCD法则采用CCD摄像头检测小球的下落位置进行计时，装置成本较高，并且摄像头被油污污染后影响测量精度[18]。

基于上述研究方法和理论基础，本文基于电磁学原理中的电涡流效应[19-20]，拟采用金属线圈感应的方法，非接触的测量和计算落球下落的时间和位移，分析不同球径对液体黏度系数的影响，最终推导出大直径金属球在液体黏度系数测量过程中的通用计算公式，从而解决了传统落球法中对小球直径和液体透明度的限制。同时独创地采用非接触式金属线圈感应的方法准确计时，最终对通用公式进行仿真和实验的比较研究。

1 仪器结构

1.1 金属感应式液体黏度测量装置设计

感应式液体黏度测量仪结构如图1所示。其特征为：在盛满待测液体的玻璃量筒的外壁相隔0.31 m处平行地套上两个金属感应线圈，使得金属球在待测液体中下落过程中能够依次穿过这两个感应线圈。当金属球穿过感应线圈时，可引起线圈电感参数的变化，将这两个感应线圈的引出线与处理器相连，处理器通过对线圈电感参数变化信号的处理，实现准确计时。最后代入相应的量筒和待测液体高度、线圈间距离、金属球直径、金属球和液体的密度等参数，可精确地实现金属球下落速度的测量和液体黏度的计算。从而降低了测量液体黏度实验的难度，提高了实验的效率，并且不受液体透光程度的影响。

图1 仪器结构示意图

1.2 金属感应检测电路设计

金属球的检测采用电涡流原理,电涡流检测是利用金属球接近感应线圈中间时，因为涡流产生使得感应线圈的电感发生变化，从而实现非接触金属感应测量，具体检测电路原理框图如图2所示。

图2 非接触金属感应检测原理

如图3所示，具体检测电路由3部分组成：电容反馈式正弦波自激振荡电路、金属感应检测电路和信号放大输出电路。

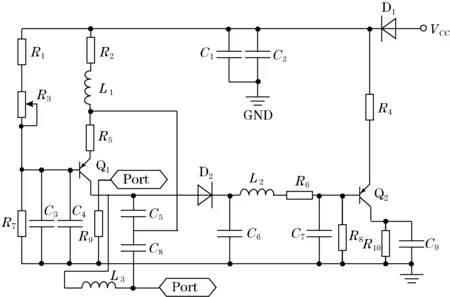
图3 金属感应线圈测量检测电路

电路中左侧部分是由三极管和电容构成的电容反馈式正弦波自激振荡电路，该振荡电路形成振荡器产生一个高频正弦波信号，当金属球下落过程中经过感应线圈使得线圈内的磁场发生变化，从而叠加到原有的正弦信号中，所得到的信号就是调幅信号通过金属感应线圈引出产生的一个高频磁场信号。D2在电路中起到整流的作用，然后经过RLC高频信号滤波，再经过Q2三极管所构成的放大电路进行信号放大，最后经过RC滤波后输出信号，D1的作用是防止振荡器对电源产生不利干扰，C1、C2对电源进行滤波。

2 理论分析

根据斯托克斯定律，光滑的金属球在无限广延的液体中运动时，当液体黏度较大，金属球半径很小且下落速度较小的条件下，金属球所受到的粘滞力为(即斯托克斯公式)[21]：

f=3πηdv

(1)

式中：d是金属球的直径；η是液体的粘度系数，Pa·s。

2.1 金属球在待测液体中下落时受力分析

金属球在待测粘性液体中下落时，同时受到3个铅直方向的力[22]如图4所示：金属球的重力G，液体作用于金属球的浮力F和金属球所受的粘滞阻力f(其方向与金属球运动方向相反)。其中重力表示为G=mg；浮力表示为F=ρgV0；粘滞力表示为f=3πηdv。

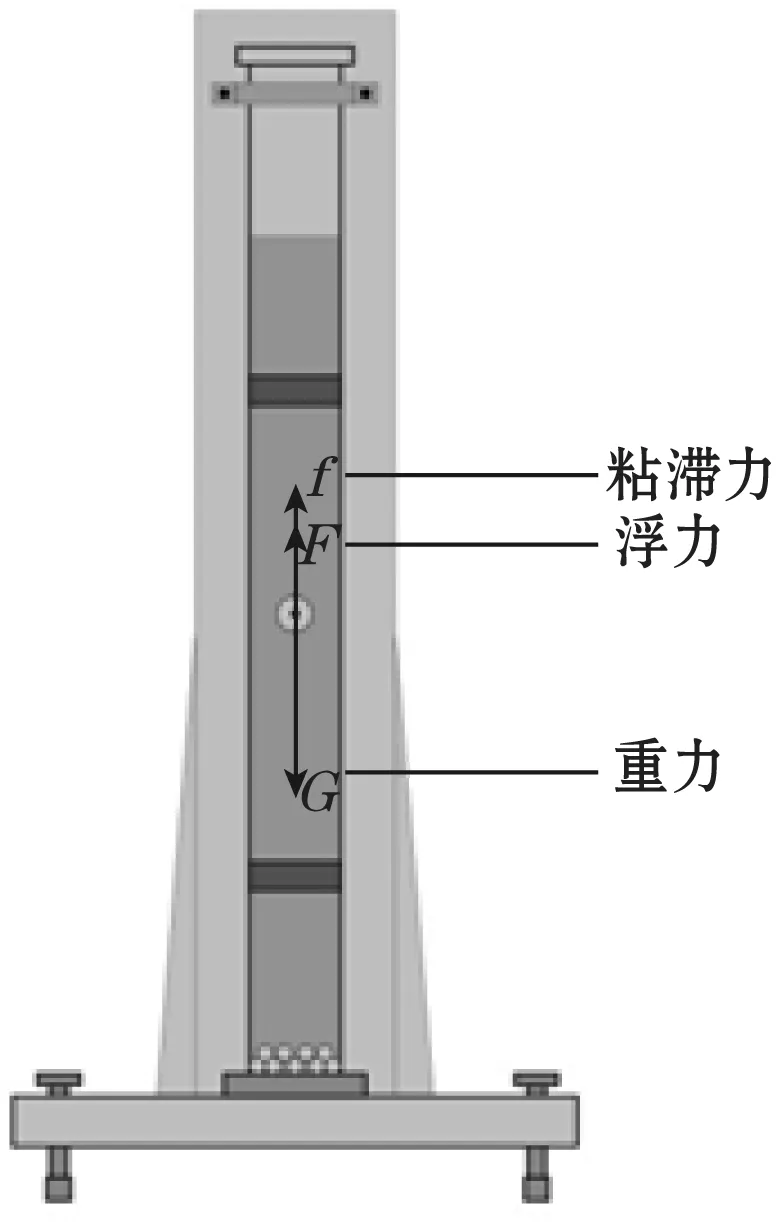
图4 受力分析图

2.2 大直径金属球变加速下落分析

待测液体中选用直径为D的大直径金属球进行测量，假设初速度和时间为0，随着小球下落速度不断增大，最终3个力未达到平衡，如图4所示，故金属球做变加速下落。表达式为

G>F+f

mg>ρgV0+3πηDv

(2)

假设大直径金属球变加速的加速度为a，则式(2)表示为

mg-ρgV0-3πηDv=ma

(3)

式中:m为小球质量；V0为小球体积；ρ为液体密度；D为金属球直径；η为液体黏度系数；v为小球速度；a为小球下落时的加速度。

(4)

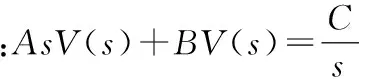
(5)

(6)

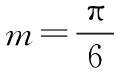
(7)

式中：v(t)为金属球加速下落速度；η为待测液体黏度系数；ρ0为小球密度；ρ为液体密度；D为金属球直径；t为大直径金属球加速下落的时间。

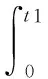
(8)

由式(8)可知：若测量出球下落的时间t和高度h，即能得到液体的粘度系数：

(9)

式中：h为量筒外壁两金属感应线圈之间的距离；P为常系数。

2.3 通用计算公式的推导与验证

根据斯托克斯定律可知，采用传统的落球法测量液体黏度系数时，认为当金属小球在待测粘性液体中下落时，由于开始速度尚小，阻力也不大，但随着下落速度增大，阻力也随之增大。最终使得金属球在待测液体中所受的3个力达到平衡。可表示为：G=F+f

mg=ρgV0+3πηDv

(10)

于是，小球作匀速直线运动，由上式可得：

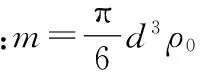
代入可得待测液体黏度系数η的计算式表示为

(11)

式中:ρ0为小球密度；h为小球匀速下落距离;t为小球下落h距离所用时间。

在实际实验测量中，由于待测液体应当盛在玻璃量筒中，因此难以满足斯托克斯定律中金属球在无限深广的液体中运动，所以假设金属球沿着量筒的中心轴线下落，应当将式(11)改动，以满足实际情况。

(12)

式中：φ为玻璃量筒的管径；l为待测液体在量筒中的高度。

本文根据大直径金属球在待测液体中实际运动情况，推导出了大直径金属球变加速直线运动的液体黏度系数η的理论公式(9)。

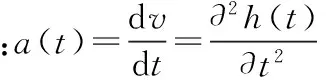
(13)

式中：η为待测液体的黏度系数；h量筒外壁上两金属感应线圈之间的距离；ρ0为小球密度；ρ是液体密度；D为大球的半径；K，P为常系数。

由式(12)、式(13)一致可得，采用大球变加速运动过程中推出的液体黏度系数η与下落时间t和下落距离h的函数关系式理论上正确。

3 实验研究

3.1 实验测量装置

采用金属感应式非接触测量法实验测量时，主要采用委托江苏慧硕科教仪器有限公司生产加工的实验装置，具体装置如图5所示。其中毫秒计的分辨率为1 ms，能够满足实验要求。通过对金属球直径大小的改变，能够有效减小相对误差，提高实验测量的精度。

图5 实验仪器装置

3.2 实验数据分析

采用上述实验装置在不同球径时分别进行多次实验，其中实验所用的金属球为市场上购买的不锈钢金属球，实验用待测溶液选用经典实验用的高纯度蓖麻油。实验后再对结果取平均值，实验数据如表1所示。

表1 蓖麻油实验球径大小与落球时间

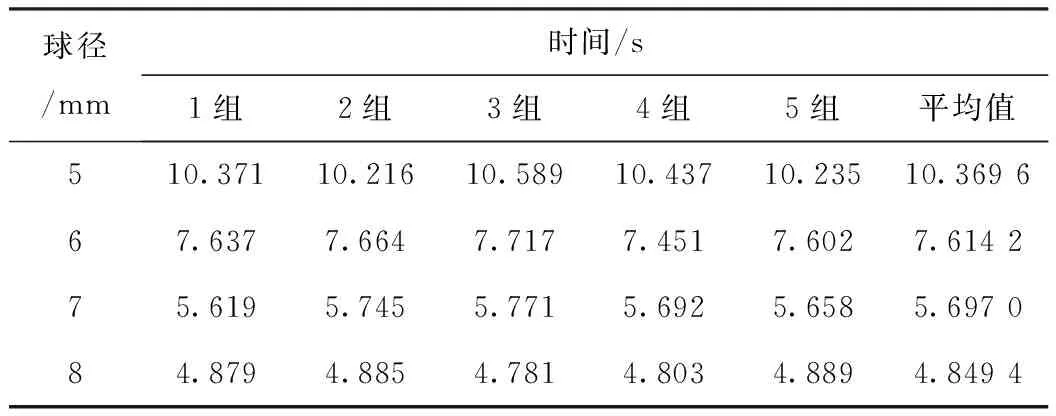
球径/mm时间/s1组2组3组4组5组平均值510.37110.21610.58910.43710.23510.369667.6377.6647.7177.4517.6027.614275.6195.7455.7715.6925.6585.697084.8794.8854.7814.8034.8894.8494

实验结果与理论计算结果对比如图6所示，其中理论计算采用本文中式(9)，在MATLAB7.1中进行仿真计算。实验结果与本文理论计算的误差如表2所示。

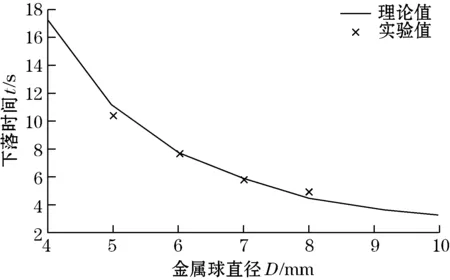
图6 金属球直径与下落时间的关系曲线

表2 实验数据误差分析

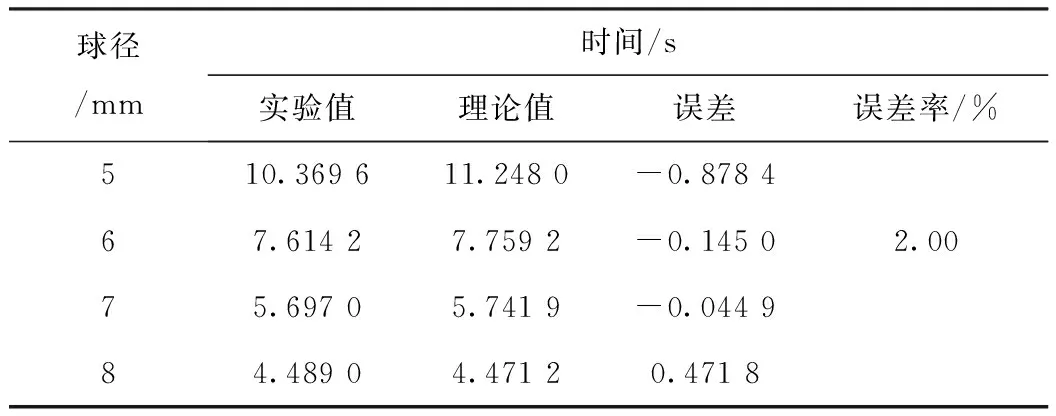
球径/mm时间/s实验值理论值误差误差率/%510.369611.2480-0.878467.61427.7592-0.14502.0075.69705.7419-0.044984.48904.47120.4718

3.3 实验结论总结

综上所述，针对本文所提出的液体黏度系数测量仪，通过理论和实验校正推导出采用大直径金属球的液体黏度系数通用计算公式为

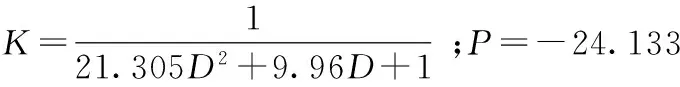
通过理论推导和实验验证可得，采用大直径非接触的金属感应式落球法对液体黏度系数进行测量能够有效降低相对误差，同时不受液体黏度和透明度大小的影响。

4 结束语

(1)本文基于电磁学原理中的电涡流效应，提出一种新型的金属感应式非接触液体黏度系数测量方法，解决了传统落球法中人为计时造成的误差问题，避免了因液体透明度大小对实验结果造成的影响。

(2)该方法以斯托克斯理论公式为基础，考虑了传统落球法中金属球直径大小对实验结果的影响，对大直径金属球在液体中下落过程进行受力分析，推导出大直径金属球下落的液体黏度系数计算通用公式，并运用Matlab对公式进行模拟计算。

(3)实验以蓖麻油为例，采用金属感应非接触测量方法对不同球径的金属球进行实验测量，结果表明测量误差不超过2%，验证了上述推导公式的合理性。

(4)推导出大直径金属球测量的通用公式，并通过实验证明了采用金属感应式落球法非接触测量液体黏度系数测量简单、快捷，且适用于不透明液体的粘度系数测量，精度较高。

[1] 代伟,兰小刚,徐平川,等.用落球法测液体黏度的实验条件分析.大学物理,2014,33(7):20-23.

[2] 刘东亮,董志国.落球式高粘性不透明流体粘度测量装置的设计.现代制造工程,2014(5):106-110.

[3] KUNDU P K,COHEN I M.FluidMechanices.Oxford:Elsevier,2008.

[4] 杨周琴,张朝霞.用落球法变温粘滞系数实验仪器测液体的粘滞系数误差分析.电子测量技术,2013,33(9):89-90.

[5] MAFFETTONE M, AFFTTONE P.Morphology estmiation from normal stress measurements for dilute immiscible polymerblends.RheologicaActa(S003524511),2003,42(1):158-165.

[6] MISHINARIK M. Flow behaviour of gellan gum aqueous solutions . Colloid and Polymer Sci2ence(S03032402X), 1999, 277(8): 727-734.

[7] 周超,梁良,魏诺.小球半径对落球法测液体黏度的影响.大学物理验,2002,15(2):6-11.

[8] 曹春梅,甄钊.落球法测液体粘滞系数实验的理论分析.物理与工程,2013,23(2):39-41.

[9] 周木,胡成华,史玲娜.液体粘滞系数测量仪器的研究.大学物理实验,2011,24(5):64-66.

[10] 巴合提古丽,阿斯利别克,张里荃,等.毛细管两端压强差对液体黏度测量的影响.大学物理实验,2011,24(6):12-13.

[11] 张潞英,陈国杰,周红仙,等.液体粘滞系数测量原理分析及仪器研制.实验科学与技术,2011,9(5):182-185.

[12] 刘文鹏,张庆李.粘度测量法进展.人工晶体学报,2007,36(2):381-384.

[13] 陈惠钊.粘度测量.北京:中国计量出版社,2002,56-140.

[14] 陈健,马奔,刘丽华,等.关于“落球法测量液体粘滞系数”实验的教学研究.实验室科学,2013,16(3):29-32.

[15] 刘鲍,闫赫,张宇,等.落球法测量液体粘滞系数实验的Matlab研究.东北电力大学学报,2013,33(3):87-90.

[16] 王玉清,任新成.落球法测液体黏度实验的改进.大学物理,2004,23(8):41-42.

[17] 濮兴庭,戚世瀚,王楠.落球法测定液体粘滞系数误差的研究.实验室科学.2014,17(1):22-24.

[18] 张海林,张爱军.CCD落球法液体黏度测定仪.实验技术与管理,2006,23(4):49-51.

[19] KITTA A,UMEL C.Measuring on-line and off-line noncontact ultrasound time of flight weld penetration depth.Welding Journal,2007,86(1):9-17.

[20] BANO M. A viscosity and density meter with a magnetically suspended rotor. Review of Scientific Instruments,2003,74(1): rials Science and Technology 2004 Conferenceon on Materials Damage Prognosis,New Orleans,Louisiana,2005:223-227.

[21] 马文蔚.物理学.北京：高等教育出版社，2008.

[22] 刘石劬.粘滞系数实验的误差修正及实验条件选择.实验科学与技术,2013,11(1):183-186.

Measurement of Liquid Viscosity Coefficient Based on Metal Induction Falling Ball Method

YANG Zhi-jun1, YIN Wen-qing1, LU Wei1, CAI Ting-ting2, ZHAO Xian-lin1

(1.College of Engineering / Key Laboratory of Intelligent Agricultural Equipment in Jiangsu Province,Nanjing Agricultural University, Nanjing 210031, China;2.Southeast University, Nanjing 210096,China)

Viscosity coefficient is one of the most important physical parameters of liquid. Respect to the shortcomings of adjusting, measuring and precision of the existing instruments that used in measuring viscous coefficients of liquids nowadays，a novel method to measure the falling time of a falling ball based on the metal induction principle to determinate the viscous coefficient of all kinds of liquids was presented. Firstly, the instrument for measuring liquid viscous coefficients in metal induction method was developed. Then the falling time of a metal ball was measured by means of it and the viscous coefficient of a liquid was worked out by existing formula. Furthermore, the formula of liquids viscous coefficients using larger balls was deduced in consideration of larger errors generated by small balls. Then the simulations and measuring experiments using metal balls of larger diameter were carried out and the data showed their good agreement. The experimental results show that the measurement accuracy of our instrument applying the proposed formula is not less than 98% with good repeatability.

viscous coefficient；metal induction；falling-ball method；non-contact measurement

张波波(1991—)，硕士研究生，主要研究方向为嵌入式系统应用。E-mail:zhangbo91@foxmail.com 李明伟(1957—)，教授，高工，主要研究方向为通信电子技术和智能仪器。E-mail: dlutcc@dlut.edu.cn

江苏省自然科学基金青年基金资助项目(BK20130696)；中央高校基本科研业务费专项资金资助项目(KYZ201427)

2014-12-23 收修改稿日期：2015-06-27

TP216.4

A

1002-1841(2015)10-0091-04