集成芯片式温度传感器MCP9700误差补偿方法

胡邦南,刘 琼

(湖南工业职业技术学院电气系，湖南长沙 410208)



集成芯片式温度传感器MCP9700误差补偿方法

胡邦南,刘 琼

(湖南工业职业技术学院电气系，湖南长沙 410208)

集成芯片式(IC)温度传感器MCP9800存在非线性误差，在高精度测温系统中需要进行误差补偿。提出了一种基于多项式拟合的集成芯片式温度传感器误差补偿方法：首先介绍了该传感器的测温原理；然后根据误差曲线低温和高温误差不一致且具有抛物线形状的特征，采用一阶和二阶误差补偿综合的方式，推导了传感器全量程的误差补偿公式。实验表明：这种补偿方式补偿效果好，实现容易，拓展了传感器的测温范围。

IC温度传感器；多项式拟合；二阶误差

0 引言

集成芯片式(IC)温度传感器具有灵敏度高、准确度高、体积小、电路接口方便、价格低廉、使用简单等优点，但这些传感器在极端高温和低温时精度会呈非线性下降，并且一般情况下这种非线性具有抛物线形状，因此在高精度的测温系统中必须进行误差补偿，以提高测量准确度。文献[1]采用硬件实现的两点温度补偿法，需要耗费硬件成本，且效果不理想；文献[2]采用插值法，需要测试很多个点的数据，且补偿效果一般；文献[3]提出了数字温度传感器的一种自适应动态补偿方法，解决了测温滞后性的问题，但没有进行测温误差补偿；文献[4]提出了一种基于预测模型的温度传感器动态补偿方法，改善了温度传感器动态响应特性，减少了测温滞后的时间，但同样没有进行测温误差补偿；文献[5]提出了一种基于径向基函数神经网络集成-模糊加权输出(RBFNNE-FWO)的数字温度传感器误差补偿方法，软件设计复杂，实现难度大。

本文根据IC温度传感器的测温原理，推导出描述IC温度传感器典型非线性特性的公式，利用单片机软件对公式进行计算，从而得到更精确的温度读数。

1 MCP9700测温原理

IC温度传感器使用完全导通的PNP晶体管来检测环境温度，其基极-发射极的结间压降具有与二极管相同的特性。这个结间压降与温度有关，可用来测量环境温度。式(1)显示了二极管正向电压VF和环境温度TA之间关系：

(1)

式中：K为波尔兹曼常数,K=1.380 7×10-23J/K；q为电子的电荷量,q=1.602×10-19C；TA为环境温度；IF为正向电流；IS为饱和电流。

IS是一个可变的常数，数值取决于晶体管的尺寸。恒定正向电流IF是用于偏置晶体管的，这样TA成为唯一的可变量。因为IS是会随工艺和温度的变化而显著变化，仅靠一个晶体管测量温度不可靠。

为了减少对于IS的依赖性，IC温度传感器采用两个晶体管来测量温度。若两个二极管分别采用恒定正向电流IF1和IF2进行偏置，同时两个电流比例因子为N(IF2/IF1=N)，则正向电压的差值(ΔVF)的推导过程如下：

ΔVF=VF2-VF1

(2)

(3)

ΔVF是一个不再依赖两个二极管的饱和电流，而是与绝对温度呈比例的电压信号。其斜率为：(86 μV/℃)· ln(N)|N=10= 200 μV/℃。对于模拟输出的IC温度传感器，将ΔVF放大后输出，对数字式温度传感器，将ΔVF放大后连至模数转换器输出。

在一定的温度范围内，ΔVF的精度取决于两个传感器上的IF和IS的匹配程度。在这两个参数中，任何一个参数不匹配，都会导致温度误差成非线性。

2 测温误差的多项式拟合方法

2.1 MCP9700误差特性曲线

在工作温度范围内，IC温度传感器具有典型的误差曲线。在高温和低温时，误差幅度呈指数增加，从而形成了抛物线形状的误差曲线。测试了50支MCP9700个器件，图1显示了其平均值和±1 ℃标准方差时的传感器精度曲线。

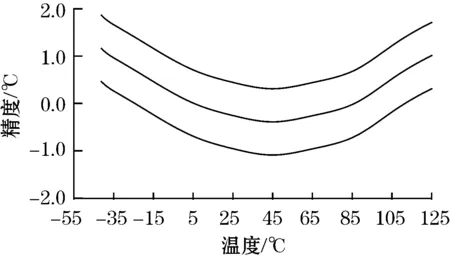
图1 MCP9700精度曲线

2.2 线性拟合

由图1看出，在-40～+125 ℃范围内，存在一阶误差斜率，或温度误差系数(EC1)。这个误差系数可以采用终端拟合方式进行计算,如式(4)：

(4)

式中：Thot为最高工作温度；Tcold为最低工作温度；ErrorT_hot为最高工作温度时的误差；ErrorT_cold为最低工作温度时的误差。

一旦计算出误差斜率，就能确定在低温时相应的偏移量，进而可调整低温时的误差，如式(5)所示：

ErrorT-1=EC1(TA-Tcold)+ErrorT_COLD

(5)

式中：ErrorT-1为一阶温度误差；TA为测试点温度。

显然，图1中Error-40取1.2，Error125取1.0，则EC1计算结果为-1.21×10-3。

2.3 多项式拟合

为了捕捉在图1中的抛物线形精度误差，需要计算二阶项及其相应系数。

在指定温度TA处通过指定计算出二阶误差ErrorT_2等于TA处的已知误差，从而计算得到式(6)中显示的二阶温度误差系数EC2。

ErrorT_2=EC2(Thot-TA)(TA-Tcold)+ErrorT_1

(6)

式中：ErrorT_2为二阶温度误差；EC2为二阶温度误差系数。

则通过变换式(6)而求解EC2，如式(7)所示：

(7)

例如，若取TA为+45 ℃，ErrorT_2等于+45 ℃ 时的温度误差-0.4 ℃，则得到EC2为-2.2×10-6℃-1。

式(7)显示当TA等于Thot或Tcold时，其二阶项强制为零，因此在一 阶误差项中没有增加任何误差。这是因为在Thot和Tcold极端温度处的误差已经包含在一 阶误差(ErrorT_1)中。式(8)为完整的可以用来补偿传感器误差的2 阶多项式。

ErrorT_2=EC2(Thot-TA)(TA-Tcold)+EC1(TA-Tcold)+ErrorT_cold

(8)

2.4 精度补偿

在使用IC温度传感器时，可应用下述多项式公式来补偿传感器误差，如式(9)所示：

Tcomp=Tsen-ErrorT_2|TA=Tsen

(9)

比如，若MCP9700 温度输出Tsen= +65 ℃，则补偿后的温度Tcomp为

Tcomp=65 ℃-ErrorT_2|TA=65 ℃=65 ℃-(-0.316 ℃)=65.316 ℃

图2显示了得到补偿后，MCP9700温度传感器的平均精度曲线。对于MCP9700，在整个工作温度范围内，传感器精度平均可提高到±0.05 ℃内。

图2 MCP9700 补偿后典型误差曲线

2.5 二阶温度系数EC2讨论

上面公式中的二阶温度补偿系数EC2是使用+45 ℃时的误差推导得到的，该温度点的补偿特性可以满足绝大多数场合的要求。但是通过改变推导EC2的温度点，可以在相对较窄的温度范围内得到更高的精度。

可以看出，比较0 ℃和45 ℃时的EC2数值，可以发现在低温时具有更高的精度。同样采用高于45 ℃时推导的EC2数值，在高温时具有更高的精度。但是精度误差变化的幅度并没有跟随EC2数值的变化而发生显著的变化。所以，采用45 ℃时的EC2数值可以得到相对实际的结果。

3 测试结果

将传感器MCP9700置于恒温槽，并且使用热电阻Pt100来精确测量温度，与传感器输出的温度值进行比较。测量结果见表1。

表1 测量精度 ℃

表1显示，使用公式补偿后，传感器精度极大提高了，且传感器的测温范围得到了拓展。

4 结束语

本文根据IC温度传感器具有抛物线形状的非线性误差曲线特征，构建了基于二阶多项式拟合的IC温度传感器误差补偿公式，利用这个公式来对传感器输出进行补偿。通过大量实验证明，采用这种方法补偿后的IC温度传感器的非线性误差大大减少，提高了测温准确度，这种补偿也拓展了传感器的温度测量使用范围；与其他方法相比，这种方法具有简便实用、性能最佳的特点。

[1] 蒋敏兰，胡生清，幸国全.AD590温度传感器的非线性补偿及应用.传感器技术,2001,20(10):54-56.

[2] 凌振宝，朱凯光，段清明.数字式温度传感器MAX6575 的非线性补偿设计.吉林大学学报,2003,21(3):227-230.

[3] 林海军，滕召胜，杨圣洁.数字温度传感器自适应动态补偿方法研究.仪器仪表学报，2009，30(1)：138-142.

[4] 程晓辉，郭松灵，赵洋.一种便携式多通道精密测温仪.航空计量技术，2000，20(5)：24-26.

[5] 林海军,滕召胜,杨进宝,等.基于RBF神经网络集成-模糊加权输出的数字温度传感器误差补偿.仪器仪表学报，2011，32(7)：1675-1680.

Error Compensation for IC Temperature Sensor MCP9700

HU Bang-nan，LIU Qiong

(Hunan Industry Polytechnic,Changsha 410208，China)

Nonlinear error compensation for integrated circuit temperature sensor MCP9800 is necessary in high accurate temperature measurement system.An error compensation method based on nonstationary polynomial fitting(NPF)was proposed.Firstly,the principle for measuring temperature was introduced.Secondly,according to the error curves in low temperature and high temperature were different and had parabolic shapes,the error compensation formulas were derived by the composition compensation of 1st order error and 2nd order error.Experiment results show that the method has good effects and is easy to realize,thus expanding the temperature measurement range of sensor.

integrated circuit temperature sensor;nonstationary polynomial fitting;2nd order error

湖南省科技厅科技支撑计划(2013GK3049)

2013-11-14 收修改稿日期：2014-12-02

TP212

A

1002-1841(2015)02-0094-02

胡邦南(1969—)，研究员级高工，主要研究方向为智能检测与嵌入式技术。E-mail：459475866@qq.com