高精度多声道超声波密度计

张兴红，邱 磊，陈 鑫，何 涛

(重庆理工大学，时栅传感及先进检测技术重庆市重点实验室，400054 重庆)



高精度多声道超声波密度计

张兴红，邱 磊，陈 鑫，何 涛

(重庆理工大学，时栅传感及先进检测技术重庆市重点实验室，400054 重庆)

当超声波在介质中传播时，其传播速度受介质密度的影响。基于此种特性，设计了一种高精度的超声波密度计。通过测量超声波在介质中的传播速度来间接实现被测介质密度的高精度测量。由于采用了高分辨率和高速度的信号采集电路以及数字细分算法，使超声波传播时间的测量达到ns级，为超声波密度计实现测量分辨率优于10 g/m3的高精度密度测量提供了保障。设计中采用分布式测头，将多对测头均匀布置在装有被测介质的容器外壁，使测得容器中被测介质的密度更加准确可靠。

超声波；分布式；密度测量；数字细分；高精度

0 引言

密度是表征物质特性的物理量之一，密度测量广泛地应用于现代国防、科技、工业、农业和日常生活等领域，是体现一个国家计量水平的重要方面[1]。 由于密度不能直接转换成电信号，必须先转换成浮力、压力、声速、相位、振动频率等，然后才能转换成电信号进行处理。这势必给密度的测量增加了很大的难度[2]。

工业上常用的液体密度计种类很多，有振动式液体密度计、电容式液体密度计、射线式液体密度计等。这些液体密度计在使用过程中都存在着一些不足之处，如：振动式和电容式成本低，在测量中应用较多，但测量准确度不高，维护较为麻烦；射线式可进行非接触的测量，但存在射线的辐射危害而较少被使用[3]。

近年来，随着高新技术的飞跃发展，提出了利用超声法测量液体密度的新思路[4]。用超声波来测量液体密度，其优点为实现了测量的非接触性和连续性，如果与控制系统连接，就可以随时控制液体的密度，使其保持一定的均匀性[5]。超声波式密度传感器可以实现非接触高精度密度动态测量，是一种有很好应用前景的密度传感器[6]。

1 超声波密度计的工作原理

利用超声波技术实现密度的测量是根据超声波在介质中传播时，其传播速度与介质的密度有关，当介质密度发生变化时，超声波传播速度也会发生改变。因此，可以通过测量超声波在介质中的传播速度来间接测量介质密度。式(1)为超声波的传播介质为液体时，传播速度与介质密度的关系式[7]：

(1)

式中：c为超声波在介质中的传播速度；ρ为介质的密度；k为介质的弹性模量。

超声波传播速度与传播时间的关系式为

(2)

式中：d为超声波的传播距离；t为传播时间。

由式(2)可得：当超声波传播距离一定时，只要测得超声波的传播时间就可以得出传播速度。

综合式(1)、式(2)可知，在传播距离一定时，只要测出超声波在介质中的传播时间就可以得出介质密度。

在设计中采用分布式测头，即将多对测头均匀安装在装有被测介质的容器外侧，让超声波穿过容器中的被测介质传播，实现超声波在每对测头之间的发射和接收。图1为3对测头的安装示意图。

测头的核心部分是压电超声换能器，它可以把具有一定能量的模拟电压信号转换为机械振动从而发出超声波，也可以将由超声波产生的机械振动转换为模拟电压信号[8]。图中3对换能器(E11与E21、E12与E22、E13与E23)分别相对安装在装有被测介质的容器外壁上，其位置要低于被测介质的高度，以便于超声波穿过被测介质。

超声波驱动信号激励换能器E11、E12、E13发射超声波，对应的换能器E21、E22、E23将接收到的超声波信号转换成电信号，再利用数字细分插补算法进行数据的分析处理，得到多个密度值，最后对这几个密度值求平均得到最终的密度值。

2 超声波密度计的结构组成

超声波密度计原理框图如图2所示。该密度计主要由超声波发射换能器组(E11、E12、E13)、超声波接收换能器组(E21、E22、E23)、中央处理单元CPU、现场可编程门阵列FPGA、A/D转换电路、放大电路、滤波电路、功率放大电路、D/A转换电路、通道切换电路、显示电路和键盘电路等构成。3对超声波换能器(E11与E21、E12与E22、E13与E23)两两相对安装在装有被测介质的容器外壁上。

图2 超声波密度计原理框图

中央处理单元CPU向FPGA发出开始采样命令后，FPGA启动对超声波发射换能器的驱动和对超声波接收换能器输出信号的采样。由FPGA产生的数字信号经过D/A转换电路转换为模拟信号，再经功率放大电路放大后，通过通道切换电路的通道切换后逐个轮流加载在超声波发射换能器组中的一个换能器上，使其发出超声波信号。超声波接收换能器组中的换能器输出的电信号经过滤波电路滤波后，经过运算放大电路放大后连接到A/D转换电路。

A/D转换电路将接收到的信号转换成数字信号，并把数据逐一存入构建于FPGA内的RAM存储区中。CPU根据对存储在FPGA中的数据进行处理，计算出超声波在两两相对安装的换能器之间的传输时间，进而就可确定一个密度值。

通道切换电路进行通道切换使得超声波驱动电路得以驱动超声波发射换能器组中的其他换能器，并完成超声波信号的发射和接收，得到新的密度值。最后CPU对这几个密度值求平均就能得出最后的密度值。

3 超声波驱动信号及回波信号

超声波驱动电路主要包括中央处理单元CPU、现场可编程门阵列FPGA、数模转换器D/A和功率放大电路。超声波驱动电路的主要功能是产生超声波驱动信号激励超声波换能器发射超声波。超声波驱动信号是由中央处理器CPU控制下的现场可编程门阵列FPGA产生的数字正弦波经过D/A转换，再经过放大滤波电路而成的模拟正弦波。超声波驱动信号为连续的8个频率为1 MHz的正弦波构成。其中超声波驱动信号的频率及周期数是通过综合分析得出的。超声波驱动信号与换能器发射的超声波信号的频率相同。当超声波信号的频率越高时，超声波传播时间的测量分辨率越高，但是超声波的传播距离越短，因此对驱动信号的选择应合理。超声波驱动信号的示意图如图3所示。

图3 超声波驱动信号示意图

超声波回波信号处理电路包括滤波电路、放大电路、A/D转换电路、现场可编程门阵列FPGA、中央处理单元CPU.其功能是对换能器接收的回波信号进行处理，并算出超声波的传播时间。超声波回波信号与超声波驱动信号相对应，其频率也为1 MHz。超声波回波信号的幅值会随着驱动信号的连续增加而不断增大，但是其幅值增大到足够大时不再增大。为保证对传播时间的精密测量，将驱动信号的周期数设为8个。当驱动信号停止时换能器依然会产生回波信号，但是其幅值逐渐减小，直到最后幅值为零。因此超声波回波信号会随着驱动信号的发射和停止呈现出幅值先增大后减小的周期性变化，如图4所示。其中回波信号中幅值最大的波形为特征波，特征波的过零点为特征点。

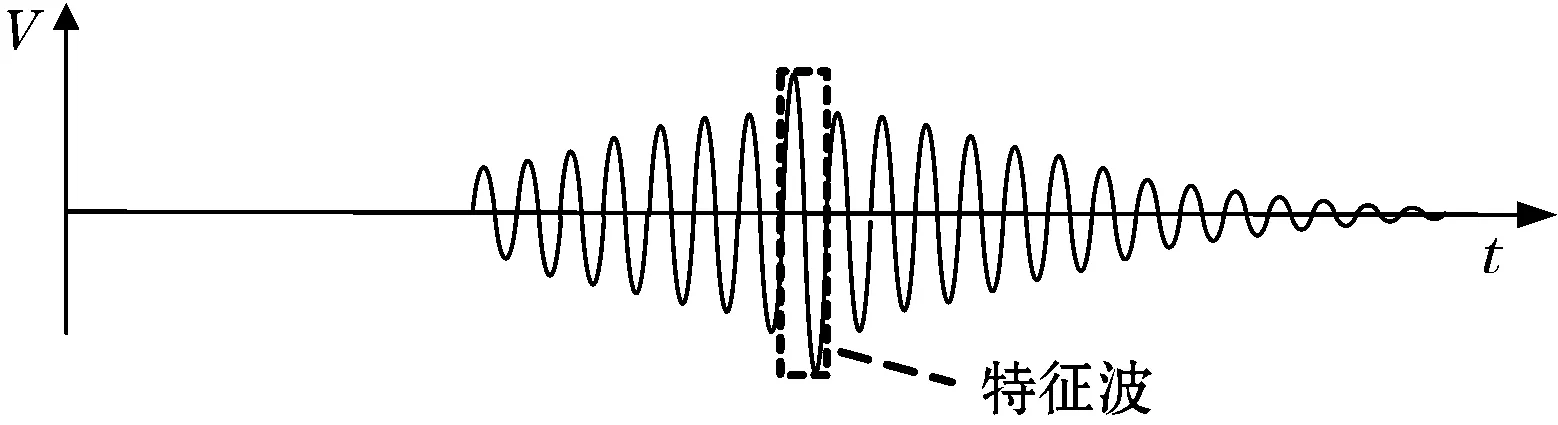
图4 超声波回波信号示意图

4 传播时间的精密测量

利用超声波技术测量介质密度是通过测超声波在介质中的传播速度来实现。当传播距离一定时，测出超声波的传播时间就能得出传播速度，即只要测出超声波的传播时间就能测出介质的密度。因此，实现超声波传播时间的高精度测量是保证介质密度精密测量的关键。

在超声波测密度过程中，超声波的传播时间就是换能器A发射的超声波信号上的任意一点与换能器B接到的回波信号上相对应的那一点之间的时间间隔[9]。只要确定超声波传播时间的起点与终点就能得出超声波的传播时间。又超声波传播时间的起点是由硬件精确确定，所以超声波传播时间的精密测量的关键是确定传播时间的终点，其精度依赖于终点的精确确定[10]。将超声波传播时间的起点时刻设为第八个周期信号的过零点，则超声波传播时间的终点就是特征波上的过零点，即特征点。超声波传播时间的示意图如图5所示，点P0就是特征点。

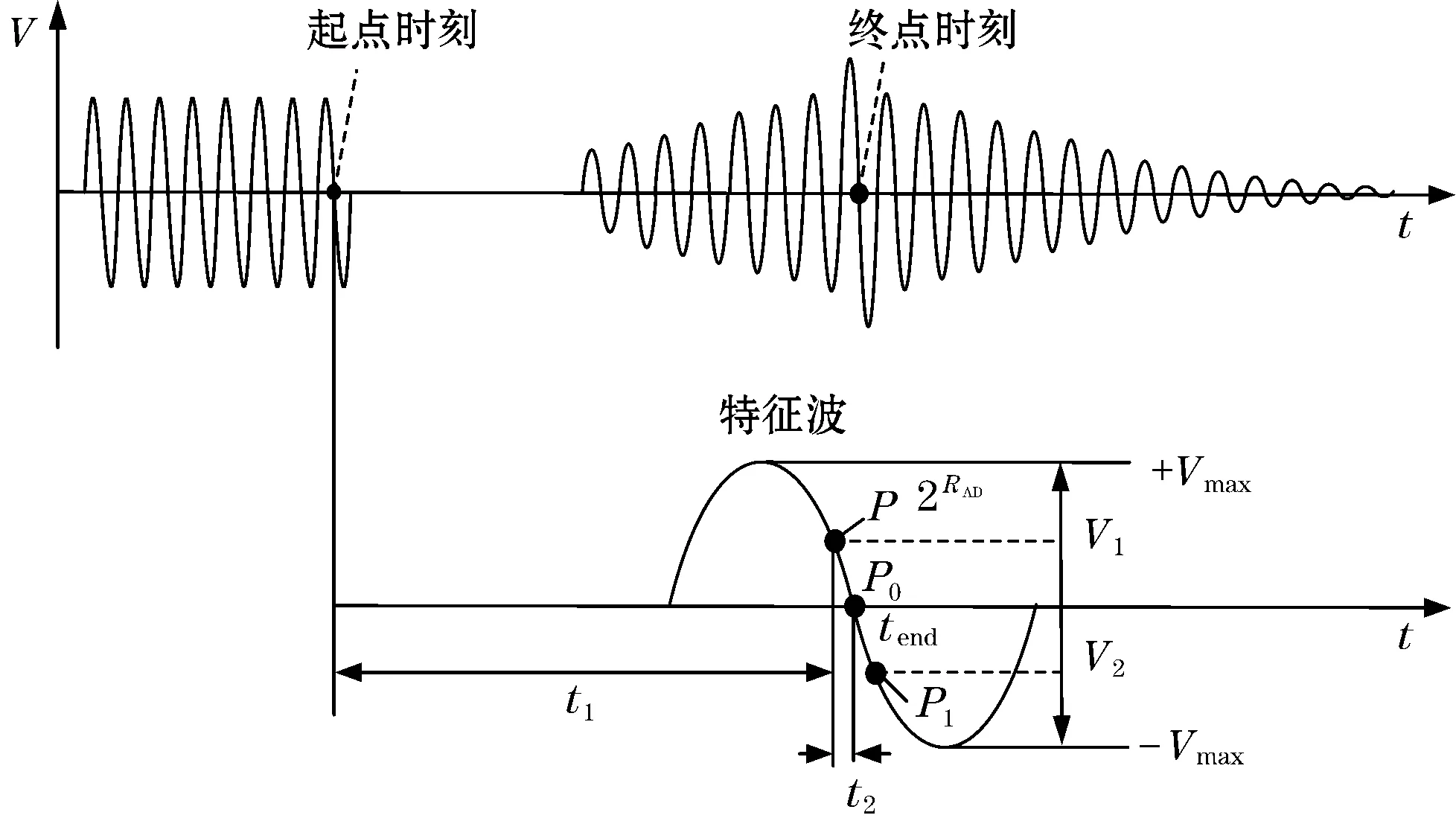
图5 超声波传播时间的示意图

超声波传播时间的终点时刻是通过采用数字细分插补算法来对A/D采样的数据进行处理来精确确定的。运用数字细分插补算法的前提是找到特征波，并确定特征点P0附近的两个点P和P1。当对A/D采样点的值逐点比较，找出采样点的最大值就可以很容易地确定幅值最大的波形(特征波)，在特征波的采样点中存在两个相邻的点，其幅值一个大于零一个小于零，幅值大于零的点为P，幅值小于零的点就为P1。以采样点P和P1两点对应的时刻作为基准，用数字细分插补算法可以准确计算出过零点P0所对应的时刻。其具体方法如下：

设A/D的采样频率为fA/D，相邻两个采样点之间的时间即采样周期为tA/D；从第一个采样点到采样点P之间的采样数为N，采样点P对应的采样值为V1，采样点P所对应的时刻为t1；采样点P1对应的采样值为V2；采样点P与过零点P0之间的时间为t2，过零点P0对应的时刻为tend，超声波传播时间的起点时刻为tstart超声波的传输时间为t，则：

(3)

(4)

在过零点附近较小的区域内，正弦波的波形接近于直线，可以根据直线插补的方法确定t2：

(5)

则过零点所对应的时刻，即超声波传输时间终点所对应的时刻为

(6)

超声波的传输时间为

(7)

5 密度测量的分辨率分析

从式(5)可知，超声波传输时间终点所对应时刻的分辨率为

(8)

设超声波回波信号的频率为1 MHz；A/D的分辨率是10位，采样频率为16 MHz，那么可以将信号的幅值分为1 024份，同时在正弦波正的最大值到负的最大值的半个周期内最多可以采8个点。则将正弦波正的最大值到负的最大值的半个周期内的波形看作是直线，可知：

(9)

而正弦波从正的最大值到负的最大值的半个周期内的过零点附近曲线的斜率远大于峰值附近曲线的斜率，则：

|V2-V1|>128

(10)

(11)

由于超声波传输时间起点所对应的时刻可以精确确定，则超声波传输时间测量的分辨率取决于超声波传输时间终点所对应时刻的分辨率[11]，故超声波传输时间测量的分辨率小于0.488 ns。安装在容器外壁上多对换能器E11与E21、E12与E22、E13与E23之间的距离均是固定的，测得超声波在一定温度下在换能器E11与E21、E12与E22、E13与E23之间的传播时间，就可以计算出3个与之相对应密度值，对这3个密度值求平均得到的结果就是最终的密度值。

例如，25 ℃时水的密度为997.0 kg /m3，乙醇的密度为789.0 kg /m3，25 ℃时，超声波在水中的传播速度是1 497 m/s，在乙醇中的的传播速度是1 207 m/s。如果超声波的传输距离是0.3 m，则在25 ℃时，超声波的在水中传输时间是2.004 0×10-4s，在乙醇中的传输时间是2.485 5×10-4s，在两种介质中，超声波的传输时间差为4.814 9×10-5s，两种介质的密度差为208.0 kg/m3。当超声波传输时间的分辨率优于4.814 9×10-9s，则可以实现分辨率优于21 g/m3的密度测量，设计的超声波密度计可以实现0.488 ns的时间测量，则超声波密度计对密度测量的分辨率可达10 g/m3。

6 结束语

针对现有的常规密度计所存在的不足之处，运用新的思路设计了超声波密度计，该密度计具有以下2个特点：

(1)采用分布式结构设计，将多对测头均匀布置在装有被测对象容器外壁的各个方位，由此获取多个位置的密度值，取其平均值，这样得出的结果更接近真实值。

(2)数字细分插补算法和A/D转换电路保证了对超声波传播时间的精密测量，基于FPGA的硬件电路使得数据能被快速处理，使密度测量具有很好的实时性。

经分析，设计的超声波密度计可以实现分辨率优于0.488 ns的超声波传播时间的测量，使超声波密度计的测量分辨率能达到10 g/m3。

[1] 徐泽清，吴东艳，张立.谐振式液体密度传感器研究.黑龙江工程学院学报(自然科学版)，2009，23(4)：28-61.

[2] 王海峰，熊刚，赵小凯.基于超声波特性的油品密度仪设计.声学技术，2007，26(5)：887-890.

[3] 姚明林，陈先中，张争.超声波液体密度传感器.传感器技术，2005，24(5)：57-60.

[4] 唐得刚，冯新泸，罗平亚，等.一种新型超声波油料密度检测装置的设计.传感器技术，2005，24(9)：63-64 .

[5] 陈先中，姚明林，张争.智能化超声波液体密度计.仪表技术与传感器，2005(8)：15-16.

[6] 张欲晓，樊尚春.液体密度传感器.计测技术，2006，26(1)：1-3.

[7] 曹凤国.超声加工技术.北京：化学工业出版社，2004.

[8] 蔡伟，刘淑香，向凤云，等.基于FPGA的高精度超声波温度计设计.电子技术应用，2011，37(8)：10-12.

[9] 张兴红，张慧，陈锡侯，等.一种精密测量超声波传输时间的方法.北京理工大学学报，2011，31(6)：717-721.

[10] 张兴红，向凤云，张天恒，等.超声波传输时间精密测量方法及应用研究.中国机械工程，2012，23(6)：651-654.

[11] 张兴红，蔡伟，向凤云，等.精密超声波温度测量仪设计.仪表技术与传感器，2011(6)：32-35.

Design of High-precision Multi-channel Ultrasonic Densimeter

ZHANG Xing-hong，QIU Lei，CHEN Xin，HE Tao

(Chongqing Key Laboratory of Time-grating Sensing and Advanced Testing Technology，Chongqing University of Technology，Chongqing 400054，China)

The propagation speed of ultrasonic wave is affected by the medium’s density when propagating in the medium. A high accuracy multi-channel densimeter was designed on the basis of this characteristic. The high accuracy measurement of the measured medium’s density was realized indirectly by measuring the propagation speed of ultrasonic wave. The high resolution and fast signal collection circuit and the digital subdivision algorithms made the measurement of the ultrasonic wave propagation time reach nanoseconds, making sure that the ultrasonic densimeter can realize high-precision density measurement with the resolution better than 10 g/m3. In the design, the measuring probes were distributed. Several couples of measuring probes were uniformly placed on the outer wall of vessel which was contained with the measured medium, and this design was conducive to make the measurement results more accurate and reliable.

ultrasonic wave;distributed;density measurements;digital subdivision;high accuracy

国家自然科学基金资助项目(51275551)；重庆市自然科学基金资助项目(cstc2012jjA70004，cstc2012jjA40062)

2014-01-08 收修改稿日期：2014-10-21

TP216

A

1002-1841(2015)02-0020-03

张兴红(1970—)，教授，博士，主要研究方向为计算机辅助测试技术。