一种基于混合参数和DSm T的证据网络多连通结构推理方法
郭 强,关 欣,潘丽娜,孙贵东
(1.海军航空工程学院信息融合研究所,山东烟台 264001;2.海军航空工程学院电子信息工程系,山东烟台 264001;3.海军航空工程学院基础部,山东烟台 264001)
一种基于混合参数和DSm T的证据网络多连通结构推理方法
郭 强1,关 欣2,潘丽娜3,孙贵东2
(1.海军航空工程学院信息融合研究所,山东烟台 264001;2.海军航空工程学院电子信息工程系,山东烟台 264001;3.海军航空工程学院基础部,山东烟台 264001)
针对现有的证据网络推理模型无法进行复杂的多连通知识网络结构下的信度推理问题,提出一种基于混合参数和DSmT的证据网络推理方法,将条件信度函数和联合信度函数同时作为多连通证据网络的结点备选参数,并根据多连通网络结构的结点特点进行选择,并提出DSmT的证据网络信度合成方法,不仅可以有效地进行复杂多连通图结构的证据网络信度推理,并可有效解决证据网络的不确定性高冲突信息融合问题。最后通过典型的胸腔诊断问题实例,验证了本文方法的有效性。
证据网络;信息融合;信度合成;证据推理;Dezert-Smarandache Theory
0 引 言
为了解决多源异类知识框架下的不确定性信息融合、推理问题,基于网络模型的知识表示和不确定推理方法得到了广泛的研究[1,2]。贝叶斯网络(BN)[3]作为贝叶斯理论与图论相结合的不确定性知识处理方法,将不确定性先验知识以先验概率和条件概率的形式进行表示并形成有向无环图的网络知识结构,对证据信息进行不确定性推理,该方法在故障诊断、专家系统、评估预测、军事系统等领域都得到了广泛的应用[4-10]。但是贝叶斯网络只能处理符合贝叶斯信度的精确证据,且无法区分不知道和不确定的知识,对不确定性推理带来了一定的局限。价值网络(VN)[11]作为一种综合多种不确定知识表示方法的理论框架,提出了将证据理论与图论相结合处理不确定性知识的方法。该方法通过边缘化和组合两种手段,对不同知识框架下的信息进行转换和融合,取得了很好的效果[12]。但是该方法的价值评价以不同框架的笛卡尔乘积的联合信度函数为基础,对于复杂的网络模型,需要很大的存储空间和运算量,推理效率较低。Xu Hong和 Smets[13]最早提出了证据网络的概念,首次将知识网络结构中变量之间的关系用条件信度函数取代联合信度函数进行表示,相比价值网络推理,简化了不确定性推理的复杂度。近年来,Boutheina Ben Yaghlane等人致力于基于条件信度函数的证据网络理论的研究[14,15],并提出了基于二进制树的证据网络推理方法。
通过对证据网络的研究发现,现阶段证据网络的研究存在两个问题,一是对于复杂的多连通知识结构,现有的证据网络模型无法进行有效的推理,二是对于证据网络结点信度推理过程中如何有效解决高冲突的不确定性信息合成问题。本文针对多连通证据网络知识结构结点的特点,对结点参数的类型进行选择,提出了一种基于条件、联合信度混合参数的证据网络模型结构,并首次将DSmT理论应用于证据网络推理中,提出一种基于DSMT的证据网络信度合成方法,对网络结点的不确定性冲突信息进行合理的融合,更有效地进行整个证据网络的信度推理。最后通过的典型的胸腔医学诊断问题实例,验证了本文方法的有效性。
1 理论基础
1.1 乘积空间下的信度函数理论
对乘积空间的信度理论研究,需要定义两个基本的运算:扩展和边际化。
定义1 设X定义在识别框架ΘX上,Y定义在识别框架ΘY上,那么从ΘX到ΘX×ΘY的空扩展是一个定义在ΘX×ΘY上信度函数,其基本信度分配为

定义2 设X定义在识别框架ΘX上,Y定义在识别框架ΘY上,belX(x|y)是在给定y⊆ΘY时,ΘX上的条件信度函数,那么belX(x|y)在ΘX×ΘY上B扩展的得到的信度函数belX×Y定义为
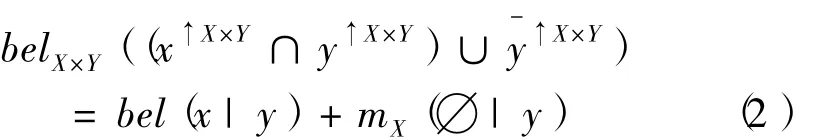
B扩展得到的基本信度分配函数定义为
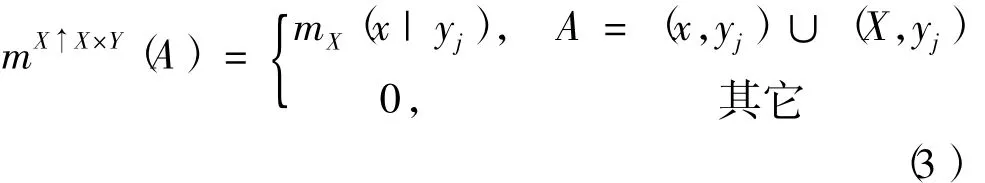
定义3 设X定义在识别框架ΘX上,Y定义在识别框架ΘY上,X的证据mX和Y的证据mY的合取定义在ΘX×ΘY上,

定义4 设m是X上的基本信度分配,Y⊆X,Y≠∅,m对Y的边际化表示为m↓Y

1.2 证据网络以及GBT和DRC理论
证据网络是一种有向无环图模型,如图1所示。由代表变量的结点和连接这些结点的有向边、以及相应的关系参数构成,是图论与证据理论的结合。每个结点代表一个变量,一般是研究问题的抽象;结点间有向边的集合,表示结点之间的因果关系或影响关系。
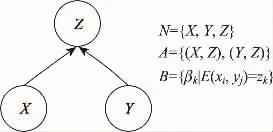
图1 基本的证据网络模型
Smets[16]提出了 GBT理论 (the generalized Bayesian theorem)和DRC准则(the disjunctive rule of combination)作为基于条件信度函数的证据网络正向推理和反向推理的重要工具。
定理2 对于任意xi∈ΘX和yi∈ΘY,基于GBT理论,条件信度函数belX(x)|y可按下式计算


定理3 对于任意xi∈ΘX和yi∈ΘY,基于DRC准则,条件信度函数belY(y)|x可按下式计算

1.3 DSm T理论
定义3 (DSmT融合规则[17])在DSmT的框架下,超幂集DU在并运算和交运算中是封闭的。定义一个基本概率赋值函数,即m(·):DU→[0,1],给定的混合DSm模型相关的多个证据源(A∈DΘ)则有如下DSmT组合规则:

2 证据网络推理模型
证据网络的推理方法,实质上就是在给定的证据网络结构、参数和已知的证据下,通过扩展和边缘化、条件信度转换以及信度合成公式,计算网络结构中任意其他结点事件发生的信度[15]。根据网络的拓扑结构的不同,证据网络精确推理方法也分为基于单连通图结构的推理方法和基于多连通图结构的精确推理方法。
2.1 基于单连通图结构的证据网络推理模型
设U为证据网络模型中一个有限个结点的集合,对于每一个结点X∈U,其父结点用Pa(X)表示,子结点用Ch(X)表示。在每一个结点X存储一个先验信度BelX0,同时存储它与父节点之间的条件信度函数{BelXY:Y∈Pa(X)},当有一个结点得到一个观测证据时,该结点的信度就会被更新,并向其父结点传递消息(用λ值表示),向其子结点传递消息(用π值表示)。证据网络单连通图结构如图2所示。基于单连通图结构推理方法,应用基于PolyTree的消息传递算法。这种算法基于每个结点上局部出现的信息进行计算,也称为局部算法。

2 证据网络单连通图结构
2.2 基于多连通图的证据网络推理模型
大部分情况下,证据网络结构都是一个有向无环图,而不仅仅是一棵树。这就意味着在图结构中至少有两个结点通过两条路径以上进行连接。这种网络结构就是多连通图网络结构,它常发生在一些变量通过多个因果机制影响其他变量的情况下。对此情况,PloyTree算法是无效的。因为如果两个结点通过多条路径连接,其中一个结点的观测证据信息通过多条路径传递给另外一个结点时就会存在重复计算。我们参考经典的胸腔诊断问题给出证据网络多连通图结构如图3所示。一个医生必须判断一个抱怨自己有呼吸短促症状的病人是得了以下哪一种病:支气管炎、肺癌和肺结核。医生的医学知识被总结如下:呼吸短促(D)可能是由于肺结核(T)和肺癌(L)两者之一(E)和支气管炎(B)造成的。近期对亚洲的访问(A)有可能会增加肺结核的几率,抽烟(S)一般会导致肺癌(L)和支气管炎(B)。一份单独的X光检查(X)不能区分肺结核和肺癌之一哪一个。如图所示,结点(D)和结点(S)之间形成两条多连通的通道,即形成了S L E D和SB D。若这两个结点有观测证据信息,基于单连通图结构的消息传递算法就会失效。

图3 胸腔诊断证据网络多连通图结构
Boutheina Ben Yaghlane采用联合信度函数参数下的证据网络递归的构建方法得到基于二进制连接树结构,然后将树结构中所有的联合信度结点转换为条件信度函数结点,如图4所示。
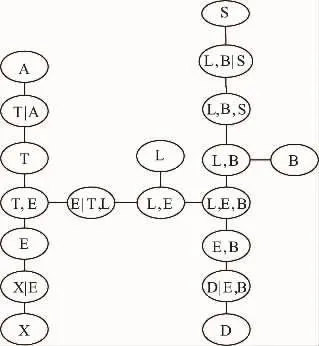
图4 基于二进制树结构的条件信度函数证据网络结构
3 一种基于混合参数的证据网络建模方法
对证据网络推理模型进行分析可知:
1)在单连通推理模型上,所有的关系结点选用条件信度函数可以有效的减少存储空间和计算量,此时不需要使用联合信度函数进行推理;
2)在多连通推理模型上,当将所有的关系结点全部转换为条件信度函数时,在某些结点会出现无法计算的问题,例如图4中,结点E|T,L接收m(E,L)或m(T,E)时,无法有效利用m(E|T,L)进行空间的转换,因为(E,L)或(T,E)之间存在着联系,分别是因果的关系中的因和果的部分。这时使用条件信度无法进行有效推理,需采用联合信度函数参数,将(E,L)或(T,E)分别扩展到(T,E,L)中,再在该空间下进行融合。
由以上对现有的证据网络推理模型的分析可知,证据网络结构模型的参数类型不能仅包含联合信度函数或是条件信度函数,应根据多连通知识网络结构的结点特点选择结点的参数类型,基于此提出一种基于条件信度和联合信度函数混合参数的证据网络多连通结构推理模型,参数的选择遵循以下规律:
1)对于关系结点的某个相邻结点只有单变量时,选择条件信度函数参数;
2)对于关系结点的某个相邻结点是变量集合,且变量同为某因果关系的因或果时,选择条件信度函数参数;
3)对于关系结点的某个相邻结点是变量集合,且变量各为某因果关系的因和果中的部分时,选择联合信度函数参数。
本研究对胸腔网络诊断模型的证据网络推理结构按照以上规律进行网络参数选择,得到的基于混合参数的证据网络多连通结构推理模型模型如图5所示。比较本研究提出的证据网络推理结构和图4中的推理结构,本研究推理结构在保证最小融合存储空间和运算量的基础上,解决了部分结点依据条件信度参数无法有效推理融合的问题,如图4中的结点E|T,L。

图5 基于混合参数的证据网络推理结构
4 基于DSm T的证据网络信度合成方法
不同框架下的信息通过证据网络结构转换或扩展到同一个框架下,就要进行信度合成,现有的证据网络模型结构的信度合成方法仍然采用传统的证据理论(DST),此时如果证据信息是不确定的和高度冲突的,那么会导致错误的结果,而如果网络中某一结点的信息是错误的,那么会间接导致整个网络模型推理的瘫痪。
而证据网络的结点信度合成经常是在低维空间扩展到高维空间上进行信度合成的,某一维度的冲突都会更容易导致DST无法有效进行信度合成,本文根据分析认为证据网络模型中应采取DSmT作为证据网络的信度合成方法。
考虑某结点接收相邻结点传来的信息为m1(1,1,1)=0.9,m1(1,2,1)=0.1,该结点本身存储的证据网络联合信度函数参数为m2(1,1,2)=0.1,m2(1,2,1)=0.9。通过DST进行该结点信度合成过程见表1,通过DSmT进行该结点进行合成过程见表2。

表1 通过DST进行信度合成的过程

表2 通过DSm T进行信度合成的过程
假设结点的变量均存在排斥性假设,即证据源的联合信度函数和传来的证据之间对信息的描述是一致的,不存在模糊的交集,则DSmT的超幂集空间转化为shafer模型的幂集空间。得到的基于DSt进行信度合成和基于DSmT进行信度合成的结果比较见表3。

表3 基于DSt和DSm T进行信度合成结果的比较
从表3可知,基于DSt的信度合成方法将冲突进行了归一化,得到了错误的结果(分析可知,第二个变量为1或2的可能性都很大,无法判断),而且信度值为1,绝对的错误结果会对整个网络推理的结果带来巨大的影响;而基于DSmT的信度合成方法对矛盾的冲突证据信息进行了有效的融合,得到了满意的结果,更有利于整个证据网络的推理。
5 实例分析
下面利用典型的胸腔诊断问题进行实例分析,来验此方法的有效性。胸腔诊断证据网络多连通证据网络结构如图3所示,提出的基于混合参数和DSmT证据网络多连通推理结构如图4所示。假设,通过先验知识得到各结点参数如下:
D|EB条件信度参数为
m(D=是|(E=是,B=是),(E=是,B=否),(E=否,B=是))=0.9,
m(D=否|(E=是,B=是),(E=是,B=否),(E=否,B=是))=0.1,
m(D=是|(E=是,B=是),(E=否,B=是),(E=否,B=否))=0.7,
m(D=否|(E=是,B=是),(E=否,B=是),(E=否,B=否))=0.3,
m(D=是|(E=是,B=是),(E=是,B=否),(E=否,B=否))=0.7,
m(D=否|(E=是,B=是),(E=是,B=否),(E=否,B=否))=0.3,
m(D=是|(E=是,B=否),(E=否,B=是),(E=否,B=否))=0.7,
m(D=否|(E=是,B=否),(E=否,B=是),(E=否,B=否))=0.3.
L,B|S条件信度参数为
m(L=是,B=是|S=是)=0.3,
m(L=是,B=是|S=否)=0.1,
m(L=是,B=否|S=是)=0.4,
m(L=是,B=否|S=否)=0.1,
m(L=否,B=是|S=是)=0.2,
m(L=否,B=是|S=否)=0.1,
m(L=否,B=否|S=是)=0.1,
m(L=否,B=否|S=否)=0.7.
T|A条件信度参数为
m(T=是|A=是)=0.7,
m(T=是|A=否)=0.2,
m(T=否|A=是)=0.3,
m(T=否|A=否)=0.8.
X|E条件信度参数为
m(E=是|X=是)=0.9,
m(E=是|X=否)=0.1,
m(E=否|X=是)=0.1,
m(E=否|X=否)=0.9.
TLE联合信度参数为
m(T=是,L=否,E=是)=0.3,
m(T=否,L=是,E=是)=0.4,
m(T=否,L=是,E=否)=0.1,
m(T=是,L=否,E=否)=0.2.
依据如下信息进行推理:假设患者患有呼吸短促现象明显即m(D=是)=1,近期未去过亚洲即m(A=是)=0,m(A=否)=1,医生初步判断患者可能是支气管炎m(B=是)=0.8,m(B=否)=0.2,经过X光照射患者患有肺结核或肺癌即m(E=是)=1,m(E=否)=0。明显医生的初步判断和X光诊断是冲突的证据。推理结构如图4,步骤如下:
1)由病症现象信息m(D=是)=1,
根据D|EB条件信度参数反向推理得
m(E=否,B=否)=0.1,
m(E=是,B=否)=0.3,
m(E=否,B=是)=0.3,
m(E=是,B=是)=0.3.
2)扩展到LEB结点,因为无参数,所以为空扩展,即
m(L=Θ,E=否,B=否)=0.1,
m(L=Θ,E=是,B=否)=0.3,
m(L=Θ,E=否,B=是)=0.3,
m(L=Θ,E=是,B=是)=0.3.
3)由于有医生的初步诊断信息m(B=是)=0.8,m(B=否)=0.2,经过传递到LB结点再传递到LEB结点,均为空扩展,为
m(L=Θ,E=Θ,B=是)=0.8,
m(L=Θ,E=Θ,B=否)=0.2
4)此时,医生的初步诊断信息与客观证据信息同时在LEB结点,故进行DSmT融合运算,m(L=Θ,E=否,B=Θ)=0.08,m(L=Θ,E=是,B=Θ)=0.24,
m(L=Θ,E=否,B=是)=0.24,
m(L=Θ,E=是,B=是)=0.24,
m(L=Θ,E=否,B=否)=0.02,
m(L=Θ,E=是,B=否)=0.06,
m(L=Θ,E=否,B=是)=0.06,
m(L=Θ,E=是,B=是)=0.06.
组合乘积得
m(L=Θ,E=否,B=Θ)=0.08,
m(L=Θ,E=是,B=Θ)=0.24,
m(L=Θ,E=否,B=是)=0.3,
m(L=Θ,E=是,B=是)=0.3,
m(L=Θ,E=否,B=否)=0.02,
m(L=Θ,E=是,B=否)=0.06.
5)证据信息m(A=是)=0,m(A=否)=1经过T|A结点,由正向推理得到
m(T=是)=0.2,m(T=否)=0.8.
6)证据信息m(E=是)=1,m(E=否)=0与T|A结点信息经过空扩展在TE结点融合并空扩展到TLE结点得,
m(T=是,E=是,L=Θ)=0.2,
m(T=否,E=是,L=Θ)=0.8.
7)在TLE结点处与联合信度参数
m(T=是,L=否,E=是)=0.3,
m(T=否,L=是,E=是)=0.4,
m(T=否,L=是,E=否)=0.1,
m(T=是,L=否,E=否)=0.2.
进行DSmT融合得,
m(T=是,L=否,E=是)=0.06,
m(T=Θ,L=是,E=是)=0.08,
m(T=是,L=是,E=Θ)=0.02,
m(T=Θ,L=否,E=Θ)=0.04,
m(T=Θ,L=否,E=是)=0.24,
m(T=否,L=是,E=是)=0.32,
m(T=否,L=是,E=Θ)=0.08,
m(T=Θ,L=否,E=Θ)=0.16.
由于再无其他结点含有T的信息,故在此结点处组合乘积得到变量T的信度为
m(T=是)=0.08,m(T=否)=0.4,
m(T=Θ)=0.52
8)此时,将TLE结点中的信息边缘化得到LE的信息并空扩展传到LEB结点,得到
m(L=否,E=是,B=Θ)=0.3,
m(L=是,E=是,B=Θ)=0.4,
m(L=是,E=Θ,B=Θ)=0.1,
m(L=否,E=Θ,B=Θ)=0.2.
9)与4)得到的LEB结点信息进行DSmT融合运算如下,
m(L=否,E=Θ,B=Θ)=0.024,
m(L=否,E=是,B=Θ)=0.072,
m(L=否,E=Θ,B=是)=0.09,
m(L=否,E=是,B=是)=0.09,
m(L=否,E=Θ,B=否)=0.006,
m((L=否,E=是,B=否)=0.018,
m(L=是,E=Θ,B=Θ)=0.032,
m(L=是,E=是,B=Θ)=0.096,
m(L=是,E=Θ,B=是)=0.12,
m(L=是,E=是,B=是)=0.12,
m(L=是,E=Θ,B=否)=0.008,
m(L=是,E=是,B=否)=0.024,
m(L=是,E=否,B=Θ)=0.008,
m(L=是,E=是,B=Θ)=0.024,
m(L=是,E=否,B=是)=0.03,
m(L=是,E=是,B=是)=0.03,
m(L=是,E=否,B=否)=0.002,
m(L=是,E=是,B=否)=0.006,
m(L=否,E=否,B=Θ)=0.016,
m(L=否,E=是,B=Θ)=0.048,
m(L=否,E=否,B=是)=0.06,
m(L=否,E=是,B=是)=0.06,
m(L=否,E=否,B=否)=0.004,
m(L=否,E=是,B=否)=0.012.
最后组合乘积得:
m(L=否,E=Θ,B=Θ)=0.024,
m(L=否,E=是,B=Θ)=0.12,
m(L=否,E=Θ,B=是)=0.09,
m(L=否,E=是,B=是)=0.15,
m(L=否,E=Θ,B=否)=0.006,
m(L=否,E=是,B=否)=0.03,
m(L=是,E=Θ,B=Θ)=0.032,
m(L=是,E=是,B=Θ)=0.12,
m(L=是,E=Θ,B=是)=0.12,
m(L=是,E=是,B=是)=0.15,
m(L=是,E=Θ,B=否)=0.008,
m(L=是,E=是,B=否)=0.03,
m(L=是,E=否,B=Θ)=0.008,
m(L=是,E=否,B=是)=0.03,
m(L=是,E=否,B=否)=0.002,
m(L=否,E=否,B=Θ)=0.016,
m(L=否,E=否,B=是)=0.06,
m(L=否,E=否,B=否)=0.004.
10)LEB的运算结果经过边缘化到相邻的单变量结点,得到以下结果
m(L=是)=0.5,m(L=否)=0.5,
m(E=是)=0.6,m(E=否)=0.12,
m(E=Θ)=0.28,
m(B=是)=0.6,m(B=否)=0.08,
m(B=Θ)=0.32.
结合7)中T结点得到的单变量信度结果,得到最后的所有单变量的信度结果。
m(T=是)=0.08,m(T=否)=0.4,
m(T=Θ)=0.52.
经过经典Pignistic变换[18]得到决策结果为
P(L=是)=0.5,P(L=否)=0.5,
P(E=是)=0.74,P(E=否)=0.26,
P(B=是)=0.76,m(B=否)=0.24,
P(T=是)=0.34,m(T=否)=0.66.
由以上结果进行分析:
1)对医生的诊断,即患者可能患有支气管炎B的可能性经过推理得出了(0.6,0.08,0.32)的信度结果,虽然较医生的诊断,不确定性增多,但P(B=是)=0.76,对B的支持度很高。
2)对X光照射得到的结果,即患者患有肺结核或肺癌的可能性经过推理得出了(0.6,0.12,0.28)的信度结果,对于X光照射的绝对肯定的诊断结果有了非常大的修正,P(E=是)=0.74,对E的支持度较高,但略低于医生的诊断结果。
3)进一步分析X光照射得到的结果,由于肺结核(T)和肺癌(L)两者之一都可能造成E,具体判断患者是得了T还是L,还要经过其他证据信息进行融合推理,分别得出了(0.08,0.4,0.52)和(0.5,0.5,0)的信度结果和P(T=是)=0.34,P(L=是)=0.5的决策结果,从结果可知,本文方法对肺结核(T)的可能性支持度很低,而对于患者患有肺癌(L)的支持度也是模棱两可的,仍较高的支持医生的患者患有支气管炎B的诊断。
由此可知,所提出的基于混合参数和DSmT的证据网络推理方法处理上述胸腔典型的诊断问题,对于X光诊断和医生的诊断结果发生高冲突的情况下,仍可以有效推理出合理的结果,根据推理结果较高的支持医生的诊断,患者可能患有支气管炎B的可能性更大,而最不可能患有肺结核T,也有一定的可能患有肺癌,这样的结果足以指导医生去做更有效的检查,排除肺癌的可能。基于混合参数和DSmT的证据网络推理方法,依据多连通网络结构选取适合的结点参数,保证了推理的有效进行,并由于尽量利用条件信度函数推理减少利用联合信度函数进行推理,有效地减少了计算量,减小了存储空间,提高了推理效率。
6 结 语
研究对现有的证据网络模型无法有效进行复杂多连通知识结构推理的问题,提出了一种基于条件、联合信度函数的混合参数的证据网络模型结构,该结构依据知识网络结构结点的特点选择适合推理的结点参数进行建模,并将DSmT引入结点信度合成中,提出一种基于DSmT的证据网络信度合成方法,对网络结点的不确定性高冲突信息合理的融合,可以更有效地进行证据网络推理。本文最后通过典型的胸腔诊断案例,验证了基于混合参数和DSmT的证据网络推理方法的有效性和优越性。
[1]SHAFER G,SHENOY P P,MELLOULIK.Propagating belief functions in qualitative Markov trees[J].International Journal of Approximate Reasoning,1987,(1):349-400.
[2]MELLOULIK,SHENOY P.Qualitative Markov Networks[C].Bouchon B,Yager R R(eds.).Uncertainty in Knowledge-Based Systems.Springer-Verlag Berl in Heidelberg,1987:69-74.
[3]PEARL J.Probabilistic Reasoning in Intelligent Systems:Network of Plausible Inference[M].San Mateo,CA:Morgan Kaufmann,Inc.,1988.
[4]WEBER P,MEDINA-OLIVA G,et al.Overview on Bayesian Networks Applications for Dependability,Risk Analysis and Maintenance Areas[J].Engineering Application of Artificial Intelligence,2010.
[5]王双成.贝叶斯网络学习、推理与应用[M].上海:立信会计出版社,2010.
[6]张连文,郭海鹏.贝叶斯网引论[M].北京:科学出版社,2006.
[7]黄友平.贝叶斯网络研究[D].北京:中国科学院计算技术研究所,2005.
[8]孙兆林.基于贝叶斯网络的态势估计方法研究[D].长沙:国防科学技术大学,2005.
[9]郭百钢.基于Bayes网络的项目投资风险评估与决策方法研究[D].南京:南京理工大学,2004.
[10]李海军等.贝叶斯网络理论在装备故障诊断中的应用[M].北京:国防工业出版社,2009.
[11]SHENOY P P.Valuation-Based Systems:A Framework for Managing Uncertainty in Expert Systems[C].Zadeh L A,Kacprzyk J(eds.).Fuzzy logic for the Management of Uncertainty.John Wiley& Sons,NewYork,1992:83-104.
[12]SHENOY PP.Binary Join Trees for Computing Marginals in the Shenoy-Shafer Architecture[J].International Journal of Approximate Reasoning,1997,17:239-263.
[13]Xu H,Smets P.Reasoning in Evidential Networks with Conditional Belief Functions[J].International Journal of Approximate Reasoning,1996(14):155-185.
[14]YAGHLANE B B,SMETSP,MELLOULIK.Directed Evidential Networks with Conditional Belief Functions[C].Nielsen TD,Zhang N L.(Eds.).Proceedings of ECSQARU-2003,LNAI 2711,Springer-Verlag,2003,291-305.
[15]YAGHLANE B B,MELLOULIK.Inference in Directed Evidential Networks Based on the Transferable Belief Model[J].International Journal of Approximate Reasoning,2008(48):399-418.
[16]Ph.Smets.Belief fuctions:The Disjuctive Rule of Combination and the Generalized Bayesian Theorem[J].International Journal of Approximate Reasoning,1993,9:1-35.
[17]FLORENTIN S,JEAN D.黄心汉,李新德(译). DSmt理论及其在信息融合中的应用(文集)[M].北京:国防工业出版社,2011.
[18]SMETSP.Data Fusion in the Transferable Belief Model[C].Proc.of 3rd Int.Conf.on Inf.Fusion,Fusion 2000,pp.PS21-PS33,Paris,France,July 10-13,2000.

郭 强(1986—),男,博士研究生,主要研究方向为信息融合、异类源知识融合研究;
E-mail:gq19860209@163.com
关 欣(1978—),女,辽宁人,博士,教授,主要研究方向为多源信息融合、电子对抗等;
潘丽娜(1964—),女,吉林人,本科,教授,主要研究方向为物理学、红外与光电传感器应用;
孙贵东(1989—),硕士研究生,主要研究方向为信息融合、目标识别等研究。
An Inference M ethod for Evidential Networks of M ultip ly Connected Structure Based on M ixed Parameters and DSm T Theory
GUO Qiang1,GUAN Xin2,PAN Li-na3,SUN Gui-dong2
(1.Research Institute of Information Fusion,Naval Aeronautical and Astronautical University,Shandong Yantai264001,China;2.Electronics and Information Department,Naval Aeronautical And Astronautical University,Shandong Yantai264001,China;3.Department of Basic Science,Naval Aeronautical And Astronautical University,Shandong Yantai264001,China)
Aiming at the problem that the exited evidetial networks are not able to perform efficient inference in themulti-connected knowledge network model,an inferencemethod for evidetial networks is proposed based on mixed parameters and DSmT theory.The conditional belief funtion and joint belief function are both contained in the parameters and DSmT theory is applied in tht evident fusion method.It resolves the problem ofmulti-connected networks and fuses the uncertain and highly conflict evident information.Finally,the effectiveness of themethod is tsetified by the inference of the classic chest clinic problem.
evidential networks;information fusion;evidential inference;belief fusion;Dezert-Smarandache Theory
TP212.9
:A
:1673-5692(2015)01-067-08
10.3969/j.issn.1673-5692.2015.01.011
2014-10-16
2014-11-22
教育部新世纪优秀人才支持计划(NCET-11-0872)

