总功率受限下的双向多中继系统功率分配方案

王 林，芮国胜，张 洋

（1.海军航空工程学院研究生管理大队，山东烟台 264001；2.海军航空工程学院（空场）电子信息工程系，山东烟台 264001）

总功率受限下的双向多中继系统功率分配方案

王 林1，芮国胜2，张 洋2

（1.海军航空工程学院研究生管理大队，山东烟台 264001；2.海军航空工程学院（空场）电子信息工程系，山东烟台 264001）

针对放大转发双向多中继协同通信系统，提出了一种基于最大化最小双向速率准则的功率分配方案。将功率分配问题分解为用户节点功率分配和中继节点功率分配两部分，首先通过将多中继节点信道等效为单中继节点信道，简化了用户节点功率分配，然后应用矩阵变换实现了分布式的中继节点功率分配，减少了反馈开销，降低了计算复杂度。仿真结果表明，提出的功率分配方案在系统双向可达速率和误码率两方面指标均优于现有双向中继功率分配策略，而且性能增益随着中继数目的增加而提升。

协同通信；放大转发；双向多中继；功率分配

0 引 言

中继协同通信技术通过多个用户间彼此共享天线，形成虚拟的MIMO信道，可以显著提升信道容量，获得分集复用增益，并且能够扩展无线通信系统的覆盖范围［1-4］。然而，目前协同通信系统大都基于单向传输信道，实际通信中系统需要4个时隙才能完成整个通信过程，这就使频谱效率受到较大的损失，为此，放大转发（AF，Amplify-and-Forward）和解码转发（DF，Decode-and-Forward）协议下的双向中继机制受到关注［5］，随后文献［6］推导了双向中继系统的容量取值界，证明了双向中继比单向中继系统有更高的频谱效率。

在协同通信系统中，合理的功率分配对提升中继信道的性能和资源利用率具有重要作用［7］。功率分配在单向协同系统中的研究较为充分，文献［8］针对总发射功率恒定的多中继系统，提出一种单向放大转发通信系统最优功率分配方案，并且推导了理论表达式。双向中继通信系统的功率分配研究目前主要集中在单中继的三节点模型，文献［9］提出了满足总功率受限条件下，使双向通信链路的中断概率最小的功率分配算法。文献［10］针对不对称双向中继信道条件下功率分配和中继选择进行研究。文献［11］对多天线情况下的单中继三节点模型进行了研究，根据最小和均方误差（MSMSE）准则，以较小的复杂度得到了MSE最优的中继处理矩阵的闭合表达式。对于双向多中继的协同通信系统，由于两用户节点及所有中继节点的总功率都受到限制，所以功率分配的复杂度很高，目前研究涉及较少。

针对双向多中继通信网络，提出了一种优化功率分配算法，在瑞利衰落信道环境下，通过功率优化分配使双向较小传输速率的信道速率最大化，该方法中继节点仅需要已知本地信道状态信息（CSI），占用反馈资源少，计算复杂度低，提高了系统的双向信道容量。文中的符号表示如下：（·）*为取对象元素的共轭，（·）T为矩阵或向量的转置，（·）H为矩阵或向量的共轭转置，‖·‖F为向量的F范数，diag（x）为以x的元素依次作为对角元的对角矩阵。

1 系统模型

双向多中继通信系统传输模型由两用户节点Ui（i＝1，2）和n个中继节点Ri（i＝1，2，……，n）组成。如图1所示，所有的节点单元均配置单天线且工作在半双工模式下，中继节点（R1，R2，……，Rn）通过AF模式为两个用户节点U1与U2互相交换信息，所有信道均为独立同分布的慢衰落Rayleigh信道，且根据信道的互易性，从节点U1到中继节点Ri和中继节点Ri到U1的信道增益相同设为gi，从节点U2到中继节点Ri和中继节点Ri到U2的信道增益相同设为hi。两用户节点的发射功率分别为Pi（i＝1，2），中继节点Ri的发射功率pi。两用户节点U1和U2已知所有信道的信道参数，中继节点Ri已知其前后相邻信道的信道增益gi与hi。

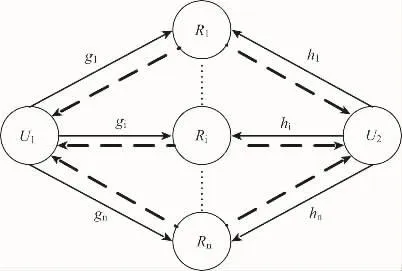
图1 双向多中继系统模型

假设整个系统中所有中继节点以及用户节点之间是严格同步的，完成双向中继通信过程需要2个时隙。在第1个时隙内，2个用户信源同时向所有中继广播各自的同频信息s1与s2，第i个中继节点Ri的接收信号为

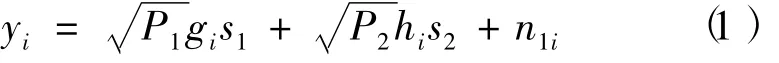
其中，n1i为中继Ri上的零均值单位方差加性白高斯噪声。在第2个时隙中，经过多个中继节点对信息进行放大转发，每个中继Ri的放大增益可表示为wi，则发送的信号为

式中，wi定义为第i个中继的功率分配因子，是功率分配算法需要设计的参数。其受限于中继Ri前后条链路的信道统计信息获得的增益［12］，wi与节点发射功率pi的关系可表示为

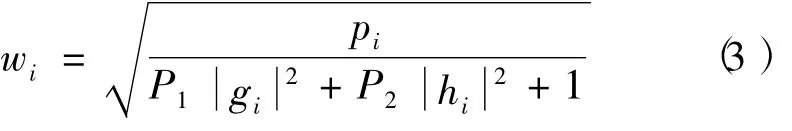
在第2个时隙内，每个中继Ri把处理后的信号广播给2个用户。由于信道是准静态慢衰落，可假设信道在连续2个时隙内保持不变［3］。用户U1接收到的信息可表示为

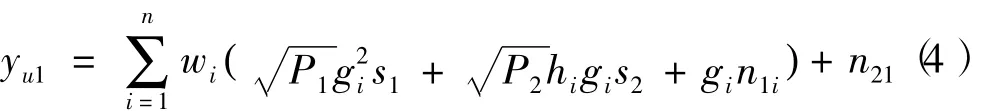
同理，用户U2接收到的信息可表示为

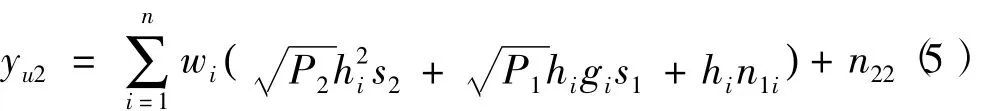
式中，n21、n22分别为第2个时隙内，两用户节点U1与U2上的零均值单位方差加性白高斯噪声。

上面两式中的第一项分别是每个用户节点自己的发送信号经过信道又到达原始发送端，这对有用信号造成干扰，因而称之为“自干扰”，由于U1与U2已知各自相邻链路的估计信道和发送信息，根据自干扰消除［13］可以得到

根据上式可以得到两条链路的接收信噪比，通过接收信噪比可进一步得到用户U1到U2的传输速率R12，以及用户U2到U1的传输速率R21，其表达式为

本研究的目标是在所有节点总功率固定的条件下，通过数学推导优化得到所有用户及中继节点功率分配参数，进而最大化系统的双向信道可达传输速率。

2 功率分配方案

在通信系统中，功率是十分有限的资源。在功率资源有限的前提条件下，如何通过有效的功率分配算法来提高系统的整体性能是一个十分重要的问题。针对整个系统的双向信道较小传输速率最大化的目标，设计出用户节点发射功率Pi及中继节点的功率分配因子wi，其中，wi通过各个中继节点分布式计算可避免传统的集中式处理方式的弊端，更加适合工程实现。

基于式（9）中的双向信道可达传输速率，通过求解下面的优化问题可以得到最优的双向中继功率分配方案

上式为一个非凸函数多变量优化的问题，很难求解。可将其分为两部分求解，分别对用户节点和中继节点进行功率分配。

2.1 用户节点功率分配

首先假定各中继节点功率相同，只对两用户节点进行功率分配，可将多个中继节点的信道系数等效为单中继节点的信道系数，即，w为中继放大增益。中继节点的等效功率以pR表示。根据文献［14］可知，为实现单中继双向较小可达传输速率最大化，需使双向信道传输速率相等，即R12＝R21，否则假设R12＞R21，则P2可以减小，则总功率可继续减小，与总功率限制矛盾。所以根据式（8）和式（9）可得

且由式（3）可得

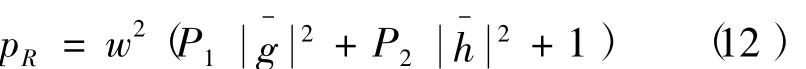
由式（10）可知，在高信噪比时当R12和R21取最大时有

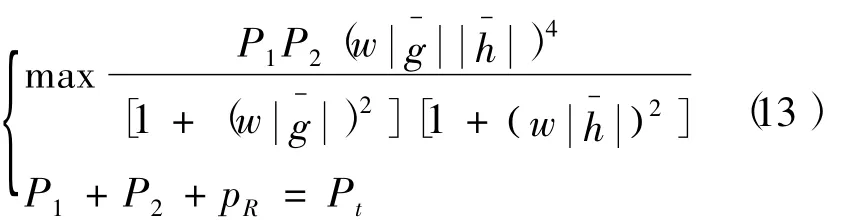
通过联立以上3式，可得用户节点的优化分配功率为

由式（14）和式（15）可知用户节点功率占用了总功率的一半，其余功率可在多个中继节点之间进行分配。

2.2 中继节点功率分配

由于所有中继节点将分配总功率的一半，式（10）的优化问题可转化为中继节点功率分配的子优化问题

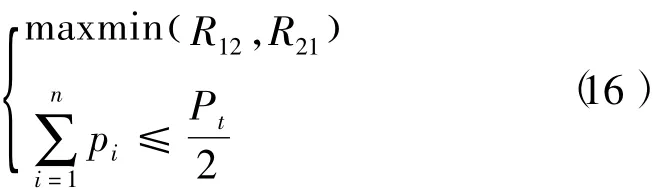
由2.1节可知，当双向速率相等，且中继节点总功率达到最大时，双向较小传输速率才能达到最大。所以上式可变为

针对上述问题可以应用矩阵变换方法求解上述最大化问题，将上式进行等价变换，并表示成矩阵形式如下

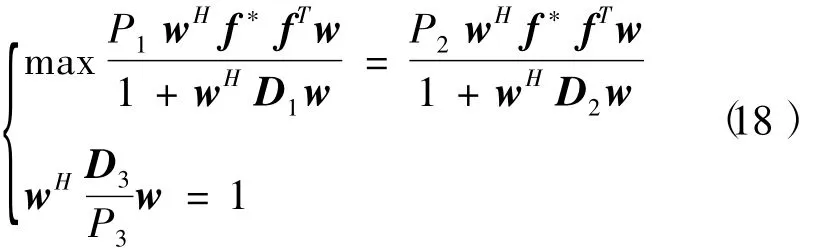
显然，问题（18）的最大化问题等效于下面的最小化问题。

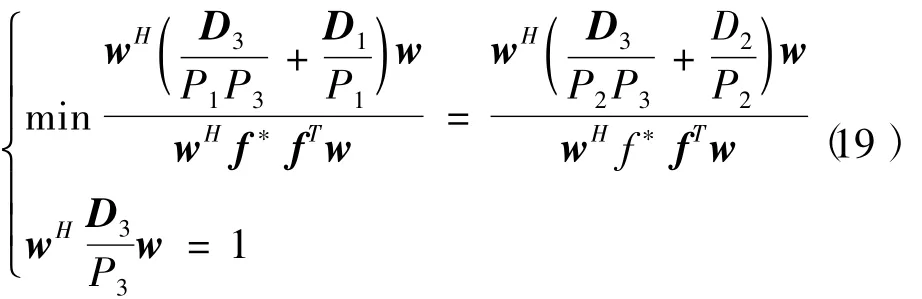
对上式所给出的约束条件放宽，将上式第一行等式左右两端相等的两项和变为新的目标函数，并令q＝，可得下式

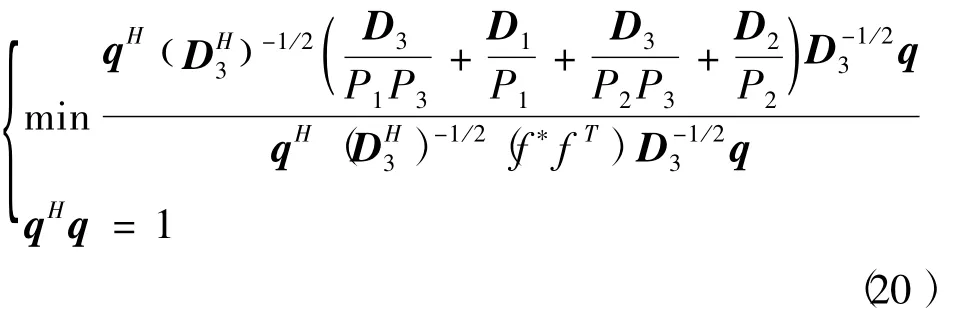
上式为一种约束最小化问题，可以通过约束下的广义奇异值分解求得唯一解［14］，其等效于下面的最大化问题

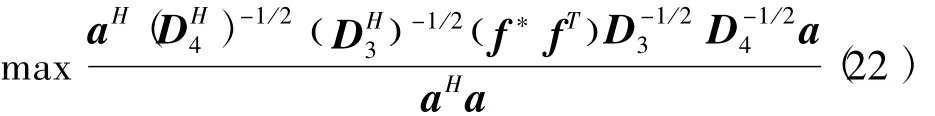
由此可进一步得到

上述问题的最优解为

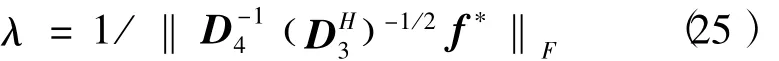
由式（24）可以得出w的最终表达式

这里λ为归一化因子，目的是调整发射功率的大小，用来满足式（20）中的约束条件，其表达式可以表示如下

则功率分配因子可表示为

从上式可以得出，求得每个中继的功率分配因子wi只由其前后相邻的信道增益信息gi与hi确定，而不需要已知其他中继与信源之间的信道增益。归一化因子λ可以由任意一个用户节点通过计算后广播给每个中继［15］。

2.3 方案步骤总结

（1）获取系统初始信息：通过系统反馈得到信道增益参数，其中户节点U1和U2需要获取所有信道的信道参数，中继节点Ri仅需获取其前后相邻信道的信道增益gi与hi，并设置双向中继协同通信系统总功率阈值Pt。

（2）用户节点功率分配：对于给定的总功率阈值Pt，通过等效多中继信道为单中继信道的方法，计算式（14）和式（15）求得两用户节点的发射功率Pi（i＝1，2）。

（3）计算归一化因子λ：选择任意一个用户节点，根据已经得到的用户功率，通过式（25）对归一化因子λ计算，并对所有中继节点广播计算所得数值。

（4）计算功率分配因子wi：各个中继利用得到的用户节点功率归一化因子λ，并且已知其前后相邻的信道增益信息gi与hi，通过式（27）分布式计算得到分配因子wi，整个系统功率分配完成。

3 仿真结果及性能分析

本节以最大可达速率以及误比特率性能为指标，通过蒙特卡洛仿真来验证上节提出的优化功率分配对系统性能的影响。式（8）和式（9）为系统最大可达速率的表达式，并采用BPSK调制方式。在仿真中，将噪声方差设置为1。所有信道都为瑞利平坦衰落信道。

为了说明所提选择算法的优越性，下面将其与以下2种功率分配方案方案进行比较：文献［8］提出的联合中继选择和功率分配方案；等功率分配方案，即分配给各个节点相等的功率。分别比较不同发射总功率限制下，系统可达速率及误码率两项指标。并在不同中继数目下分析了3种方案的系统可达速率性能。

当中继数目为5时，3种功率分配方法的系统可达总速率随系统总功率阈值Pt的变化曲线如图2所示。由图可知，本研究所提功率分配方案相比等功率分配方案和文献［8］方案，可明显提高系统可达总速率性能。以总功率等于15 dBw时为例，在本研究所提的功率分配方案下，系统可达总速率为2.5 bit／s／Hz；而在文献［8］方案和等功率分配方案下，系统可达总速率分别为1.7 bit／s／Hz和1.5 bit／s／Hz。相对其他两种方案，本研究所提方案的系统可达总速率有50%左右的提升。随着功率的增大，提升幅度还进一步增大。

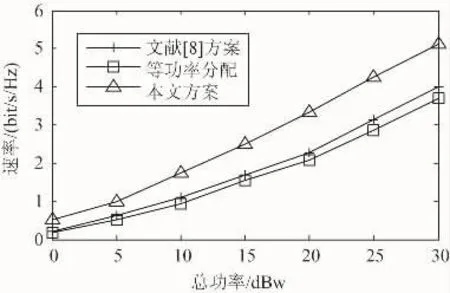
图2 可达总速率随发射总功率的变化曲线

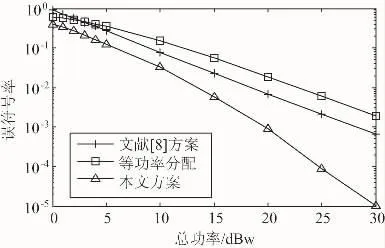
图3 误符号率随发射总功率的变化曲线

3种功率分配算法下系统的误比特率性能如图3所示。从图中可以看出，在低信噪比时，功率分配方案对系统性能的影响相差并不大。当总功率小于5 dBw时，3种方案的区别并不明显。然而随着总功率阈值的提高，在消耗同样功率的情况下，在本研究所提方案下系统的误比特率性能相对其他两种算法依然有很大提高。这是由于在总功率较低的情况下，系统接收信噪比较低，使功率分配方案对系统的影响难以显现。当功率提高时，系统接收信噪比也相对提高，所有节点通过使用本文所提出的功率分配方案，调整每个节点的发射功率大小，进而获得总功率约束条件下的系统优化性能。

图4 可达总速率随中继数目的变化曲线

在中继数目不同的情况下，3种功率分配方法的系统可达总速率的变化曲线如图4所示。此时总功率阈值Pt设为20 dBw。由图可见，系统可达总速率随中继数目的增多而增大，相对于其他两种功率分配策略，本文所提方案在不同中继数目下，系统可达传输速率都有不同程度的提高。当中继数目较少时，系统可达总速率增大较快，当中继数目较多时，由于消耗的总功率不变，系统总速率增加缓慢，并趋于平缓。

下面对算法的复杂度进行分析，由于通信系统对实时性要求较高，所以对功率分配算法的反馈开销和复杂度也有一定的要求。以文献［8］为代表的现有双向多中继功率分配算法，大多要求所有节点已知全部的信道增益信息，这使得中继间的信息交互开销很大。并且现有算法需要用户节点集中式计算功率分配因子，然后分别将功率分配因子传递给各个中继节点造成时间延迟的弊端。而所提算法的实现方式只需要每个中继能够获得各自相邻的信道增益信息，仅两个用户节点需要已知全部信道状态信息，并且能够实现中继功率分配因子在各个中继处分布式计算，用户节点仅需要广播给各个节点功率归一化因子即可，大大减小了反馈开销和计算复杂度，有利于工程实现。

4 结 语

本研究从最大化系统最小传输速率的角度出发，提出了一种双向多中继协同通信系统的功率分配方案。该方案将问题分解为用户节点功率分配和中继节点功率分配两部分，简化了用户节点功率分配，实现了中继节点功率分配因子分布式计算，大大减小了反馈开销和计算复杂度。仿真结果表明，该功率分配方案在系统双向可达速率和误码率两方面均优于现有双向中继功率分配策略，而且性能随着中继数目的增加而提升。未来，考虑两用户节点与各个中继节点统一进行功率最优分配，将是需要进一步研究的方向。

参考文献：

［1］SENDONARISA，Erkip E，AAZHANG B.User Cooperation Diversity［J］.IEEE Transactions on Communication，2003，51（10）：1927-1948.

［2］ZHANG R，LIANG Y C，CHAI C C，et al.Optimal Beamforming for Two-way Multi-antenna Relay Channel with Analogue Network Coding［J］.IEEE Journal Selected Areas in Communications，2009，27（5）：699-712.

［3］OECHTERING T J，JORSWIECK E A，WYREMBELSKIR F et al.On the Optimal Transmit Strategy for the MIMO Bidirectional Broadcast Channel［J］.IEEE Transactions on Communications，2009，57（12）：3817-3826.

［4］芮国胜，王林，张洋，等.分布式双向中继选择算法及用户功率分配［J］.通信学报，2014，35（5）：1-7.

［5］RANKOV B，WITTNEBEN A.Spectral Efficient Protocols for Halfduplex Fading Relay Channels［J］.IEEE Journal on Selected Areas in Communications，2007，25（2）：379-389.

［6］NAM W，CHUNG S，Lee Y H.Capacity Bounds for Two-way Relay Channels［C］.IEEE International Zurich Seminar on Digital Object Identifier.Zurich，Switzerland，2008：144-147.

［7］NOSTRATINIA A，HUUNTER T E，HEDAYAT A.Cooperative Communications in Wireless Networks［J］. IEEE Commun，2004，42（10）：74-80.

［8］WU Z，YANG H B.Power Allocation of Cooperative Amplify-and-forward Communications with Multiple Relays［J］.Journal of China Universities of Posts and Telecommunications，2011，18（4）：65-69.

［9］李勇，张翔，彭木根，等.瑞利双向中继信道的功率分配及中继位置选择［J］.北京邮电大学学报，2012，35（2）：94-28.

［10］吉晓东，郑宝玉，崔景伍.不对称双向中继信道中的再生双向中继选择及功率分配［J］.电子与信息学报，2013，35（7）：1707-1712.

［11］赵睿，傅友华，李春国，等.多天线双向中继系统中的中继处理与资源分配策略［J］.电子与信息学报，2010，32（4）：763-769.

［12］ZHANG J，BAI B，LIY.Outage-optimal Opportunistic Relaying for Two-way Amplify and Forward Relay Channel［J］.Electronic Letters，2010，46（8）：595-597.

［13］HAVARY-NASSAB V A，SHAHBAZPANAHI S，GRAMI A.An SNR Balancing Approach to Two-way Relaying［C］. IEEE Wireless Communication Signal Processing，2009：250-254.

［14］李春国，仲崇显，杨绿溪，等.多中继双向协作转发的分布式实现方案设计及其渐进最优性分析［J］.通信学报，2011，32（6）：45-52.

［15］JING Y，JAFARKHANIH.Network Beamforming Using Relayswith Perfect Channel Information［J］.IEEE Transactions on Information Theory，2009，55（6）：2499-2517.

王 林（1985—），男，博士研究生，主要研究方向为协同通信方向；

E-mail：wl307073874＠126.com

芮国胜（1968—），男，教授。主要研究方向为现代通信系统，小波分析与应用方向；

张 洋（1983—），男，讲师，主要研究方向为混沌与非线性滤波技术等。

Power A llocation Strategy in Two-way M ultip le relays under Lim ited Total Power

WANG Lin1，RUIGuo-sheng2，ZHANG Yang2
（1.Graduate Students'Brigade，Naval Aeronautical and Astronautical University，Shandong Yantai264001，China；2.Department of Electronic and Information Engineering，Naval Aeronautical and Astronautical University，Shandong Yantai264001，China）

In the light of two-way multiple relays Amplify-and-Forward cooperative communication systems，a power allocation strategy based on maximizing the minimum two-way rate criteria is proposed. The power allocation ismade of two kinds of allocations，user's power allocation and relay's power allocation.In the user's power allocation，the allocation is greatly simplified by transforming the multi-relay channels to a single relay channel.In the relay's power allocation，the distributed relays power allocation is achieved by matrix transform.It reduces both the feedback overhead and computational complexity. Simulation results show that the proposed strategy outperforms the existing two-way relay power allocation strategy in terms of both the system sum-rate and bit error rate.The performance is improved as the increasing of the number of relays.

cooperative communication；amplify-and-forward；two-waymultiple relays；power allocation

TN92

：A

：1673-5692（2015）01-107-06

10.3969／j.issn.1673-5692.2015.01.019

2014-12-24

2015-01-19

国家自然科学基金（61179018，41476089）