MDYB-3有机玻璃在不同应变率下的一维屈服行为*

邓 小 秋,李 志 强,周 志 伟,王 志 华,姚 小 虎

(1.太原理工大 学应用力学 与生物医学 工程研究所,山西 太 原 030024; 2.太原理工大学材料强度与结构冲击山西省重点实验室,山西 太原030024; 3.中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室,甘肃 兰州730000; 4.华南理工大学土木与交通学院,广东 广州510641)

MDYB-3有机玻璃在不同应变率下的一维屈服行为*

邓 小 秋1,2,李 志 强1,2,周 志 伟3,王 志 华1,2,姚 小 虎4

(1.太原理工大 学应用力学 与生物医学 工程研究所,山西 太 原 030024; 2.太原理工大学材料强度与结构冲击山西省重点实验室,山西 太原030024; 3.中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室,甘肃 兰州730000; 4.华南理工大学土木与交通学院,广东 广州510641)

对 MDYB-3有机玻璃进行了多组不同应变率(10-3~3 000 s-1)下的压缩实验,得到准静态下的屈服应力与动态下的峰值应力。沿其增强与面内2个方向进行准静态压缩实验,以分析定向拉伸对屈服应力的影响,修正了 Ree-Eyring模型与 Cooperative模型以描述定向有机玻璃的屈服行为。采 用Johnson-Cook模 型描述屈服后的黏塑性行为。结果表明 Cooperative屈服模型比 Ree-Eyring屈服模型更接近实验结果,且 能 准确描述准静态屈服应力。动态压缩下的峰值应力为失效应力,说明试样在1 500 s-1以上应变率下未达到屈服应力时已经发生破坏。Johnson-Cook模型对于单条曲线拟合良好,但无法准确描述材料的应变率相关性。

固体力学;准静态/动态压缩;Johnson-Cook模型;屈服应力;MDYB-3有机玻璃

有机玻璃(polymethyl methacrylate,PMMA)是典型的黏弹性材料,为无定形非晶态的高分子聚合物,内部为由分子链缠绕交联所构成的空间结构,具有明显的应力松弛、蠕变、应变率效应等性质。MDYB-3有机玻璃被广泛应用在航空领域,如飞机舱盖等,近年来鸟撞飞机事故频发,研究其力学性能具有重要意义。

目前对于无定形高聚物的屈服点研究多结合其黏塑性行为分析,将此类聚合物考虑为弹-黏塑性,对于屈服应力 多作定 性分析 。实验 研究方 面主要 研 究 其 应 变 率 相 关 性 ,温 度 相 关 性 等[1-2],很 少 有 理 论对高聚物屈服应力进行定量分析。 关 于 屈 服 应 力 的 研 究 可 追 溯 到 H.Eyring 等[3-4]的 黏 性 理 论 。 在 此基 础 上 ,R.N.Haward 等[5]最 先 以 三 元 件 模 型 描 述 了 材 料 的 黏 塑 性 ,A.S.Argon 等[6]基 于 塑 性 变 形 扭曲 机 制 并 考 虑 温 度 和 应 变 率 ,提 出 了 相 应 的 黏 塑 性 本 构 模 型 。M.C.Boyce等[7]与 E.M.Arruda等[8]以三链结构或八链结构作为研究对象,从热学方面进行研究,考虑了分子链段扭曲导致软化,分子排列的熵变导致硬化等行为。类似的,P.D.Wu等[9]以n条链 结构,使离散结构趋于连 续,并能用三链模 型 与八链模型表示 。L.Anand等[10]以连续介质理论,从 热学 相 关 理 论 得 到 聚 合 物 的 黏 塑 性 描 述,然 而 此 类模型均未单独考虑屈服应力。而国内对于聚合的本构行为研究,多集中于屈服前的行为,如ZWT黏弹性 模 型[11]与 多 Maxwell本 构 模 型[12],而 对 于 屈 服 行 为 及 屈 服 后 的 黏 塑 性 行 为 鲜 有 报 道 。

在对高聚物屈服应力的定量分析中,C.C.Bauwens等[13]以 玻 璃 态 转 变 及 次 级 转 变 两 个 过 程,描 述了 Ree-Eyring屈服模型。D.G.Fotheringham 等[14]考 虑了多 分子链 段的 联 合 流 动,讨 论 了 屈 服 过 程 中的作用力与恢 复力。F.Povolo等[15]结合上 述两者 ,以 联 合 流 动 模 型 代 替 2 个 Eyring 过 程 描 述 了 屈 服应力。在此基础上,J.Richeton等[16-17]运用 WLF 理 论 ,描 述 了 大 范 围 温 度 与 应 变 率 的 屈 服 应 力 ,记 为Cooperative屈服模型。

有机玻璃制备过程中,为了达到一定的应用性能,需对其进行改性,常见方法有共聚增韧、共混增韧、定 向 拉 伸 与 复 合 多 层 等[18]。 MDYB-3 有 机 玻 璃 是 由 聚 甲 基 丙 烯 酸 甲 酯 与 耐 光 剂 组 成,在 超 过 玻 璃化转变温度15~20℃(约135℃)时,对有机玻璃板进行双轴定向拉伸,并冷却固化。沿垂直于板方向(增强方向,Normal direction)的分子链排列较为有序,从而增强了其力学性能,而平行板方向(面内方向,Parallel direction)仍为无序。

而 对 高 聚 物 的 黏 塑 性 研 究,大 多 模 型 参 数 较 多 或 分 析 方 法 过 于 复 杂 ,不 具 有 广 泛 应 用 性[5-10]。Johnson-Cook 模型多 用于金 属材料 的 黏 塑 性 行 为 的 描 述[19-21],尚 没 有 关 于 使 用 Johnson-Cook 模 型 描述定向有机玻璃黏塑性行为的报道。

本文中对 MDYB-3有机玻璃进行了准静态与动态(10-3~3 000 s-1)压缩实验,同时沿增强方向和面内方向进行应变率10-3s-1的压缩实验,根据增强方向与面内方向屈服应力的关系,修正 Ree-Eyring模型与 Cooperative模型在准静态压缩下对屈服应力的描述,并以此判断动态压缩是否达到屈服应力。结果表明:Cooperative屈服模型比 Ree-Eyring屈服模型更接近实验结果,且能准确描述准静态屈服应力。Johnson-Cook模型对于单条曲线拟合良好,但无法准确描述材料的应变率相关性。

1 实 验

MDYB-3有机玻璃由中国建材研究总院提供,准静态和动态压缩实验分别在国产万能材料试验机与SHPB装置上完成,实验环境温度分别约为5℃和13℃。试件均由5 mm 厚的有机玻璃板加工而成。准静态实验试件尺寸⌀5 mm×5 mm,动态实验试件尺寸⌀10 mm×5 mm,沿增强方向加载。加工边长5 mm的立方体试件,分别沿增强方向和面内方向加载。SHPB入射杆与透射杆均为高强钢,长度400 mm,子弹长度200 mm,直径均为14 mm。准静态实验应变率范围为0.001~1 s-1,动态实验应变率范围为1 500~3 000 s-1,立方体试件在2个方向的应变率均为0.001 s-1。

实验前后典型的材料变形与破坏如图1所示,所得应力应变曲线如图2所示,实验具有很高的重复性,从图2可得到各个应变率下的屈服应力和峰值应力。结合变形破坏模态与应力应变曲线,材料具有明显的应变率效应,屈服应力随应变率增大而增大。准静态压缩下,材料屈服主要表现为韧性,其破坏应变至少可达0.35以上,较低应变率下甚至可达0.5。而动态压缩主要表现 为 脆 性,应变达0.1~0.2时,已经破坏失效,然而对于材料的峰值应力是否达到屈服应力并无定论。本文中将从屈服模型得到屈服应力,与实验得到峰值应力对比说明这一问题。

图1 实验前后 MDYB-3有机玻璃的压缩变形形态Fig.1 Deformation of MDYB-3 PMMA before and after compression tests

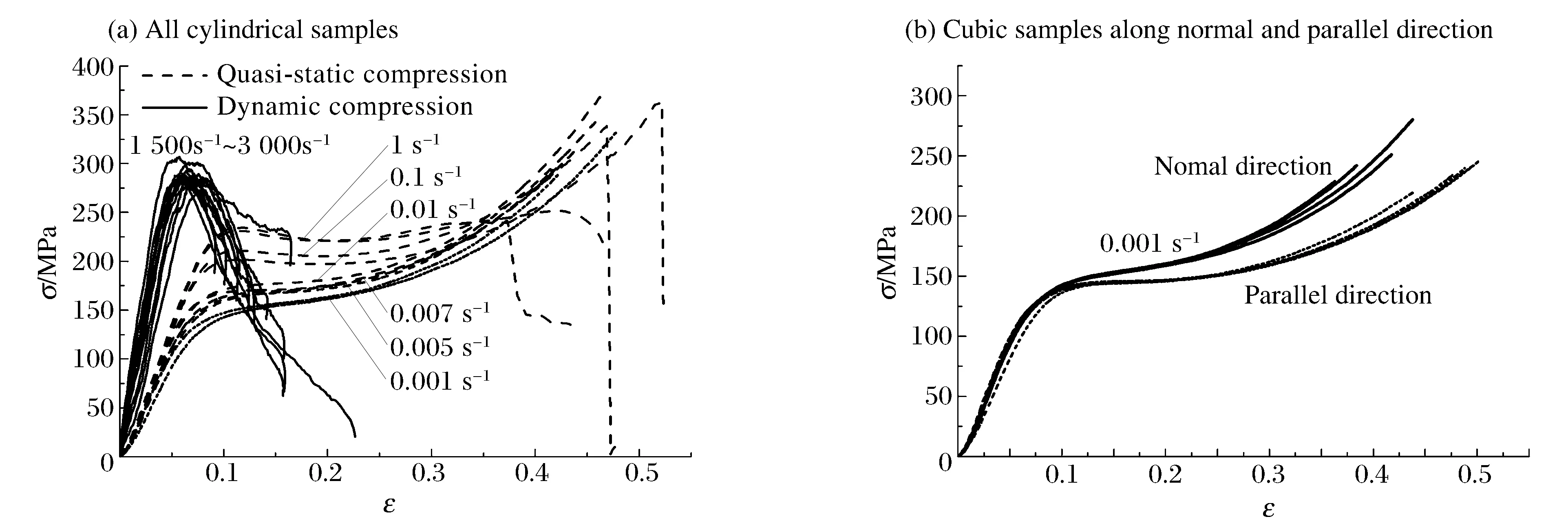
图2 实验所得有机玻璃应力应变曲线Fig.2 The stress of PMMA varied with strain in tests

实验中材料呈现出的屈服行为可从2个方面进行分析[7],一方面存在分子链段的运动,使其出现应变软化现象;另一方面,分子链段运动,逐渐排序有序,导致熵变阻力增大,使材料出现应变硬化的现象。两方面此消彼长,共同导致了材料的黏塑性行为。在较低应变率条件下,屈服应力不明显,因为实验温度较低,分子链段运动能力较弱,抑制了应变软化;同时定向拉伸后使分子沿垂直板方向变得有序,增强了应变硬化。对于此类曲线,若按照0.2%残余应变取其屈服应力,因加载前期出现非线性且该取法多用于金属材料,误差较大,取应变为0.12时的应力为屈服应力。

从图2(b)中不难发现,应变率同为 0.001 s-1条 件下,屈服前,增强方向与 面 内 方向的结果完 全 一致,说明有机玻璃的分子链排序不影响其刚度,且其黏弹性行为完全一致。屈服后,增强方向的流动应力明显高于面内方向。与上述讨论相似,等温同应变率下,其分子链段的变形移动能力相近,然而经过热拉冷固加工后,增强方向比面内方向具有更高的有序性,从而增加了其变形的熵变阻力,增强了应变硬化效应,使其屈服应力不明显。从图中可得到增强方向的屈服应力为151.7 MPa,面内方向的屈服应力为143.9 MPa。

2 理论模型

2.1 Ree-Eyring屈服模型

最初的 Ree-Eyring模型是 基于其 黏 性 定 理[3-4],描 述 屈 服 的 产 生 是 因 为 高 聚 物 内 部 分 子 链 发 生 了移动,产生剪切应力,使高分子结构内部发生黏性流动。然而有机玻璃随温度或应变率变化会出现玻璃态 转 变(α转 变)和 低 温(或 高 应 变 率)下 的 次 级 转 变 (β转 变 ),C.C.Bauwens等[13]则 同 时 考 虑 了 次 级 转变,将 Ree-Eyring屈服模型分开成α转变与β转变2项进行描述:

式 中 :σy为 一 维 屈 服 应 力 ,T 为 绝 对 温 度 ε为 应 变 率 ,k=1.38×10-23J/K,为 波 尔 兹 曼 常 数 ;Aα= 6.958 kPa/K,Aβ=36.652 kPa/K,Cα=5.00×10-52s和 Cβ=4.67×10-17s为 活 化 相 关 参 数;Qα= 412 kJ/mol,Qβ=107 kJ/mol分别为α转变与β转变对应活化能。

美国历史游径标识内容以图文并茂的形式，包含有环境保护、自然和地理知识等多种内容，结合现场实景，打造出一处处科普课堂。一方面，为提高科普宣传效果，各地定期组织志愿者带领青少年学生重走游径，志愿者由专家学者、环保志愿者等组成，以标识展示的科普内容为重点，结合场景的变化为学生讲授各类科普知识，普及家乡历史。另一方面，通过标识反映紧迫的环境危机，以流程图、分析图等图示表达环境变化或污染治理过程，为便于儿童理解，部分标识的演示图片以卡通画呈现，增强了标识的科学性和可读性（图4）。

2.2 Cooperative屈服模型

在 Ree-Eyring黏性 理论基 础 上,J.Richeton 等[16]用 联 合 流 动 模 型 代 替 了 Ree-Eyring 模 型 中 的α与β转变对屈服应力的影响,并推断活化能为β松弛时的能量,提出了 Cooperative屈服模型。该模型描述了材料的应变率和温度相关性,并通过时/温等效理论(WLF),将可描述温度范围扩展到玻璃态转变温度以上。描述玻璃态温度以下屈服应力的具体表达式为:式中 :σ(0)为 0 K 时 的 内 部 应 力 ,为 屈 服 应 力 与 有 效 应 力 之 差 。m 为 材 料 参 数 ,V 为 活 化 体 积 ,T 为 绝 对温 度 ,k为 波 尔 兹 曼 常 数 ,n为 描 述 分 子 链 段 联 合 移 动 的 材 料 参 数 ε0为 前 置 指 数 应 变 率 ,ΔHβ为β松 弛活化能,具体参数可参考文献[16]。

2.3 Johnson-Cook模型

Johnson-Cook 是一个 基于实 验,通过数值 方法得 到 的 唯 象 模 型[22],可 用 于 描 述 应 变 率 和 温 度 相 关的黏塑性行为,在金属领域被广泛应用,其具体表达式为:

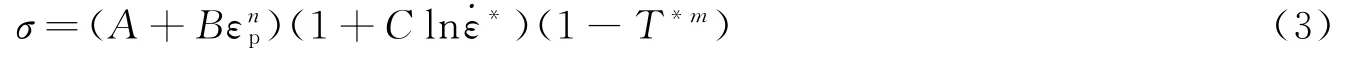
式 中 :σ和ε 分 别 为 等 效 流 动 应 力 和 等 效 塑 性 应 变 ,一 维 条 件 下 为 实 验 得 到 的 应 力 与 塑 性 应 变 ε*为 量纲 一 塑 性 应 变 率,ε*=ε/ε0ε为 应 变 率 ε0为 参 考 应 变 率 ,取 0.1 s-1;T*=(T -Tr)/(Tm-Tr),T为 绝 对 温 度,Tr和 Tm分 别 为 室 温 和 熔 点 ;A、B、n、C、m均 为 材 料 参 数 。

3 结果和讨论

3.1 屈服行为

在应用上述模型时,所使用的材料参数均来自普通有机玻璃,未进行定向拉伸处理,而本文中研究对象为 MDYB-3有机玻璃,根据0.001 s-1下立方体试件的实验研究,可得增强方向屈服应力比面内方向屈服应力高,因此需要对模型进行修正。

Cooperative屈服模型修正为:

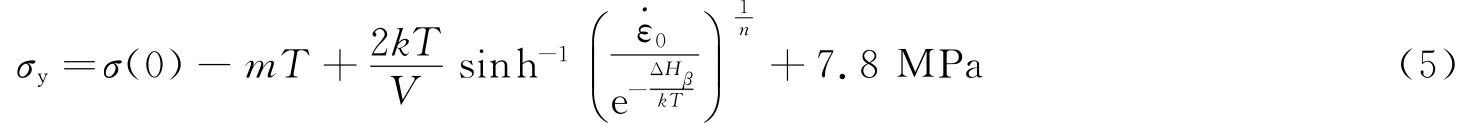
准静态压缩实验得到屈服应力、修正后的 Ree-Eyring屈服模型与 Cooperative屈服模型在5 ℃下的屈服应力-对数应变率曲线,如图3 所示。结果显示 Cooperative屈服模型要优于 Ree-Eyring模型, Cooperative屈服模型能准确描述实验的屈服应力,而 Ree-Eyring模型要比实验值低。这与文献结果相似,造成2个模型差别的原因是两者对于屈服应力描述的依据及分析不同。

上述实验结果显示,在高速冲击下(1 500~3 000 s-1),MDYB-3有机玻璃已经破坏,然而无法判定其是否达到屈服应力后才破坏。图4所示为13℃时,动态压缩实验得到峰值应力(图中实验点)和修正前后屈服应力与对数应变率的关系。动态压缩实验的峰值应力很接近此 Ree-Eyring屈服应力,但仍普遍小于该值,且均小于此 Cooperative屈服应力。而未修正的2个模型可用于描述非定向有机玻璃,因此可得到 MDYB-3有机玻璃动态失效应力小于非定向有机玻璃的屈服应力。

从图中还可以看出,峰值应力非常接近理论曲线,说明材料已经进入塑性段。分别以修正后的Ree-Eyring屈服模型与 Cooperative屈服模型的屈服应力-对数应变率曲线比较。显然只有2个峰值应力点才大于修正 Ree-Eyring屈服应力,而小于修正 Cooperative屈服应力;大部分峰值点均未达到修正Ree-Eyring屈服应力。可以认为 MYDB-3在本文中实验温度,动态冲击范围内(1 500~3 000 s-1)下,未达到屈服应力状态已经失效破坏。

MDYB-3有机玻璃的屈服与失效行为可从微观进行解释,在材料进入塑性段后,分子链段开始局部移动。低应变率时,材料表现韧性,未出现明显裂纹,分子链段的移动增多及增强,达到屈服应力后出现应变软化。在动态条件下,应变率较高,进入塑性段后,分子移动的同时出现了银纹,应变逐渐增大时,分子移动还没有达到软化点,银纹已逐渐扩展成裂纹,导致材料失效破坏。MDYB-3有机玻璃在应变率1 500~3 000 s-1动态冲击下未达屈服应力即破坏,可以得到在更高应变率条件下,试件的松弛时间更短,也将出现未达到屈服应力即破坏的现象,在1 500 s-1以上应变率均有这种特性。

图3 修正屈服模型的准静态屈服应力与应变率对数曲线Fig.3 The quasi-static stress of the two revised yield models varied with the logarithmic strain rate

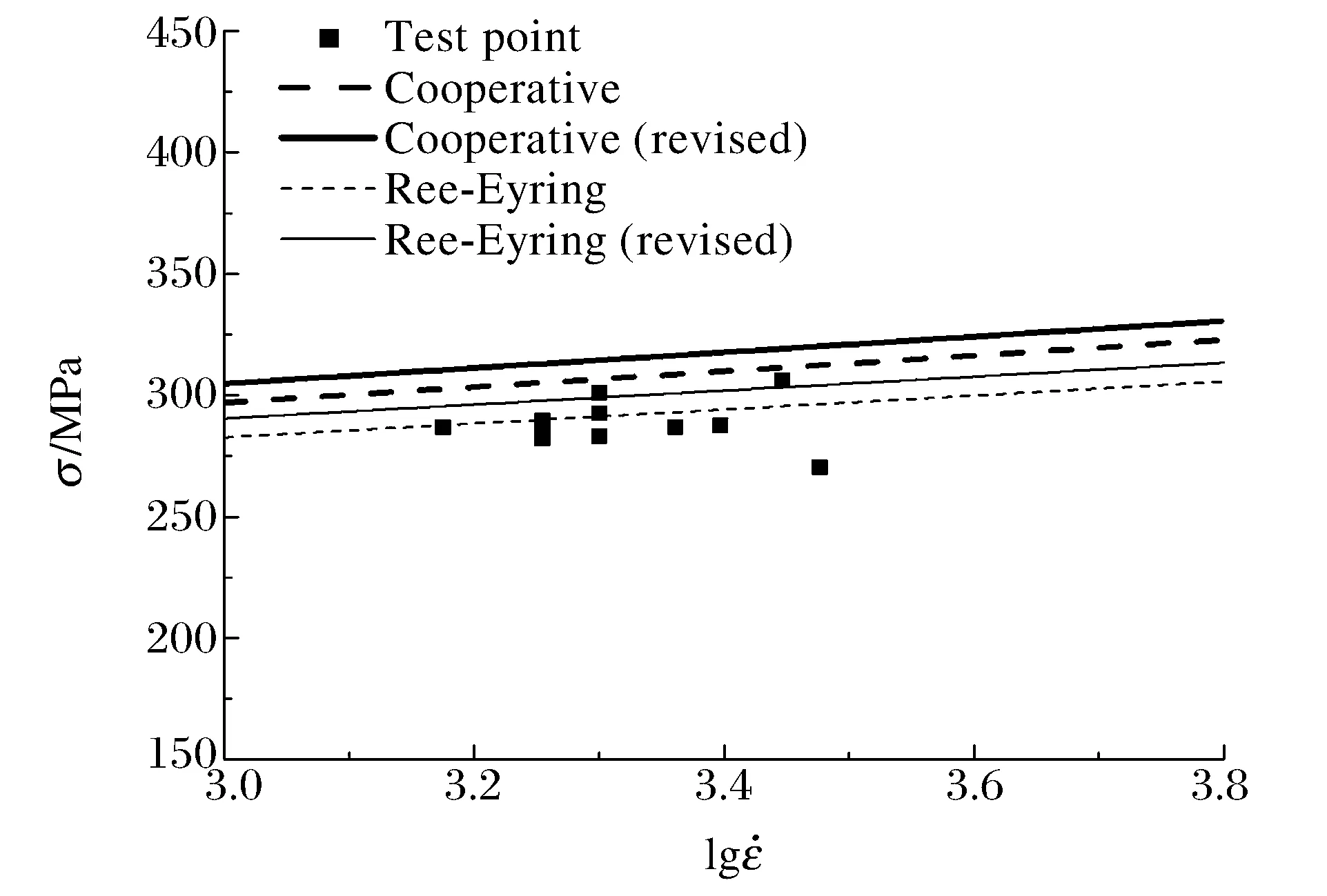
图4 修正屈服模型的动态应力与应变率对数曲线Fig.4 The dynamic stress of the two revised yield models varied with the logarithmic strain rate

3.2 黏塑性行为

对 MDYB-3有机玻璃的黏塑性行为进行描述时,需要先确定塑性起点。Johnson-Cook模型最初用于金属材料,而对于金属材料,弹性范围一般不存在黏性影响,且屈服应力离塑性起点很近,可近似将屈服应力作为塑性起点。而 MDYB-3有机玻璃具有典型的黏弹性,其屈服前的非线性区域较大。本文中将不考虑屈服前黏性的影响,得到弹-黏塑性本构,尝试使用2种方法得到塑性起点:(1)认为弹性极限为塑性起点;(2)参考金属材料做法,将屈服极限作为塑性起点,只描述屈服极限后的黏塑性行为。

2种方法均选取0.1 s-1作为参考应变率,同在室温下,温度相关的最后一项乘子变成1,对结果没影响,Johnson-Cook模型简化为:

图5所示为以弹性极限作为塑性起点时,式(6)的曲线。先对黏弹性段近似直线的区域拟合直线(图中虚线所示),确定弹性极限时的应变为0.059,并以其作为塑性零点。对于参考应变率下的曲线,ε*=1,最 后 一 项 乘 子 也 变 成 1。 总 应 变 为0.059对 应 塑 性 应 变εnp=0,则 塑 性 起 点 应 力 即 为 模 型 中 的 A =153 MPa。以最小二乘法拟合时,不考虑后部强化段,得到B=64.9 MPa,n=0.161。显然拟合结果与实验结果相差很远,即无法使用Johnson-Cook模型原始定义对曲线进行拟合。

以屈服极限作为塑性起点时,采用上述相同的方法,先根据参考应变率下的单条曲线,对式(6)进行拟合,此时应变率相关项变成1,根据屈服极限点(0.109,201 MPa),得到A=201 MPa。然后使用最小二乘法拟合参考应变率曲线,得 到B=3 280 MPa、n=3.38。 最后确 定式(6)中的参数C,对于 各 应 变 率下 塑 性 应 变εnp为 0 的 点 ,根 据 准 静 态 屈 服 应 力 与 应 变 率 的 关 系 ,可 拟 合 得 到C为0.062 6。

于是得到 MDYB-3有机玻璃的Johnson-Cook本构关系为:

因为准静态压缩在5 ℃下进行,动态压缩在13 ℃下进行,为了描述动态压缩,还需要引入式(3)中的温度相关项。在应变率相同情况下,温度差别导致的应力差别与(Tm-T)成正比,MDYB-3有机玻璃 为 非 晶 结 构,无 固 定 熔 点,Tm取 其 软 化 温 度 118 ℃[23],则 可 通 过 该 比 例将5℃ 时 的 动 态Johnson-Cook模 型 转 换 到13℃ 。 图6给 出 了 应 变 率 为1 800和2 800 s-1时,式(7)中Johnson-Cook本构 关 系 曲 线 与 实 验 曲 线 的 对 比 。 从 图 中 可 以 看 出,参 考 应 变 率0.1 s-1的 实 验 曲 线 拟 合 较 为 吻 合,其 他准静态应变率的实验曲线均从屈服极限开始发生偏离。

观察Johnson-Cook模型规律,在描述不同应变率时接近平行,而实际实验过程中,材料的应变硬化与应变率紧密相连,随应变率增大,应变硬化速度有所减缓,这与松弛时间减小有关,而Johnson-Cook模型未能描述此状态。同时,无论使用哪种方法,Johnson-Cook模型都是单调递增的,也无法描述材料的应变软化行为。对于动态压缩,Johnson-Cook模型起点(屈服应力)要高于峰值应力,可结合上述对屈服应力的比较,因材料破坏,应力随应变急速下降,而本文中的修正Johnson-Cook模型描述了理想的黏塑性行为,没有考虑损伤,自然无法对应。

图5 塑性起点为弹性极限的修正Johnson-Cook公式曲线Fig.5 Revised Johnson-Cook model with the plastic starting point of elastic limit

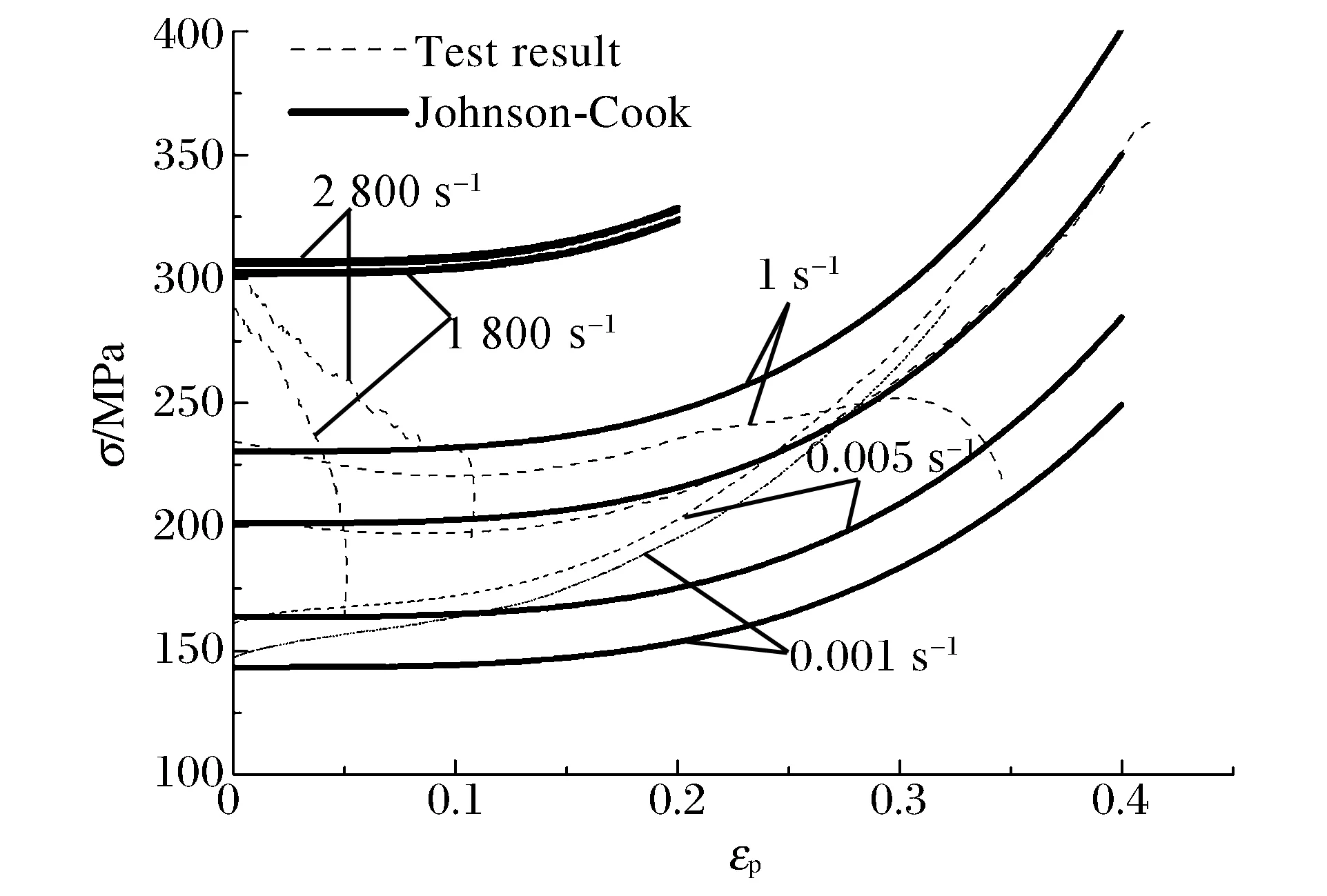
图6 塑性起点为屈服极限的修正Johnson-Cook公式曲线Fig.6 Revised Johnson-Cook model with the plastic starting point of yield limit

4 结 论

本文中对 MDYB-3有机玻璃进行了多组不同应变率下(10-3~3 000 s-1)的压缩实验,得到各屈服应力与动态下的峰值应力,同时对立方体试件进行了不同方向的屈服行为研究。修正了 Ree-Eyring屈服模型与 Cooperative屈服模型以描述 MDYB-3有机玻璃。结果表明修正 Cooperative屈服模型能准确描述准静态屈服应力,比 Ree-Eyring屈服模型较好。判定了动态压缩下的峰值应力为失效应力,且材料在1 500 s-1以上应变率条件下,未达到屈服应力已发生破坏。

使用Johnson-Cook模型描述 MDYB-3黏塑性行为时,需以屈服应力对应点为塑性开始点,模型对参考应变率下结果拟合良好,而无法描述其他应变率下的行为,且无法描述应变软化现象。若要使用该模型,需先修正其对应变率及温度相关性的描述。

[1]Li Zhou-hua,Lambros J.Strain rate effects on the thermomechanical behavior of polymers[J].International Journal of Solids and Structures,2001,38(20):3549-3562.

[2]Chen W,Lu F,Cheng M.Tension and compression tests of two polymers under quasi-static and dynamic loading [J].Polymer Testing,2002,21(2):113-121.

[3]Eyring H.Viscosity,plasticity,and diffusion as examples of absolute reaction rates[J].The Journal of Chemical Physics,1936,4(4):283-291.

[4]Taikyue R,Eyring H.Theory of non-Newtonian flow:Ⅰ:Solid plastic system[J].Journal of Applied Physics, 1955,26(7):793-800.

[5]Haward R N,Thackray G.The use of a mathematical model to describe isothermal stress-strain curves in glassy thermoplastics[J].Proceedings of the Royal Society of London A,1968,302(1471):453-472.

[6]Argon A S.A theory for the low-temperature plastic deformation of glassy polymers[J].Philosophical Magazine, 1973,28(4):839-865.

[7]Boyce M C,Parks D M,Argon A S.Large inelastic deformation of glassy polymers:PartⅠ:Rate dependent constitutive model[J].Mechanics of Materials,1988,7(1):15-33.

[8]Arruda E M,Boyce M C.A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials[J].Journal of the Mechanics and Physics of Solids,1993,41(2):389-412.

[9]Wu P D,Giessen E V D.On improved network models for rubber elasticity and their applications to orientation hardening in glassy polymers[J].Journal of the Mechanics and Physics of Solids,1993,41(3):427-456.

[10]Anand L,Gurtin M E.A theory of amorphous solids undergoing large deformations,with application to polymeric glasses[J].International Journal of Solids and Structures,2003,40(6):1465-1487.

[11]王 礼立,Pluvinage G,Labibes K.冲击 载 荷 下 高 聚 物 动 态 本 构 关 系 对 粘 弹 性 波 传 播 特 性 的 影 响 [J].宁 波 大 学 学报 :理工 版,1995,8(3):30-57. Wang Li-li,Puvinage G,Labibes K.The influence of dynamic constitutive relations of polymers at impact loading on the viscoelastic wave propagation character[J].Journal of Ningbo University:Natural Science and Engineering Edition,1995,8(3):30-57.

[12]吴 衡毅,马钢 ,夏源 明.PMMA 低、中应变率单 向拉伸力学 性能的实验 研究[J].实 验力学,2005,20(2):193-199. Wu Heng-yi,Ma Gang,Xia Yuan-ming.Experimental study on mechanical properties of PMMA under unidirectional tensile at low and intermediate strain rates[J].Journal of Experimental Mechanics,2005,20(2):193-199.

[13]Bauwens C C,Bauwens J C,Homès G.Tensile yield-stress behavior of glassy polymers[J].Journal of Polymer Science Part A-2:Polymer Physics,1969,7(4):735-742.

[14]Fotheringham D G,Cherry B W.The role of recovery forces in the deformation of linear polyethylene[J].Journal of Materials Science,1978,13(5):951-964.

[15]Povolo F,Hermida E B.Phenomenological description of strain rate and temperature-dependent yield stress of PMMA[J].Journal of Applied Polymer Science,1995,58(1):55-68.

[16]Richeton J,Ahzi S,Daridon L,et al.A formulation of the cooperative model for the yield stress of amorphous polymers for a wide range of strain rates and temperatures[J].Polymer,2005,46(16):6035-6043.

[17]Richeton J,Ahzi S,Vecchio K S,et al.Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers:Characterization and modeling of the compressive yield stress[J].International Journal of Solids and Structures,2006,43(7/8):2318-2335.

[18]董 绍胜,魏月 贞,白 永平,等.耐热有机玻 璃的研制[J].高 分子材 料科 学与工 程,2000,16(1):173-175. Dong Shao-sheng,Wei Yue-zhen,Bai Yong-ping,et al.Study on the heat resistant PMMA[J].Polymer Materials Science and Engineering,2000,16(1):173-175.

[19]胡 昌明,贺红 亮,胡 时胜.45号钢的 动态力学性 能研究[J].爆炸与冲击 ,2003,23(2):188-192. Hu Chang-ming,He Hong-liang,Hu Shi-sheng.A study on dynamic mechancial behaviors of 45 steel[J].Explosion and Shock Waves,2003,23(2):188-192.

[20]张 宏建,温卫 东,崔 海涛,等.不同温度下IC10合 金的本 构关系[J].航空 学报,2008,29(2):499-504. Zhang Hong-jian,Wen Wei-dong,Cui Hai-tao,et al.Constitutive analysis of alloy IC10 at different temperatures [J].Acta Aeronautica Et Astronautica Sinica,2008,29(2):499-504.

[21]林 木森,庞宝 君,张 伟,等.5A06 铝合金的动 态本构关系 实验[J].爆 炸与冲击,2009,29(3):306-311. Lin Mu-sen,Pang Bao-jun,Zang Wei,et al.Experimental investigation on a dynamic constitutive relationship of 5A06 Al alloy[J].Explosion and Shock Waves,2009,29(3):306-311.

[22]Johnson G R,Cook W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperatures[C]∥Proceedings of the 7th International Symposium on Ballistics.Netherlands:International Ballistics Committee,1983:541-547.

[23]《中国航 空材 料手册》编辑委员 会.中国航 空材料手册[M].2版.北京 :中国标准 出版社,2001.

One-dimensional yield behavior of MDYB-3 polymethyl methacrylate at different strain rates

Deng Xiao-qiu1,2,Li Zhi-qiang1,2,Zhou Zhi-wei3, Wang Zhi-hua1,2,Yao Xiao-hu4
(1.Institute of Applied Mechanics and Biomedical Engineering, Taiyuan University of Technology,Taiyuan 030024,Shanxi,China; 2.Shanxi Key Laboratory of Material Strength and Structure Impact, Taiyuan University of Technology,Taiyuan 030024,Shanxi,China; 3.State Key Laboratory of Frozen Soil Engineering, Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences,Lanzhou 730000,Gansu,China; 4.School of Civil Engineering and Transportation,South China University of Technology, Guangzhou 510641,Guangdong,China)

Several groups of compression tests at different strain rates(10-3~3 000 s-1)are carried out for MDYB-3 polymethyl methacrylate.Yield stress in the quasi-static tests and peak stress in the dynamic tests are obtained.Compression tests are performed along normal direction and parallel directions of samples to analyze the effect of orientation stretching on yield stress.Ree-Eyring model and Cooperative model are revised to describe the yield behavior of directional PMMA.Viscoplastic behaviors after yield are attempted to be described using Johnson-Cook model.The results of Cooperative yield model are shown to be closer to the test results than those of Ree-Eyring yield model.Cooperative yield model can describe the yield stress of quasi-static tests accurately.Peak stress in dynamic compression test is failure stress,which means that samples fail before yield at the strain rate above 1 500 s-1.The fitting results reveal that Johnson-Cook model can describe a single stress-strain curve well,but it cannot predict the dependence of strain rate.

solid mechanics;quasi-static/dynamic compression;Johnson-Cook model;yield stress; MDYB-3 polymethyl methacrylate

O347.3国标学科代码:1301520

:A

10.11883/1001-1455-(2015)03-0312-08

(责任编辑 王易难)

2013-11-11;

2014-03-04

国家自然科学基金项目(11072166);国家国际科技合作专项项目(2011DFA53080);山西省高等学校优秀青年学术带头人基金项目(2011)

邓小 秋(1988— ),男,硕士研 究生;通 讯作者:李志强,lizhiqiang@tyut.edu.cn。