水/气多介质问题的界面处理方法*

徐 爽,赵 宁,王春武,王东红

(1.南京 航空航天大 学航空宇航 学院,江苏 南 京 210016; 2.南京航空航天大学理学院,江苏 南京210016)

水/气多介质问题的界面处理方法*

徐 爽1,赵 宁1,王春武2,王东红2

(1.南京 航空航天大 学航空宇航 学院,江苏 南 京 210016; 2.南京航空航天大学理学院,江苏 南京210016)

针对不可压缩可压缩水/气多介质问题,提出一种新的界面处理方法。在可压缩水/气界面处构造Riemann问题,在水中设音速趋于无穷大,求解 Riemann问题得到不可压缩可压缩水/气界面处流体的准确流动状态;然后以此状态结合 GFM(ghost fluid method)方法分别为2种流体定义界面边界条件,将两相流 问题转化为单相流问题计算,通过求解level set方程来跟踪界面的位置。对各种不同的界面边界条件定义方法进行了比较,数值模拟结果表明算法能准确地捕捉各类间断的位置,证明了算法的有效性和稳健性。

爆炸力学;Riemann问题;GFM 方法;level set;水/气界面 ;多介质流 动

在多介质问题的数值模拟中,由于水/气物质属性的巨大差异,使得水/气多介质问题成为多介质问题的难点之一。针对具有大密度比的水/气多 介质 问 题,传 统 方 法 主 要 有 3 类[1]:(1)水/气 皆 被 作 为 可压缩流体处理,其中水的状态方程为 Tait方程;(2)水/气皆作为不可压缩流体,这类方法往往用来处理低速水/气多介质运动;(3)水作为不可压流体,气作为可压缩流体,相应的分别采用不可压方程和可压缩欧拉方程作为水/气的流场控制方程。对于第1类方法,由于界面两边的物质属性差异较大,过大的密度比和状态方程差异,容易在界面处产生非物理震荡,并且由于水的刚性很强,声速较大会导致计算时间步长过小,降低计算效率。第2类方法在处理气体中有激波存在以及高速问题时会遇到困难,通常用来模拟低速多介质运动,如水中气泡上升,静止水滴下落等。采用第3类方法时,充分考虑到水/气物理属性差异,可以处理气体中有激波等高速运动问题,问题的关键在于如何给定合适的水/气界面边界条件,使得界面边界条件能更合理的反映出水/气界面处真实的流动状态。

R.P.Fedkiw 等[2]提出了用 GFM 方法来处理多介质问题界面边界条件,最初只是用来处理气气多介质问题,有效的 抑制了 在界面 处产生 的非物 理震荡 。T.G.Liu等[3-4]在 其 基 础 上 发 展 了 MGFM 方 法(modified ghost fluid method),通过在界面处定义 Riemann问题,并利用 Riemann问题的解定义了界面处虚拟流体点的速度和压力值,通过等熵修正定义了真实流体点和虚拟流体点的密度值,MGFM 方法可以有效的处理各种气气多介质问题,但是在处理类似激波阻尼的临界问题时会遇到困难;C.W. Wang等[5-6]提出了 RGFM 方法(real ghost fluid method),利用 Riemann问题的解不 仅 定 义 了 虚 拟 流体点的值,而且对真实流体中点的密度,速度和压力都进行了更新,使得在界面处的流体状态满足接触间断的性质,得到了更加准确的界面边界条件。利用上述几种GFM 方法在处理水/气多介质问题时,把水作为可压缩流体处理,状态方程采用 Tait方程。而当将水作为不可压流体,气体作为可压缩流体处理时,在界面处需要采用更加合理的界面边界条件,才能满足由于界面两边不同的控制方程和物质属性差异对界面处真实流动 状 态 的 影响。针 对 水/气多 介 质 问题,R.Caiden 等[1]提 出 了 new GFM 方法,界面处的速度采用界面附近水的速度值,而将界面附近气体的压力直接作为界面处的压力。数值结果表明,该方法在一定程度上可以有效地捕捉物理现象。

new GFM 方法给出的界面边界条件过于简单,并不能充分反应出界面处真实的流动状态,特别是当界面两边水/气的物质属性差异很大时。由于流体的流动性质很大程度上是物质属性相关的,因此界面处的流动状态通常非线性的依赖于界面两边流体的物质属性。在文献[7-9]中有以下结论:在有限区域内,在马赫数趋于零的情况下,无黏不可压缩方程是欧拉方程的收敛极限。在这个结论的基础上,考虑在界面处定义新的水/气 Riemann问题,其中可以把水视为声速趋于无穷大的可压缩流体,并求解Riemann问题的解,从而得到界面处的真实流体状态。在本文中,利用得到的 Riemann问题的解分别采用 MGFM 与RGFM 这2种方法定义水/气界面边界条件。通过一维数值模拟实验,以及与利用new GFM 方法的计算结果比较分析,2种定义界面边界条件的方法均能有效的捕捉到激波与界面的位置,同时分析3种方法的计算结果的差异及其原因。

1 控制方程

1.1 可压缩流体控制方程

一维无黏可压缩流体控制方程为欧拉方程:

式 中 :ρ为 密 度 ,u为 速 度 ,p为 压 力 ,为 体 积 总 能 ,e为 质 量 内 能 。 理 想 气 体 状 态 方 程 为,其 中

1.2 不可压缩流体控制方程

采 用 投 影 法 求 解 不 可 压 控 制 方 程,对 式(2)关 于x方 向 求 偏 导 得 到,由 于 密 度 为 常 数,则有。 表 明p为 常 数,那 么 在 不 可 压 流 体 区 域 内 的 压 力 满 足 线 性 关 系 式,即 有,其 中xpr和pl分 别 为 不 可 压 流 体 区 域 左 右 两 个 端 点 上 的 的 压 力 值,l为 不 可 压 区 域 的 长 度 。

1.3 Level set方 程

通过求解level set方程隐式追踪界面:

Level set函 数初始 化为距 离符号 函数,空间方向离散采用五阶 WENO 格式[10],时间方向离散则采用三阶 TVD Runge-Kutta方法。

2 界面边界条件

在 new GFM 方法[1]中,只是简单地直接取界面附近真实气体的压力作为界面处的压力 值,界面的速度取临近界面处水的速度值。事实上界面处的流动状态都是与物质相关的,界面处的流动状态非线性的依赖于界面两边介质的物质属性,由于水/气的物质属性差异很大,应考虑到其对界面处真实流动状态的影响。在 MGFM 和 RGFM 方法中,水作为可压缩流体处理,采用刚性较强的 Tait方程作为其状态方程,通过在界面处定义气气 Riemann问题,求解给出了界面处的流体状态,体现了界面两边水/气的物质属性对于界面处流动状态的影响。但是考虑到水作为不可压流体时,具有密度不变等性质,不能求解气气 Riemann问题,上述方法则无法成立。当将水作为不可压流体处理时,在文献[9]中,有以下结论:随着流体马赫数趋向于零,可压缩欧拉方程组的解会收敛到无黏不可压流体方程组的解。另外,R.Agemi[7]证明了在有限区域内,当马赫数趋向于零时,无 黏可压缩流体会 收 敛 为相应的无黏 不 可压流体。基于以上结论,考虑将不可压流体作为声速无穷大的可压缩流体处理,在这一基础上,定义新的针对水/气的 Riemann问题,并求解出 Riemann问题的解,利用其定义更合理的水/气界面边界条件。

2.1 水/气 Riemann问题

在 水/气 界 面 处 ,定 义 Riemann问 题 ,初 始 条 件ρl,ul,pl和ρr,ur,pr分 别 为 界 面 左 右 两 侧 的 密 度 ,速度和压力。为不失一般性,假设左侧为气体,右侧为水。根据以上结论:无黏不可压流体是可压缩流体在声速趋向于无穷大时的收敛极限。在求解水/气 Riemann问题时可以将水作为声速趋向于无穷大的可压流体处理。可压缩流体中的 Riemann问题可以用双激波近似方法求解,双激波近似求解 Riemann问题有以下关系式:

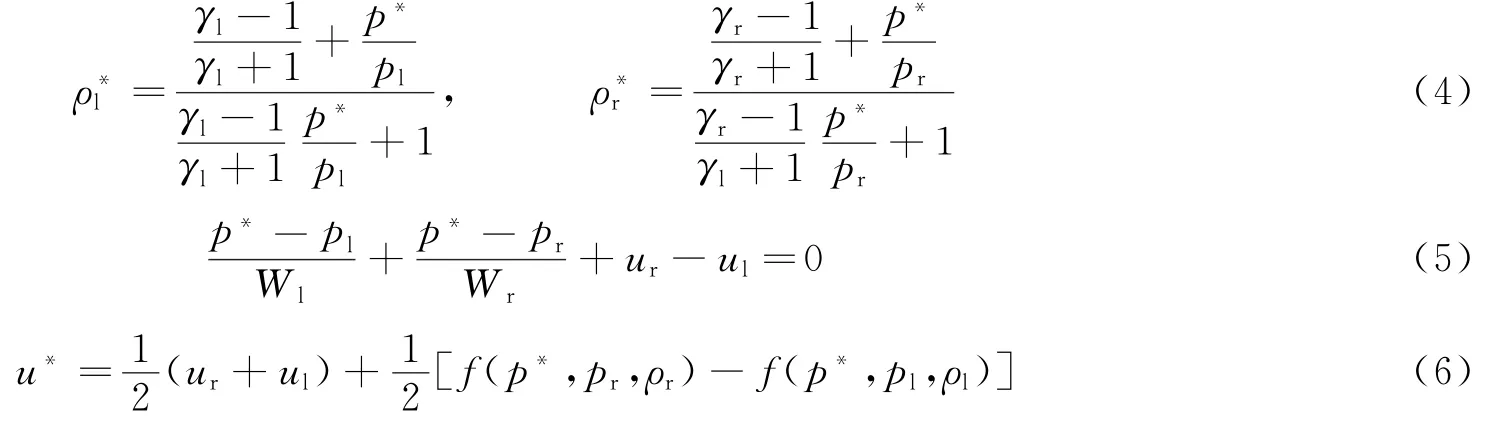
2.2 定义界面边界条件

在处理多介质问题时,GFM 通过定义虚拟流体点来给定合适的界面边界条件。首先,在水/气界面处建立求解水/气 Riemann问题,利用得到的 Riemann问题的解,定义界面处真实流体点和虚拟流体点的流体状态值,从而给定合适的界面边界条件。在得到的水/气 Riemann问题解的基础上,本文中采用两种方式定义界面边界条件,分别为 MGFM 方法和RGFM 方法。

如图1所示,界面在网格点i与i+1之间,气体在界面左侧,水在界面的右侧,取网格点和2的流场状态分别作为 Riemann 问 题的 初 始 左 右 状 态值,求 得 相 应 的 解。接 触 间 断 左 侧 状 态 为,右 侧 状 态 为。 在 MGFM 方 法 中[3],定 义 气 体 界 面 边 界 条 件 ,利 用 得 到 的 Rie-mann问题的解左侧状态 定义网格点i+1上的虚拟流体点的速度和压力,网格点i+2和i+3处的速度和压力取当地真实流体点的值,在求得界面左侧熵值的基础上利用等熵修正得到网格点i上真实流体 以 及 网 格 点i+1、i+2、i+3 上 出 虚 拟 流 体 的 密 度 值 ,上 述 则 给 定 了 气 体 的 界 面 边 界 条 件 。 可 以 采 用类似方法定义水的界面边界条件,值得注意的是,Riemann问题的解中界面右侧状态中的密度也是保持不变的,满足水的密度不变的性质,虚拟点上的密度都为水的密度。

图1 利用 MGFM方法对气体定义界面边界条件Fig.1 The definition of interface boundary condition for gas by MGFM method

如 图 2 所 示 ,在 RGFM 方 法 中[6],对 于 气 体 ,得 到 的 Riemann 问 题 解 的 左 侧 状 态直接定义了网格点i+1、i+2和i+3上的虚拟流体状态及网 格 点i上 的真实流体 状 态,上述即给定 了 气体的界面边界条件。对于水可进行类似操作,同样的,虚拟点上的密度都为水的密度。

上述2种方法给出了水和气体的界面边界条件,在这个基础上,分别采用不同的离散方法求解水和气的控制方程,并通过求解level set方程更新level set函数隐式追踪界面。

图2 利用RGFM方法对气体定义界面边界条件Fig.2 The definition of interface boundary condition for gas by RGFM method

3 数值模拟

对一维水/气多介质问题进行数值模拟,时间方向上采用三阶 TVD Runge-Kutta方法,空间上用三阶ENO格式离散欧拉方程组,对于不可压方程组采用标准的二阶投影算法离散求解。

3.1 水在空气中高速运动

在长度为1 m,网格点为200的区域内,中心处有长度为0.2 m 的水被周围的静止的气体包围,其中气 体 的 状 态 为γ=1.4,ρ=1.226 kg/m3,u=0,p=100 kPa,水 的 状 态 为ρ=1 000 kg/m3,u= 100 m/s,p=100 k Pa。水在静止的空气中突然以一定速度向右运动,导致水右侧的气体中产生激波,在水的左侧气体中产生稀疏波。图3~6所示为在时间t=0.75 ms时,利用 MGFM 和 RGFM 和 newGFM 这3种方法[1]计算得到的流场状态结果对比图。

由图3~6中可以看出,3种方法都能较准确地捕捉到界面和激波的位置,在激波处,由于密度变化过小而很难在图中体现。3种方法计算结果对于界面位置的捕捉结果基本相同,这是由于水/气 Riemann问题的解给出的界面处的速度为界面附近水的速度,这一结论与new GFM 方法中界面的速度直接取界面附近水的速度相同。而 MGFM 方法和 RGFM 方法计算结果中,激波位置比new GFM 方法领先1个网格步长,这是由于界面处的压力是由水/气 Riemann问题得到,没有简单的取界面附近的气体的压力,充分考虑了界面两侧水/气物质属性差异对界面处流动状态的非线性影响。此外,通过网格加密方法对 RGFM 方法进行了收敛速度测试,在200、400 和 800 个网格点上计算得到在时间t= 0.75 ms时水的速度依次为99.693、99.689 和 99.687 m/s,计算得到收敛速度为0.992 7。

图3 密度1 000 kg/m3的水在空气中向右运动时流场密度Fig.3 Density profile of the water movement in air while water density is 1 000 kg/m3

图4 密度1 000 kg/m3的水在空气中向右运动时流场速度Fig.4 Velocity profile of the water movement in air while water density is 1 000 kg/m3

图5 密度1 000 kg/m3的水在空气中向右运动时流场压力Fig.5 Pressure profile of the water movement in air while water density is 1 000 kg/m3

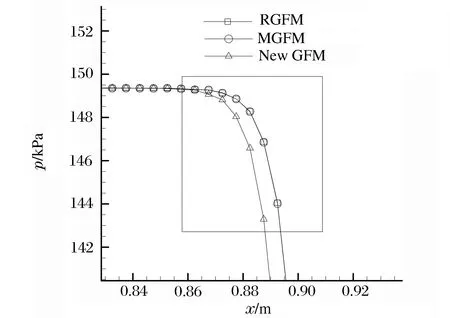
图6 流场压力细节对比图Fig.6 Detail comparison of pressure profile

为了进一步考察水的密度对于计算结果的影响,将上述算例中的水密度变为10 kg/m3,图7~10给出了在时间t=0.75 ms时,3种方法得到的计算结果对比。

对于界面位置的捕捉,3种方法计算的结果基本相同,在激波处,密度变化明显可以分辨。由于水的密度变小,更容易被空气减慢速度,使得在水与右侧的激波间,和水与左侧的稀疏波之间都产生1个二次稀疏波。在这2个二次稀疏波中,new GFM 方法计算结果的速度大于 RGFM 和 MGFM 方法的计算结果,激波位置落后1个网格步长,MGFM 和 RGFM 方法只在稀疏波区域有细微差异,在区域其他点上基本相同。利用网格加密方法对 RGFM 方法进行收敛速度测试,在200、400和800个网格点上计算得在t=0.75 ms时,水的速度分别为73.589、73.315和73.171 m/s,计算出收敛速度为0.953 1。

3.2 激波与水/气界面相互作用

图7 密度10 kg/m3的水在空气中向右运动时流场密度Fig.7 Density profile of the water movement in air while water density is 10 kg/m3

图8 密度10 kg/m3的水在空气中向右运动时流场速度Fig.8 Velocity profile of the water movement in air while water density is 10 kg/m3

图9 密度10 kg/m3的水在空气中向右运动时流场压力Fig.9 Pressure profile of the water movement in airwhile water density is 10 kg/m3

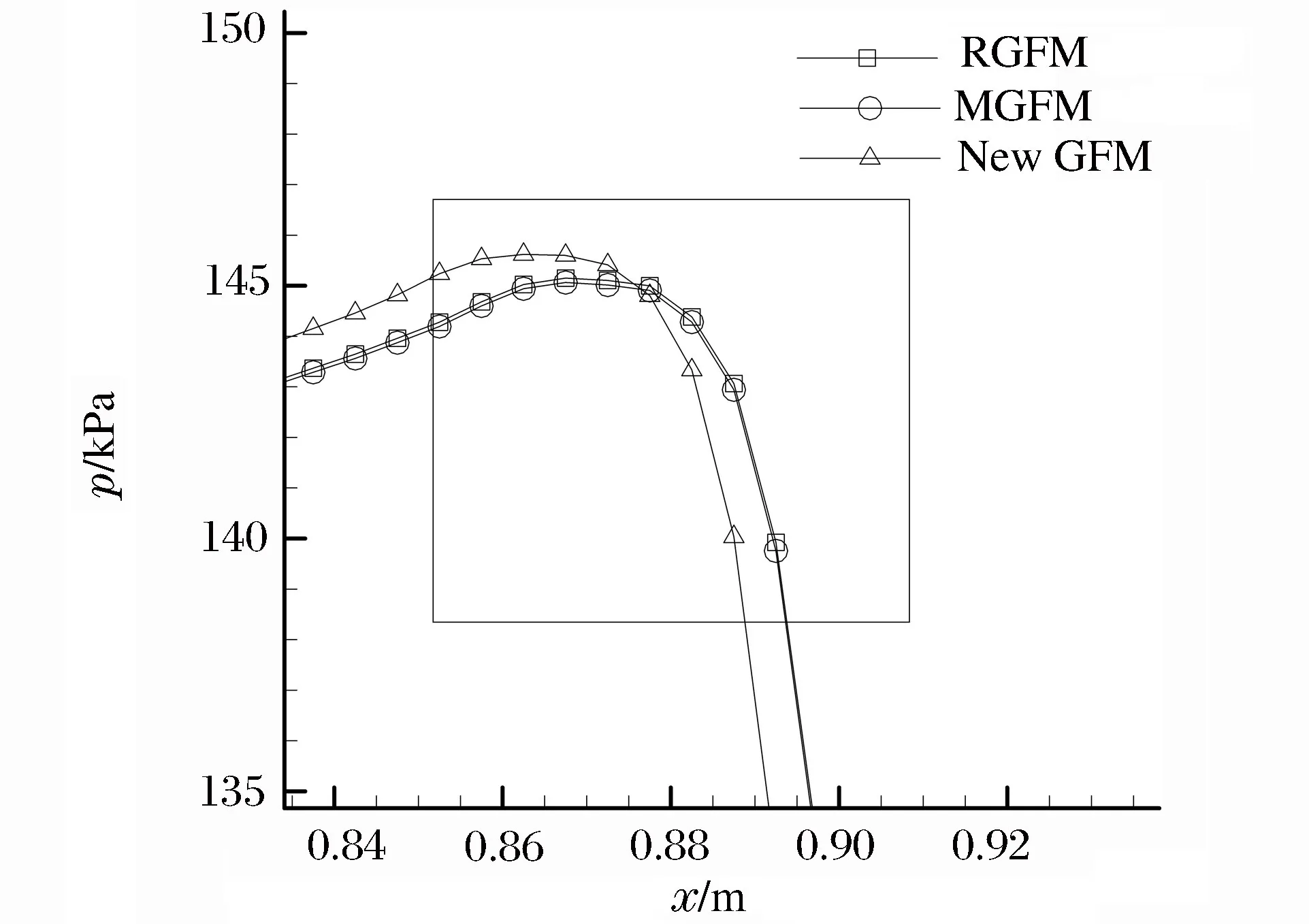
图10 流场压力细节对比图Fig.10 Detail comparison of pressure profile

在长度为1 m,网格数 为200 的区域 内,有 状 态 为ρ=1 000 kg/m3,u=0,p=98.067 k Pa,长 度 为0.2 m的 水 在 区 域 中 心 ,周 围 的 空 气 状 态 为ρ=1.58 kg/m3,u=0,p=98.067 kPa,在0.1 m 处 的 空 气 中有一向右运动的激波,其 中波 后 状 态 为ρ=2.124 kg/m3,u=89.98 m/s,p=148.407 k Pa。 图 11~14所示为在时间t=1.75 ms时,分别采用 MGFM、RGFM 和 new GFM 这3种方法的激波与水/气界面相互作用的计算结果对比图。激波与水/气界面相互作用时,由于水的刚性很强会产生1个反射激波,和1个很弱的入射波,入射波以极快的速度穿过水的区域,进入右侧的空气,入射波由于强度太小而很难在图中分辨。MGFM 和 RGFM 方法的计算结果中,激波的位置领先new GFM 方法中激波位置1个网格步长。由于入射波的作用,水滴产生1个向右的速度,同时由于水密度较大,导致产生的速度过小。通过网格加密方法对 RGFM 方法进行收敛速度测试,在200、400和800个网格点上计算得到在时间t=1.75 ms时水的速度分别为0.531、0.538和0.542 m/s,计算得到收敛速度为0.9835。

将上述算例中的水密度变为ρ=10 kg/m3,图15~18所示为采用3种方法计算得到结果对比图。由结果可以看出,激波与水/气界面相互作用以后,产生1个向左的反射激波,在这个反射激波与水之间形成了1个二次稀疏波,于此同时,向右运动的入射波以极快的速度穿过水进入右侧的气体中形成一个稀疏波,这一结果也符合波在水中的传播速度无穷大的性质。

图12 水密度1 000 kg/m3时激波与水/气界面相互作用后的流场速度Fig.12 Velocity profile of shock impact with water-gas interface while water density is 1 000 kg/m3

图13 水密度1 000 kg/m3时激波与水/气界面相互作用后的流场压力Fig.13 Pressure profile of shock impact with water-gas interface while water density is 1 000 kg/m3

图14 流场压力细节对比图Fig.14 Detail comparison of pressure profile

图15 水密度10 kg/m3时激波与水/气界面相互作用后的流场密度Fig.15 Density profile of shock impact with water-gas interface while water density is 10 kg/m3

图16 水密度10 kg/m3时激波与水/气界面相互作用后的流场速度Fig.16 Velocity profile of shock impact with water-gas interface while water density is 10 kg/m3

由图15~18中的对比结果可知,在激波位置方面,MGFM 和 RGFM 方法的计算结果仍然比new GFM 方法的计算结果要领先,在二次稀疏波范围内,new GFM 方法的计算结果中,速度比另两种方法的结果稍小,而压力比另外2种方法的结果大。

由于 RGFM 方法中,不仅用 Riemann问题的解定义了界面处虚拟点的状态值,同时也修改了界面处真实流体的速度和压力,而 MGFM 方法中,只是修改了虚拟流体点的速度和压力,对于界面处真实流体点只是通过等熵修正了密度,并没有修改压力和速度,因此在得到的结果中,RGFM 方法中水的速度相对另外两种方法要略大。通过网格加密方法对 RGFM 方法进行了收敛速度测试,在200、400和800个网格点上计算得到在时间t=1.75 ms时水的速度分别为40.117、40.431和40.589 m/s,计算得到收敛速度为0.9922。

图17 水密度10 kg/m3时激波与水/气界面相互作用后的流场压力Fig.17 Pressure profile of shock impact with water-gas interface while water density is 10 kg/m3

图18 流场压力细节对比图Fig.18 Detail comparison of pressure profile

4 结 论

针对水/气多介质问题,考虑将水作为不可压流体,气体作为可压缩流体,在基于不可压无黏流体是可压缩流体在马赫数趋向于零的收敛极限的结论上,定义并求解了水/气 Riemann问题,Riemann问题的解反映出界面处真实的流动状态,并采用 MGFM 以及RGFM 这2种方法给出了更合理的反应水/气物质属性差异的界面边界条件。通过一维数值算例结果以及与相应的new GFM 方法计算结果的对比分析,证明了算法的有效性及合理性,同时对 RGFM 方法进行了收敛速度测试,充分考虑了水的不可压缩性质以及气体的可压缩性质,适合针对水/气具有不同的运动特性的水/气多介质问题,例如空气处于高速运动或者有强激波存在而水处于低速运动状态,此时不能被忽略水的不可压性质,同样的适合于需要考虑水中波的传播速度等问题,如水下爆炸。

[1]Caiden R,Fedkiw R P,Anderson C.A numerical method for two-phase flow consisting of separate compressible and incompressible regionsg[J].Journal of Computational Physics,2001,166(1):1-27.

[2]Fedkiw R P,Aslam T,Merriman B,et al.A non-oscillatory Eulerian approach to interfaces in multimaterial flows:The ghost fluid method[J].Journal of Computational Physics,1999,152(2):457-492.

[3]Liu T G,Khoo B C,Yeo K S.Ghost fluid method for strong shock impacting on material interface[J].Journal of Computational Physics,2003,190(2):651-681.

[4]Liu T G,Khoo B C,Wang C W.The ghost fluid method for gas-water simulation[J].Journal of Computational Physics,2005,204(1):193-221.

[5]Wang C W,Liu T G,Khoo B C.A real ghost fluid method for the simulation of multimedium compressible flow [J].SIAM Journal on Scientific Computing,2006,28(1):278-302.

[6]王春 武,赵 宁.基于求 解 Riemann问题的界面 处理方法[J].计算物理 ,2006,22(4):306-310. Wang Chun-wu,Zhao Ning.An interface treating method based on Riemann problems[J].Chinese Journal of Computational Physics,2006,22(4):306-310.

[7]Agemi R.The incompressible limit of compressible fluid motion in a bounded domain[C]∥Proceedings of the Japan Academy Series A:Mathematical Sciences.1981.

[8]Steve S.The compressible Euler equations in a bounded domain:Existence of solutions and the incompressible limit [J].Communications in Mathematical Physics,1986,104(1):49-75.

[9]Asano K.On the incompressible limit of the compressible Euler equation[J].Japan Journal of Applied Mathematics,1987,4(3):455-488.

[10]Jiang G S,Shu C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996,126(1):202-228.

Interface treating methods for the gas-water multi-phase flows

Xu Shuang1,Zhao Ning1,Wang Chun-wu2,Wang Dong-hong2
(1.College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics, Nanjing 210016,Jiangsu,China;
2 College of Science,Nanjing University of Aeronautics and Astronautics, Nanjing 210016,Jiangsu,China)

A new interface treating method is presented for the compressible-incompressible gas-water multi-phase flow.The Riemann problem is constructed at the compressible gas-water interface,and then solved according to the hypothesis that the sound speed tends to infinity in the water.The solution of Riemann problem provides the fluid states for compressible gas and incompressible water at the interface.Those states can then be used to define the interface boundary condition by coupling the ghost fluid method.The level set method is employed to track the interface.The numerical examples of one-dimension case are given in this paper,furthermore,several comparisons are made with other results to verify the algorithm.Numerical results show that the provided algorithm can capture the discontinuities accurately,which demonstrates the robustness and efficiency.

mechanics of explosion;Riemann problem;ghost fluid method;level set;gas-water interface;multi-phase flows

O382.1国标学科代码:13035

:A

10.11883/1001-1455-(2015)03-0326-09

(责任编辑 王易难)

2013-11-14;

2014-02-28

国家 自然科学基 金项目(11271188,91130030);北京理工大学爆炸科学与技术国家重点实验室开放基金项目(KFJJ11-4 M)

徐 爽(1984— ),男,博士研 究生,shuangxu@nuaa.edu.cn。