强爆炸早期火球光辐射能谱的数值计算*

高银军,闫 凯,田 宙,刘 峰

(西北核技术研究所,陕西 西安710024)

强爆炸早期火球光辐射能谱的数值计算*

高银军,闫 凯,田 宙,刘 峰

(西北核技术研究所,陕西 西安710024)

基于强爆炸火球光辐射的多群辐射流体力学方法,采用算子分裂方法将方程组分裂为对流项和刚性源项,其中源项部分根据方程形式,进一步分裂为各群内的单独求解。数值计算表明:该方法克服了直接求解过程中辐射与流体耦合所带来的强不稳定性,时间步长大幅提高,给出的火球光辐射能谱特征与已有规律一致。可为定量分析光辐射能谱特征提供有效手段。

爆炸力学;算子分裂算法;光辐射能谱;强爆炸火球

在强爆炸过程中,由于强爆炸所释放的巨大能量迅速加热周围冷空气,从而形成高温高压的火球。火球在发展过程中,不断向外辐射光和热,称为光辐射(也称为热辐射)。光辐射是强爆炸的重要毁伤效应之一,研究其能谱特征对于深入分析光辐射与物质相互作用、评估相应的毁伤效应具有重要意义[1]。

强爆炸火球光辐射是一个涵盖近紫外到可见光直至远红外的宽谱带,同时伴随火球的发展变化过程呈现不同的特征。早期的研究是基于实验测量,结合相应的理论分析,给出了光辐射各谱段较为接近的经验公式[1-2]。随着 相关理 论及数 值模拟 研究的 发 展,特 别 是 对 火 球 发 展 过 程 的 深 入 分 析,较 普 遍 认为采用灰体近 似下的 辐射流 体力学 方法可 以较好 的描述 火球发 展过程[3-7],并 给出了 光辐射 总能 量 的 时空分布规律[8-11]。但是灰体近似在处 理 光 辐 射 输 运 过 程 中 ,假 定 辐 射 系 数 (空 气 吸 收 系 数 )与 光 子 能 量无关,采用全谱范围内的平均计算,因而无法给出光辐射能谱特征。

为能够给出光辐射能谱,需采用多群方法,即在不同能谱范围内求解光辐射输运过程,分群越多,计算得到光辐射能谱特征越精细[12]。显 然,这 种 处 理 方 法 的 代 价 使 得 辐 射 方 程 的 计 算 更 为 复 杂 ,需 要 辐射参数(分群吸收系数)更多,与流体耦合后求解,更容易由于方程的强非线性、强刚性[2](尤其是辐流耦合项)而 出 现 计 算 不 稳 定(除 非 将 时 间 步 长 限 制 非 常 小)。 国 外 有 关 文 献[4,12]仅 给 出 了 部 分 结 果 ,但 并 未涉及方程求解 中的具 体 处 理 过 程。 国 内 光 辐 射 能 谱 方 面 的 计 算 较 少,早 期 计 算[13]中 利 用 小 步 长 (约10-15s)直接求解的方法,给出了光辐射较短时间内的能量分布情况。

本文中基于辐射流体力学方法,采用多群方法求解光辐射输运过程。方程求解过程中,为克服方程的强非线性、辐流耦合项的强刚性可能产生的计算不稳定问题,通过算子分裂方法,将多群方程逐步分裂为对流项和源项单独求解[14-15],其中源项部分 的求解需要在各群内进一步分裂,使之具 有单群 方程的形式。在这样的处理方法下,多群辐流方程的求解比直接求解更稳定,即使在大时间步长(约10-11s)下也能得到较好的结果,有效提高了计算效率,为大规模问题求解提供了条件。利用该计算方法,计算得到了强爆炸早期光辐射能谱特征分布,与经验关系给出的规律较为一致,为定量分析光辐射能谱特征提供了有效手段。

1 计算方程及参数

在局域热动力平衡(LTE)假定下,描述强爆炸火球光辐射发展的多群辐射流体力学方程如下:

式(1)~(3)分 别 为 质 量 守 恒 、动 量 守 恒 和 能 量 守 恒 方 程 。 式 中 :ρ为 空 气 密 度 ,v为 空 气 速 度 ,p为 空 气压 力 ,e为 空 气 内 能 。为 各 群 内 光 辐 射 输 运 的 总 动 量为各 群 内 光 辐 射 输 运 的 总 能 量,上 标 “0”和 “1”表 示 辐 射 输 运 方 程 的0阶矩 和1阶 矩 方 程,下 标g=1,2,3… 即 分 群 数 目 ,分别为第g群辐射能密度、辐射能流、辐射压力张量及光辐射输运能量和光辐射输运动量。具体计算如下:

式 中 :c为 光 速 ,κg为 第g 群 吸 收 系 数 ,γ为 光 子 频 率 。 由 于 各 群 光 子 能 量 具 有 上 限 和 下 限 ,因 此 采 用γg、γg-1分 别 标 记 第g群 光 子 频 率 的 上 限 和 下 限 。E(γ),F(γ)及P(γ)分 别 为 辐 射 能 密 度 、辐 射 能 流 及辐 射 压 强 张 量 函 数,与关 系 为为 黑 体 辐 射 谱 分 布 ,h为 普 朗 克 常 数 ,k为 波 尔 兹 曼 常 数 ,Bg为 黑 体 辐 射 下 第g 群 辐 射 能 密 度 :

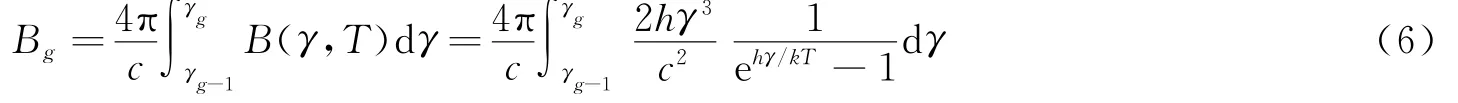
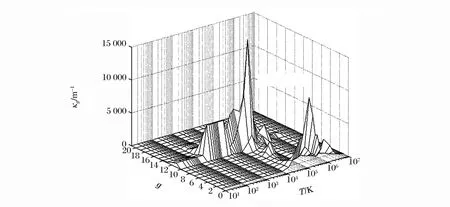
图1 吸收系数与光子能量(分群)和温度关系Fig.1 Absorption coefficient of air varied with the temperature and photon energy

吸收系数采用文献[17-18]给出的21群 Rosseland分群吸收系数κg。多群方法下,吸收系数为空气温度、密度以及光子分群能量的函数。数值求解中,通过双线性插值计算相应的温度、密度下,空气的分群吸收系数。图1给出空气密度为,分群吸收系数与光子能量(分群)和温度的关系。

对 于 各 群 内 分 群 辐 射 压 强 张 量Pg,采 用 最 大 熵 变 Eddington 因 子 近进 行 计 算 ,空 气 的 状 态方 程 采 用 实 际 空 气 状 态 方。 光 辐 射 按 照 对 应 的 光 子 能 量pe分 为 21,如 表 1 所 示 。

表1 光子分群能量Table 1 Photon energy of each group

2 数值求解

2.1 分裂方法过程

一维球对称下多群辐流方程组展开后也可写成如下矩阵形式:

各项代表的物理量如下:

式中:Ψ为对流项,Φ为辐射与流体耦合项,即刚性源项部分。利用算子分裂方法,将方程分2步求解:

第1步求解对流项,采用有限体积法,构造五阶 WENO 格式,数值通量的计算采用局部 Lax-Friedrichs方法,由于不 含刚性 源项,因而时间步长可以提高到10-11s,相比于直接法求解[13],极 大提高了计算效率。第2步求解源项,其初始 时刻(t=t0)的值 为第1 步对流 项方程 的解f(1)*。 源 项 求 解 较为复杂,首先根据方程特征,写为:

分裂成为这样的步骤进行求解,方程形式大为简化,其过程本身也具有自身的物理意义:每步求解认为流体仅与该群光子进行能量和动量交换,二者组成的体系中,总能量和总动量守恒。这样的假设,在方程分裂的数学处理过程中是严格满足的:因为其他群内辐射能密度与辐射能流随时间的微分都等于0。进一步的求解,则转化为常微分方程组的求解,可以通过多种方法实现快速、高精度求解。

2.2 初始条件和边界条件

求解初始条件假定爆炸总能量集中于等压火球内,辐射能与空气内能总合等于爆炸总能量,计算边界条件采用对称边界。光辐射分群能量的初始分布通过Bg给出,分群辐射能流为0。

在数值求解中,计算区域的边界处,假定物理量都处于未扰动状态,即认为:流体速度以及辐射能流均为0,而其他状态参量取初始值。

3 计算结果与分析

取当量为1 kt,高度在海平面(h=0 km),求解相应的强爆炸火球光辐射输运过程,空气初始状态参量如表2所示。

表2 不同高度空气初始状态参数Table 2 Air state parameters at different altitude

强爆炸火球发展过程中,冲击波阵面和辐射波阵面是一个描述火球发展的重要参量。利用上述算子分裂方法计算得到的强爆炸火球阵面走时,如图2所示,符合火球发展的物理过程,与 H.L.Brode[4]计算的结果符合较好,说明该方法在处理过程中是稳定可靠的。

图2 算子分裂法求解多群辐流方程组得到的早期火球阵面走时Fig.2 Calculational result of 1 kt nuclear fireball front by splitting method

多群方法的运用,能够给出火球光辐射在特定时刻向外辐射的光辐射能谱特征。图3所示为t=0.023 s时 刻 火 球 光 辐 射 分 群 (21 群)能 量 分布,I为光辐射强度。从图3中可以看出,火球光辐射能量集中于第2~8群,对应光子波长在0.2 ~2μm。

根据火球发展过程,在光辐射强度第1个极大 值 后,火 球 有 效 温 度 从 约 20 000 K 降 低 至3 000 K,在 光 辐 射 强 度 第2个 极 大 值 时,火 球 有效 温 度 略 低 于10 000 K。 在 这 个 温 度 范 围 内,火球光辐射能谱大部分能量都集中与紫外(0.22~ 0.36μm)、可见(0.36~0.64μm)和红外(0.64~ 4.5μm)部分,与图3所示基本一致。

为具体分析火球光辐射能谱特征,利用文献[1-2]给出的火球有效温度走时关系:

图3 光辐射分群能谱Fig.3 Fireball radiation energy of each group

式 中 :Te为 火 球 有 效 温 度 ,σ为 斯 特 潘-玻 尔 兹 曼 常 数 ,Φe为 与 火 球 辐 射 功 率 有 关 的 函 数 表 达 式 ,r为 火球半径,各个参数可以通过已有规律计算给出。以t=0.01、0.02 s时刻为例,利用上述理论方法计算得到该爆炸条件下火球有效温度约为3 500K 和7 453 K,据此给出0.01~2.5μm 波长范围内光辐射强度随波长关系与对应有效温度下的黑体谱对比分析,如图4所示,图中实线为本文中方法的计算结果,虚线为由文献理论计算的黑体谱分布。

已 有 研 究 结 果 表 明[1-2],在 火 球 光 辐 射 强 度 第 1 个 极 大 值 后 的 整 个 发 光 阶 段,波 长 在 (0.4~ 0.6μm)范围内,可以近似看做黑体,与图4给出的结果在变化规律上基本一致,数值大小上的差异,与所采用的空气吸收系数等有关,需要进一步工作进行细致改进。

图4 不同时刻光辐射强度与波长变化关系Fig.4 Relation between intensity of fireball radiation and wavelength

4 结 论

(1)基于强爆炸火球的多群辐射流体力学模型,采用算子分裂方法对方程组进行数值求解。利用空气分群(21群)吸收系数,计算给出了1 k T 当量下火球光辐射能谱特征。数值计算结果验证了光辐射能谱主要集中在0.2~2μm(紫外、可见到红外波段),与已有结果和经验规律符合的较为一致;

(2)分裂求解的处理方法,一方面克服了直接求解过程中辐射与流体耦合可能带来的强不稳定性,另一方面扩大了时间步长,提高了计算效率,为类似方程的数值求解提供了一定借鉴。

[1]乔 登 江 .核 爆 炸 物 理 概 论 [M].北 京:国 防 工 业 出 版 社,2003:225-262.

[2]屠 琴 芬 .核 爆 炸 火 球 的 辐 射 流 体 力 学 计 算 中 的 几 个 问 题[R].西 安:西 北 核 技 术 研 究 所 ,1986.

[3]Pomraning G C.The equations of radiation hydrodynamics[J].Astrophysical Radiation Hydrodynamics,1986 (188):45-69.

[4]Brode H L.Fireball phenomenology[R].AD0612197,1964.

[5]Crowley B K,Glenn H D,Marks R E.An analysis of marvel:A nuclear shock-tube experiment[J].Journal of Geophysical Research,1971,76(14):3356-3374.

[6]Marrs R E,Moss W C,Whitlock B.Thermal radiation from nuclear detonations in urban environments[R]. UCRL-TR-231593,2007.

[7]Lowrie R B,Edwards J D.Radiative shock solutions with grey nonequilibrium diffusion[J].Shock Waves,2008, 18(2):129-143.

[8]陈 健 华 ,王 心 正,谢 龙 生 ,等.均 匀 大 气 中 的 强 爆 炸 一 维 辐 射 流 体 力 学 数 值 解[J].爆 炸 与 冲 击 ,1981,1(2):37-49. Chen Jian-hua,Wang Xin-zheng,Xie Long-sheng,et al.A one-dimensional radiation hydrodynamic numerical solution for a strong explosion in uniform atmosphere[J].Explosion and Shock Waves,1981,1(2):37-49.

[9]田 宙 , 乔 登 江 ,郭 永 辉 . 不 同 当 量 强 爆 炸 早 期 火 球 现 象 的 数 值 模 拟[J].爆 炸 与 冲 击 ,2009,29(4):408-412.Tian Zhou,Qiao Deng-jiang,Guo Yong-hui.Numerical simulation on early fireball phenomenology of strong explosions for different yields[J].Explosion and Shock Waves,2009,29(4):408-412.

[10]田 宙,乔 登江 ,郭永 辉.不同高 度强爆炸早 期火球数值 研究[J].兵 工学 报,2009,30(8):1078-1083. Tian Zhou,Qiao Deng-jiang,Guo Yong-hui.Numerical investigation of early fireball of strong explosion for different altitudes[J].Acta Armamentarii,2009,30(8):1078-1083.

[11]田 宙,乔 登江 ,郭永 辉.强爆炸 早期火球现 象的一维数 值研究[J].计算 物理,2010,27(1):9-14. Tian Zhou,Qiao Deng-jiang,Guo Yong-hui.A one dimensional numerical study on early fireball in strong explosion[J].Chinese Journal of Computational Physics,2010,27(1):9-14.

[12]Symbalisty E M D,Zinn J,Whitaker R W.Radflo physics and algorithms[R].LA-12988-MS,1995.

[13]高 银军,田宙 ,刘峰 ,等 .强爆 炸早期火球 光辐射能谱 的分群计算[J].四川兵 工学 报,2011,32(3):21-24. Gao Yin-jun,Tian Zhou,Liu Feng,et al.Calculation of energy spectrum of early fireball radiation in strong explosion with multi-group method[J].Journal of Sichuan Ordnance,2011,32(3):21-24.

[14]闫 凯.二 维辐 射流体 动力学方程 组的数值求 解[D].西安 :西北核技 术研究所,2011.

[15]闫 凯.二 维辐 射流体 动力学方程 组的数值求 解[C]∥第六届 全国青年计 算物理学术 会议.太原 ,2011.

[16]Minerbo G N.Maximum entropy eddington factors[J].Journal of Quantitative Spectroscopy and Radiative Transfer,1977,20(6):541-545.

[17]王 文高,张建 泉.物 质辐射不透 明性Ⅰ[R].西 安:西北核 技术研究所 ,1978.

[18]王 文高,张建 泉.物 质辐射不透 明性Ⅱ[R].西 安:西北核 技术研究所 ,1978.

Numerical calculation of early fireball radiation spectrum in strong explosion

Gao Yin-jun,Yan Kai,Tian Zhou,Liu Feng
(Northwest Institute of Nuclear Technology,Xi’an 710024,Shaanxi,China)

On the basis of multi-group radiation hydrodynamics method of fireball radiation in strong explosion,operator splitting method is used to split the equations into convection items and source items,which are split into radiation groups due to the equation formation and solved individually.Numerical calculations show that the method used here overcomes strong instability when solving the equations directly because of the coupling items between radiation and fluid.In the meantime,the time step in the calculation is increased obviously.Fireball radiation spectrum is obtained in fine accordance with the result in the literature.

mechanics of explosion;splitting method;radiation spectrum;strong explosion fireball

O381国标学科代码:13035

:A

10.11883/1001-1455-(2015)03-0289-07

(责任编辑 王易难)

2013-03-13;

2013-05-31

高银 军(1983— ),男,硕士研 究生,助理 研究员,gyj@mail.ustc.edu.cn。