爆炸容器内小药量实验动态标定压力传感器*
薛 冰,马宏昊,沈兆武,余 勇
(中国科学技术大学近代力学系,安徽 合肥 230026)
爆炸容器内小药量实验动态标定压力传感器*
薛 冰,马宏昊,沈兆武,余 勇
(中国科学技术大学近代力学系,安徽 合肥 230026)
在爆炸容器中进行小药量空中爆炸实验,利用传感器序列测量冲击波速度,根据冲击波 Rankine-Hugoniot关系获得测点近似理论峰值压力,从而实现压力传感器的标定,获得的灵敏度相对误差较小。同时测量了相应的冲击波参数,并利用 Modified-Friedlander公式进行数据后处理,结果表明固定超压拟合更接 近物理事实,固定正相时间拟合也具有较高精度。最后进行了误差分析,发现不同传感器特性及数据后处理方法都会带来一定误差。实验结果表明这种测量和后处理方法具有较高的精度,可以同时标定传感器和测量冲击波参数。
爆炸力学;动态标定;空中爆炸;压力传感器;爆炸容器;冲击波;传感器序列
空中爆炸实验通常以大药量、自由场实验为主,但自由场爆炸实验成本以及对实验场地的要求均较高。在爆炸容器内进行小药量实验精度要求高,但所需场地小,数据重复性好,能经济有效地测试炸药的空中爆炸参数,在实验场地等条件受限时是一个有效的测试方法。根据爆炸相似律可以将实验结果推广,满足一定范围内使用需求。在空中爆炸冲击波参数实验测量中,超压峰值、正相时间和正相冲量是反映冲击波强度和炸药性能的主要参数。而空中爆炸冲击波的传播对实验环境条件极为敏感。冲击波激发测试系统固有频率的震荡、爆炸破片对传感器和流场可能的干扰以及爆炸容器内存在的壁面反射等因素,都会给冲击波参数的 测量带来较大影响。为了准确获得冲击波参数,N.H.Ethridge[1]提 出了一种基于 Modified-Friedlander方程的 半 对 数 线 性 拟 合 处 理 方 式。 M.M.Ismail等[2]利 用 这 种 经 验的半对数线性拟合对空中爆炸实验数据处理进 行 了 研 究,并 在 G.F.Kinney等[3]工 作的基础上进 行 了修正。但是,由于这种处理方式在数据选取时主观性较强,很难得到客观的结果。在实际应用中,半对数线性近似的爆炸冲击波衰减初期的时间范围很难确定,范围较大则不满足近似的前提,范围过小则容易受到传感器性能的影响而使结果失真。因此,需要一种更客观的数据处理方式,减少人为因素。本文中,提出一种基于小药量空中爆炸冲击波实验、利用传感器序列测量冲击波速度、根据冲击波 Rankine-Hugoniot关系获得测点近似理论峰值压力的方法,对压力传感器进行动态标定,讨论测量误差的来源,给出相应的爆炸冲击波参数后处理方法。
1 传感器动态标定
使用前需对压力传感器进行标定,张元平等[4]提出了一种基于经验公式的动态标定方法,但是该方法对文献数据依赖较强,不能很好地处理实际实验误差。为了同时实现压力测量和动态标定,利用传感器序列连续测量获得冲击波通过一定距离所需时间,采用线性近似计算,可以得到测点处激波马赫数:
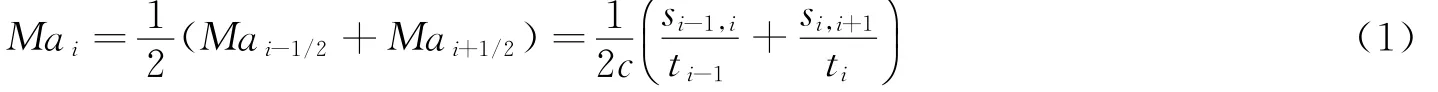
式 中 :Mai为 测 点i处 爆 炸 冲 击 波 的 马 赫 数 ;c为 波 前 声 速 ,c=γRT;s为 相 邻 测 点 间 的 距 离 ;ti为 冲 击波通过相邻测点的时间间隔。
利用冲击波 Rankine-Hugoniot关系式:

可以对相应测点的压力进行计算,结合传感器电压信号可对相应传感器进行动态标定。式中:pi为测点i处 的 绝 对 压 力 ;p0为 环 境 压 力 ;γ为 空 气 比 热 比 ,在 低 马 赫 数 下 ,γ=1.4。
为了验证这种方法的可行性和精度,利用未标定传感器序列和已标定压力传感器在爆炸容器内进行相应实验测量。未标定传感器敏感面直径为6 mm,被依次安装在半圆柱外壳内,传感器敏感面与外壳平面保持水平,以保证冲击波成掠入射,相邻传 感 器 中 心 距 离 为 :s1,2=9.60 mm,s2,3= 12.60 mm。传感器序列装置如图1所示。

图1 传感器序列示意图Fig.1 Schematic of sensor series assembly
所 有 传 感 器 外 壳 均 安 装 在 半 径R=1.25 m 的空中爆炸容器中。传感器敏感面正对装药中心,未标定传感器2和已标定传感器距离装药中心距离R1=0.7 m。 实 验 装 药 为10 g钝 化 黑 索 金 压 装 药柱,无外壳,采用飞片式无起爆药雷管起爆。实验数据由数 字 示 波 器 采 集,采 样 率 为2×107s-1。 实 验装置示意如图2所示。
通过空中爆炸实验得到每个传感器的压力时程曲线,由传感器序列中每个传感器的冲击波到达时间,可以得到冲击波经过相邻传感器所需时间。在已知传感器间距离时,可以利用公式(1)计算得到冲击波经过相邻传感器时的平均马赫数。图3所示为传感器序列采集到的冲击波信号的到达时间。

图2 空中爆炸实验装置示意图Fig.2 Schematic of air explosion system
由于离爆心较远,此时的冲击波马赫数较低,衰减较缓慢,且相邻传感器间距离很小,因此可以认为冲击波速度在测试区域为线性衰减。对于本次实验传感器间距不相等的情况则需要线性插值。实验结果见表1,表中k为传感器灵敏度,Δpm为超压峰值,U为电压。
利用冲击波速度计算得到的超压峰值相对误差为1.42%,最终计算得到的传感器灵敏度相对误差为0.7%。实验结果表明,利用传感器序列计算得到的冲击波超压峰值能够有效地标定传感器。如果采用多个传感器组成序列,则可以同时标定多个传感器,并提高冲击波速度计算精度。

图3 冲击波到达传感器序列的时间Fig.3 Arrival time of shock wave at sensor series

表1 传感器2动态标定结果Table 1 Dynamic calibration results of sensor 2
2 冲击波参数测量及后处理
采用掠入射式压力传感器测量空中爆炸冲击波参数,能直接获得测点的压力时程曲线,从而获得冲击波超压、正相时间和正相冲量等参数。并且这种方式对流场干扰较小,可以实现多点测量。前面实验中,在动态标定传感器的同时测量了相应的冲击波参数。炸药空中爆炸冲击波测试是在多破片、强振动冲击、瞬态高温、强电磁的恶劣环境下进行的。冲击波信号成份复杂,使得冲击波超压峰值、正相时间、比冲量等原始数据不理想,数据处理方法不当,会直接影响测量结果[5]。为了获得更准确的爆炸冲击波参数,本文中提出基于 Modified-Friedlander方程:

的全数据段拟合方法,即对原始数据正压区全部下降沿进行拟合,以减小半对数线性拟合时的人为干扰 。 式 中 :p为 测 点 处 绝 对 压 力 ;p0为 环 境 压 力 ;t为 超 压 时 间 历 程 ;Δpm为 超 压 峰 值 ;t+为 冲 击 波 正 相时间;α为波形系数,反映冲击波衰减的快慢。
Modified-Friedlander方程是一个3参数的拟合式,是空中爆炸冲击波正压区常用的拟合形式。但由于空中爆炸冲击波的超压峰值Δpm和正相时间t+数量级相差较大,最小二乘法拟合时矩阵条件数很大,导致不可解的病态矩阵,因此不可能对3个参数同时进行拟合,而需要提前确定一个参数,拟合另外2个参数[6]。冲击波衰减波形系数α无法提前确定,因此有2种拟合方式:方法1,在拟合之前利用传感器序列测定的冲击波速度计算确定 Δpm,在拟合时则只需要确定t+和α;方法2,在拟合之前利用原始数据确定冲击波正相时间t+,在拟合时确定Δpm和α。
在超压时程曲线拟合完后,利用下式可以计算冲击波正相冲量:

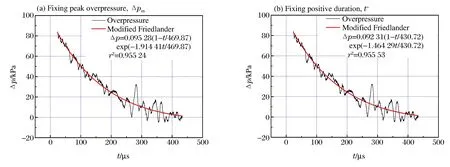
图4 超压时程曲线拟合Fig.4 Nonlinear curve fit of overpressure history traces
对传感器2采集到的数据按照上述2种方法进行处理,结果见图4,已标定传感器的原始压力时程曲线见图5。利用不同方法处理数据得到的冲击波参数,见表2,表中实验对应的参数为标准传感器直接读取的参数。由于实验传感器2下降沿后段出现振荡无法准确确定正相时间,因此在固定正相时间拟合时取用标准传感器的正相时间。
实验标准传感器测得的数据重复性较好,超压峰值和正相时间相对误差小于2%,由于空中爆炸压力测量受到到传感器时间—空间平均等效应的影响,测 量 值与实际值之 间 存 在偏差[7]。与利用冲 击 波速度计算得到冲击波超压相比,直接测量值约小10%。2种拟合方法的数据处理结果表明,这种对整个正相超压时程曲线进行拟合的方法能够很好地反映冲击波曲线的特点,并且消除干扰信号对冲击波参数确定的影响,比如曲线后段出现的由于传感器固定装置自振引起的干扰得到了很好的消除。
方法1固定的超压具有一定物理依据,因此拟合方程更能反映真实冲击波参数,但需要传感器序列测量超压,实验系统相对复杂。方法2由于只能通过原始数据判读正相时间来拟合,因此会受原始数据质量限制。结果表明,由原始数据判读的正相时间与采用方法1得到的正相时间相差较大,但是拟合得到的超压峰值相对误差小于4%,正相冲量相对误差小于5%。

表1 不同数据处理方法得到的冲击波参数Table 1 Shock wave parameters by different data processing methods
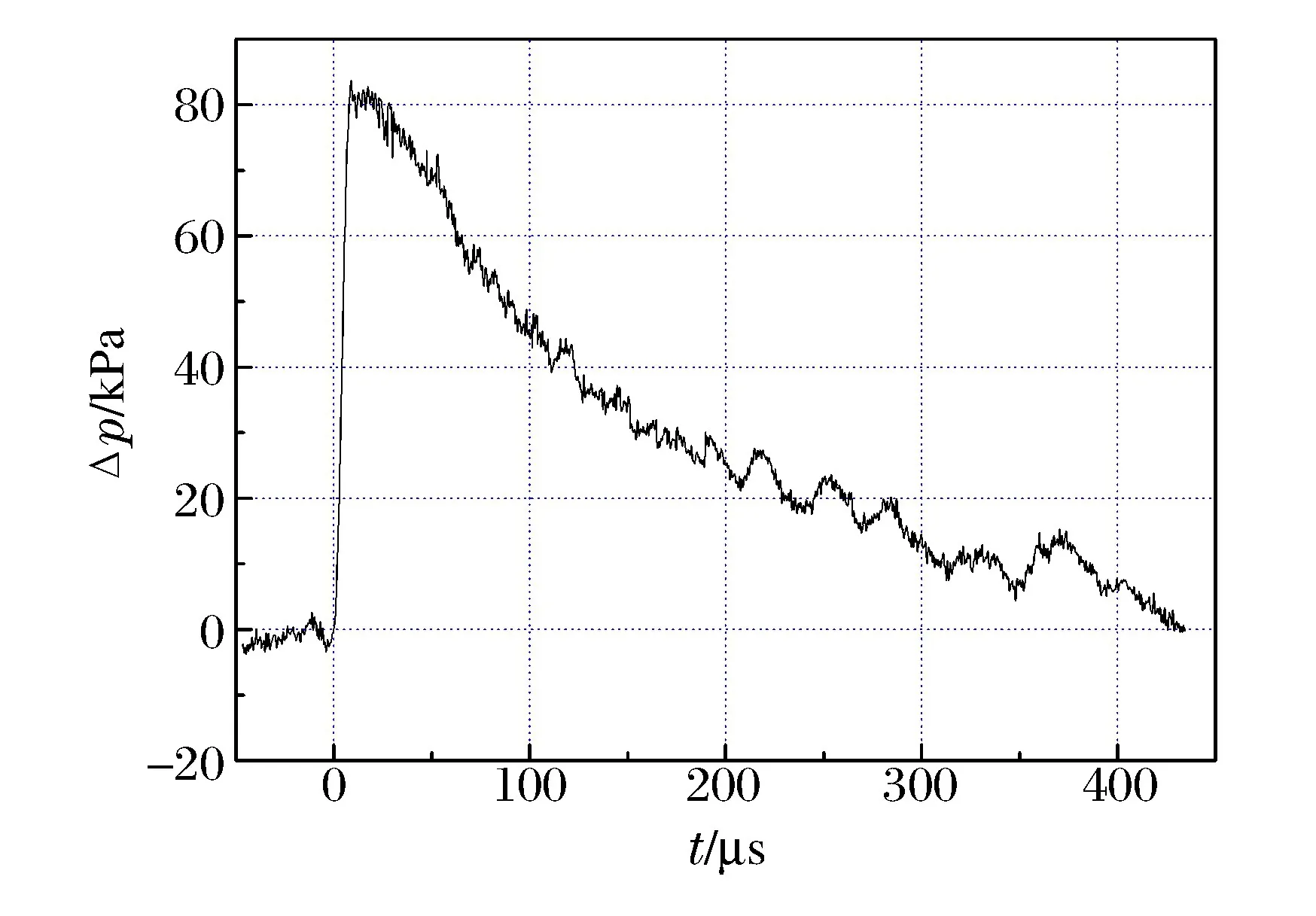
图5 已标定传感器压力时程曲线Fig.5 Overpressure history of standard sensor
3 误差分析
利用公式(1)计算冲击波速度采用了线性近似,并基于假设冲击波到达传感器相同位置时,传感器能够立即响应且有相同的响应时间。但由于传感器敏感材料性能的差异,并不能严格保证以上假设的成立。由于传感器敏感面固有尺寸无法消除,响应位置不同会导致冲击波速度计算的误差,如图6所示,实际冲击波速度为:

式 中:Δs为 传 感 器 相 应 偏 差 距 离,带 来 误 差 ε1=。 传 感 器 敏 感 面 固 有 尺 寸 越 大,则 由 于 响 应 位置不同带来的误差越大,理论最大偏差距离为一个传感器直径长度。
另外,由于每个传感器的响应时间不相同,同样会带来误差。实验采集到的冲击波到达时间点t包含有传感器 的 响 应 时 间td,即 冲 击 波 实 际 到 达 时 间 为t-td,因 此冲击波经过相邻传感器的实际时间为:

图6 不同响应位置误差示意图Fig.6 Scheme of error caused by different response positions

实际冲击波速度为:

本文实验条件较单一,下一步需要进行不同比例距离下的实验验证。尤其是近距离大压力实验会增加冲击波测量参数的不确定度,传感器响应时间等问题对实验结果的影响将会更明显,且冲击波速度的测量精度也需要大大提高,因此其适用性需要进一步验证。
4 总 结
利用传感器序列获得冲击波速度,进而得到的冲击波超压可近似看作理论压力,从而进行传感器的动态标定以及空中爆炸冲击波参数的确定。利用 Modified-Friedlander方程对实验数据进行拟合,比较了原始数据直接读取、固定超压拟合以及固定正相时间拟合3种方法对冲击波参数确定的影响。利用传感器序列计算得到的超压,使固定超压拟合具有一定的物理依据,拟合结果更能反映实际参数。对实验测量和数据处理过程中的误差进行了分析,提出传感器性能、原始数据质量以及拟合方式的选择都会带来相应的误差。
[1]Ethridge N H.A procedure for reading and smoothing pressure-time data from HE and nuclear explosions[R].Army Ballistic Research Laboratories,1965.
[2]Ismail M M,Murray S G.Study of the blast wave parameters from small scale explosions[J].Propellants,Explosives,Pyrotechnics,1993,18(1):11-17.
[3]Kinney G F,Graham K J.Explosive shocks in air[M].2nd Edition.Berlin and New York:Springer-Verlag, 1985:100-104.
[4]张 远 平.池 家 春.压 力 传 感 器 灵 敏 度 的 动 态 标 定 及 超 压 测 量[J].高 能 量 密 度 物 理 ,2007(2):62-64.
[5]张 衍 芳,杜 红 棉,祖 静 .冲 击 波 信 号 后 期 处 理 方 法 研 究[J].工 程 与 试 验,2010,50(4):15-18. Zhang Yan-fang,Du Hong-mian,Zu Jing.Research on post treatment method for shockwave signals[J].Engineering and Test,2010,50(4):15-18.
[6]Biss M M.Characterization of blasts from laboratory-scale composite explosive charges[D].Pennsylvania State U-niversity,2009:124-139.
[7]Rahman S,Timofeev E,Kleine H.Pressure measurements in laboratory-scale blast wave flow fields[J].Review of Scientific Instruments,2007,78(12):125106.
Dynamic calibration of pressure sensors by small-scale explosive experiments in an explosion containment vessel
Xue Bing,Ma Hong-hao,Shen Zhao-wu,Yu Yong
(Department of Modern Mechanics,University of Science and Technology of China, Hefei 230026,Anhui,China)
Air blast experiments of small-scale charges were conducted in an explosion containment vessel.The shock wave velocity was measured by sensor series.And the approximately theoretic peak pressure was determined from the shock wave velocity by using the Rankine-Hugoniot relationship. The sensor was then calibrated,and the relative error of the sensitivity was small.The shock wave parameters were measured and post processed by using the modified-Friedlander equation.The results show that the nonlinear regression by fixing the overpressure is close to the physical fact,and the fitting by fixing the duration has a high precision.Error analysis reveals that the sensor properties and the post-processing methods can produce errors.Experimental results display that the shock wave parameter measuring and post-processing method suggested has a high precision.By this suggested method,the sensor calibration and parameter measurement can be conducted simultaneously.
mechanics of explosion;dynamic calibration;air explosion;pressure sensor;blast vessel; shock wave;sensor series
O384国标学科代码:13035
:A
10.11883/1001-1455(2015)03-0437-05
(责任编辑 张凌云)
2014-03-28;
2014-07-06
国家 自然科学基 金项目(51174183,51134012)
薛 冰(1989— ),男,博士研 究生;通 讯作者:马宏昊,hhma@ustc.edu.cn。

