用浮阻力模型研究 Richtmyer-Meshkov不稳定性诱导混合*

杨 玟,王 丽 丽,2,周 海 兵,2,张 树 道,2

(1.北 京应用物理 与计算数学 研究所,北 京 100094; 2.北京大学应用物理与技术研究中心,北京100871)

用浮阻力模型研究 Richtmyer-Meshkov不稳定性诱导混合*

杨 玟1,王 丽 丽1,2,周 海 兵1,2,张 树 道1,2

(1.北 京应用物理 与计算数学 研究所,北 京 100094; 2.北京大学应用物理与技术研究中心,北京100871)

采用浮阻力模型对激波管低压缩和激光加载高压缩情况下的 Richtmyer-Meshkov不稳定性诱导混合现象进行了研究。通过与实 验 和 理 论 分 析 结 果进 行 比 较 发 现:为 了 达到 好 的 吻 合,Richtmyer-Meshkov不稳 定性情况下 阻力系数的 取值范围(2.0~5.36)比 Rayleigh-Taylor不 稳 定 性 情 况 下 的 值 (3.3~4.0)宽 得多;而在 Richtmyer-Meshkov不稳定性情况下,高压缩时阻力系数的不确定度(约 为3.36)明显高于低压缩 时的值(约为1.46),模型的进一步完善还有待于更精确实验的验证。研究显示:指数律经验公式中指数随工况的不同而显著变化,目前工程设计中采用指数律经验公式是粗糙的。

流体力学;Richtmyer-Meshkov不稳定性;浮阻力模型;扰动界面;压缩比

当冲击作用于不同密度或不同可压缩性2种物质的扰动界面时产生 Richtmyer-Meshkov不稳定性(RMI)。 这 种 不 稳 定 性 理 论 上 由 Richtmyer发 现 并 描 述[1],由 Meshkov 从 实 验 中 证 实[2]。 该 界 面 不稳定性问题在 许多自 然现象 及科学 和工程 领域中 起着重 要作用[3-8],如 超新星 爆炸、磁 化等离 子 体 、磁 约束、太阳磁化层、地下盐矿、火山岛及外壳与内部流体混合导致中子收益降低的激光驱动惯性约束聚变和冲击波与火焰相互作用导致的爆燃转爆轰等。此外,RMI也可能从受冲击的金属表面产生喷射物。

RMI的演化通常经历由不稳定模式的振幅hk和波长λ=2π/k描绘的若干阶段。对于khk≪1,扰动随k Ut呈正比例增长,U 为激波作用后的界面运动速度。当khk达到某一值,非线性使增长率降低,驱动模式耦合,且增长率随着扰动谱宽的增大而减小。然后,由于尖钉下落(重流体进入轻流体)比气泡上升(轻流体进入重流体)快,界面变得不对称。对于宽的不稳定谱,非线性最终导致产生湍流混合层。RMI的脉冲性质令问题复杂,使得 RMI定性上与常见的 Rayleigh-Taylor不稳定性(RTI)不同。由于冲击的可压缩性、复杂的物质特性以及后期的非线性运动直至湍流混合,RMI演化的计算是困难的。当然,随着计算机技术的迅猛发展,这可以采用多维高分辨率流体力学模拟来进行,但它们计算强度大,无法用于工程设计优化研究。因此,目前实际应用中通常采用捕捉较低分辨率时不稳定流动主要特征的 简 化“混 合 模 型 ”[9]。 杨 玟 等[10-11]对 此 进 行 了 尝 试 ,将 传 统 的k-ε模 型 应 用 于 界 面 不 稳 定 性 引 起 的 混合,取得了令人满意的结果。

但是,由于与 RMI相关的其它物理过程非常复杂,较复杂的混合模型(如k-ε)也难以直接应用到工程设计中。目前,很多实际应用中对 RMI诱发混合现象的处理都非常简单,假设混合层宽度以指数形式tθi增长。而大量实验研究表明该比例关系仍不 确 定[3-6],因 为 考 虑 压 缩 性 的 计 算 是 困 难 的,它 们 与 实验不符。即使指数律粗略满足,但不同工况下θi的差别也很大,它显著依赖于初始扰动谱。由此可见,工程设计中对RMI诱发混合现象的处理过于粗糙。

本文中,在简单介绍描述作用于混合层中产生的气泡和尖钉的浮阻力模型基础上,采用该模型对激波管低压缩情况和激光加载高压缩情况下的RMI诱发混合层宽度(气泡与尖钉宽度之和)进行计算,验证模型和选取参数的有效性。

1 模型介绍

目前,典型的 浮阻力 模型可 写为如 下形式[12]:

式 中 :下 角 标i,j表 示 2 种 不 同 的 流 体 ,下 角 标 为 1 时 表 示 重 流 体 (尖 钉 ),为 2 时 表 示 轻 流 体 (气 泡 );ρi为 重 流 体/轻 流 体 的 密 度 ;vi是 尖 钉/气 泡 的 渗 透 速 度 ,且vi=d hi/d t,hi表 示 尖 钉/气 泡 的 瞬 时 宽 度 ;Ca是 附 加 质 量 力 系 数 ;β是 浮 力 产 生 的 模 型 常 数 ;Cd是 阻 力 系 数 ;a(t)为 激 波 脉 冲 加 速 度 ;Vi为 尖 钉/气 泡的体积,Ai为尖钉/气泡的截面积。方程左端第一项为惯性力,第二项为浮力,右端为阻力。关于模型的详细论述可参考文献[13-14],这里不再重复。对于 Richtmyer-Meshkov不稳定性,通常认为冲击简单地给予界面上的气泡和尖钉一个脉冲,则它们随后的运动可以由惯性力和阻力相等来得到(加速度为零)。因此脉冲加速度情况是有启发性的,可以用来研究不稳定性的惯性特性。

本文所求解的模型方程是一组二阶常微分方程,将它们简化为一阶微分方程:d hi/d t=vi;d vi/d t= -fiCdvi|vi|/hi。 采 用 四 阶 Runge-Kutta方 法 进 行 求 解 。

2 结果分析与讨论

采用上述模型和数值方法,对关注的激波管低压缩情况和激光加载高压缩情况下模型的性能进行了考察。这2种工况下RMI产生的机理不同:对于弱冲击,主要贡献来自于压力梯度和密度梯度不重合引起的旋涡沉积;对于强冲击,存在激波在经折射后产生了显著的反射,这产生增长率的振荡,但它们最终衰减。

2.1 激波管低压缩的情况下的模拟

首先采用上述模型对4种不同激波脉冲加速度情况下气泡和尖钉宽度进行了计算。图1给出了所采用的4种加速度曲线,g为重力加速度。脉冲加速 度a约 为150g,持 续 时 间t0约 为10 ms。 这 些 曲线 为 LANL 的 Dimonte 等 LEM(Linear Electric Motor)实 验 的 测 量 曲 线[15]。 实 验 中 流 体 和 脉 冲 加速 度 的 性 质 参 数 见 表1,其 中R为 密 度 比,R=(1+ A)(1-A),A为 Atwood 数, We为韦伯数,Re为雷诺数。对于每一种情况,通过调整 阻 力 系 数Cd和 初 始 振 幅hi0来 使 随 时 间 变 化 的解与实验数据相符。但是,数值实验发现:在大多数情 况 下hi0对 结 果 的 影 响 远 小 于Cd的 影 响 。

图2给出了4种加速度驱动下气泡和尖钉宽度随 位 移Z的 变 化,,激 波 作 用 时Z≈Ut。

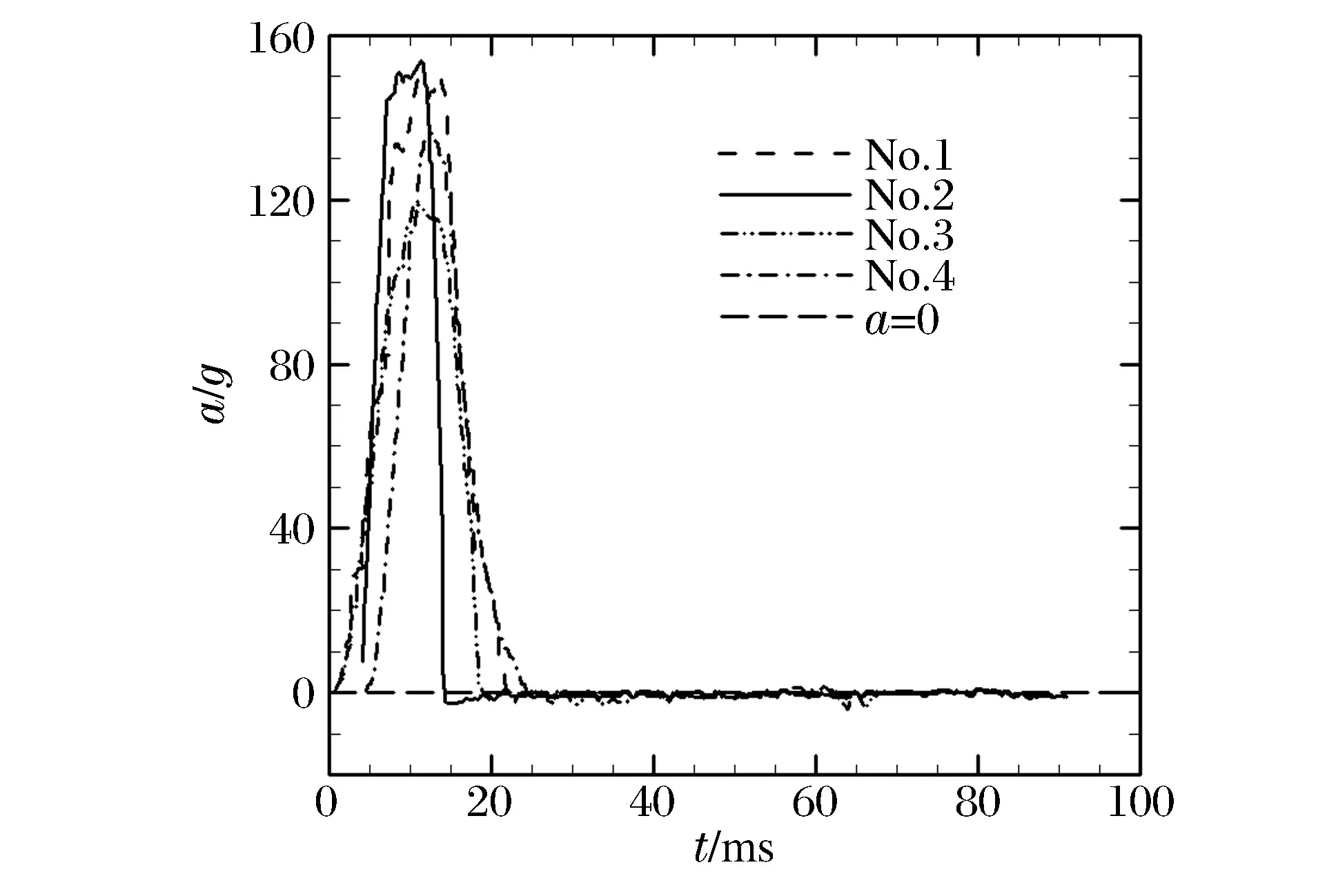
图1 计算采用的4种不同脉冲加速度曲线Fig.1 Four kinds of impulsive accelerations used in the calculation

由图可见,4种加速度情况下计算的气泡和尖钉宽度与实验基本吻合。计算中阻力系数Cd的取值为3.67±0.73,与文献[16]中分析得到的Cd的不确定度1.2接近。从图中还可看 出:气泡和尖钉的 不 对称性随着密度 比R的增大 而增大 。此外 ,本文 中还对 实验结 果按指 数 律hi=hi0tθi进 行 了 拟 合,其 中hi0的 取 值 范 围 为 0.5~1.0 cm。R=49.1 时 ,θ1≈0.85,θ2≈0.33;R=23.4 时 ,指 数 迅 速 下 降 ,θ1≈0.45,θ2≈0.24;R=1.57 时 ,θ1≈0.28,θ2≈0.22。 由 此 可 见 ,指 数θi随 密 度 比 变 化 而 变 化 ,但 具 体 变 化 规 律还未从数值模拟和实验中最终确定,这主要是由于θi对实验初始条件敏感,需要计算和实验之间更直接的比较。

表1 实验中采用的流体和脉冲加速度性质参数Table 1 Fluid combinations and characteristics for impusive accerleration experiments

图2 气泡和尖钉宽度随位移的变化Fig.2 The width of bubble and spike with displacement

2.2 激光加载高压缩情况下的模拟

为了考察模型在高压缩情况下的性能,我们进一步对 Nova激光器上马赫数 Ma>10的实验进行了模 拟。 实 验 采 用 一 靶 丸 装 置 在 Nova 激 光 器 上 进 行[17]。 流 体 1 由 厚 度 为 125μm、初 始 密 度 为1.7 g/cm3的铍烧蚀层组成。流体2是未压缩密度为0.12 g/cm3的泡沫。波速为46 km/s的入射冲击与界面相互作用产生反射稀疏波和速度为3 km/s的透射激波。界面经加速后速度为56 km/s,物质被压 缩 后 ,ρ1=2 g/cm3,ρ2=0.5 g/cm3,A=-0.6。 这 些 参 数 通 过 对 比 热 比γ1=1.8 和γ2=1.45 的 流 体求解理想的黎曼问题得到。

图3给出了 Nova实验中计算的加速度曲线。由图可见,激光驱动在4 ns后停止,这导致泡沫减压,由于A<0而产生 Rayleigh-Taylor(RT)分量,因此冲击压缩后流动是亚音速的,本文模型是适用的。图4给出了混合区总宽度H随位移Z的变化(由于实验不能分辨气泡和尖钉,因此给出了总振幅H)。从图中可看出:混合区总宽度的计算值与实验值吻合,而且Cd=2.0和Cd=5.36的曲线之间包括了全部的实验数据。但是,阻力系数Cd的不 确 定 度约为 3.36,明 显 大 于低压缩情况 的 值(约 为1.46)。此外,拟合得到总的混合宽度以指数为0.5的指数律增长,这超过了激波管低压缩时得到的指数,推测其原因可能是:(1)激光驱动随时间减小,使得压力降低、界面减速,这导致扰动膨胀,并引入 RT 分量(因为Aa>0)。这些影响可能显著增加推测的指数;(2)A=0.6时 Nova上的初始扰动比激波管 上 的更对称,如果指数对初始条件敏感,这可能导致不同的指数。

图3 Nova实验中的加速度曲线Fig.3 Acceleration history for Nova experiment

图4 混合区宽度随位移的变化Fig.4 Variaion of total width with displacement

3 结 论

采用浮阻力模型对激波管低压缩和激光加载高压缩情况下 Richtmyer-Meshkov不稳定性诱发的物质渗透边界的演化过程进行了计算,计算结果与实验吻合得较好。这表明本研究中模型参数的选取、方程中现象学比例因子的添加和模型假设是合适的。但是由于实验测量的局限性,模型中的一些问题仍然是突出的,包括阻力项的大小和形式、压缩的影响、“附加质量”的描述等。为了更好地评估模型,需要一些实验上的完善。首先,气泡和尖钉必须单独分辨,因为它们的表现相当不同,尤其在A较大的情况。其次,实验持续时间应当延长至足以揭示模型的差别为止。尽管如此,本文模型仍明显优于当前实际应用中所采用的经验公式(本研究也显示指数θi随工况的不同而显著变化)。

[1]Richtmyer R D.Taylor instability in shock acceleration of compressible fluids[J].Communicational Pure Applied Mathematics,1960,13(1):297-319.

[2]Meshkov E E.Instability of the interface of two gases accelerated by a shock wave[J].Soviet Fluid Dynamics, 1969,4(1):101-104.

[3]Dimonte G,Remington B.Richtmyer-Meshkov experiments on the Nova laser at high compression[J].Physical Review Letters,1993,70(12):1806-1809.

[4]Dimonte G,Frerking C E,Schneider M.Richtmyer-Meshkov instability in the turbulent regime[J].Physical Review Letters,1995,74(24):4855-4858.

[5]Vetter M,Sturtevant B.Experiments on the Richtmyer-Meshkov instability of an air/SF6interface[J].Shock Waves,1995,4(5):247-252.

[6]Jourdan G,Houas L,Haas J F,et al.Thickness and volume measurements of a Richtmyer-Meshkov instability induced mixing zone in a square shock tube[J].Journal of Fluid Mechanics,1997,349:67-94.

[7]Alon U,Hecht J,Ofer D,et al.Power laws and similarity of Rayleigh-Taylor and Richtmyer-Meshkov mixing fronts at all density ratios[J].Physical Review Letters,1995,74(4):534-537.

[8]Aglitskiy Y,Velikovich A L,Karasik M,et al.Basic hydrodynamics of Richtmyer-Meshkov-type growth and os-cillations in the inertial confinement fusion-relevant conditions[J].Philosophical Transactions of Royal Society A, 2010,368(1916):1739-1768.

[9]Llor A.Statistical hydrodynamic models for developed mixing instability flows[S].Springer,2005.

[10]杨 玟,王 丽丽 ,张树 道.Rayleigh-Taylor不稳定性诱 导湍流混合 的数值模拟[J].工程力 学,2011,28(6):236-241. Yang Min,Wang Li-li,Zhang Shu-dao.Numerical simulation of turbulent mixing induced by Rayleigh-Taylor instability[J].Engineering Mechanics,2011,28(6):236-241.

[11]杨玟,王丽丽,张树道,等.用湍流模型 研 究 Richtmyer-Meshkov不稳定性 诱 导的湍流 混 合[J].空气动 力 学学报, 2010,28(1):119-123. Yang Min,Wang Li-li,Zhang Shu-dao,et al.The study of turbulent mixing induced by Richtmyer-Meshkov instability using turbulence model[J].Acta Aerodynamica Sinica,2010,28(1):119-123.

[12]Cheng B.Modeling chaotic mixing[J].Nuclear Weapons Journal,2010,1:8-17.

[13]Layzer D.On the gravitational instability of two superposed fluids in a gravitational field[J].Astrophysics Journal,1955,122(1):1-12.

[14]杨玟,王丽 丽,周 海兵 ,张树 道.用浮阻 力模型研究 Rayleigh-Taylor不稳定性诱 发混合现象[J].工程力 学,2013,30 (4):385-391. Yang Min,Wang Li-li,Zhang Shu-dao.Study on mixing induced by Rayleigh-Taylor instability using buoyancydrag model[J].Engineering Mechanics,2013,30(4):385-391.

[15]Dimonte G,Schneider M.Density ratio dependence of Rayleigh-Taylor mixing for sustained and impulsive acceleration histories[J].Physics of Fluids,2000,12(2):304-321.

[16]Dimonte G,Schneider M.Turbulent Richtmyer-Meshkov instability experiments with strong radiatively driven shocks[J].Physics of Plasmas,1997,4(12):4347-4357.

[17]Dimonte G.Nonlinear evolution of the Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J].Physics of Plasmas,1999,6(5):2009-2015.

Study on mixing induced by Richtmyer-Meshkov instability by using buoyancy-drag model

Yang Min1,Wang Li-li1,2,Zhou Hai-bing1,2,Zhang Shu-dao1,2
(1.Insitute of Applied Physics and Computational Mathematics,Beijing 100094,China; 2.Center for Applid Physics and Tchnology,Peking University,Beijing 100871,China)

The mixing induced by Richtmyer-Meshkov instability under lower and high compression ratios is studied by using buoyancy-drag model.It is found by the comparison between the experimental and theoretical analytic results that in order to achieve good agreement,the range of the drag coefficient value chosen in Richtmyer-Meshkov instability is much wider than that in Rayleigh-Taylor instability;while in Richtmyer-Meshkov instability the uncertainty of the drag coefficient under high compression is larger than that under lower compression.It is pointed that the further improvement of the model needs to be validated by more accurate experiment.Moreover the study reveals that the exponent in empirical expression varies with calculation conditions remarkably and the use of the empirical expression in current engineering design is rough.

fluid mechanics;Richtmyer-Meshkov instability;buoyancy-drag model;disturbed interface;compression ratio

O358国标学科代码:13025

:A

10.11883/1001-1455(2015)03-0423-05

(责任编辑 王小飞)

2013-11-28;

2014-06-28

国家 自然科学基 金项目(11072040);装 备预研重点 实验室基金 项目(9140C690204120C69259);中国 工程物理研 究院科学技 术发展基金 项目(2012B0201028、2012B0201030)

杨 玟(1970- ),女,博士,副研究员,yang_min@iapcm.ac.cn。