一种改进的鸡群算法

孔飞，吴定会

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122)

一种改进的鸡群算法

孔飞，吴定会*

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122)

针对鸡群算法在求解高维优化问题时易陷入局部最优和出现早熟收敛的情况，提出一种改进的鸡群算法。算法中对小鸡的位置更新公式中加入向小鸡自身所在群中的公鸡学习部分，并引入惯性权值和学习因子，然后用改进的鸡群算法对8个基本测试函数进行求解。仿真实验时与粒子群算法、蝙蝠算法和鸡群算法进行对比。结果表明，该算法在求解优化问题时易于跳出局部最优，避免早熟收敛，尤其对于高维问题，该算法相比其他进化算法，更容易找到全局最优值。

群体智能;等级秩序;鸡群算法;测试函数;复杂度分析

群体智能优化算法(Swarm Intelligence Algorithm，SIA)是通过模拟自然界生物的群体行为而构造的随机优化算法［1］，如粒子群算法［2］(Particle Swarm Optimization，PSO)、蚁群算法［3］(Ant Colony Optimization，ACO)、人工蜂群算法［4］(Artificial Bee Colony，ABC)、人工鱼群算法［5］(Artificial Fish Swarm Algorithm，AFSA)、蝙蝠算法［6］(Bat Algorithm，BA)等。这些算法为解决大量存在于计算科学、工程科学、管理科学等领域的全局优化问题提供了新的求解途径，因此成为科研人员长期研究的热点。全浩军等［7］将改进的人工鱼群算法用于软硬件划分;王泽兵等［8］将粒子群算法用于动态热释电目标跟踪;罗慧等［9］将动态蚁群算法用于模拟电路最优测点选择。新的智能算法仍在不断出现，如磷虾群优化算法［10］、混沌果蝇算法［11］、蜘蛛算法［12］等。所有的这些算法都是从自然界中各种生物种群生活规律中抽象出来的。

鸡群算法(Chicken Swarm Optimization，CSO)是由MENG Xianbing等［13］于2014年提出的一种基于鸡群搜索行为的随机优化方法，它模拟了鸡群等级制度和鸡群行为。整个鸡群分为若干子群，每一个子群都由一个公鸡、若干母鸡和小鸡组成。不同的鸡遵循不同的移动规律，在具体的等级制度下，不同的鸡群之间存在竞争，它是一种全局优化算法。相比粒子群算法、蝙蝠算法和差分进行算法［14］，该算法具有收敛速度快和收敛精度高的优点。但是文献［13］只是对标准测试函数在低维情况下加以求解，并没有对高维问题进行求解和相关的分析。文中分析了文献［13］提出的算法在对高维优化问题求解时，收敛精度变低，算法容易陷入局部最优，出现早熟收敛情况。文中提出了一种改进的鸡群算法(Improved Chicken Swarm Optimization，ICSO)，算法中对小鸡的位置更新公式中加入向小鸡自身所在群中的公鸡学习部分，并引入惯性权值和学习因子，在保证算法收敛速度的同时尽可能提高算法的收敛精度，防止算法出现早熟收敛情况。通过对基本测试函数的求解验证了所提算法的可行性和先进性。

1 鸡群优化算法

在描述算法前，先进行如下假设:

1)整个鸡群中存在着若干子群，每个子群都由一个公鸡、若干母鸡和一些小鸡组成。

2)如何把鸡群分成若干子群以及如何确定鸡的种类取决于鸡自身的适应度值。鸡群中，适应度值最好的若干个体作为公鸡，并且每只公鸡都是一个子群的头目;具有最差适应度值的若干个体作为小鸡;剩余的个体就作为母鸡。母鸡随便选择属于哪个子群，母鸡和小鸡的母子关系也是随机建立的。

3)鸡群中的等级制度、支配关系和母子关系一旦建立就保持不变，直至数代以后才开始更新。

4)每个子群中的个体都围绕这个子群中的公鸡寻找食物，也可以阻止其他个体抢夺自己的食物;并且假设小鸡可以随机偷食其他个体已经发现的食物，每只小鸡跟随它们的母亲一起寻找食物。鸡群中具有支配地位的个体具有良好的竞争优势，它们先于其他个体找到食物。

在解决优化问题时，鸡群中的每个个体都对应优化问题的一个解。假设NR，NH，NC和NM分别为公鸡、母鸡、小鸡和妈妈母鸡的个数。在整个鸡群中，所有的个体数假设为N，每个个体的位置xij(t)表示第i个体的j维在第t次迭代的值。

整个鸡群有3种类型的鸡，鸡群中个体位置更新公式随着鸡种类的不同而不同。公鸡对应鸡群中适应度值最好的个体，它们可以在更广泛的空间寻找食物，公鸡对应的位置更新公式如下:

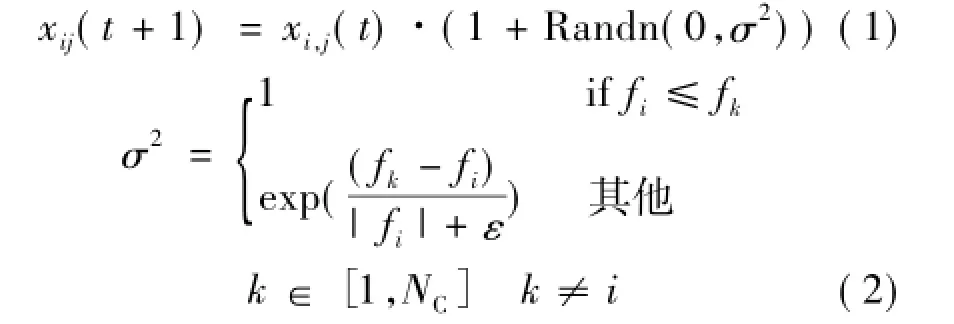
式中:Randn(0，σ2)为均值为0，标准差为σ2的一个高斯分布;ε为一个很小的常数;k为所有公鸡中除去i后的任一个体。

母鸡的位置更新公式如下:

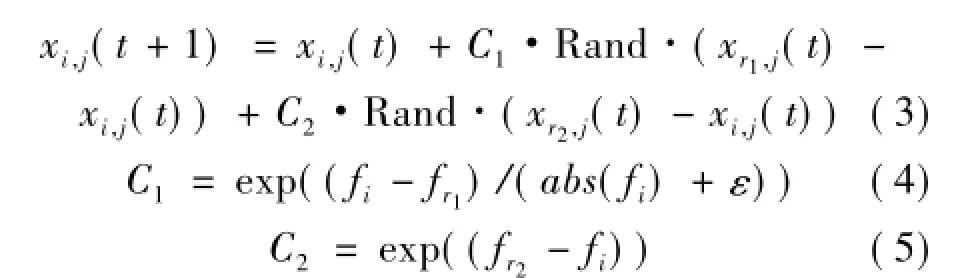
式中:Rand为［0，1］之间均匀分布的随机数;r1为第i只母鸡自身所在群中的公鸡;r2为整个鸡群中公鸡和母鸡中随机选取的任意个体，且r1≠r2。小鸡的位置更新公式如下:

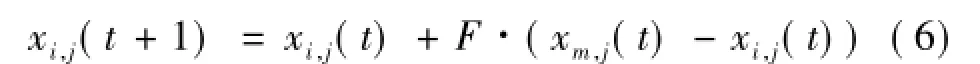
式中:m为第i只小鸡对应的母鸡;F(F∈［0，2］)为跟随系数，表示小鸡跟随母鸡寻找食物。

2 改进的鸡群算法

2.1 鸡群算法分析

文中采用文献［13］中算法对4个标准测试函数在高维条件下进行了求解，并对比了其他两种算法，求解结果见表1。

由表1可以看出，当D=100时，鸡群算法的求解结果虽然好于粒子群算法和蝙蝠算法的求解结果，但是已明显偏离了全局最优值，尤其是对于Rosenbrock函数算法明显陷入局部最优，出现早熟收敛现象。

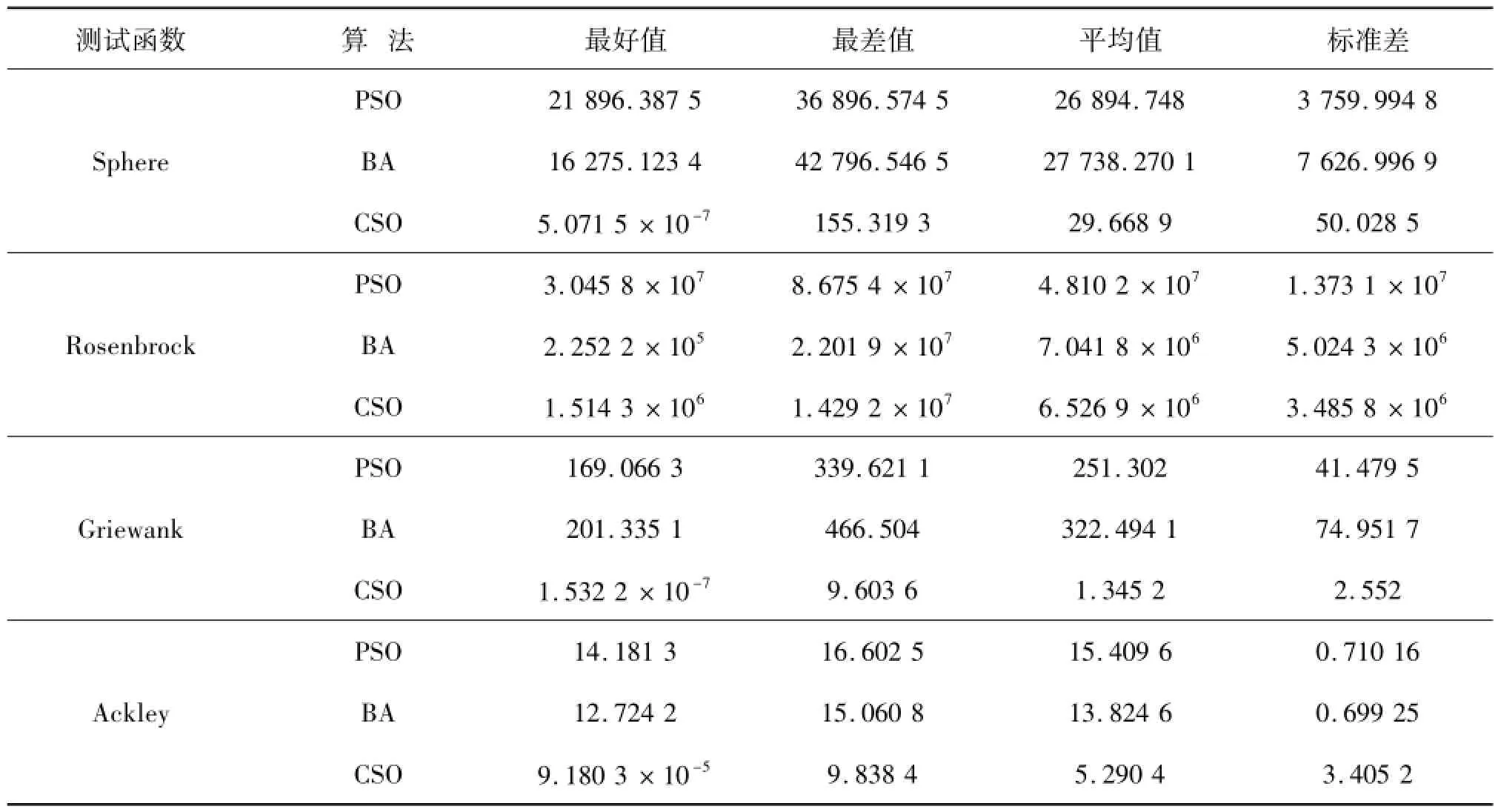
表1 CSO和其他算法对于4个标准测试函数在D=100求解结果比较Tab.1 Com parison betw een the results of CSO and other algorithm s for D=100

2.2 改进的鸡群算法

对于式(6)中的小鸡位置更新公式，小鸡只向自己的妈妈学习，而并没有向小鸡自身所在群中的公鸡学习。小鸡在更新自己的位置时只能获取自己妈妈的位置信息，而无法获取整个子群中公鸡的位置信息。当妈妈母鸡陷入局部最优时，小鸡因为只向自己的妈妈学习，也会陷入局部最优。因此，鸡群算法会陷入局部最优。文中对小鸡的位置更新公式进行了改进，更新公式中加入了向小鸡自身所在群中的公鸡学习部分。改进后的位置更新公式如下:式中:m为小鸡对应的妈妈母鸡;r为妈妈母鸡自身所在群中的公鸡;C为学习因子，表示小鸡向自身所在群中公鸡学习的程度;w为小鸡的自我学习系数，这与粒子群算法中的惯性权重很相似。

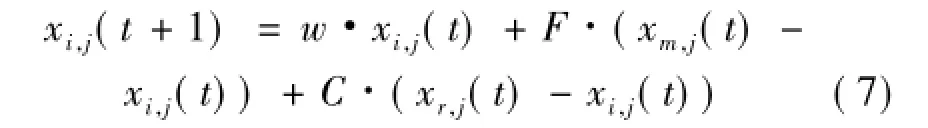
算法的详细流程如下:

1)初始化鸡群x，并定义相关参数NR，NH，NC，NM等;

2)计算鸡群的适应度值fitness，初始化个体当前最好位置Pbest和鸡群全局最好位置gbest，t=1;

3)如果t%G=1，排序fitness，建立鸡群的等级制度，将鸡群分成数个子群并确定母鸡和小鸡的对应关系;

4)使用式(1)、式(3)和式(7)分别更新公鸡、母鸡和小鸡的位置并分别计算每个个体的适应度值;

5)更新鸡群的个体当前最好位置和鸡群全局最好位置;

6)t=t+1，如果满足迭代停止条件，则停止迭代，输出最优值，否则转到3)。

2.3 参数分析

G的取值对文中算法的收敛精度和收敛速度能产生重要影响。G取值太大，算法不能快速收敛到全局最优值，影响算法的收敛速度;G取值太小，算法容易陷入局部最优值。文中通过对测试函数的测试，得出以下结论:当G=10时，算法在保证收敛精度的同时，收敛速度明显提高。此外，在综合考虑算法的收敛精度、收敛速度和鲁棒性的情况下，F取［0.4，1］之间的随机数，C=0.4，w随迭代次数的增加从0.9到0.4指数递减。w的计算公式

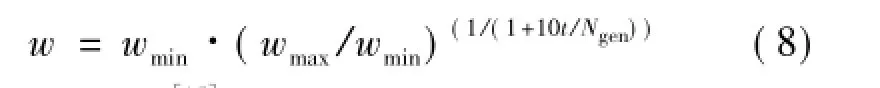
如公式(7)所示［15］。

3 仿真实验分析

3.1 参数设置

使用表2列出的8个基本测试函数对文中算法的有效性进行验证［16-17］，仿真中对比了标准PSO，CSO和BA算法。为了得到客观评价，4种算法对每一个测试函数独立运行30次，种群规模都为100，每次运行的最大迭代次数均为1 000，分别在D=10和D=100的情况下对所有的测试函数进行求解。4种算法其他相关参数见表3。

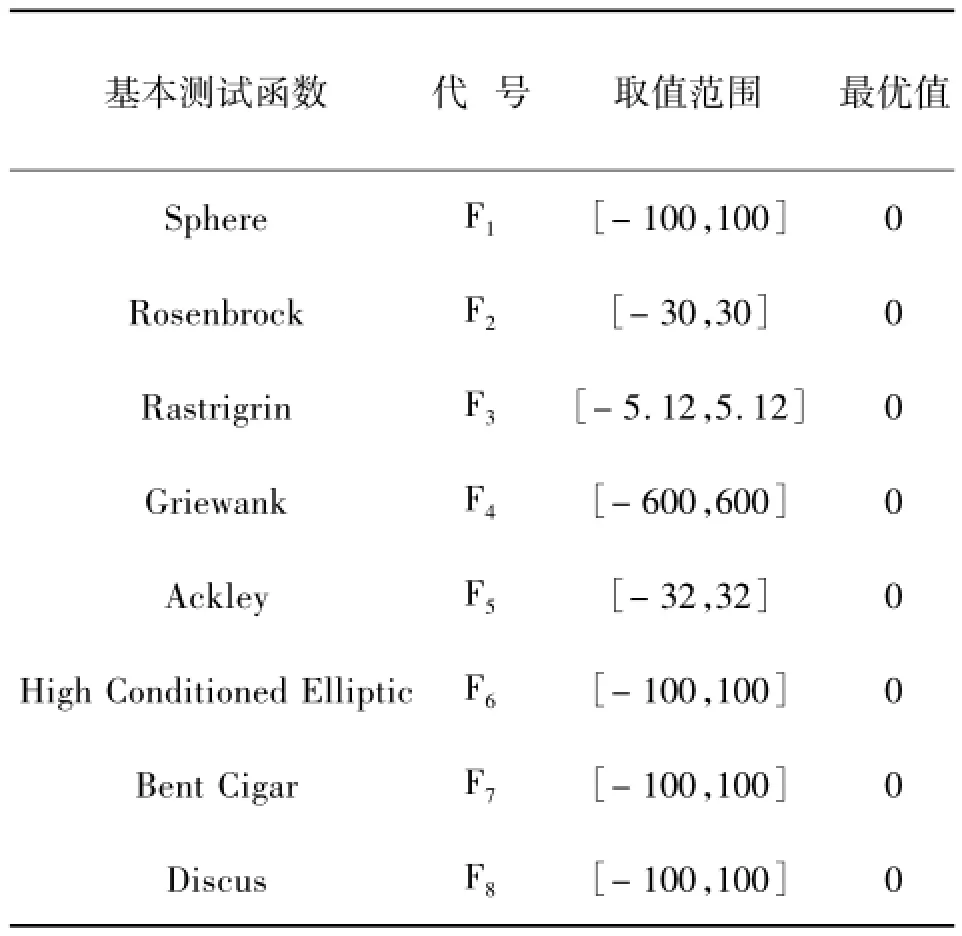
表2 8个标准测试函数Tab.2 Eight benchm ark prob lem s

表3 算法的相关参数设置Tab.3 Related parameter values

3.2 仿真分析

4种算法对每一个测试函数独立运行30次，求出30次运行结果的最好值、最差值、平均值和标准差，结果列于表4、表5中。

表4 文中算法和其他算法对标准测试函数在D=10的求解结果比较Tab.4 Com parison between the resu lts of ICSO and other algorithms for D=10

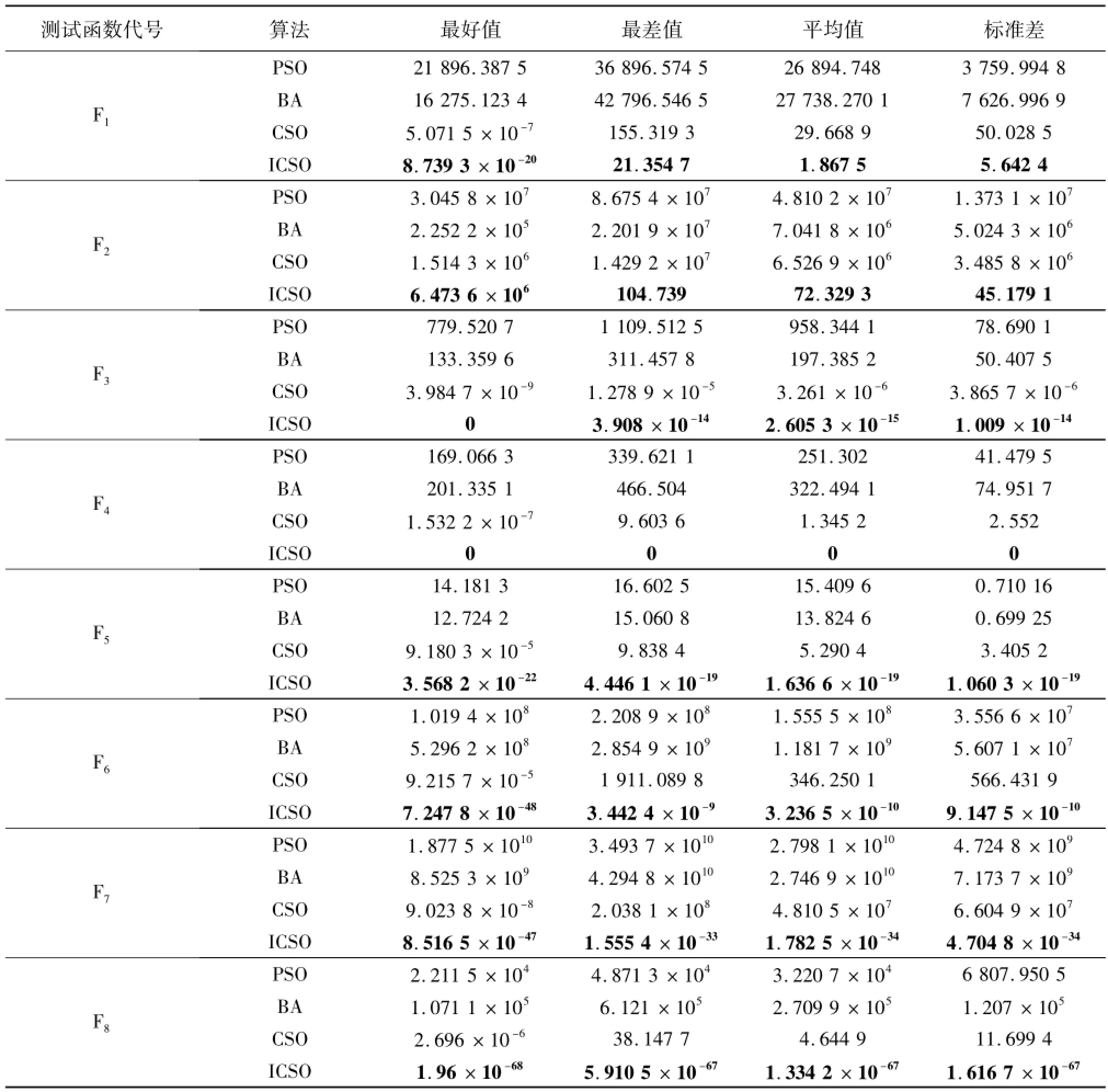
表5 文中算法和其他算法对标准测试函数在D=100的求解结果比较Tab.5 Com parison betw een the results of ICSO and other algorithm s for D=100

由表4可以看出，在D=10时，对于大部分测试函数而言，ICSO的求解结果要好于CSO的求解结果，且ICSO和CSO的求解结果要远远好于PSO和BA的求解结果。

由表5可以看出，在D=100时，对于这8个测试函数而言，ICSO的求解结果均好于CSO的求解结果，且远远好于PSO和BA的求解结果;尤其对于测试函数F2，F5，F6，F7和F8而言，ICSO的求解结果要远远好于CSO的求解结果。

4种算法分别对于测试函数代号F1～F8(以下简称Fx函数)，在D=100时，独立运行30次，获得的平均值收敛曲线如图1～图8所示。

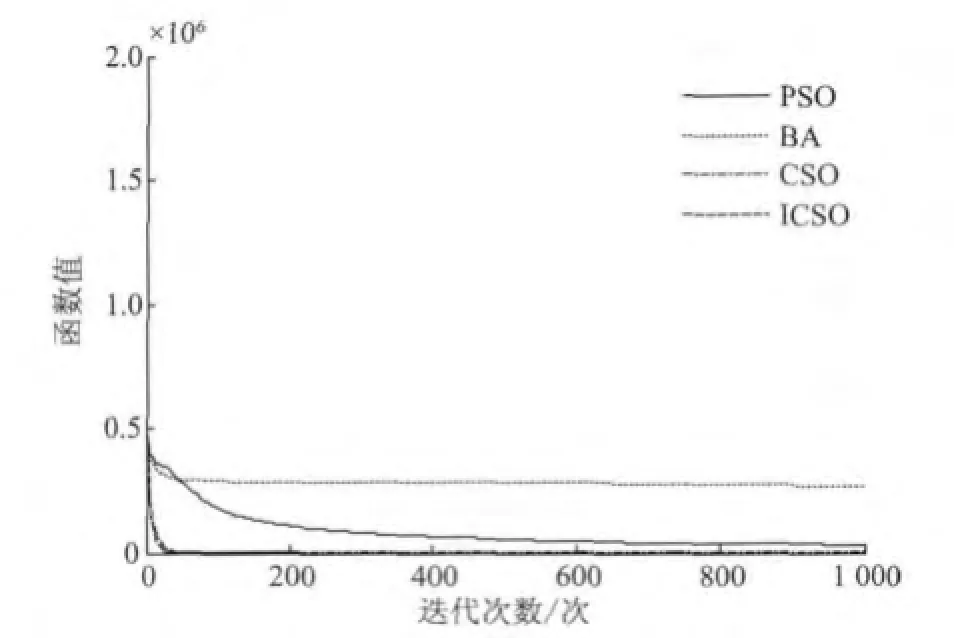
图1 4种算法在D=100对F1函数平均收敛曲线Fig.1 Average convergence curves for F1at D=100

图2 4种算法在D=100对F2函数平均收敛曲线Fig.2 Average convergence curves for F2at D=100

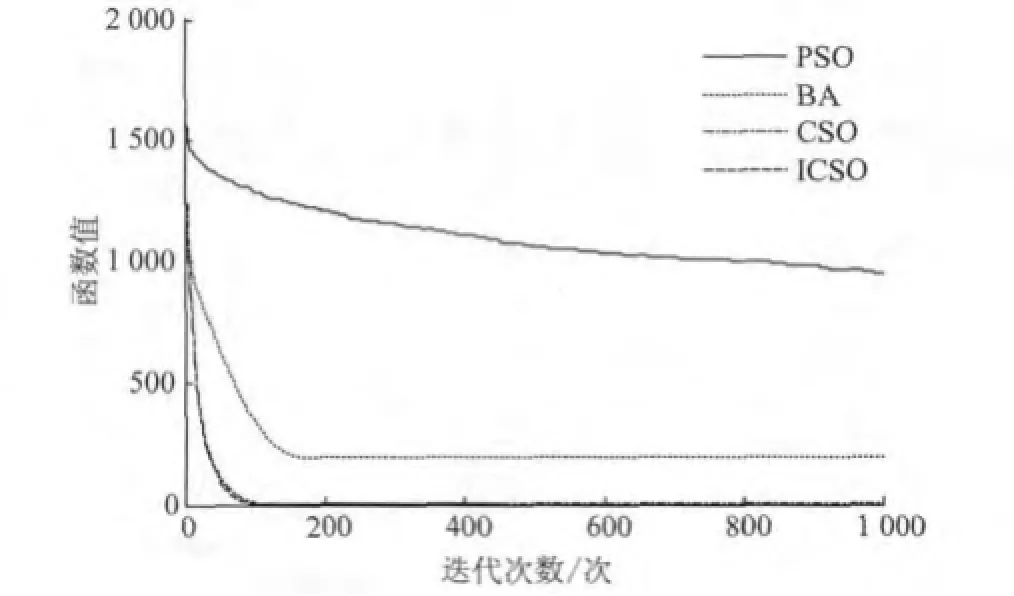
图3 4种算法在D=100对F3函数平均收敛曲线Fig.3 Average convergence cu rves for F3at D=100

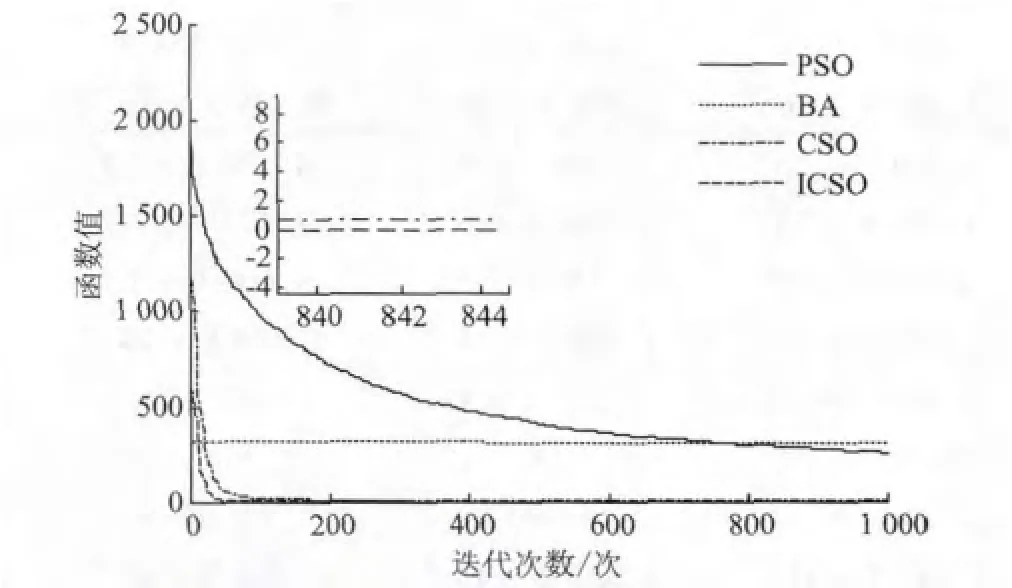
图4 4种算法在D=100对F4函数平均收敛曲线Fig.4 Average convergence cu rves for F4at D=100

图5 4种算法在D=100对F5函数平均收敛曲线Fig.5 Average convergence curves for F5at D=100

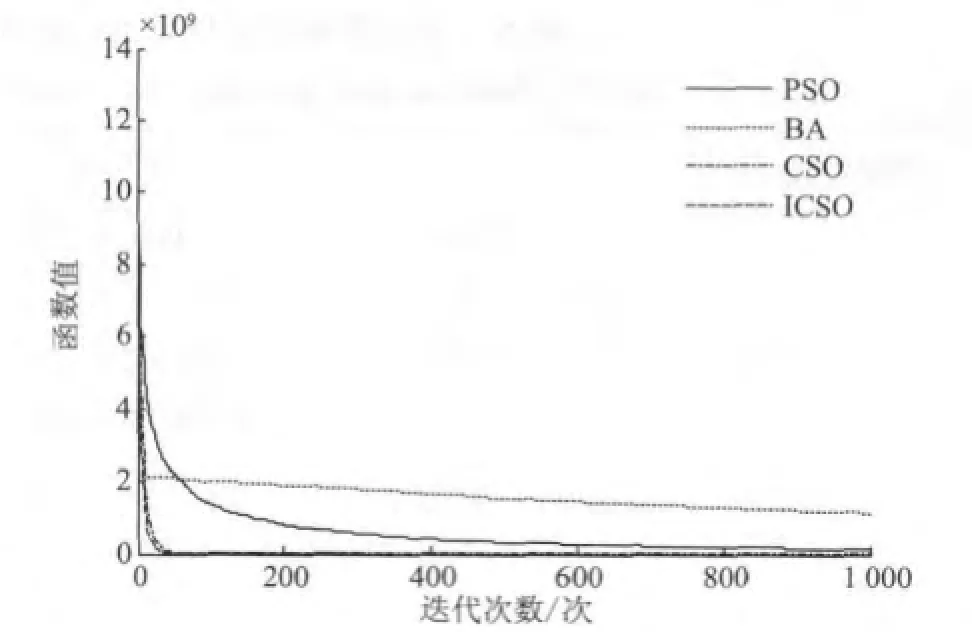
图6 4种算法在D=100对F6函数平均收敛曲线Fig.6 Average convergence curves for F6at D=100

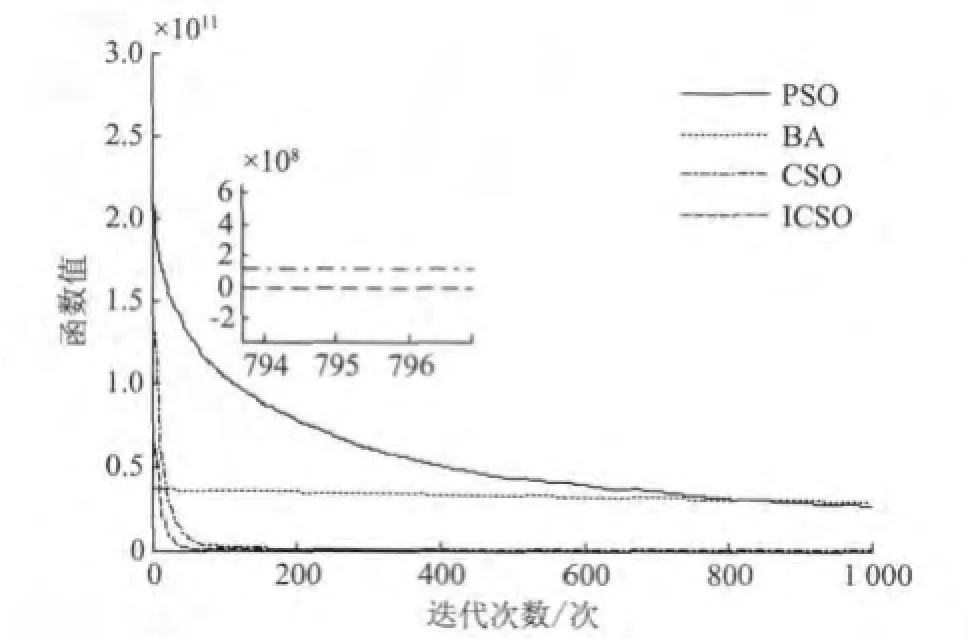
图7 4种算法在D=100对F7函数平均收敛曲线Fig.7 Average convergence curves for F7at D=100

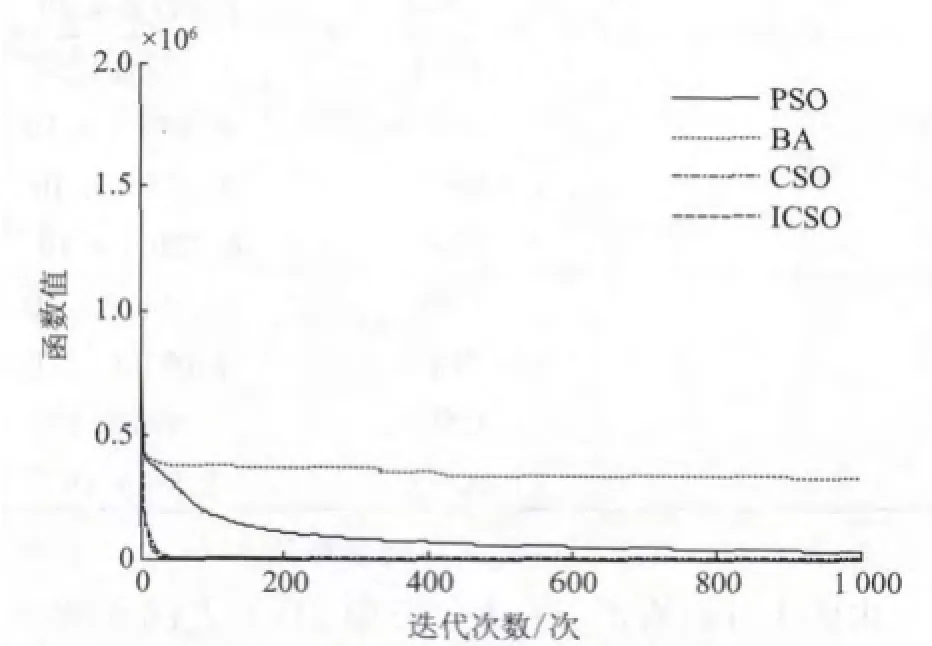
图8 4种算法在D=100对F8函数平均收敛曲线Fig.8 Average convergence curves for F8at D=100

由图1～图8可以看出，在D=100时，就F1～F8函数而言，ICSO的收敛精度均高于CSO算法，且远远高于PSO和BA。在收敛速度方面，对于F2，F4，F5，F6，F7和F8函数而言，ICSO要优于CSO，PSO和BA;对于F1和F3函数而言，ICSO和CSO收敛速度相当，且优于PSO和BA。

3.3 算法复杂度分析

算法的复杂度评价主要包括两个方面:时间复杂度评价和空间复杂度评价。时间复杂度指算法迭代一次所需要最多步骤的时间复杂度之和，通常用数量级符号阶次o表示，如常数阶o(1)。空间复杂度指算法在计算机内执行时所需最大存储空间的度量。由于ICSO与其他3种算法的空间复杂度相当，所有这里只讨论一下算法的时间复杂度。

对于群体智能优化算法而言，算法的时间复杂度正比于问题的优化规模D和群体中个体的数目N。由于ICSO与CSO的时间复杂度相同，这里只列出了3种算法在一次迭代中所需要的主要步骤以及对应的时间复杂度，统计结果见表6。

表6 3种算法的时间复杂度分析Tab.6 Time com plexity analysis of three algorithm s

由表6中可以看出，PSO，BA和ICSO的算法运行时间分别为2N+4ND，2N+6ND和N+4ND。可以看出这3种算法的时间复杂度是相同的，但是ICSO比PSO和BA算法语句执行次数少，因而消耗的时间少。

4 结语

为了克服鸡群算法在求解高维问题时发生早熟收敛，文中提出一种改进的鸡群算法，算法在小鸡的位置更新公式中加入向小鸡自身所在群中的公鸡学习部分，并引入学习因子和惯性权重。对于8个基本测试函数的仿真结果表明，文中算法在求解优化问题时易于跳出局部最优，避免了早熟收敛问题，尤其对于高维问题而言，文中算法相比其他进化算法，更容易找到全局最优值。此外，在算法的执行时间上，文中算法明显少于粒子群算法和蝙蝠算法。所以文中提出的算法具有可行性和先进性。

［1］Beheshti Z，Shamsudding SM H.A review of population-based meta-heuristic algorithms［J］.Int JAdv Soft Comput Appl，2013，5(1):1-35.

［2］Kennedy J，Eberhart R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth Australsa:IEEE Press，1995:1942-1948.

［3］Dorigo M，Maniezzo V，Colorni A.Ant system:optimization by a colony of cooperating agents［J］.IEEE Transactions on Systems Man and Cybernetics，Part B:Cybernetics，1996，26(1):29-41.

［4］Karaboga D.An idea based on honey bee swarm for numerical optimization［R］.Kayseri:Erciyes University，2005.

［5］LI X L，SHAO Z J，QIAN J X.An optimizing method based on autonomous animats:fish-swarm algorithm［J］.Systems Engineering Theory and Practice，2002，22(11):32-38.

［6］YANG X S.A new metaheuristic bat-inspired algorithm［C］//Nature Inspired Cooperative Strategies for Optimization(NICSO 2010).Berlin Heidelberg:Springer，2010.

［7］全浩军，张涛，郭继昌.基于改进人工鱼群算法的软硬件划分方法［J］.天津大学学报:自然科学与工程技术版，2013，46 (10):923-928.

QUAN Haojun，ZHANG Tao，GUO Jichang.Hardware/software partitioning method based on improved artificial fish swarm algorithm［J］.Journal of Tianjin University:Science and Technology，2013，46(10):923-928.(in Chinese)

［8］王泽兵，杨卫，秦丽.基于粒子群算法的动态热释电目标跟踪［J］.光学学报，2014，34(10):35-41.

WANG Zebing，YANG Wei，QIN Li.Target tracking based on particle swarm optim ization using dynamic pyroelectric infrared sensor［J］.Acta Optica Sinica，2014，34(10):35-41.(in Chinese)

［9］罗慧，蹇兴亮，卢伟.基于动态蚁群算法的模拟电路最优测点选择［J］.仪器仪表学报，2014，35(10):2231-2237.

LUO Hui，JIAN Xingliang，LUWei.Optimal test node selection based on dynamic ant colony algorithm for analog circuit［J］.Chinese Journal of Scientific Instrument，2014，35(10):2231-2237.(in Chinese)

［10］Gandomi A H，Alavi A H.Krill herd:a new bio-inspired optim ization algorithm［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17(12):4831-4845.

［11］LEIX，DU M，XU J，et al.Chaotic fruit fly optimization algorithm［C］//5th International Conference on Swarm Intelligence.Hefei:Springer International Publishing，2014:74-85.

［12］Cuevas E，Cienfuegos M，Zaldívar D，et al.A swarm optimization algorithm inspired in the behavior of the social-spider［J］.Expert Systems with Applications，2013，40(16):6374-6384.

［13］MENG X B，LIU Y，GAO X Z，et al.A new bio-inspired algorithm:chicken swarm optimization［C］//5th International Conference on Swarm Intelligence.Hefei:Springer International Publishing，2014:86-94.

［14］Das S，Suganthan PN.Differential evolution:a survey of the state-of-the-art［J］.IEEE Transactions on Evolutionary Computation，2011，15(1):4-31.

［15］陈贵敏，贾建援，韩琪.粒子群优化算法的惯性权值递减策略研究［J］.西安交通大学学报，2006，40(1):53-56，61.

CHEN Guimin，JIA Jianyuan，HAN Qi.Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm［J］.Journal of Xi’an Jiaotong University，2006，40(1):53-56，61.(in Chinese)

［16］LIANG JJ，QU B Y，Suganthan PN.Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization［R］.Zhengzhou:Zhengzhou University，2013.

［17］Ho S Y，SHU L S，CHEN J H.Intelligent evolutionary algorithms for large parameter optimization problems［J］.IEEE Transactions on Evolutionary Computation，2004，8(6):522-541.

(责任编辑:邢宝妹)

An Im p roved Chicken Swarm Optim ization A lgorithm

KONG Fei，WU Dinghui*
(Key Laboratory of Advanced Process Control for Light Industry，Ministry of Education，Jiangnan University，Wuxi 214122，China)

Considering the problem that the original chicken swarm optimization algorithm easily falls into local optimum because of the premature convergence for high-dimensional comp lex problems，an improved chicken swarm optimization is proposed.In the algorithm，the part of chicks learning from the rooster in their subgroup is added to chick＇s position update equation，and the inertia weight and learning factor are introduced.Then eight benchmark functions are used to test the proposed algorithm and the comparison with the particle swarm optimization，the bat algorithm，and the original chicken swarm optimization is also performed.The simulation experimental results show that the proposed algorithm is able to avoid premature convergence and can escape from local optimum.Especially，the proposed method outperforms other evolutionary algorithms in finding the global optimum for highdimensional problems.

swarm intelligence，hierarchal order，chicken swarm optim ization，benchmark function，complexity analysis

TP 301.6

A

1671－7147(2015)06－0681－08

2015－06－03;

2015－07－21。

国家自然科学基金项目(61572237，61573167);江苏省“六大人才高峰”项目(WLW－008)。

孔飞(1986—)，男，安徽合肥人，控制工程专业硕士研究生。

*通信作者:吴定会(1970—)，男，安徽合肥人，副教授，硕士生导师，工学博士。主要从事智能调度技术等研究。Email:wh033098@163.com