机械臂遥操作系统的时延补偿自抗扰控制
金俊凯,俞立,张文安
(浙江工业大学信息工程学院,浙江杭州 310023)
机械臂遥操作系统的时延补偿自抗扰控制
金俊凯,俞立*,张文安
(浙江工业大学信息工程学院,浙江杭州 310023)
遥操作系统的通信环节中不可避免地存在通信时延导致系统不稳定和操作性能降低等问题,为了减小甚至消除时延的影响,针对单自由度机械臂遥操作系统,提出结合自抗扰控制方法和Smith预估器的新型时延补偿和控制方法。在从机械臂端采用PID控制器实现位置跟踪控制,在主机械臂端采用带Smith预估器的自抗扰控制器,实现时延补偿和对操作力的跟踪,最终保证整个闭环系统的稳定性。最后通过仿真和频域分析验证了所设计控制器的有效性。
遥操作;机械臂;时延;自抗扰控制;Smith预估器
遥操作机器人的出现使得人类可以完成在难以接近和危险环境中的复杂作业,从而在一定程度上扩展了人类的感知和操作能力,保证了人类安全[1]。目前,遥操作机器人系统已被广泛应用在空间探索、深海开发、军事、核工业和医疗等各个领域,具有重要的用途和广阔的应用前景。但是,随着遥控距离的增加,通信环节的时间延迟是不可忽略的一个重要问题。在遥操作系统中,时延是导致遥操作性能降低、影响系统透明性和稳定性的根本原因[2]。
目前遥操作机器人系统的控制方法主要包括预测控制、远程规划和双边控制3种,而其中双边控制又包括无源控制[3]、鲁棒控制[4]与四通道控制[5]等方法。但这种分类方法不是绝对的,如在双边控制结构中也可以使用预测控制[6]。在已有解决时延问题的众多方案中,Smith预估器由于其设计简单,调试方便,成为解决遥操作机器人时延问题的主要方法之一[7]。如Ganjefar将Smith预估器与波变量方法相结合用于遥操作系统中,以克服波变量无法解决的跟踪误差问题[8]。Munir也将波变量和Smith预估器相结合,并对引入的Smith预估器进行改进,加入了卡尔曼估计器和一个能量调节器,在波变量传输保证稳定性的基础上增强系统的操作性能[9]。但是,Smith预估器是建立在系统模型精确已知的基础上,如果存在建模误差,则有可能导致系统不稳定。而机械臂模型不可避免地存在模型误差并且在控制过程中存在扰动,很难得到系统较准确的预估模型;同时,遥操作系统的通信环节也可能存在着时延扰动。因此,仅使用Smith预估器不能对遥操作系统的时延问题进行较好地补偿和控制,并保证系统的稳定性。
考虑到自抗扰控制器[10]对模型的不确定性带来的干扰具有较强的抑制能力,文中提出结合自抗扰控制技术和Smith预估器的方法对机械臂遥操作系统进行时延补偿和控制。在主机械臂端使用Smith预估器预测从机械臂状态的基础上,设计自抗扰控制器实现力的跟踪并保证整个闭环系统的稳定性,在从机械臂端用PID控制器进行调节实现位置的无静差跟踪控制。其主要思想是设计Smith预估器对时延进行预估补偿,同时通过设计自抗扰控制器,可较准确地估计模型误差引起的不确定性和其它总和扰动,并对其进行动态线性化补偿,从而降低模型误差和时延摄动对系统性能带来的影响。最后,通过仿真和频域分析验证了所提出方法的有效性。
1 问题描述
考虑一个机械臂遥操作系统,其控制结构如图1所示。操作者在主端对主机械臂进行操作使主机械臂产生一个位置信号,该位置信号经过通信环节到达从端的从机械臂,然后从机械臂跟随主机械臂运动来完成操纵任务;同时环境对从机械臂的反作用力通过通信环节反馈给主机械臂。

图1 遥操作系统的控制结构Fig.1 Con trol structu re of teleoperation system s
图1中Cm(s)和Cs(s)分别表示主端控制器和从端控制器,Gm(s),Gs(s),Ze(s)分别表示主机械臂、从机械臂和环境的模型,并具有如下形式:

其中:xm和xs分别为主从机械臂的位置;Mm和Ms分别为主从机械臂的转动惯量系数;Bm和Bs分别为主从机械臂的黏性摩擦系数;Be和Ke为环境的阻尼和弹簧系数;fh为操作者对主机械臂的作用力;fe为从机械臂和环境的相互作用力;τs和τσ分别为主从机械臂的控制力矩。
注意到遥操作系统的通信环节中存在时延,假设主端到从端的传输时延和从端到主端的传输时延均为固定时延,分别设为Tms和Tsm,文中采用典型的位移-力主从遥操作系统。主端的位移信息xm(t)发送到从端后定义为xds(t),从端力信息fe(t)反馈回主端后定义为fdm(t),考虑时间延迟的影响,可得

正是这些传输时延,影响了系统的稳定性和操作性能。文中目的是分别在主端和从端设计一个控制器,使这一遥操作系统在固定传输时延下能够保持稳定并且具有良好的跟踪性能和透明性。其中,从端控制器Cs(s)在从端用来实现位置跟踪,使从机械臂能够较精确地跟踪主机械臂的运动;主端控制器Cm(s)不仅要保证整个闭环系统的稳定性,同时要使环境受到的作用力能够跟踪操作者的作用力,保证系统具有良好的透明性和操作性。
2 控制器设计
2.1 从端控制器设计
因为从端在本地构成位置闭环控制,从机械臂对主机械臂的位置跟踪独立于主机械臂的控制闭环,所以可以先设计从端控制器Cs(s)实现位置xs对xm的跟踪。如图1可以得到主机械臂输出到从机械臂输出的传递函数为其中,kP,kI,kD分别为比例、积分和微分系数。


2.2 主端控制器设计
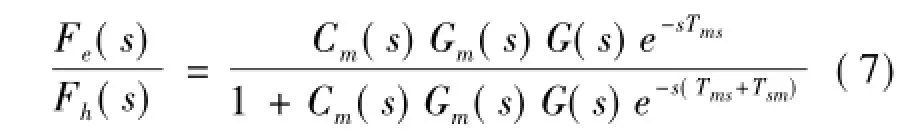
从图1中可以得到整个系统的闭环传递函数为由于这个局部系统的稳定性与传递函数的极点有关,而前向时延在传递函数的分子部分,所以这个前向时延不会对从机械臂控制系统的稳定性产生影响,仅仅是使从机械臂的运动整体落后于主机械臂。因此,为了在从端实现位置的无静差控制,从端控制器可以采用如下的经典PID控制器:
其中,G(s)为从端所有环节的组合,即
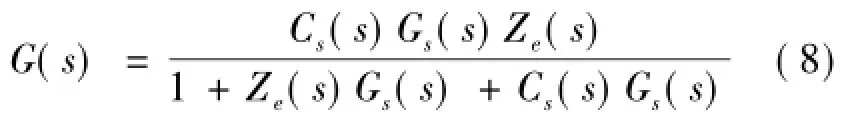
由系统的闭环传递函数(7)可以看出其分母中存在时延环节,这将影响闭环系统的稳定性。因此,设计的主端控制器既需要实现主机械臂对操作力的跟踪,同时还需保证闭环系统的稳定性。
为实现主端控制器良好的跟踪性能,对网络和系统模型不确定性的抗扰能力,文中在主端采用自抗扰控制方法设计跟踪控制器,该控制方法的基本思想是把系统未建模动态和未知外扰作用都归结为对系统的“总和扰动”而进行估计并给予补偿。文中设计的线性自抗扰控制器包括3部分:
1)为主端操作力的参考输入fh安排过渡过程。通过安排过渡过程,一方面可获得作用力的过渡信号v1,解决快速性和超调之间的矛盾,另一方面可获得作用力的近似微分信号v2。过渡过程安排和参考输入微分信号的提取通过如下的线性跟踪微分器(TD)获得
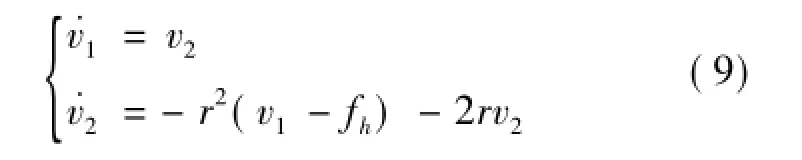
其中,参数r为跟踪微分器的快速因子。
2)设计估计反馈力和总和扰动的线性扩张状态观测器(LESO),其形式如下:
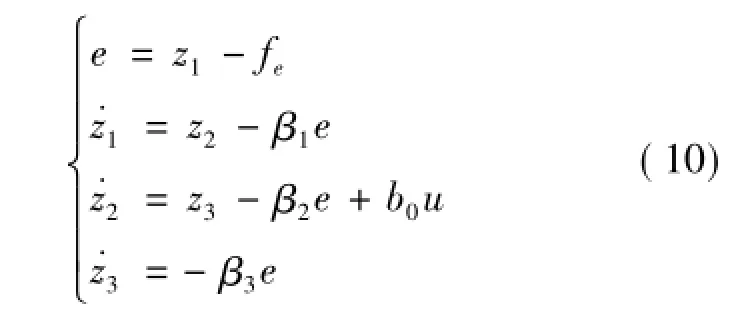
其中:z1和z2分别是对作用力fe及其微分信号的估计值;z3为扩张变量观测量,是对系统总和扰动的估计;β1,β2,β3为一组待整定的参数,参数的选取可以通过极点配置取β=3ω,β=,β=。
1o23
3)设计状态误差反馈控制律。对状态误差采用PD控制律得到的控制量中减去扩张状态观测器估计的总和扰动,当此时得到的控制量作用到主机械臂时可消除总和扰动对系统的影响。该PD控制律为
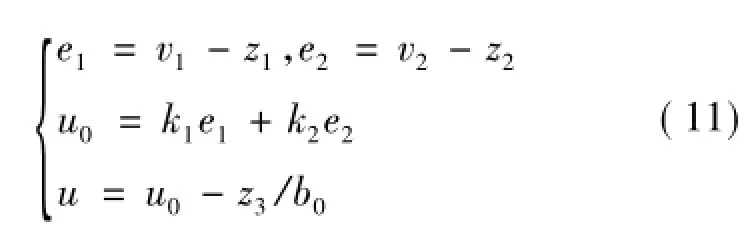
其中,k1和k2分别为比例和微分系数,可以通过极点配置取k1=ω2c,k2=。
仅使用自抗扰控制器只能较好地消除未建模动态和其它外部扰动对系统的影响,但对通信环节存在的较大时延难以有效补偿。此时,考虑将自抗扰控制方法和Smith预估器相结合[12],在主端设计一个Smith预估器对从端行为作预测,从而对时延进行估计并补偿。Smith预估器结构如图2所示。把所有从端环节的组合看作要估计补偿的对象G(s),则可以得到其线性预估模型G^(s),其时延的总和T=Tms+Tsm引起的动态可一起通过Smith预估器进行估计补偿。

图2 Sm ith预估器结构Fig.2 Structure of the Sm ith predictor
图2中,L是对实际时延T的一个近似估计,G^(s)是对对象模型G(s)的一个近似估计:通过Smith预估器可以获得如下预测输出:

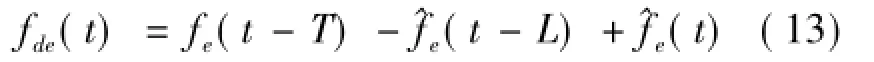
当模型和估计时延与实际系统和真实时延相匹配时,采用Smith预估器可以完全补偿时延影响。因此,基于Smith预估器和自抗扰控制器的遥操作控制系统结构如图3所示。

图3 基于Sm ith预估器和ADRC的遥操作控制系统结构Fig.3 Structu re of the teleoperation system based on the Sm ith p redictor and ADRC
2.3 系统简化
为了方便进一步对系统进行频域分析,可以参考类似文献[11]中的方法,对图3中的闭环控制系统进行简化。将图3中除去自抗扰控制器的部分作为一个整体看做被控对象Gp(s),则


根据式(21),可以将图3表示的整个遥操作控制系统结构简化为如图4所示。
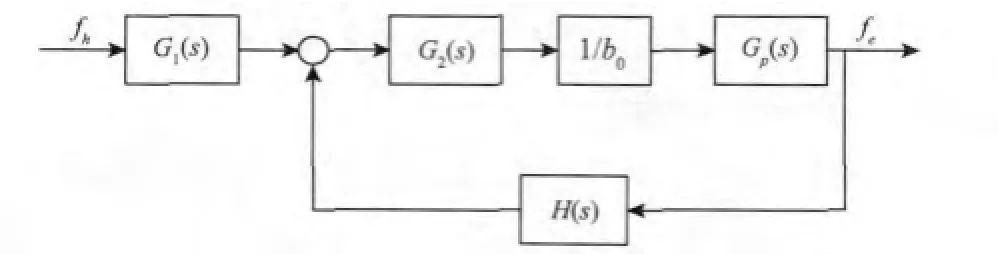
图4 基于Sm ith预估器和ADRC的遥操作系统结构Fig.4 Sim plified diagram of the teleoperation system structu re based on the Sm ith pred ictor and ADRC

3 仿真和频域分析
考虑如式(1)~(3)所示的机械臂遥操作系统,其中系统参数选取如下:
主臂:Mm=1 kg,Bm=1 kg·s/cm;
从臂:Ms=1 kg,Bs=1 kg·s/cm;
环境:Be=1 kg·s/cm,Ke=1 kg·s/cm。从端控制器采用PID控制器,控制器参数为:kP=100,kI=50,kD=10。主机械臂端的自抗扰控制器参数选取为:快速因子r=2.5,控制器带宽ωc= 20,观测器带宽ωo=20,补偿输入系数b0=60。
假设总的网络诱导时延是T=1 s,仿真结果如图5和图6所示。其中,图5(a)显示的是从臂的位置跟踪效果,图5(b)显示的是主臂的力跟踪效果。图6中(a)和(b)分别显示从臂的位置跟踪误差和主臂操作力跟踪误差。从仿真结果可以看出,主从机械臂力和位置的跟踪效果良好,可以无超调而快速地跟踪上参考轨迹,说明所设计的自抗扰控制器和Smith预估器的有效性。只是由于时延的存在,导致从机械臂的位置和力输出约以1 s的时间滞后于主机械臂的位置和力输出信号。同时,由误差曲线可以看出,除了初始时有微小震荡,最终误差都能达到0,实现了力和位置的无静差跟踪。因此,所设计的控制系统在保证系统稳定性的前提下,得到较好的跟踪效果,同时使操作者有较好的力觉临场感。

图5 T=1时主从机械臂跟踪曲线Fig.5 M aster-slave m anipulators tracking cu rves when T=1
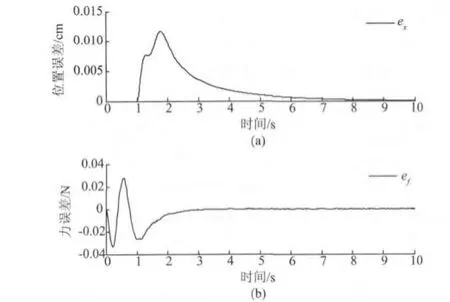
图6 T=1时主从机械臂跟踪误差曲线Fig.6 M aster-slave m anipulators tracking er ror cu rves when T=1
为了说明该方案对Smith预估器模型不匹配问题的良好效果,将转动惯量系数增加20%,但保持原来的Smith预估器模型不变。为了得到更好的观测效果,将主臂延迟后与从臂的信号比较,得到的仿真结果如图7,8所示,分别表示主从机械臂位置和力的跟踪曲线与跟踪误差曲线。可以看出,当Smith预估器模型存在较大误差时仍然可以得到比较好的跟踪效果。
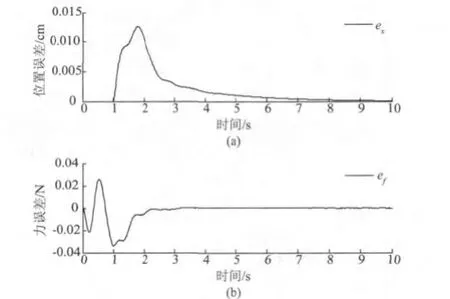
图8 模型不匹配时跟踪误差曲线Fig.8 Tracking error curves when the model does not match
为了进一步说明所设计控制器的抗扰性和鲁棒性,在上述模型误差基础上在通信通道上再加以10%的时延扰动Δt=0.1sin(t),同样将主臂输出延迟后与从臂的信号比较,其仿真结果如图9,10所示。图9中(a)和(b)分别表示位置和力的跟踪效果,图10中(a)和(b)分别表示位置和力的跟踪误差。从仿真曲线中可以看出位置和力跟踪仍然能达到较好的效果;尽管有微小的震荡,但都分别保持在1.5%和5%以内,而且最终都能够较平稳达到设定值,表明该方案对时延摄动具有较强的鲁棒性,能抑制一定程度的时延扰动。

图9 T=1时含时延扰动的主从机械臂跟踪曲线Fig.9 M aster-slave m anipulators track ing curves when T=1 and including time delay disturbance

图10 T=1时含时延扰动的主从手跟踪误差曲线Fig.10 M aster-slave manipu lators track ing er ror curveswhen T=1 and including time delay d istu rbance
最后,为了说明所设计控制器的有效性,再从频域角度对其进行分析。图11为图3所示遥操作系统的闭环频率特性曲线图,即式(22)所表示的闭环传递函数的伯德图。从图中可知,在幅值曲线中不存在峰值,同时可以看出系统具有较大的带宽,表明系统具有较好的平稳性和跟踪速度;同时在高频段有负的斜率,幅值衰减较快,表明系统具有较好的抗干扰性。

图11 遥操作系统闭环频率特性曲线Fig.11 C losed-loop frequency dom ain characteristics of the teleoperation system
4 结语
针对机械臂遥操作系统中的时延问题,将Smith预估器与自抗扰控制方法相结合,使主从机械臂达到力和位置比较精确的轨迹跟踪效果。此方法可以通过Smith预估器估计并补偿通信环节中的时延,同时可以有效地将由Smith预估器模型误差引起的不确定动态用扩张状态观测器进行实时估计并补偿。在仿真过程中加入一定的时延扰动,仍然可以得到较好的控制品质,验证此方法具有良好的抗扰性和鲁棒性。同时,在频域上对系统进行分析,表明系统具有较好的稳定性和动态品质。
[1]HUA C,LIU X P.Delay-dependent stability criteria of teleoperation systems with asymmetric time-varying delays[J].IEEE Transactions on Robotics,2010,26(5):925-932.
[2]Niemeyer G.Telemanipulation with time delays[J].The International Journal of Robotics Research,2004,23(9):873-890.
[3]Chopra N,Berestesky P,Spong M W.Bilateral teleoperation over unreliable communication networks[J].IEEE Transactions on Control Systems Technology,2008,16(2):304-313.
[4]Leung G M H,Francis B A,Apkarian J.Bilateral controller for teleoperators with time delay viaμ-synthesis[J].IEEE Transactions on Robotics and Automation,1995,11(1):105-116.
[5]Hashtrudi-Zaad K,Salcudean S E.Transparency in time-delayed systems and the effect of local force feedback for transparent teleoperation[J].IEEE Transactions on Robotics and Automation,2002,18(1):108-114.
[6]HUANG JQ,Lewis F L,LIU K.A neural net predictive control for telerobots with time delay[J].Journal of Intelligent and Robotic Systems,2000,29(1):1-25.
[7]刘曙光,周宗锡,杨锋.遥操作机器人系统的变时延控制[J].控制工程,2006,13(S0):179-181.
LIU Shuguang,ZHOU Zongxi,YANG Feng.Teleoperation control of an internet-based robotwith varying time delay[J].Control Engineering of China,2006,13(S0):179-181.(in Chinese)
[8]Ganjefar S,Momeni H,Janabi-Sharifi F.Teleoperation systems design using augmented wave-variables and smith predictormethod for reducing time-ddelay effects[C]//Proceedings of the IEEE International Symposium on Intelligent Control.Vancouver,Canada:IEEE,2002:333-338.
[9]Munir S,Book W J.Internet-based teleoperation using wave variables with prediction[J].IEEE/ASME Transactions on Mechatronics,2002,7(2):124-133.
[10]韩京清.自抗扰控制技术-估计补偿不确定因数[M].北京:国防工业出版社,2008.
[11]袁东,马晓军,曾庆含,等.二阶系统线性自抗扰控制器频带特性与参数配置研究[J].控制理论与应用,2013,30(12): 1630-1640.
YUAN Dong,MA Xiaojun,ZENG Qinhan,et al.Research on frequency-band characteristics and parameters configuration of linear active disturbance rejection control for second-order systems[J].Control Theory and Applications,2013,30(12):1630-1640.(in Chinese)
[12]ZHENG Q,GAO Z.Predictive active disturbance rejection control for processes with delay[C]//Proceedings of the 32nd China Control Conference(CCC).Xi’an:IEEE,2013:4108-4113.
(责任编辑:杨勇)
Delay Com pensation Active Disturbance Rejection Control for M anipulator Teleoperation System s
JIN Junkai,YU Li*,ZHANGWenan
(College of Information Engineering,Zhejiang University of Technology,Hangzhou 310023,China)
This paper investigates the delay compensation and control problem for a class of teleoperation systems.Network-induced delays are usually inevitable in teleoperation systems,which may lead to instability and performance degration of the systems.In order to reduce and even elim inate the effect of the time delay on system performance,a novel delay compensation method combining active disturbance rejection controller(ADRC)and Smith predictor is proposed in this paper for manipulators with a single degree of freedom.The PID controller is adopted for position tracking control in the slavemanipulator,while in themaster side,the ADRC controllerwith Smith predictor is app lied for delay compensation and force tracking control as well as guaranteeing stability of the overall closed-loop system.Finally,the simulations and frequency domain analysis are provided to verify the effectiveness of the proposed method.Key w ords:teleoperation,manipulator,time delay,active disturbance rejection control,Smith predictor
TP 242
A
1671-7147(2015)06-0723-07
2015-07-02;
2015-08-14。
国家自然科学基金项目(61273117);霍英东教育基金会项目(141064);浙江省重中之重学科开放研究项目(20141006)。
金俊凯(1991—),男,浙江温州人,控制科学与工程专业硕士研究生。
*通信作者:俞立(1961—),男,浙江富阳人,教授,博士生导师。主要从事网络化、机器人控制等研究。Email:lyu@zjut.edu.cn

