基于KPCA-W LSSVM的公共建筑能耗预测
许巧玲,林跃东,严哲钦
(福州大学节能技术研究中心,福建福州 350108)
基于KPCA-W LSSVM的公共建筑能耗预测
许巧玲,林跃东,严哲钦
(福州大学节能技术研究中心,福建福州 350108)
由于建筑能耗因子间存在非线性和高度冗余特性,传统预测方法很难消除数据之间冗余和捕捉非线性特征,导致预测精度较低。为了提高建筑能耗预测精度,建立了一种基于KPCA-WLSSVM的建筑能耗预测模型。利用核主元分析(KPCA)对输入变量进行数据压缩,消除变量之间的相关性,简化模型结构;进一步采用加权最小二乘支持向量机(WLSSVM)方法建立建筑能耗预测模型,同时结合一种新型混沌粒子群-模拟退火混合优化(CPSO-SA)算法对模型参数进行优化,以提高模型的预测性能及泛化能力。通过将KPCA-WLSSVM模型方法应用于某公共建筑能耗的预测中,并与WLSSVM、LSSVM及RBFNN模型相比,实验结果表明KPCA-WLSSVM模型方法能有效提高建筑能耗预测精度。
建筑能耗;核主元分析;加权最小二乘支持向量机;模拟退火混合优化
随着建筑能耗在我国能源消耗中所占比重的快速增长,建筑节能受到全社会越来越多的关注,准确有效地预测建筑能耗是开展节能评估工作的重要基础,也是进行建筑节能优化设计的主要依据。由于建筑能耗系统涉及到机理复杂的热湿传递过程,是一个典型的多变量、非线性、强耦合和多扰动的复杂系统,采用机理方法建立建筑能耗预测模型十分困难。人工神经网络由于对非线性函数具有很强的拟合和逼近能力,作为一种有效的非线性建模方法,目前已有许多学者将其成功应用于建筑能耗预测领域[1-4]。但是由于神经网络训练基于经验风险最小化原则,易产生过学习导致泛化能力下降,另外还存在诸如网络结构难以确定和过分依赖大样本学习等缺陷,因而在建筑能耗预测领域还难以大范围推广。
以统计学习理论为基础的支持向量机(Support Vector Machines,SVM)[5-6],不仅具有良好的非线性性能和泛化能力,而且与人工神经网络相比具有小样本学习能力强、学习推广性能好以及高维数据处理能力强等特性,目前作为一种新的建模预测方法已在建筑能耗预测领域得到了广泛应用[7-8]。
作为标准SVM的扩展,最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)将SVM的二次规划问题转化为线性方程组求解问题,在保留SVM一般特性的前提下,大大提高了学习速度,较好地解决了大样本数据情况下SVM计算复杂的问题[9]。文献[10]基于LSSVM回归方法建立了建筑空调负荷模型,并获得了较好的预测结果。
针对LSSVM丢失支持向量稀疏性的问题,Suykens等人[11]提出了加权最小二乘支持向量机算法(Weighted Least Squares Support Vector Machines,WLSSVM)。WLSSVM在建模过程中依据训练样本拟合误差分别赋予其不同权重,从而克服了噪声对LSSVM鲁棒性能的影响。文献[12]基于该算法建立了建筑冷负荷预测模型。
尽管支持向量机及其改进算法能够有效处理高维数据建模问题,但是建筑能耗受到气候条件、建筑特征参数、围护结构热工性能、室内热扰、新风负荷、室内环境参数、空调运行模式等众多因素的影响,且各因素之间严重相关,存在大量冗余信息,如果直接使用这些能耗数据用于SVM建模,则会导致模型的预测精度和泛化能力难以达到理想的结果[13-14]。因此,有必要在建立SVM预测模型前先对能耗数据进行特征提取和数据降维,最大限度降低数据中的冗余信息和噪声,提高预测模型的泛化能力。
主元分析(PCA)和核主元分析(KPCA)方法均属于一类用于数据压缩和信息抽取的多元统计分析方法。但是PCA只是一种线性降维技术,它忽略了过程数据中可能存在的非线性信息。然而包括建筑系统在内的绝大多数实际物理过程本质上是非线性的。KPCA是对PCA的非线性扩展,它采用非线性映射对过程数据进行变换,能够有效处理非线性特征提取问题。
为了提高建筑能耗预测模型的精度和可靠性,文中基于KPCA和WLSSVM提出一种公共建筑能耗预测方法。通过机理分析确定建筑能耗主要影响因素的基础上,采用KPCA方法对输入变量进行特征提取,消除变量之间的相关性,降低输入变量的维数,将新的特征信息作为WLSSVM模型的输入变量,从而建立公共建筑能耗预测模型。考虑到LSSVM的正则化参数和核宽参数对模型拟合精度和泛化能力都有较大影响,利用混沌粒子群-模拟退火混合优化(CPSO-SA)算法对LSSVM的参数进行优化选择,进一步提高模型的预测精度和泛化能力。最后对某一公共建筑的能耗进行预测,并与WLSSVM、LSSVM和RBF神经网络的预测结果进行比较,结果表明KPCA-WLSSVM预测模型的性能优于其它3种预测模型。
1 KPCA-WLSSVM模型算法
1.1 核主元分析
通过非线性映射,KPCA方法首先将原空间xi=(i=1,2,…,N)映射到某个高维特征空间,之后再进行主元分析。高维特征空间的协方差矩阵R为

1.2 加权最小二乘支持向量机
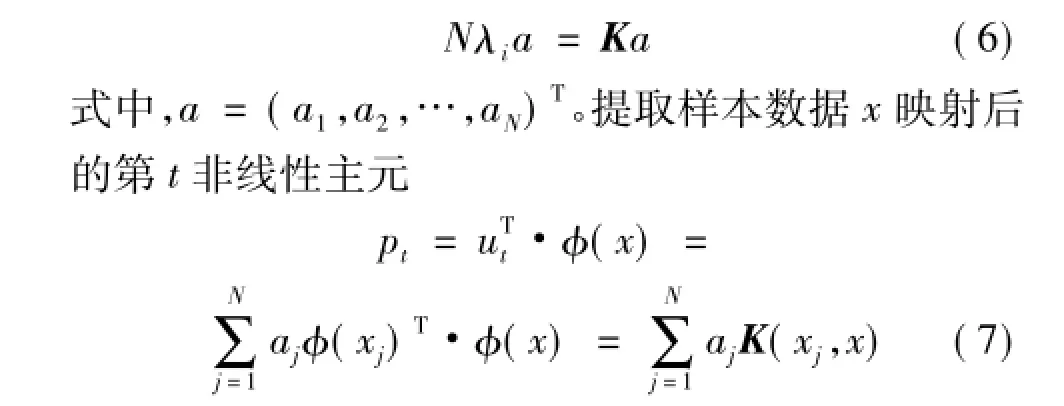
支持向量机是以统计学习理论为基础而发展起来的一种机器学习方法,最小二乘支持向量机(LSSVM)不同于标准支持向量机的地方是它把误差的二范数定义为损失函数,并将不等式约束改为等式约束,其优化问题为[15]

式中:ω为权系数向量;φ(·)为输入空间到高维空间的映射;C为正则化参数;b为阈值。
同时,依据样本训练的重要性分别赋予其不同权重,以改善LSSVM鲁棒性能欠佳的问题。对式(8)中误差的二范数进行加权处理,设的权值为vi,则对应的优化问题变为

1.3 混沌粒子群-模拟退火混合优化算法
标准PSO算法以其简单易行及快速收敛的特性在工程优化领域得到了快速发展,但也存在容易陷入局部最优问题,且搜索速度有待进一步提高。文中提出一种混沌粒子群-模拟退火(CPSO-SA)混合算法用于搜索最佳模型参数,该算法结合了CPSO算法的群体多样性和SA算法的渐进收敛性优点,并保持全局搜索和局部搜索的平衡,可以有效提高算法的搜索效率,从而加快算法的收敛速度。
基于CPSO-SA的参数优化算法流程如下:
1)输入训练样本集{(xi,yi),i=1,2,…,N};设置CPSO-SA算法的控制参数:种群规模m、最大迭代次数tmax,初始温度T=T0,终止温度T=Tend;随机产生m个粒子{p1,p2,…,pm},初始化粒子的位置值和速度值。
2)计算每个粒子适应度值f(pi)。
3)比较当前粒子个体的适应度值,找出当前最优个体pbest,按式(16)的Logistic方程对pbest进行M次迭代,得到混沌变量可行解序列
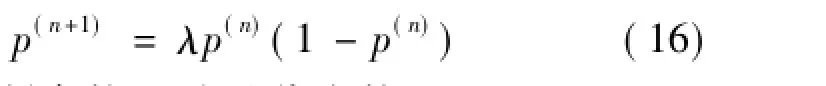
式中:λ为控制参数;n为迭代次数。
4)进行PSO进化操作,即对粒子的速度和位置进行迭代进化,并获得全局最优个体pBEST。
5)进行SA操作,取全局最优个体pBEST的一个领域值,记作best,计算

若Δf<0,则更新pBEST,否则令s=exp(-Δf/T),若s>rand(0,1),则更新pBEST,否则pBEST不变。
6)根据温度下降函数T=T(t),更新温度T,若粒子温度低于终止温度Tend,则算法终止,粒子群全局极值个体参数即为最优参数C*和σ*,否则返回5),进行下一步。
2 基于KPCA-WLSSVM建筑能耗预测
2.1 建筑能耗影响因素分析
建筑能耗系统是一个复杂的非线性系统,影响建筑能耗的因素众多,主要分为4个方面:外部气候条件、围护结构、设备因素以及建筑运行管理模式:
1)外部气候条件是影响建筑能耗的“自然”因素,包括温度、湿度、日照及风速等参数,它们能够直接影响热量通过围护结构的传递,进而对建筑能耗产生影响。
2)围护结构可以看作是影响建筑能耗的“人为”因素,包括反映建筑热工性能的围护结构传热系数、遮阳率等参数和反映建筑体形特征的体形系数、建筑面积、朝向、窗墙比等参数,这类因素可以通过改善建筑本身的热工性能及相关参数对建筑能耗起到积极作用。
3)设备因素,包括照度标准、灯具类型、设备功率等参数,这些参数取决于建筑的使用功能。
4)建筑运行管理模式也是影响建筑能耗的重要因素之一,它包括通风次数、人员密度、设备运行时间、新风指标等参数。
2.2 建模步骤
由于建筑能耗与众多能耗影响因素之间存在复杂的非线性关系,并且能耗因子之间存在强相关性,在建模过程中直接影响能耗模型的预测精度。因此,文中首先利用KPCA提取能耗因子的非线性特征,消除数据冗余并降低模型输入维数,然后采用WLSSVM方法建立能耗预测模型。模型结构如图1所示。

图1 KPCA-W LSSVM建模流程Fig.1 Sketch of KPCA-WLSSVM
考虑到LSSVM算法的正则化参数和核宽参数对模型拟合精度和泛化能力有较大影响[16],文中采用1.3小节所述的CPSO-SA算法在正则化参数C及核宽参数σ的定义域内进行搜索,寻找C和σ的组合最优值。参数优化问题定义如下:其中:yi为第i个已知样本的值;^yi为第i个样本的模型输出值,由预测模型计算获得;J为正则化参数C及核宽参数σ的函数。
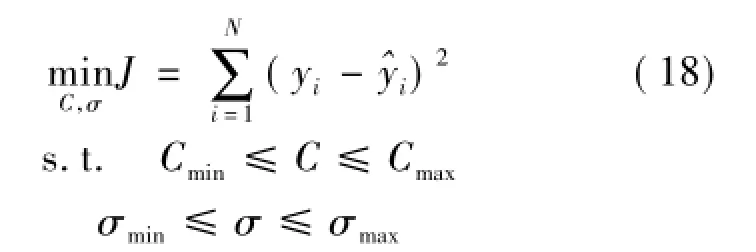
综上所述,基于CPSO-SA优化的KPCAWLSSVM建筑能耗预测模型算法关键步骤总结如下:
1)样本数据归一化处理:为了避免计算出现饱和现象,按式(19)对建筑能耗训练样本进行归一化处理:
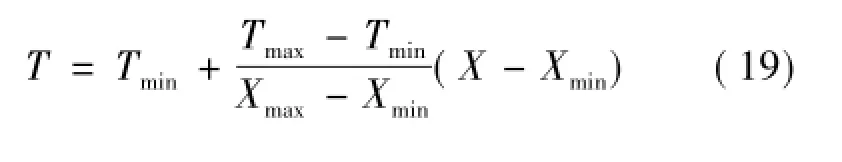
式中:X为原样本数据;Xmax,Xmin分别为样本数据中最大值和最小值;T为目标数据;Tmax为目标数据的最大值,取Tmax=0.9;Tmin为目标数据的最小值,取Tmin=0.1。
2)KPCA特征提取:按式(7)提取主成分,降低样本维数,消除变量之间的相关性。
3)最优模型参数确定:初始化CPSO-SA粒子种群,每个粒子由C和σ组成;根据1.3小节步骤3)~6)获得LSSVM模型的最优参数C*和σ*。
4)基于最优参数C*和σ*,由式(14)求解b,α*,建立WLSSVM建筑能耗预测模型。
6)反归一化:按式(20)对模型输出进行反归一化处理:
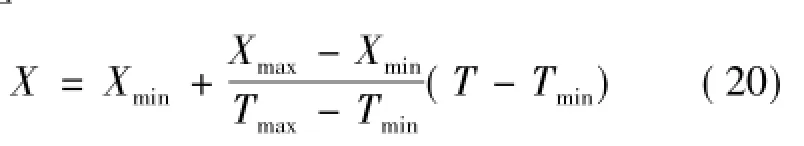
7)模型预测性能评价:采用相对误差绝对值最大值Emax、相对误差绝对值平均值Eave和均方根误差RMSE 3个性能指标对模型进行评价:

式中,N为样本数。
2.3 实例分析
2.3.1 建筑物简介基于南方地区一幢16层的公共建筑,采用文中所提KPCA-WLSSVM方法建立该建筑能耗预测模型。建筑物外形如图2所示。

图2 建筑外形示意Fig.2 Shape of an office building
该建筑总高度为57.4 m,主楼地上16层,地下1层,附楼(裙房)3层。建筑空调运行时间为8:00到17:00,总计每天运行9 h,空调季为6月1日到8月30日。总建筑面积为19 700.5 m2。地上建筑面积17 315.62 m2,地下建筑面积2 384.88 m2,标准层层高3.5 m,外窗尺寸为2.5 m×2.0 m,窗台离地高度0.8 m。
2.3.2 构造样本集根据能耗影响因素分析,结合《公共建筑节能设计标准》相关规定,文中在对公共建筑能耗建模过程中,主要考察以下能耗因子:最低照度(x1),灯光热扰(x2),温度(x3),湿度(x4),设备热扰(x5),电热转换率(x6),人均新风指标(x7),家具系数(x8),外墙传热系数(x9),内墙传热系数(x10),玻璃遮阳系数(x11),玻璃传热系数(x12),通风次数(x13)[17]。
同时为减少试验次数,并保证试验的全面性,采用正交试验方法获取数据样本集。DEST中影响因素的取值采用事先设定好的水平值,每个因素选取3个水平值,选用L27(313)正交表进行试验计算,建筑物能耗的基准值采用动态负荷计算软件DEST-C的计算值。为获得较为理想的训练数据,文中选用4组正交试验,并且每组正交试验中每个因素选取不同的水平值,经过DEST-C动态计算,获得建筑物全年能耗结果。经DEST-C计算获108组实验数据,随机取其中的3/4作为训练样本,余下的1/4作为测试样本验证模型的预测性能。
2.3.3 模型训练通过KPCA计算,取主元个数为7个,此时累计贡献率已经超过90%。碎石图如图3所示。另外,核参数和正则化参数是WLSSVM性能的重要影响因素,不同的参数组合将得到不同的学习性能和泛化性能。
为避免主观经验选取的盲目性,文中采用CPSO-SA算法对模型的两个参数进行寻优,优化后的参数分别为C=378.3,σ=0.9,满足预测模型对精度的要求,建筑能耗模型训练结果如图4所示,拟合值和期望值基本吻合。

图3 核主成分碎石Fig.3 Scree plot of the kernel p rincipal component
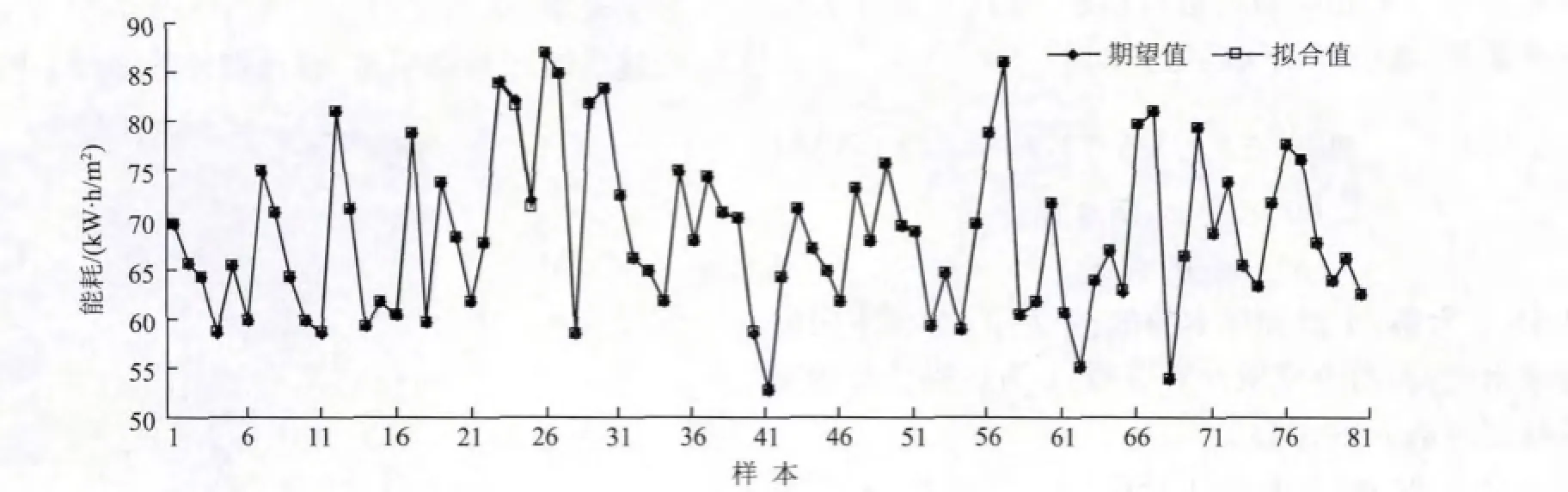
图4 KPCA-W LSSVM模型训练结果Fig.4 T raining resu lts of KPCA-W LSSVM
2.3.4 结果与分析为比较分析组合模型的预测效果,文中同时建立了LSSVM、WLSSVM和RBFNN神经网络模型对建筑能耗进行预测。通过Matlab平台实现上述4种预测模型对建筑能耗进行预测,预测值和实际值的对比如图5所示。从图中可以知道,4种模型的预测结果大都能够反映能耗的变化,但有个别样本点偏差较大,组合模型的预测值和期望值基本重合,相比于单一的LSSVM、WLSSVM和RBFNN神经网络模型,组合预测模型的预测效果较好。
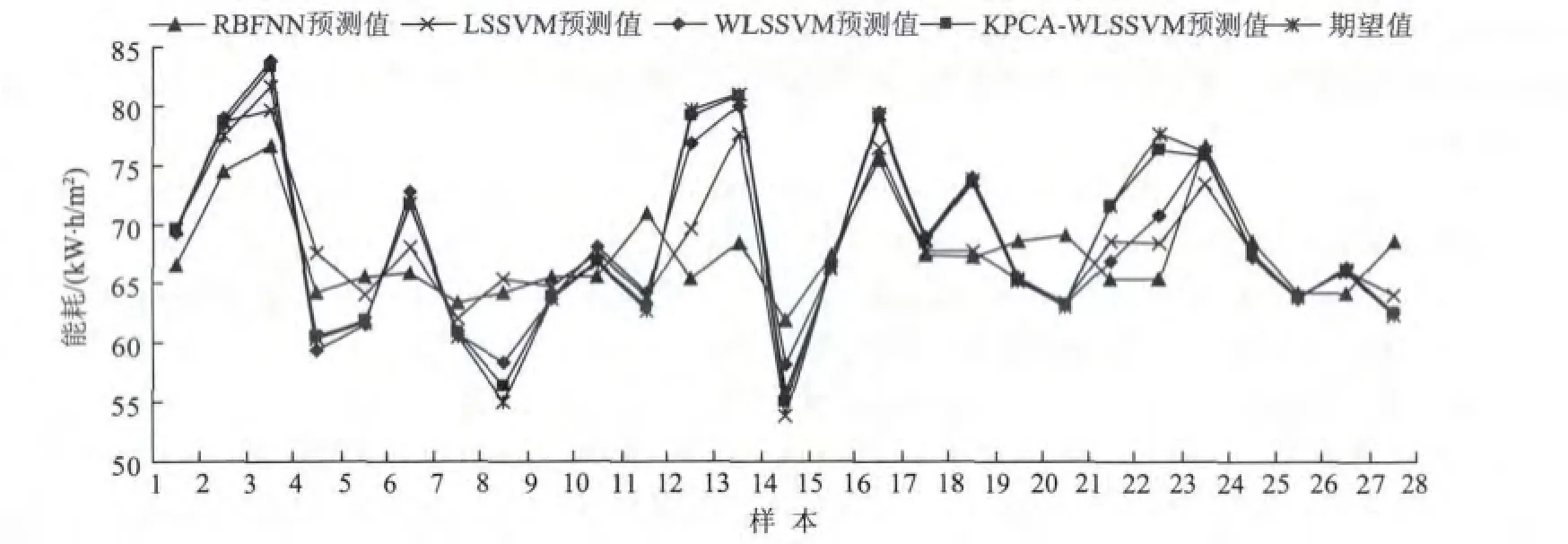
图5 4种模型的预测结果Fig.5 Prediction of four models
为了从整体上评价4种预测模型的预测精度和稳定性,按式(21)、(22)及(23)对上述4种模型进行评价,4种模型预测结果的Emax,Eave,RMSE如表1所示。

表1 4种模型评价指标计算结果Tab.1 Prediction of four models
从表1的计算结果可以看出,采用RBF神经网络和LSSVM方法预测虽然具有很高的训练精度,但是当其用于预测时,误差较大,泛化性能差,预测效果不理想;采用WLSSVM进行预测,平均预测误差和均方根误差比LSSVM有所降低,但预测效果仍有待提高。经过KPCA处理后,WLSSVM模型的预测效果得到了很大改善,最大相对误差绝对值从8.84%降到2.98%,相对误差绝对值平均值从1.43%降低到0.94%,表明组合模型具有更高的预测精度和预测稳定性,泛化能力得到显著提高。
通过对比分析模型的性能指标,结果表明KPCA-WLSSVM模型具有更好的预测效果,是一种有效、可行的建筑能耗预测方法。
3 结语
在上述建筑能耗预测实例中,通过4个模型的预测结果及性能评价指标的比较可以看出,基于KPCA-WLSSVM能耗预测模型的预测效果要优于其它3种模型,表明KPCA-WLSSVM模型在建筑能耗预测中的有效性和优越性。主要结论如下:
1)通过KPCA提取输入样本的特征信息,消除建筑能耗影响因素间的冗余性和共线性,简化模型的输入样本。
2)采用混沌粒子群模拟退火混合优化算法对模型的参数进行优化选择,进一步提高建筑能耗预测模型的学习精度和推广应用能力。
3)采用WLSSVM模型方法充分考虑了样本对建模的影响,通过赋予建模样本合适的权值,优化了LSSVM模型性能,使得模型具有良好的非线性处理能力。
通过KPCA方法与WLSSVM模型的有机结合,为建筑能耗预测提供了一种更为准确的途径,为实现建筑节能分析打下了良好基础。
[1]WONG S L,WAN K K W,Lam T N T.Artificial neural networks for energy analysis of office buildings with daylighting[J].Applied Energy,2010,87(2):551-557.
[2]Azadeh A,Ghaderi S F,Tarverdian S,et al.Integration of artificial neural networks and genetic algorithm to predict electricalenergy consumption[J].Applied Mathematics and Computation,2007,186(2):1731-1741.
[3]喻伟,李百战,杨明宇,等.基于人工神经网络的建筑多目标预测模型[J].中南大学学报:自然科学版,2012,43(12): 4950-4955.
YUWei,LIBaizhan,YANGMingyu,et al.Buildingmulti-objective predictingmodel based on artificial network[J].Journal of Central South University:Science and Technology,2012,43(12):4950-4955.(in Chinese)
[4]Mathieu JL,Price P N,Kiliccote S,et al.Quantifying changes in building electricity use,with application to demand response[J].IEEE Transactions on Smart Grid,2011,2(3):507-518.
[5]Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer,2000.
[6]Cortes C,Vapnik V.Support vector networks[J].Machine Learning,1995,20(3):273-297.
[7]DONG Bing,CAO Cheng,Lee SE.Applying support vectormachines to predict building energy consumption in tropical region[J].Energy and Buildings,2005,37(5):545-553.
[8]LIQiong,MENG Qinglin,CAI Jiejin,et al.Applying support vector machine to predict hourly cooling load in the building[J].Applied Energy,2009,86(10):2249-2256.
[9]Suykens JA K,Van G T,De B J,etal.Least Squares Support Vector Machines[M].Singapore:World Scientific,2002.
[10]LIXuemei,SHAO Ming,DING Lixing,et al.Particle swarm optimization-based Ls-Svm for building cooling load prediction[J].Journal of Computers,2010,5(4):614-621.
[11]Suykens J A K,De Brabanter J,Lukas L,et al.Weighted least squares support vector machines:robustness and sparse approximation[J].Neurocomputing,2002,48(1/4):85-105.
[12]GUO Yin,Nazarian E,Ko J,et al.Hourly cooling load forecasting using time-indexed arx models with two-stage weighted least squares regression[J].Energy Conversion and Management,2014,80:46-53.
[13]LIQiong,MENGQinglin,CAIJiejin,etal.Predicting hourly cooling load in the building:a comparison of support vectormachine and different artificial neural networks[J].Energy Conversion and Management,2009,50(1):90-96.
[14]Crawley D B,Hand JW,Kummert M,et al.Contrasting the capabilities of building energy performance simulation programs[J].Building and Environment,2008,43(4):661-673.
[15]Suykens JA K.Least squares support vectormachines[J].Neural Processing Letters,1999,9(3):293-300.
[16]樊晓雪.最小二乘支持向量机的参数选择[D].保定:河北大学,2012.
[17]康一亭,于丹,苏华,等.办公建筑能耗基准中影响因子对建筑能耗的影响度[J].中南大学学报:自然科学版,2012,43 (S1):146-150.
KANG Yiting,YU Dan,SU Hua,et al.Impact factors of energy consumption benchmarking in office buildings[J].Journal of Central South University:Science and Technology,2012,43(S1):146-150.(in Chinese)
(责任编辑:杨勇)
Prediction for Energy Consum ption of Public Building Based on KPCA-W LSSVM
XU Qiaoling,LIN Yuedong,YAN Zheqin
(Research Center of Energy Saving Technology,Fuzhou University,Fuzhou 350108,China)
There are highly redundant features in affecting factors of building energy consumption,and the traditional method has low preditive accuracy.In order to improve the accuracy of building energy consumption forecasting,A predictionmodel based on KPCA-WLSSVM is proposed to forecast building energy consumption.The kernel principal component analysis(KPCA)method could not only solve the linear correlation of the input and compress data but also simply the model structure.A novel hybrid chaos particle swarm optimization simulated annealing(CPSO-SA) algorithm is applied to optimize theWLSSVM parameters to improve the learning performance and generalization ability of themodel.Furthermore,the KPCA-WLSSVM model is app lied to the energy consumption prediction for an office building,and the simulation results show that the KPCA-WLSSVM has better accuracy compared with WLSSVM model,LSSVM model and RBF neural network model,which is considered that the KPCA-WLSSVM is effective for building energy consumption prediction.
energy consumption of building,kernel principal component analysis,WLSSVM,CPSO-SA
TU 111.19+5
A
1671-7147(2015)06-0710-07
2015-08-18;
2015-10-16。
国家自然科学基金项目(60804027,61374133);福州大学科研基金项目(FZU-022335,600338,600567);高校博士点专项科研基金项目(20133314120004)。
许巧玲(1956—),女,福建福州人,教授,硕士生导师。主要从事过程优化、最优控制研究。
Email:zhhqxu@163.com

