液压型风力发电机组最优功率追踪控制方法研究

艾 超， 孔祥东， 闫桂山， 廖利辉

（1.燕山大学 河北省重型机械流体动力传输与控制实验室，河北秦皇岛066004；2.燕山大学 先进锻压成型技术与科学教育部重点实验室，河北秦皇岛066004）

风能作为可再生能源发展的一个重要方向，具 有蕴藏量丰富、分布广、可再生和无污染等优点，风力发电产业也因此迅速发展［1］.使风力发电机组最大量地将风能转化为电能并稳定运行的技术，称为最优功率追踪控制［2］，是风力发电技术的一个重要研究方向.

液压型风力发电机组（以下简称液压型机组）作为新型机型，采用定量泵－变量马达柔性传动与励磁同步发电机配合，减小了风力发电机组机舱质量，提高了发电质量，降低了对电网的冲击［3］.

为提高风力发电机组捕获风能的能力，液压型机组与传统风力发电机组一样，需要实现最优功率追踪控制.针对风力发电机组最优功率追踪控制，国内外学者展开了一系列研究［4－5］.双馈异步风力发电机组和永磁直驱风力发电机组作为传统机型，均通过控制变流逆变装置实现最优功率追踪控制［6－7］，具体实现方法可分为3类［8－9］，即叶尖速比法（TSR）、功率信号反馈法（PSF）和爬坡搜索法（HCS）.液压型机组与传统风力发电机组最重要的区别是省去了变流逆变装置，而变流逆变装置是传统机型中整个风力发电系统的直接调节装置.因此，液压型机组最优功率追踪控制方法与传统机型存在一定差别.针对由变量泵－变量马达组成的液压型机组最优功率追踪控制系统，韩利坤［10］提出通过调整变量泵和变量马达排量分别控制风力机的角速度和发电功率，实现最优功率追踪控制.

目前鲜见针对由定量泵－变量马达组成的液压型机组最优功率追踪控制系统的相关文献，其控制机理与实现方法尚不明确，未形成成熟的研究体系.因此，有必要对液压型机组最优功率追踪控制方法展开研究.

1 液压型机组数学模型分析

1.1 风力机特性数学模型

为实现不同风速下风力机恒稳定于最优功率，风力机需工作在最佳角速度下.依据风力机工作原理，建立输出功率－角速度和气动转矩－角速度特性数学模型，风力机从风能中捕获的功率P（即输出功率）和风力机输出气动转矩T 分别为［11－12］：

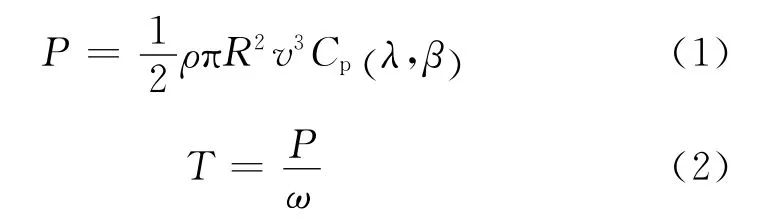
式中：Cp（λ，β）为风能利用系数，是叶尖速比λ 和桨距角β 的函数，表示风力机吸收的机械能与通过风力机旋转面的全部风能的比值；R 为叶片半径，m；v为风速，m／s；ρ为气流密度，kg／m3；ω 为风力机角速度，rad／s.

一定风速下风力机输出气动转矩和功率的变化规律如图1 所示，图中，ω＊为风力机最优角速度，rad／s；Tmax为风力机最优气动转矩，N·m；Pmax为力机最优输出功率，W.二者的变化规律主要取决于Cp（λ，β）［13］.

图1 风力机输出特性曲线Fig.1 Characteristic curves of the wind turbine output

1.2 液压型机组主传动系统数学模型

图2 为液压型机组定量泵－变量马达主传动系统原理图［14］.

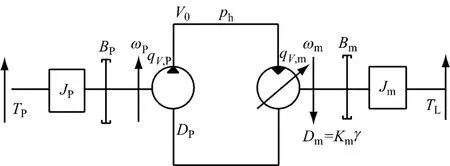
图2 液压型机组主传动系统原理简图Fig.2 Principle diagram of the main transmission system for hydraulic wind turbine

建立主传动闭式系统数学模型，变量马达角速度的传递函数为

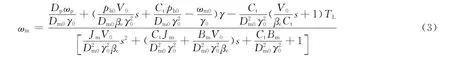
变量马达输出功率的传递函数为

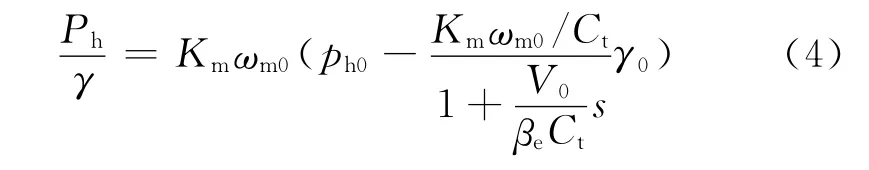
式中：ωp为为定量泵的角速度，rad／s；ωm为变量马达的角速度，rad／s；Dp为定量泵排量，m3／rad；γ 为变量马达机构摆角，100%；γ0为变量马达机构初始摆角，100%；Dm0为变量马达初始排量，m3／rad；V0为单个腔室的总体积，m3；ph0为调节变量马达时高压管路初始压力，Pa；ωm0为变量马达初始角速度，rad／s；βe 为有效体积弹性模量，Pa；TL为变量马达轴上的任意外负载力矩，N·m；Bm为变量马达黏性阻尼系数，N·s／m；Jm为变量马达和负载的总惯量，kg·m2；Km为变量马达排量梯度，m3／rad；Th为变量马达输出转矩，N·m；Ph为变量马达输出功率，W；Ct为总泄漏系数，m3／（s·Pa）.

2 液压型机组风力机角速度控制方法

风速变化时，液压型机组实现最优功率追踪控制的实质是控制风力机的角速度，使其快速达到最优角速度.液压型机组工作时，对风力机受力进行分析，如图3所示.

风力机动力学方程为

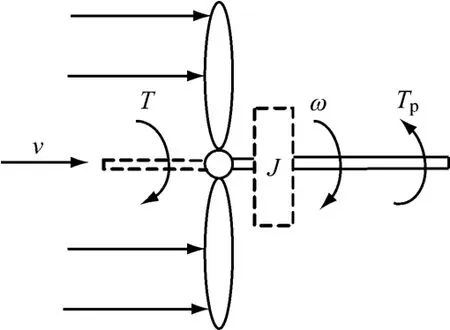
图3 风力机受力示意图Fig.3 Force diagram of the wind turbine

式中：Tp为定量泵转矩，N·m；J 为风力机等效转动惯量，kg·m2；α为风力机角加速度，rad／s2.

风力机角速度控制的核心在于通过控制定量泵转矩，使风力机在一定风速和气动转矩下具有特定的角加速度，从而实时控制风力机角速度.

笔者提出一种变步长的最优功率追踪控制方法，其控制框图如图4所示.其控制思想为：通过检测风力机角速度和发电功率，与已知的风力机输出功率特性曲线对应的角速度和功率值进行比较，并判断运行区间，根据不同的运行区间对给定功率的大小进行调节，以此来间接控制风力机的角速度，从而实现最优功率追踪.实现方法为：通过控制发电功率实现风力机角速度的间接控制，系统通过实时检测风力机角速度、风速和发电功率，依据目标风力机角速度确定功率给定值.

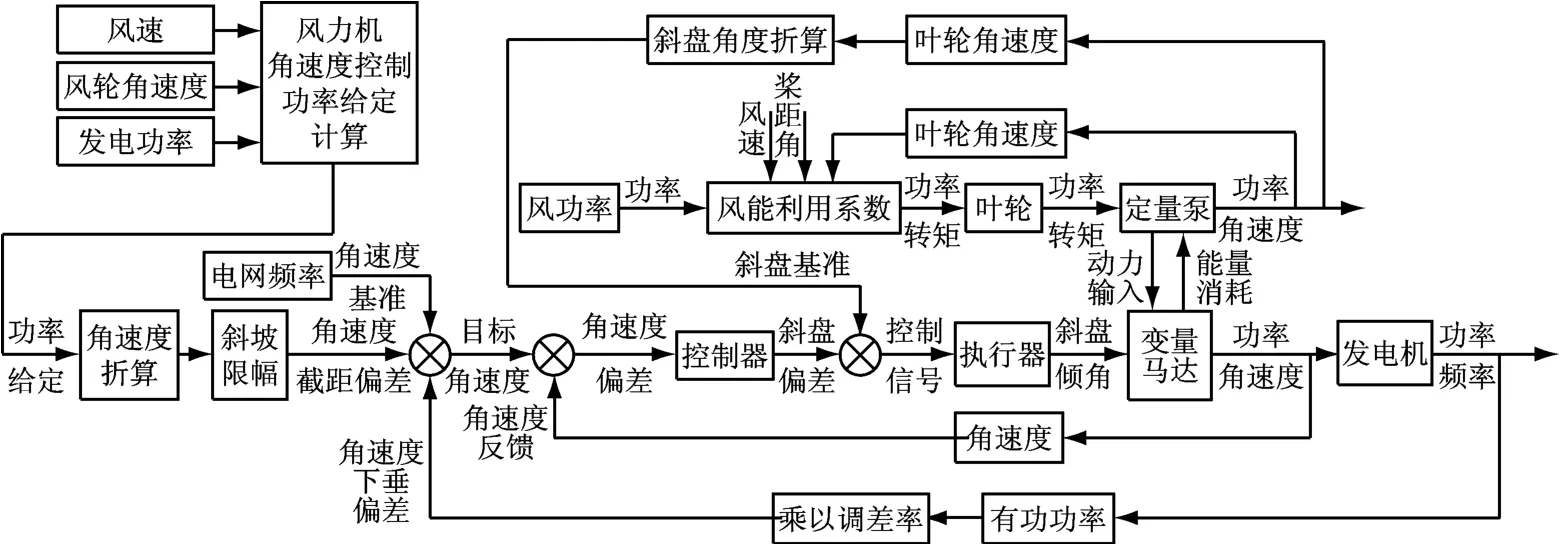
图4 最优功率追踪控制框图Fig.4 Diagram of the MPPT control

如图5所示，在一定风速下，风力机可能的运行工作点一共有7个，其中B、D、F为风力机稳定运行工作点，C、E 为风力机减速旋转工作点，A、G 为风力机加速旋转工作点.

风力机最优功率追踪控制的目标轨迹如图6所示，假设发电机在工作点A 并网，则风速变化过程为v1v3v2v1，风力机实现最优功率追踪控制的工作点调整轨迹为AB1C3D2E1.

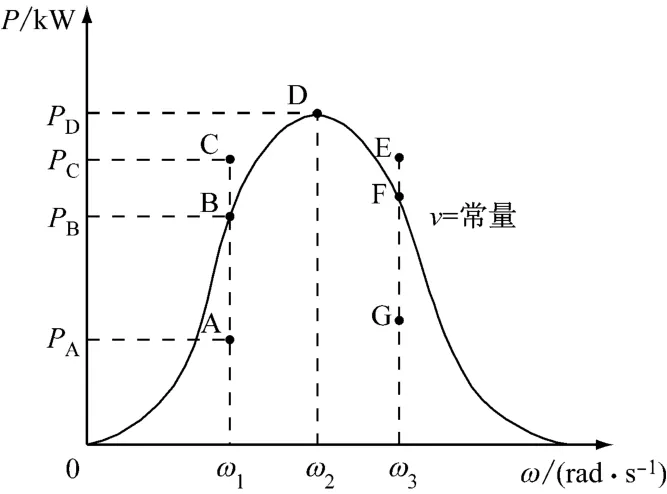
图5 风力机可能的运行工作点Fig.5 Possible operating points of the wind turbine

图6 风力机最优功率追踪控制的运行轨迹Fig.6 Running trajectories of the wind turbine

3 液压型机组最优功率追踪控制方法

在一定风速下，设风力机最优角速度为ω＊，风力机实际角速度记为ω，则二者的差值为Δω＝ω＊－ω.如图7所示，风力机可工作区域共5个，分别位于风力机输出功率特性曲线与最优角速度处虚线分割的A、B、C、D 4个区域及以功率最高点为圆心、δ为半径的圆中.

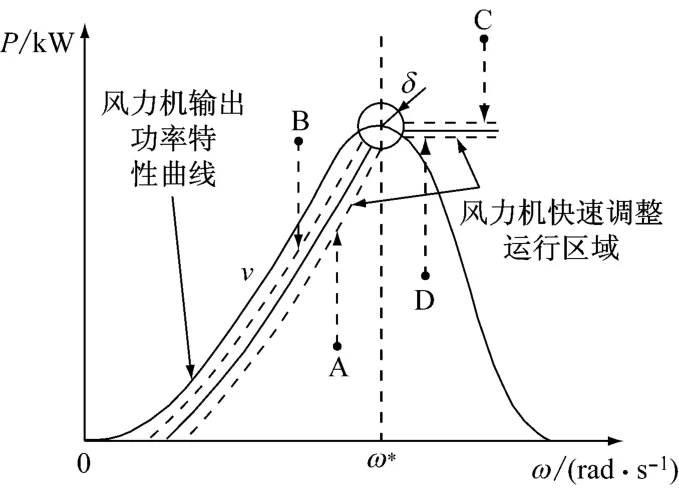
图7 风力机快速调整运行区Fig.7 Rapid adjustment area of the wind turbine

在变步长最优功率追踪控制方法中，风力机最优功率追踪可分为快速调整和慢速调整2个阶段.

当｜Δω｜＞δ时，风力机处于快速调整阶段，机组迅速接近最优功率点，基本控制思想如下：风力机运行于A、B、C、D 区域时，通过功率控制，使风力机工作点近似垂直地进入快速调整运行区域.根据在线检测的风力机角速度及风速理论计算快速调整运行区域，并利用风力机角加速度对其中心线实施在线修正.

当｜Δω｜≤δ时，风力机处于慢速调整阶段，机组缓慢平稳接近最优功率点，基本控制思想如下：如图8所示，风力机慢速调整区域由区域1、区域2、区域3、区域4和一条角速度功率曲线组成，在慢速调整阶段，根据不同区域的运行工况设定风力机发电功率调整值，进而实现最优功率追踪控制.

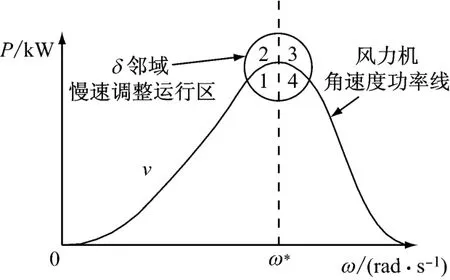
图8 风力机慢速调整运行区Fig.8 Slow adjustment area of the wind turbine

当风力机工作于区域1和区域4时，风力机加速旋转；当风力机工作于区域2和区域3时，风力机减速旋转；当风力机工作于角速度功率曲线上时，风力机保持角速度不变.

变步长最优功率追踪控制方法的发电功率调整值符号判断方法见图9.

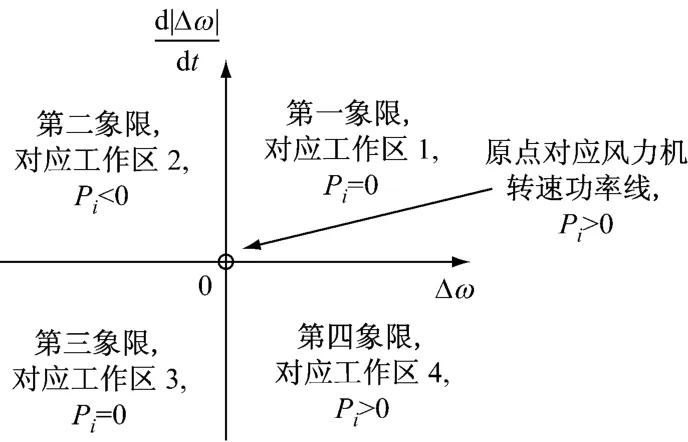
图9 慢速调整区域风力机功率给定符号Fig.9 Given symbol of power in slow adjustment area of the wind turbine

风轮角速度增大、旋转加速度变大时，风力机运行于图9所示的第一象限，对应图8所示的区域1，此时不调整发电功率，风力机向区域4运动.

风轮角速度减小、旋转减速度变大时，风力机运行于图9所示的第二象限，对应图8所示的区域2，此时发电功率调整值给定为负，发电功率降低，风力机向区域1运动.

风轮角速度减小、旋转减速度变小时，风力机运行于图9所示的第三象限，对应图8所示的区域3，此时不调整发电功率，风力机向区域2运动.

风轮角速度增大、旋转加速度变小时，风力机运行于图9所示的第四象限，对应图8所示的区域4，此时发电功率调整值给定为正，发电功率增加，风力机向区域2运动.

风轮角速度不变、旋转加速度为零时，风力机运行于图9所示的原点，对应图8所示的角速度功率曲线，此时应提高发电功率，发电功率调整值给定为正值.

当风力机处于慢速调整区时，在不同区域风力机追踪最佳功率的过程如图10所示.图10（a）～图10（d）分别为风力机运行于图8所示的区域1～区域4时的最优功率追踪过程.由图10可知，风力机连续2次进入区域4即完成最优功率追踪.

4 液压型机组最优功率追踪控制仿真实验

依据液压型机组最优功率追踪控制原理，搭建30kVA 液压型机组实验平台，基于该实验平台建立液压型机组最优功率追踪控制仿真模型，仿真参数源于实际的物理系统.实验平台整体结构如图11所示.

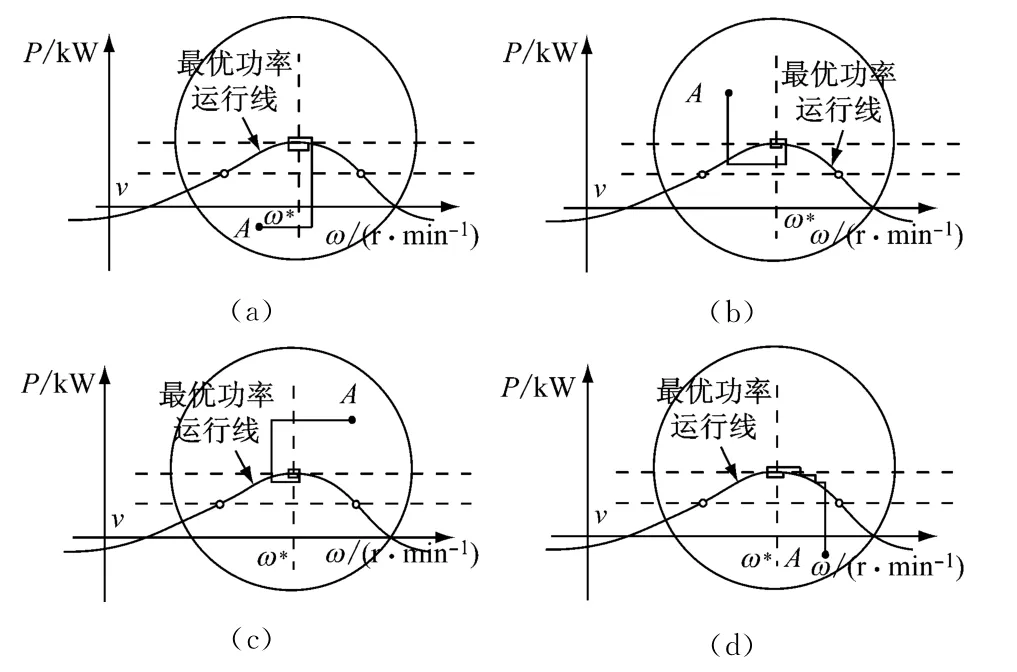
图10 慢速调整阶段最优功率追踪典型轨迹Fig.10 Typical MPPT trajectory in slow adjustment phase

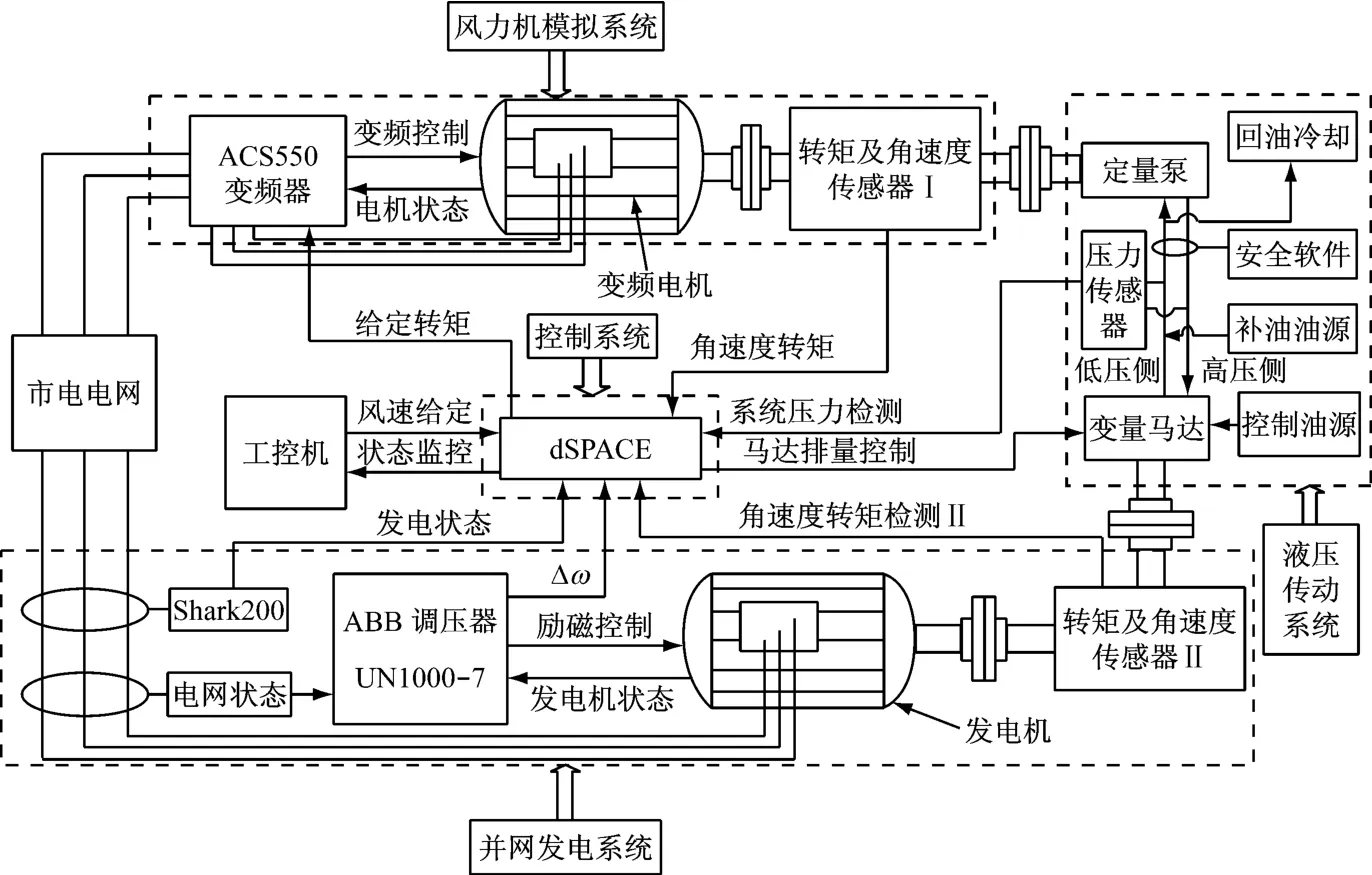
图11 实验平台结构图Fig.11 Structural diagram of the experimental platform

实验平台分为控制系统、并网发电系统、液压传动系统和风力机模拟系统4部分.其工作原理为：变频器控制变频电机驱动定量泵转动，变量马达输出轴与发电机刚性连接，驱动发电机以同步角速度运行，实现并网发电.液压型机组最优功率追踪控制实验平台实物图如图12所示.

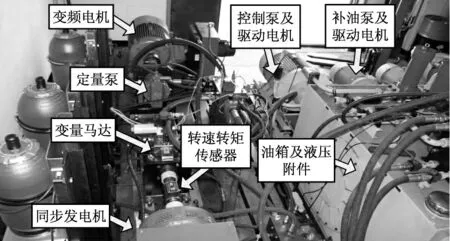
图12 实验平台液压系统实物图Fig.12 Hydraulic system of the experimental platform

4.1 液压型机组最优功率追踪控制实验与仿真

4.1.1 风力机特性模拟实验

采用相似理论模拟风力机特性，实验方案原理如图13所示.风力机特性模拟实验台实现相似模拟，应具备以下3个相似条件：（1）风能利用系数相同；（2）功率相似；（3）转动惯量相似.相似系数为真实量与模拟量的比值，其中模拟量参数下标带有字母“S”，真实量参数无下标，KR为半径系数，Kλ为叶尖速比系数，KPG为功率系数，Kω为角速度系数，则有

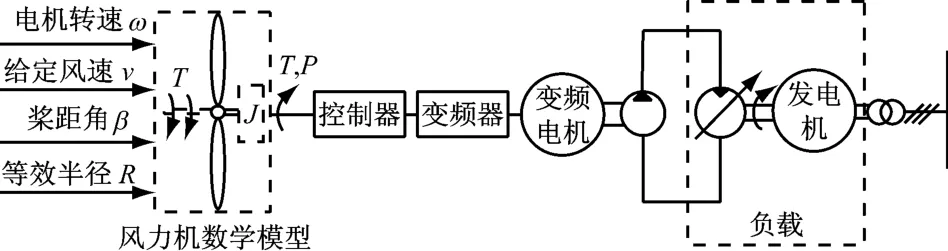
图13 风力机特性模拟实验方案Fig.13 Experimental program for characteristic simulation of the wind turbine

根据相似模拟条件（1）有

根据相似模拟条件（2）有

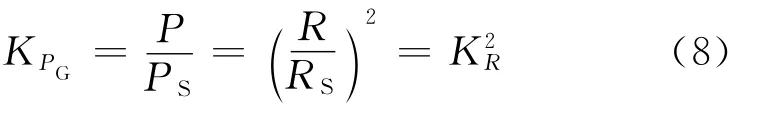
相似模拟实验中等效风能利用系数CpS为：

由相似模拟实验可得模拟风力机的气动转矩和输出功率数学模型，分别如式（10）和式（11）所示.图14为模拟风力机气动转矩和输出功率特性曲线.

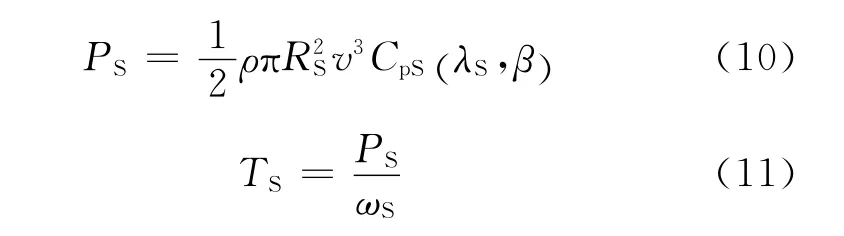
4.1.2 液压型机组最优功率追踪控制仿真模型

采用联合仿真技术，基于Matlab／Simulink 和AMESim 软件搭建仿真平台，包括风速模拟模块、风力机特性模拟模块、最优功率追踪模块、软件接口模块、主控制器模块和同步发电机并网控制模块，如图15所示.

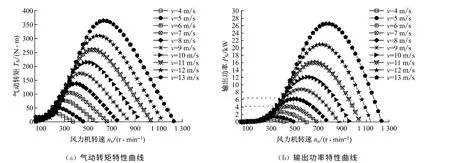
图14 模拟风力机输出特性曲线Fig.14 Simulated characteristic curves of the wind turbine

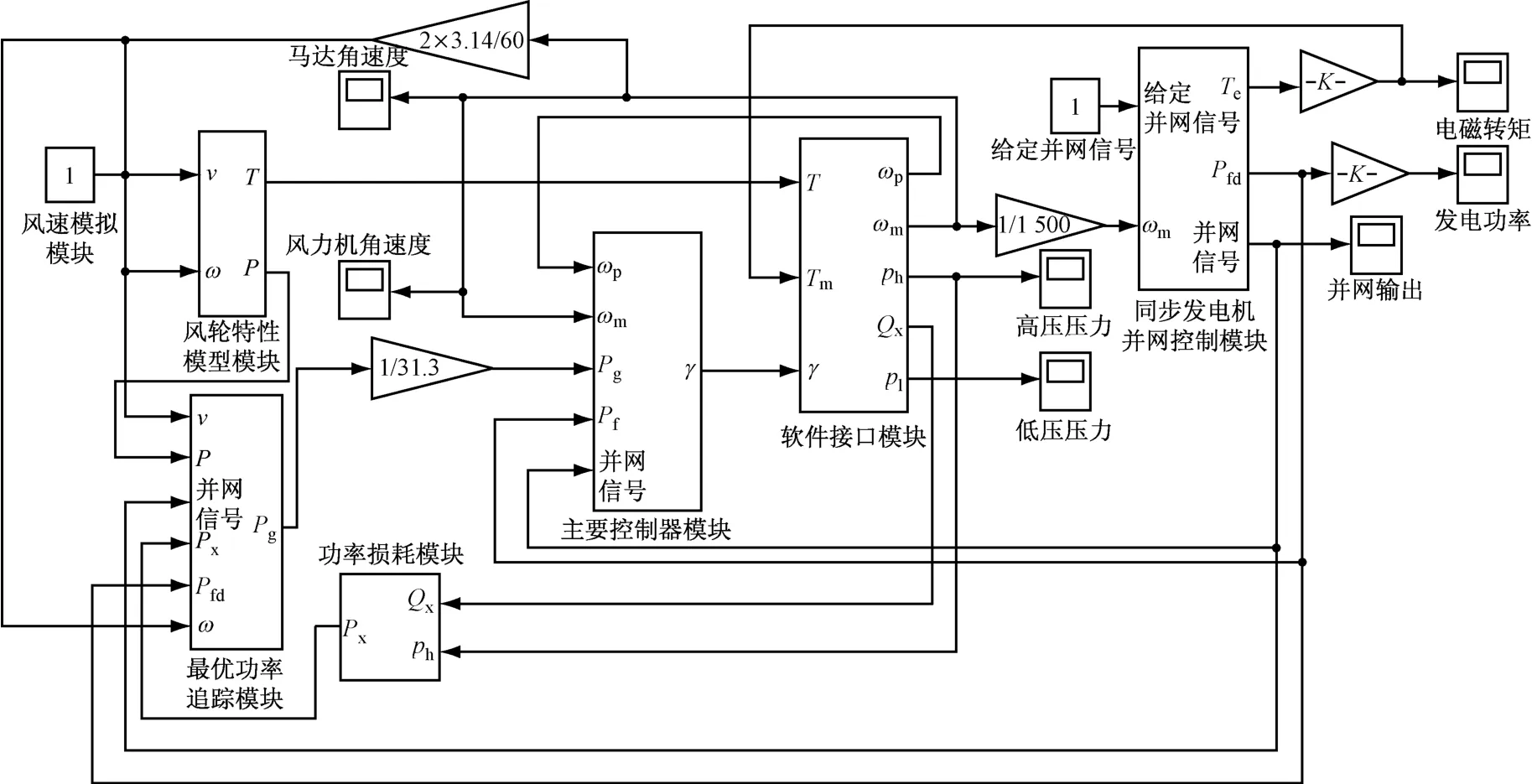
图15 液压型机组最优功率追踪控制仿真平台Fig.15 Simulation platform for MPPT control of the hydraulic wind turbine

4.2 液压型机组最优功率追踪控制仿真与实验结果分析

通过仿真模型和实验平台模拟风速典型工况，当风速由7m／s调整为8m／s时，仿真和实验结果如图16所示.当风速由8m／s调整为7m／s时，仿真和实验结果如图17所示.

图16 风速上升时仿真和实验结果Fig.16 Simulation and experimental results when wind speed rises

图17 风速下降时仿真和实验结果Fig.17 Simulation and experimental results when wind speed drops

由图16 可知，当风速由7 m／s调整为8 m／s时，系统的压力和发电功率逐渐增大，风力机完成最优功率追踪控制后压力稳定于14MPa，发电功率稳定于6.5kW，与图14（b）中模拟风力机8m／s风速下的最优功率相等.

由图17 可知，当风速由8 m／s调整为7 m／s时，系统的压力和发电功率逐渐减小，风力机完成最优功率追踪后压力稳定于12MPa，发电功率稳定于4.2kW，与图14（b）中模拟风力机7m／s风速下的最优功率相等.

仿真的实验结果表明，变步长最优功率追踪控制方法能够有效地实现最优功率追踪控制.

5 结 论

（1）建立了风力机特性数学模型和液压型机组主传动闭式系统数学模型.针对机组最优功率追踪问题，提出变步长的最优功率追踪控制方法，通过运行区间判断，调整给定功率大小，从而实现最优功率追踪控制.

（2）通过仿真和实验得出变步长最优功率追踪控制方法的动态响应参数，采用变步长最优功率追踪控制方法，系统压力和发电功率可准确地跟踪风速变化，对液压型机组最优功率追踪具有良好的控制效果.

［1］ International Energy Agency.Global carbon－dioxide emissions increase by 1.0 Gt in 2011to record high［Z／Ol］.http：／／www.iea.org／newsr－oomandevents／news／2012／may／name，27216，en.html.

［2］ 赵仁德，王永军，张加胜.直驱式永磁同步风力发电系统最大功率追踪控制［J］.中国电机工程学报，2009，29（27）：106－111.ZHAO Rende，WANG Yongjun，ZHANG Jiasheng.Maximum power point tracking control of the wind energy generation system with direct－driven permanent magnet synchronous generators［J］.Proceedings of the CSEE，2009，29（27）：106－111.

［3］ 孔祥东，艾超，王静.液压型风力发电机组主传动控制系统综述［J］.液压与气动，2013（1）：1－7.KONG Xiangdong，AI Chao，WANG Jing.A summary on the control system of hydrostalic drive train for wind turbines［J］.Chinese Hydraulics ＆Pneumatics，2013（1）：1－7.

［4］ HUI J.An adaptive control algorithm for maximum power point tracking for wind energy conversion systems［D］.Kingston，Jamaica：Queen＇s University，2008.

［5］ 童亦斌，刘展，刘远远.MW 级风电机组最大功率追踪复合控制策略［J］.农业机械学报，2011，42（9）：129－132.TONG Yibin，LIU Zhan，LIU Yuanyuan.Maximum power point tracking compound control strategy of MW level wind turbines［J］.Transactions of the Chinese Society for Agricultural Machinery，2011，42（9）：129－132.

［6］ 马卫东.风力发电机组最大功率追踪［J］.高压电器，2012，48（7）：57－65.MA Weidong.Maximum power point tracking for wind turbine［J］.High Voltage Apparatus，2012，48（7）：57－65.

［7］ 张勇，曲华龙.最大功率追踪与变速恒频风力发电［J］.电机与控制应用，2009，36（12）：26－29.ZHANG Yong，QU Hualong.Max－output tracing and wind turbine generator with variable－speed and constant frequency［J］.Electric Machines ＆Control Application，2009，36（12）：26－29.

［8］ 陈毅东.全功率变流器风机运行品质优化控制技术的研究［D］.秦皇岛：燕山大学，2012.

［9］ THONGAM J S，OUHROUCHE M.MPPT control methods in wind energy conversion systems［G］／／CARRIVEAU R.Fundamental and advanced topics in wind power.Rijeka，Croatia：In Tech，2011：339－360.

［10］ 韩利坤.基于能量液压传递的风力机“变速恒频”技术研究［D］.杭州：浙江大学，2012.

［11］ JIANG Zhenhua，YU Xunwei.Modeling and control of an integrated wind power generation and energy storage system［C］／／Power ＆Energy Society General Meeting of IEEE.Calgary，Canada：IEEE，2009：1－8.

［12］ 周云龙，杨承志，李律万.新型双风轮风力机气动特性的三维流场数值模拟［J］.动力工程学报，2012，32（9）：698－704.ZHOU Yunlong，YANG Chengzhi，LI Lüwan.3D flow field numerical simulation on aerodynamic characteristics of new double－rotor wind turbines［J］.Journal of Chinese Society Power Engineering，2012，32（9）：608－704.

［13］ 王金铭，卢奭瑄，何新，等.大型风力发电机风能利用系数参数拟合的研究［J］.太阳能学报，2012，33（2）：221－224.WANG Jinming，LU Shixuan，HE Xin，et al.Study on parameters matching of rotor power coefficient for large scale wind turbine［J］.Acta Energiae Solaris Sinica，2012，33（2）：221－224.

［14］ 张刚.液压型风力发电机组主传动系统功率控制研究［D］.秦皇岛：燕山大学，2012.