90°矩形截面弯头内置导流板的布置优化研究

于 飞， 刘 明， 李卫东， 严俊杰

（1.西安交通大学 动力工程多相流国家重点实验室，西安710049；2.华能国际电力股份有限公司，北京100031）

我国“十二五”规划纲要中提出：“十二五”期间，我国单位国内生产总值能源消耗降低16%；单位国内生产总值二氧化碳排放量降低17%；主要污染物排放总量显著减少，其中化学需氧量、二氧化硫排放量分别减少8%，氨氮、氮氧化物排放分别减少10%.火电厂是一次能源的消耗大户，因此提高火电厂的能源利用率、减少污染物的排放量对我国节能减排目标的实现意义重大.

随着节能减排工作的深入，烟风煤粉系统节能逐渐引起火电企业的重视.火电厂烟风煤粉管道是烟道、风道、原煤、制粉、送粉和其他有关管道的总称，用于输送烟气、冷风、热风、煤粉及原煤等介质［1］，其设计及运行情况不仅影响着引、送风机等通风设备的选型［2］，同时影响着锅炉烟风煤粉系统的能耗以及燃烧器、旋风分离器和除尘器等［3－5］与烟风煤粉管道相连接的设备的安全经济运行.作为火电厂烟风煤粉管道中最重要且常用的异形件形式之一，弯头具有局部阻力损失较大的特点.这主要是由于流体流过转弯处后，由于离心力与惯性力的共同作用，内壁流体不能再继续沿着壁面流动，从而容易在转弯后的内侧壁面附近形成局部涡流区，管道横截面上也会形成严重的二次流动，这些因素均使得流体经过缓转弯头后形成的流场均匀性较差.而气流转弯后速度场和压力场分布的紊乱也容易造成火电厂烟风煤粉管道振动和噪声超标现象［6］.因此，研究气流转弯时的流场控制具有重要意义.

在工程实际中，一般需要在弯头处添加导流板以起到均匀流场的作用.根据DL／T 5121—2000《火力发电厂烟风煤粉管道设计技术规程》［1］的规定：对于同心圆缓转弯头，当截面尺寸满足a／b≤1.3时宜装设导流板；a／b＜0.8时宜装设1～2片导流板，0.8≤a／b≤1.3时宜装设1片导流板；导流板中心角宜取为90°，且与弯头同圆心沿径向等间距布置（a，b 分别为转弯横截面的高度和宽度）.该规定主要是基于二维设计理念提出的，随着大容量、高参数机组的发展，烟风通道的尺寸越来越大，对烟风通道的结构形式要求也更加严格，该规定已经不能满足火电厂烟风煤粉管道设计优化的要求.

随着科学技术的发展，计算流体力学（CFD）技术已广泛应用于各工业领域.采用CFD 方法对烟风煤粉管道进行三维优化设计和数值模拟，可优化管内的三维流场、降低其阻力损失，同时优化与管道相连的各设备的运行状态，实现火电机组的高效安全运行.另外，与实验研究相比，CFD 方法在整体管道及其内部部件结构优化方面具有较大优势，主要表现在：可以方便地对研究对象的结构进行微调，并重新建模计算，计算速度快、灵活性和可操作性强，可以节省大量人力物力成本.因此，CFD 方法已被广泛用于火电厂烟风煤粉管道的设计和改造中［7－10］.

国内学者曾对工业应用很广的小尺寸方形截面缓转弯头加装导流板进行了基于气固两相流动的数值模拟研究［11］，得出了导流板的优化布置方案，但具有一定局限性，如几何尺度较小、未考虑转弯半径对结果的影响、未采用量化指标衡量考察流场均匀程度特性等.

笔者结合现行标准，运用大型商业软件Fluent，以空气作为流动介质，对缓转弯头内多种导流板布置方式进行了三维数值模拟，得到转弯后的流场分布，并通过对转弯后流场均匀性的量化计算，得出导流板的最优布置方式.

1 计算模型的建立

1.1 几何模型

缓转弯头的三维几何模型如图1所示，其中截面宽、高分别为b＝1.0m，a＝0.4m；考虑入口、出口直管段影响，采用入口直管段长L1＝3m，出口直管段长L2＝6m；采用与缓转弯同心的圆弧作为导流板，数量均为1片，由于导流板厚度（3～5mm）占总烟道尺寸的比例很小，所以在建模过程中忽略导流板厚度.

研究过程中，通过改变转弯半径与截面宽度之比R／b、导流板中心角θ、导流板起（止）角度α（β）、决定导流板分割流道方式的比值b1／b2，以获得最优的导流板布置方式.

图1 几何模型Fig.1 Geometric model of the 90degree elbow

1.2 湍流模型

考虑到流体流过缓转弯头后的流动比较复杂，存在旋流和严重的二次流，故采用Realizable k－ε 湍流模型，与标准k－ε 模型、RNG k－ε 模型相比，该模型具有保持雷诺应力与真实湍流一致的优点［12］，在旋流计算、带方向压强梯度的边界层计算和分离流计算等问题中，计算结果更符合真实情况，同时在带二次流的复杂流动计算中表现出色.

1.3 网格划分

用ICEM CFD 对几何模型进行网格划分，整个区域均采用结构化网格，并对壁面和导流板两侧表面附近网格进行局部加密（见图2）.

图2 网格局部加密Fig.2 Local mesh refinement

另外，配合湍流模型进行近壁处理所采用的标准壁面函数法要求壁面y＋的取值在一定的范围内（30～300）.对模型进行不同数量和不同壁面加密程度的网格划分，计算后得到的壁面y＋的范围见图3.因此选择网格数量为130万个左右、壁面第一层网格厚度为7.2mm 的网格划分方式，可以使数值模拟计算在具有一定可靠性的同时节省计算时间.而其后进行的网格无关性检验也证明，130万的网格已经足以精确模拟反映流场特性的各种参数.

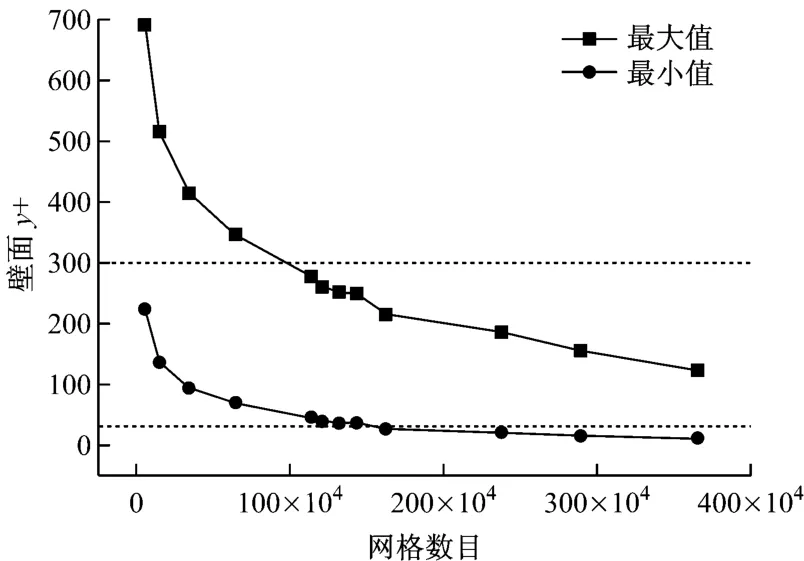
图3 不同网格数目下的壁面y＋Fig.3 Influence of mesh number on y－plus value of the wall

1.4 边界条件

模型采用速度入口边界条件，速度大小vin＝15 m／s；采用压力出口边界条件，表静压pout＝0Pa；定义弯管内表面、导流板两侧表面均为绝对粗糙度K＝0.4mm的固壁边界.

1.5 导流板布置性能评价方法

在弯头中布置导流板是为了控制流体转弯后局部涡流和截面二次流的形成，以提高流场均匀性，达到降低局部阻力损失的目的.因此，需对转弯后流场的均匀程度选择合适的量化指标进行衡量，并通过比较判断不同导流板布置方式的合理程度.

采用图1所示的几个参考截面处（Li＝2.0m）以及出口截面处的速度标准差Sv或总压标准差Sp作为衡量导流板对弯头后流场均流效果的量化指标，并结合流线图和压力云图进行分析研究.Sv和Sp的表达式如下：

式中：vi、pi分别为参考截面上各节点的速度和压力；分别为截面上各节点的平均速度和平均压力；n为截面上的节点数目.

2 计算结果与分析

现有标准规定，当矩形截面缓转弯头的高宽比a／b≤1.3时宜布置导流板，但并未指出导流板的转弯半径R 的范围.

分别对不同R／b 条件下无导流板模型以及加装1片中心角为90°、均分流道（b1＝b2）布置的导流板模型进行数值模拟.图4为加装导流板前后参考截面1处的Sp值.由图4可知，随着转弯半径的增大，加装导流板后的均流效果越来越不明显：当1.0≤R／b≤1.5时，Sp在加装导流板后下降10%～30%，而当1.5＜R／b＜2.0时，Sp下降小于10%.因此，在1.0≤R／b≤1.5 的缓转弯头中才有必要布置导流板.为此，着重研究1.0≤R／b≤1.5 范围内弯头导流板布置的优化.

图4 不同R／b的弯头模型加装导流板前后转弯后的Sp 值Fig.4 Spvalues in the section after turning point of the elbow with different R／bratios before and after addition of guide plate

2.1 导流板起止位置的影响

与急转弯头相比，缓转弯头的转弯半径大，按照现有国家标准规定的添加方式所耗费的钢材较多.从经济性角度考虑，要减少钢材消耗量最直接的方法就是减小导流板的中心角θ，因此需要研究导流板布置起止位置对均流效果的影响.

采用R／b＝1.0 的模型，导流板均分流道布置（b1＝b2），保持导流板中心角θ分别为60°、70°和80°不变，通过改变图1中α和β 的大小，改变导流板的起止位置，对比位于转弯后的3个参考截面及出口截面处的Sv值（见图5）.由图5可以看出，在导流板中心角θ＜90°的情况下，导流板靠后布置（β＝0°）的综合均流效果最好.

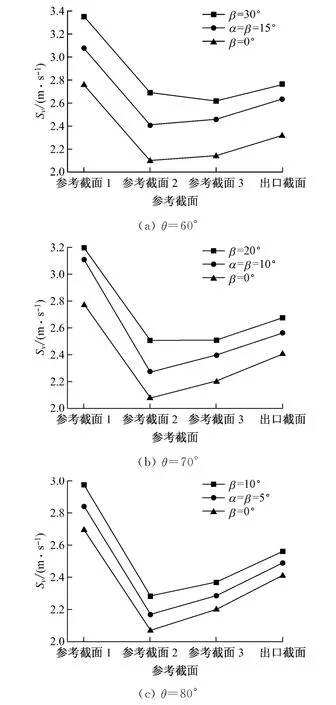
图5 不同导流板起止位置模型转弯后的Sv 值Fig.5 Svvalues of reference sections after turning point of the elbow with guide plate at different start／end positions

图6 为θ＝60°时，导流板靠前布置（α＝0°）、居中布置（α＝β＝15°）和靠后布置（β＝0°）的截面流线图.由图6可以看出，导流板内侧流体在转弯后期由于离心力和惯性的作用“甩”向弯管外侧，导流板靠后布置能更好地抑制这种运动；导流板靠后布置能够有效地减小转弯后内侧管壁死区漩涡的面积，因此能更好地均匀流场.

2.2 导流板中心角的影响

进一步研究靠后布置（β＝0°）时，导流板中心角θ对转弯后流场均匀性的影响，为了排除转弯半径对结果的影响，使结论可靠性更高，采用R／b 分别为1.0、1.25和1.5的模型进行计算.

图7给出了模型在不同转弯半径下转弯后的流场均匀性随θ的变化.由图7可以看出，R／b 越小，转弯越急，改变θ对转弯后流场均匀性的影响越明显；但当θ＞60°后，流场均匀性的变化均比较平缓.故采用θ＝60°的导流板代替技术规程中规定的θ＝90°的导流板，在节省钢材的同时可起到较好的均流效果.

图6 不同导流板起止位置模型的截面局部流线图Fig.6 Local section streamlines with addition of guide plate at different start／end positions

图7 不同转弯半径下导流板模型转弯后流场均匀性随θ的变化Fig.7 Influnce of flow field uniformity after turning point of the elbow with guide plate installed at different turning radii

2.3 导流板分割流道方式的影响

通过改变b1与b2的比值来改变导流板分割流道的方式，研究导流板分割流道方式对缓转弯后流场均匀性的影响.

首先研究导流板适宜靠近转弯外侧布置还是靠近转弯内侧布置.图8给出了b1／b2分别取0.5、1.0和2.0时，R／b＝1.0的缓转弯头转弯后各参考截面上的Sv值.通 过 对 比 可 以 看 出，当b1／b2＝0.5 时（即导流板靠近转弯内侧时），转弯后的流场较均匀.

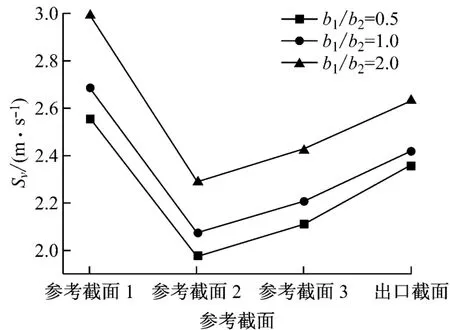
图8 导流板分割流道方式对转弯后流场均匀性的影响（1）Fig.8 Influence of channel partitioning way by guide plate on flow field uniformity after turning point of the elbow（1）

进一步针对导流板靠近转弯内侧布置的情况（b1／b2＜1.0）进行细化研究，以得到最佳的导流板分割流道方式.对R／b为1.0、1.25和1.5的模型，改变b1／b2取值分别为0.33、0.4、0.5、0.67和1.0，对比转弯后各参考截面处的流场均匀性（见图9）.由图9 可以看出，对于不同R／b 的缓转弯头模型，均满足当b1／b2＝0.4～0.5 时，转弯后各参考截面处的流场比较均匀.

3 导流板的优化布置方式

根据前文所述的导流板优化布置方式，对R／b＝1.5的缓转弯头内的导流板布置方式进行综合改造分析.

采用β＝0°、b1／b2＝0.5 的改进导流板添加方式，在不同θ下与现有国家标准规定的导流板均分流道方式（b1／b2＝1.0）进行对比.

图10给出了不同导流板布置方式模型转弯后的Sv值.由图10 可以看出，在θ 较小时，采 用b1／b2＝0.5的改进导流板分割流道方式的均流效果并没有b1／b2＝1.0（即均分流道方式）的均流效果好；但在θ＞60°之后，导流板的均流效果已经变得非常明显，并且改进分割流道方式所带来的更好的均流效果开始显现.

因此，采用θ＝60°～90°、靠后布置（β＝0°）、靠近转弯内侧布置（b1／b2＝0.4～0.5）的导流板具有最优的均流效果.

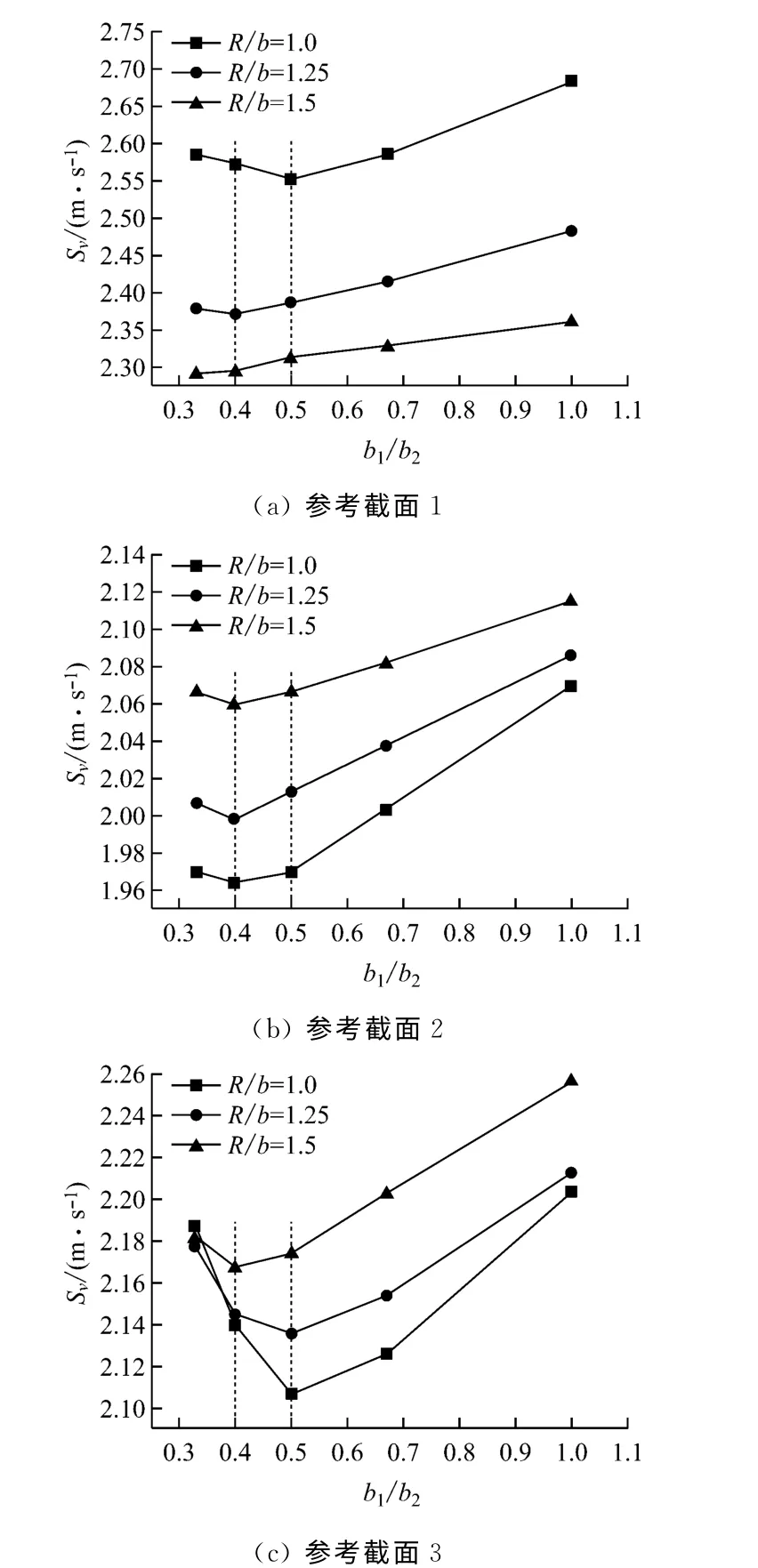
图9 导流板分割流道方式对转弯后流场均匀性的影响（2）Fig.9 Influence of channel partitioning way by guide plate on flow field uniformity after turning point of the elbow（2）

图10 不同导流板布置方式模型转弯后的Sv 值Fig.10 Sv values in the section after turning point of the elbow with guide plate in different arrangements

图11 给出了不同导流板布置方式模型的入口、出口总阻力损失.由图11 可以看出，按照上述θ＝60°、靠后布置（β＝0°）、不均分流道（b1／b2＝0.5）的最优导流板布置方式布置1片导流板的弯头模型，其入口、出口总阻力损失Δp 相比现有标准推荐的导流板布置方式有一定下降，再次证明该导流板布置方式的优越性.

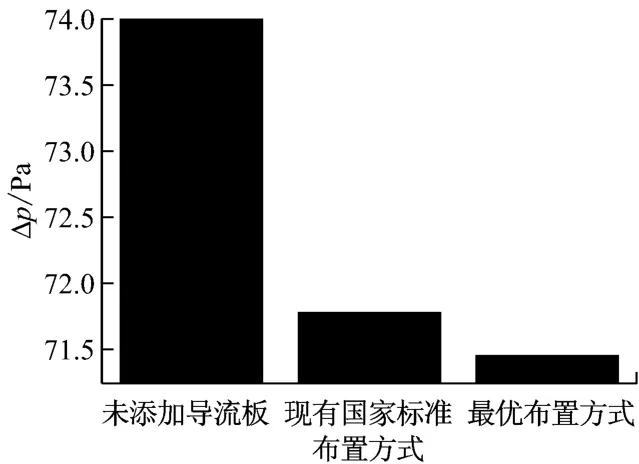
图11 不同导流板布置方式模型的入口、出口总阻力损失Fig.11 Total pressure loss of the elbow with guide plate in different arrangements

4 结 论

（1）随着R／b的增大，在转弯内部添加导流板的均流效果变差，当R／b≤1.5时，加装导流板对转弯后流场的均流作用较明显.

（2）导流板采用β＝0°的靠后布置方式能够更好地抑制导流板内侧流体向外运动，并能减小转弯后内侧管壁处的死区漩涡面积，均流效果较好.

（3）随着导流板中心角θ的增大，导流板中心角变化对转弯后流场均匀性的影响越来越小.对于1.0≤R／b≤1.5的缓转弯头，从节省钢材的角度出发，可不采用现有国家标准规定的θ＝90°，只需满足θ≥60°的条件即可.

（4）导流板接近转弯内壁面的分割流道方式（b1／b2＜1.0）可以更好地抑制流体与壁面的分离，使转弯后流场更加均匀.对于1.0≤R／b≤1.5的缓转弯头，满足b1／b2＝0.4～0.5的分割流道方式可以起到最好的均流作用.

［1］ 国家电力公司华东电力设计院.DL／T 5121—2000火力发电厂烟风煤粉管道设计技术规程［S］.北京：中国电力出版社，2001.

［2］ 车得福，庄正宁，李军，等.锅炉［M］.2版.西安：西安交通大学出版社，2008：567－568.

［3］ 潘卫国，林泉，孙坚荣，等.一次风喷口速度分布对四角切圆燃烧锅炉炉内空气动力场影响的数值研究［J］.动力工程，2004，24（4）：495－500.PAN Weiguo，LIN Quan，SUN Jianrong，et al.Numerical research on the effect of velocity difference between left and right parts of primary air nozzle in the dynamic field for a tangential firing boiler［J］.Power Engineering，2004，24（4）：495－500.

［4］ 李战国，刘志成，贺军，等.旋风分离器的入口烟道布置对性能的影响［J］.中国电机工程学报，2009，29（17）：1－7.LI Zhanguo，LIU Zhicheng，HE Jun，et al.Influence of inlet duct layouts on cyclone performance［J］.Proceedings of the CSEE，2009，29（17）：1－7.

［5］ 仇中柱，潘卫国，李芃，等.数值模拟与模化在电除尘器改造中的应用［J］.华东电力，2010，38（6）：927－930.QIU Zhongzhu，PAN Weiguo，LI Peng，et al.Application of numerical simulation and modeling in retrofit of electrostatic precipitator［J］.East China Electric Power，2010，38（6）：927－930.

［6］ 韩卫东.烟风道内支撑优化设计［J］.机电信息，2011（15）：174－175.HAN Weidong.Optimization design of smoke duct support［J］.Mechanical and Electrical Information，2011（15）：174－175.

［7］ 陶克轩，常毅君，张波，等.电厂除尘器入口烟道数值模拟及改造［J］.热力发电，2011，40（1）：52－54.TAO Kexuan，CHANG Yijun，ZHANG Bo，et al.Numerical simulation and retrofit of inlet flue duct for eletrostatic precipitator［J］.Thermal Power Generation，2011，40（1）：52－54.

［8］ 康振兴，邵杰，李国堂.引风机后汇流烟道的数值模拟［J］.电力建设，2012，33（4）：58－60.KANG Zhenxing，SHAO Jie，LI Guotang.Numerical simulation of conflux flue behind induced draft fan［J］.Electric Power Construction，2012，33（4）：58－60.

［9］ 刘明，孟桂祥，严俊杰，等.火电厂除尘器前烟道流场性能诊断与优化［J］.中国电机工程学报，2013，33（11）：1－6.LIU Ming，MENG Guixiang，YAN Junjie，et al.Flow characteristics diagnosis and optimization for dust collectors inflow duct in thermal power plants［J］.Proceedings of the CSEE，2013，33（11）：1－6.

［10］ 齐晓娟，王万林，李凤瑞.火电厂脱硫后烟道内气流分布改进的CFD 模拟［J］.华东电力，2013，41（1）：220－223.QI Xiaojuan，WANG Wanlin，LI Fengrui.Alteration of flue gas distribution in the gas duct in the back of desulphurization with CFD computation software［J］.East China Electric Power，2013，41（1）：220－223.

［11］ 谢振华，周艳荣.90°方截面弯管内加装导流板的优化研究［J］.应用基础与工程科学学报，2009，17（4）：566－572.XIE Zhenhua，ZHOU Yanrong.Optimization research on guide plate installed in quadrate 90°curved duct［J］.Journal of Basic Science and Engineering，2009，17（4）：566－572.

［12］ 于勇，张俊明，姜连田.FLUENT 入门与进阶教程［M］.北京：北京理工大学出版社，2008：23－24.