Convolutions,Tensor Products and Multipliers of the Orlicz-Lorentz Spaces∗
Hongliang LI Jiecheng CHEN
1 Introduction
The convolution operator has been studied for many years.The classical type,called Young inequality,Lp∗LqLr(1 LetAbe a Banach algebra.By a left(right)BanachA-module we mean(see[8])a Banach spaceV,which is a left(right)A-module in the algebraic sense,and for which wherekis a constant independent ofa,v. IfVandWare left(right)BanachA-modules,then HomA(V,W)will denote the Banach space of all continuousA-module homomorphisms fromVtoWwith the operator norm.HomA(V,W),as a rule,is called the space of multipliers fromVtoW. The definition of the tensor product of Banach modules can be found in[8–9].LetAbe a Banach algebra,andVandWbe left and right BanachA-modules respectively.Suppose thatV⊗γWdenotes the projective tensor product(see[10])ofVandWas Banach spaces(γis the greatest crossnorm in[11],[12,p.36]).LetKbe the closed linear subspace ofV⊗γWwhich is spanned by all the elements of the form Now the quotient Banach spaceVW/Kis called theA-module tensor productVW. The following isomorphism was proved by Rieffel[8],where the notationW∗is the dual ofW.The linear functional on HomA(V,W∗),which corresponds tot=W,has value atT∈HomA(V,W∗).The topology on HomA(V,W∗)defined by the linear functional of this form corresponds to the weak∗-topology(VW)∗,which is called ultraweak∗-operators topology(see[9,13]). In this paper,we get the concrete representation of the tensor products of the Orlicz-Lorentz spacesand obtain the multipliers of the Orlicz-Lorentz spaces by(1.1).For more details about tensor products and multipliers,one can also refer to[14–18]and so on. LetM(G,µ)be the class of all measurable and almost everywhere finite functions on(G,µ).Forf∈M(G,µ),a non-increasing rearrangement off,is a non-increasing functionf∗on R+≡(0,+∞)which is equimeasurable with|f|.The rearrangementf∗is defined by the equality(see[19]) where We sayφ:[0,∞)→[0,∞)is a Young function ifφis non-decreasing and convex withφ(0)=0,andφ(x)=∞.The Young conjugateφ∗of the Young functionφis defined by The Orlicz-Lorentz spaces(G)(see[20–21])associated to the Young functionφand a weightwon R+(nonnegative locally integrable functions in R+),are the set off∈M(G,µ)such that for someλ>0,we have(λf)<∞,where (we assume that the weightwvanishes in[µ(G),∞)).Let If there is no ambiguity,we indicate=Ifw(t)=1,then=is an Orlicz space(see[22–23]);ifφ(t)=(1≤p<∞),then=(w)is a Lorentz space(see[24–25]).Additionally,let called the subspace of finite elements ofIf groupGis discrete,the notationsandare used instead ofand Given an arbitrary functionD:[0,∞)→[0,∞),we say thatDsatisfies condition∆2in symbolG∈∆2when A Young functionFis said to satisfy∆′condition in symbolF∈∆′if there existsC>0 such that Clearly ifF∈∆′,thenF∈∆2.By[26,Thm.3.1],we know that ifµ(G)=∞,W∈∆2,W(∞)=∞orµ(G)<∞,then There are many papers devoted to researching Hardy-type inequalities on monotone functions.Letfbe a nonnegative function on R+,the Hardy operator be andf↓indicate thatfis a nonnegative nonincreasing function in R+.In[27,Thm.2.3],the author got that ifφ∈∆′,then if and only if there is a constantH>0 such that Obviously,(2.2)implies thatcan be normable ifφ∈∆′.Ifφ=,then(2.3)implies thatw∈(see[28–29]).Ifw,φsatisfy the inequality(2.2),we sayw∈,and let As usual,f≈gindicates the existence of a universal constantB>0(independent of all parameters involved)so thatf≤g≤Bf.In the sequel,Cdenotes a positive constant which need not be the same at different occurrences.Ifwis a weight on R+,we denoteW(t)=w(s)ds. In the rest of this paper,Gwill be a unimodular locally compact abelian group,with Haar measureµ.Letφbe a Young function.A generalized inverse function:[0,∞]→[0,∞]is defined as It is said in[3]that(i=1,2,3)satisfy condition(+)for l.a.(s.a.)[a.a]if there existk>0,δ>0,such that whenφ1(u)≥δ,φ2(v)≥δ(φ1(u)≤δandφ2(v)≤δ)[u,v≥0].It is said that(i=1,2,3)satisfy condition(++)for l.a.(s.a.)[a.a],if for everyα>0,there existk>0,δ>0,such that whenφ1(u)≥δ,φ2(v)≥δ(φ1(u)≤δandφ2(v)≤δ)[u,v≥0].[3,Prop.2]showed that condition(+)for l.a.(s.a.)[a.a]is equivalent to the following one:There existl,δ>0,such that ifu≥δ(u≤δ)[u≥0]. SinceGis a unimodular locally compact group,by virtue of the definition of convolution(see[1]),Hewitt and Ross[4,Ch.5,Sec.20]indicated that the operator satisfies that So suchTis a convolution operator.Thus by[1], Lemma 3.1Let w∈(i=1,2)andw≥1.Suppose that φi(i=1,2,3)satisfy condition(+)for a.a.and≤where k is the constant from(+),so then(λf∗g)≤1. ProofBy(3.1)we have Since(i=1,2,3)satisfy condition(+)for a.a.andw(s)≥1,s>0,the right hand of the last inequality Since by Jensen’s inequality and≤t,t>0,we get that the right part of(3.2) Remark 3.1Ifw≥1 is replaced byw≥c(c>0 is a nonnegative constant)in the preceding lemma,then the result also holds. The next theorems give sufficient conditions for embedding of the spaces Theorem 3.1(I)Let G be nondiscrete,w∈(i=1,2),w≥c(c>0be a nonnegative constant)and(i=1,2,3)satisfy condition(+)for l.a.if G is compact and(+)for a.a.if G is noncompact.ThenIf additionallyis finite,then (II)Let G be discrete,w∈(i=1,2),and satisfy(+)for s.a.Then Proof(I)By[3]it is sufficient to prove only inclusion.Let firstGbe noncompact and(+)for a.a.Takef∈andg∈satisfying max((f),(g))Then applying Lemma 3.1 withλ=,we obtain≤1,which means by[3,Thm.1.2]thatf∗g∈andIfGis compact and(i=1,2,3)satisfy condition(+)for l.a.,then by[3,Lem.5]there exist functions(i=1,2,3)satisfying(+)for a.a.and equivalent tofor l.a.,which implies thatThus,the embedding follows in the same way as the above. To prove the inclusiontakef∈Let max((f),(g))≤minFor anyβ>0,supposeλ=2β.Then by(3.1)it follows that Sincew∈andf∈ Thus we can choose>0 such thatw(t)dt≤1.Then the right side of(3.3) Sincef∈there exists a constant>0,such that Thus Now we get But since each function in Λφ(w)is locally integrable,we get<∞,and thus On the other hand,in view of the condition(+),(3.5),and Jensen’s inequality,we also know Now,we see that the right hand of(3.4)is less than in fi nity,which completes the proof. (II)For this case,using[3,Lem.5],we can assume condition(+)for a.a.,and get the corresponding embedding by the same arguments as in(I). Theorem 3.2Let G be nondiscrete andsatisfy condition(++)for l.a.if G is compact and(++)for a.a.if G is noncompact.Let w∈,i=1,2and W(t)≥C1t,∀0 ProofSuppose thatGis compact.Takef∈such thatLetG1=whereδis from the condition(++)anda=min(µ(G1),µ(G2)).Letλ>0.Then First check I2and I3. Analogously,I3<∞.On the other hand,ifa=0,then I1=0;ifa0,then But≤so Thus J2<∞,likewise J3<∞. On the other hand,due to by the condition(++)we obtain whereKis from the condition(++)forα=12λ.SinceW(t)≥C1t,t∈[0,µ(G)],by Hardy lemma(see[19])we get which ends the proof. Lemma 3.2Let W∈∆2.Then (i)if w∈L1(G),S is dense inwhere S is the set of the simple functions in G; (ii)if wL1(G),is dense inwhere S0is the subset of S with support in a set of fi nite measures. ProofSimilar to Theorem 2.3.11 and Theorem 2.3.12 of[30]. From now on,let the weightwinsatisfyW∈ Let(x)=f(x−s).Then we have the following result. Proposition 3.1If φ is finite,then for every f∈the mapping s→fsof G intois continuous. ProofBy Lemma 3.2,it is sufficient to show that for any simple functionf,s→fsis continuous.Letf=and thenNow where△denotes the symmetric difference of sets.Then the following relation derives the result. Proposition 3.2Let φ,be two Young functions and>0.Let w be a weight onR+which satisfies W(t)≥Ct,C>0,w∈Bφ,w∈Then there is an approximate identity{}insuch that=1and f∗→f for every f∈ ProofLet{}be a decreasing neighborhood system at the origin inG.For eachα,there exists a non-negative continuous functionaαwith support insuch that=1.Thus by the Hardy lemma(see[19]),the conditionsW(t)≥Ctand>0,we get∈L1(G)and≤C.Letf∈Then by the condition>0 again and Theorem 3.1,we getand This shows by Proposition 3.1 that where the limit is taken over the net ofα. In this section,we letGbe a locally compact unimodular group(unless otherwise indicated).Set(x)=f().If for two Young functions(i=1,2)and a weightwon R+there exists a Young functionwhich makes(i=1,2,3)satisfy condition(+)for l.a.,ifGis compact and(+)for a.a.,ifGis noncompact,w∈(i=1,2),andw≥c(c>0 is a nonnegative constant),then in view of Theorem 3.1 we may define the bounded bilinear mapdas which lifts to a linear map naturally,D,fromIn addition,lettingw∈and>0,by Theorem 3.1 again,we can get thatcan be looked as right-modules. Definition 4.1The range of D,with the quotient norm,will be denoted by(w). According to the definition ofV⊗γW,consists of exactly those functionsh,onGat least one expansion of the formh=wheref∈g∈and and for anyh∈(w),the norm ofhis It can be seen that(w)is a Banach space of functions. LetKbe the closed linear subspace ofspanned by all elements of the form(h∗f)⊗g−f⊗(∗g),wheref∈andh∈Then the-module tensor productis the quotient space/K. In the next,we need the following conditions for weightwon R+and Young functionsφ1,φ2, (i)w≥c(c>0 is a nonnegative constant). (ii)w∈(i=1,2). (iii)w∈and>0. (iv)There exists a Young functionφ3which makesφi(i=1,2,3)satisfy condition(+)for l.a.,ifGis compact and(+)for a.a.,ifGis noncompact. (v)w∈and Remark 4.1By[6],if and=convex closure ofE2,thenfirst quadrant can deduce(iv). Theorem 4.1Let G be compact,weight w be nonincreasing and Young functions,,satisfy(i)–(iv).Thenis isomorphic to the space ProofIt suffices to show that the kernel ofDis exactlyK.Since (dis-balanced),the kernel ofDcontainsK. On the contrary,suppose thattis an element of the kernel ofD.Then and where the summation converges inbe an approximate identity ofsatisfying the condition in Proposition 3.2.For eachn,definetn∈by Then,from Proposition 3.2,∗converges tofor eachi,and by this one can prove thattnconverges totinNow givenn,s,andϵ>0,choosem0such that Choosem1>m0so that We observe that the second term on the right side of the following equality is inKand can be written by the definition of the cross norm.Letφ(y)=−x)].Sinceµ(G)<∞,1∈similar to proving the theorem of And[31,Thm.4,6,Thm.2.3],we easily get Thus Then the distance fromtntoKis less thanfor everyϵ>0,and sotn∈K.ForKis closed,t∈K. Lemma 4.1Suppose that weight w is onR+and Young functionsatisfy(i)–(iii)and(v).Let φ∈Cc(G)and define Tφf=f∗φ for f∈Then ProofIt is obvious thatφ∈withψa Young function.By[26],sincew≥c(c>0 is a nonnegative constant),there holds whereS(f)=In view of>0 and a simple fact that the functionis increasing,there exists a Young functionφsuch that i.e.,φ1,φ,satisfy(+)a.a.So by Theorem 3.1 and(4.1),it follows that iff∈then andTφis a bounded linear operator fromOn the other hand, for allf∈which ends the proof. The above lemma induces the following concept. Definition 4.2A locally compact unimodular group G is said to satisfy the propertyif every element ofcan be approximated in the ultraweak∗-operator topology by operators Theorem 4.2Let G be a locally compact unimodular group,w be a weight onR+and Young functionssatisfy(i)–(v).Then the following statements are equivalent: (A)G satisfies the property (B)The kernel of D is K such that ProofSuppose thatGsatisfies the propertySinceK⊂KerD,to show that KerD=K,it is enough to show that KerD⊂K.In other words,it suffices to show that by the Banach theorem,any bounded linear functional onwhich annihilatesKalso annihilates KerD.By(1.1),we know It can be seen from this that ifFis a linear functional that annihilatesK,there is an operatorT∈corresponding toF,such that for allt∈with expansion Suppose thatt∈KerDand has the form(4.4).Then the summation converging in the norm ofWe will show that⟨t,F⟩=0,or equivalently,by(4.3), SinceGis assumed to satisfy the property(w),there is a net{:j∈I}of(G)such that the operatorsconverge toTin the ultraweak∗-operator topology.Thus So,to check(4.5),it is enough to show that Sincewe deduce that This implies that Suppose conversely that KerD=K.To show that the operators of the formare dense in in the ultraweak∗-operator topology,we only need to show that the corresponding functionals are dense inin the weak∗-topology.Furthermore,it is sufficient to show that if these functionals,sayN,are viewed as functionals onthen their annihilatorsN⊥=K.Since and (see[32]),we haveN⊂.SoK⊂.Due to the assumption that KerD=K,we only need to prove that⊂KerD. Now,lett∈.Then=0 for allF∈Nand there existso that For anyF∈N,there is an operator∈corresponding toFsuch that It follows that that is,N⊥⊂KerD.This proves the theorem. Then by(4.1)–(4.2),we have the following result. Corollary 4.1Let G be a locally compact unimodular group,w be a weight onR+,Young functions φ1,φ2,satisfy(i)–(v),and G satisfy the property In the following,we illustrate the convolutions,tensor products,multipliers of Orlicz-Lorentz spacesLet 0 and the modular space as which induces Additionally,let=whereφ0=φq,w0= The next theorem needs a certain generalized Hardy-type inequality(see[33]).In[33,Thm.1.7],Bloom and Kerman give the sufficient and necessary condition of establishing the weighted integral inequality: whereφ1,φ2areN-functions(anN-functionφis a continuous Young function such thatφ(x)=0 if and only ifx=0 and=+∞)andTis a generalized Hardy operator.We need the special form of the above inequality: which holds if and only if there exists a positive constantDsuch that Whenφ(t)=t,(4.7)is a classical Hardy inequality(see[19])and it is obvious that(4.8)always holds. Now we have the following theorem. Theorem 4.3Let G be a unimodular locally compact group,T be a convolution operator k=T(f,g)=f∗g.Suppose that the following conditions hold:(a1)>1;(w≥c1>0,where c1is a constant;()φ(t)≤,whereis a constant,φ∈()are N-functions.Then there exists a constant C such that where=m and s≥1is a number such thatand the inequality(4.8)holds.In particular,if f∈then k∈ ProofSince(see[1–2]) we get For convenience,let=h.Then And by(4.8)it follows that the right part of the last inequality Now lettingy=and noticingw(t)≥c>0,φ∈∆′andφ(t)≤Ct,we have By Hlder inequality,it is easy to get that On the other hand,we can get that(one can take the same method which is used for the proof of(see[30])).Now the lemma is proved. Remark 4.2In view of the above theorem,we obtain ifφ,w,p1,p2,q1,q2,r,ssatisfy the conditions in the above theorem.At the same time,if there exists a constantC0>0 such that for any 0 and-module.Especially,ifφ(t)=t,w(t)=1,1≤<∞,1<<∞(obviously they satisfy the preceding conditions),then(4.9)is Additionally,using(4.9)and the same method in Theorem 4.1,Theorem 4.3 and Corollary 4.1,we can get the representations of the tensor products and multipliers onwhich contain the result of[13]. [1]O’Neil,R.,Convolution operators andL(p,q)spaces,Duke Math.J.,30,1963,129–142. [2]Yap,L.Y.H.,Some remarks on convolution operators andL(p,q)spaces,Duke Math.J.,36,1969,647–658. [3]Kamiska,A.and Musielak,J.,On convolution operator in Orlicz spaces.Congress on Functional Analysis,Madrid,1988,Rev.Mat.Univ.Complut.Madrid,2,1989,157–178. [4]Hewitt,E.and Ross,K.A.,Abstract Harmonic Analysis,Vol.I,Springer-Verlag,Berlin,1963. [5]Hudzik,H.,Kamiska,A.and Musielak,J.,On Some Banach Algebras Given by a Modular,A.Haar memorial conference,Vol.I,II,Budapest,1985,445–463,Colloq.Math.Soc.Jnos Bolyai,49,North-Holland,Amsterdam,1987. [6]O’Neil,R.,Fractional integration in Orlicz spaces,I.,Trans.Amer.Math.Soc.,115,1965,300–328. [7]Zelazko,W.,On the algebrasLpof locally compact groups,Colloq.Math.,8,1961,115–120. [8]Rieffel,M.A.,Induced Banach representations of Banach algebras and locally compact groups,J.Functional Analysis,1,1967,443–491. [9]Rieffel,M.A.,Multipliers and tensor products ofLp-spaces of locally compact groups,Studia Math.,33,1969,71–82. [10]Grothendieck,A.,Produits tensoriels topologiques et espaces nuclaires,Mem.Amer.Math.Soc.,16(16),1955,140 pp. [11]Bonsall,F.F.and Duncan,J.,Complete Normed Algebras,Ergebnisse der Mathematik und ihrer Grenzgebiete,Band 80,Springer-Verlag,New York-Heidelberg,1973. [12]Schatten,R.,A Theory of Cross-Spaces,Annals of Mathematics Studies,26,Princeton University Press,Princeton,N.J.,1950. [13]Avci,H.and Grkanli,A.T.,Multipliers and tensor products ofL(p,q)Lorentz spaces,Acta Math.Sci.Ser.B Engl.Ed.,27,2007,107–116. [14]Kerlin,J.E.,Representations of generalized multipliers ofLp-spaces of locally compact groups,Bull.Amer.Math.Soc.,79,1973,1223–1228. [15]Candeal Haro,J.C.and Lai,H.C.,Multipliers in vector-valued function spaces under convolution,Acta Math.Hungar.,67(3),1995,175–192. [16]ztop,S.,Multipliers of Banach valued weighted function spaces,Int.J.Math.Math.Sci.,24(8),2000,511–517. [17]zto,S.and Grkanli,A.T.,Multipliers and tensor products of weightedLp-spaces,Acta Math.Sci.Ser.B Engl.Ed.,21(1),2001,41–49. [18]Sair,B.,Multipliers and tensor products of vector valuedLp(G,A)spaces,Taiwanese J.Math.,7(3),2003,493–501. [19]Bennett,C.and Sharpley,R.,Interpolation of operators,Pure and Applied Mathematics,129,Academic Press,Inc.,Boston,MA,1988,xiv+469 pp. [20]Masty lo,M.,Interpolation of linear operators in Caldern-Lozanovskspaces,Comment.Math.Prace Mat.,26(2),1986,247–256. [21]Maligranda,L.,Indices and interpolation,Dissert.Math.,234,1984,1–49. [22]Orlicz,W.,ber eine gewisse Klasse von Räumen vom Typus B,Bull,Intern.Acad.Pol.,8,1932,207–220. [23]Luxemburg,W.A.J.,Banach function spaces,Thesis,Delft Technical Univ.,Delft,1955. [24]Lorentz,G.G.,Some new functional spaces,Ann.of Math.,51,1950,37–55. [25]Lorentz,G.G.,On the theory of spaces Λ,Pacific J.Math.,1,1951,411–429. [26]Kamiska,A.and Masty lo,M.,Abstract duality Sawyer formula and its applications,Monatsh.Math.,151(3),2007,223–245. [27]Li,H.L.,Hardy-type inequalities on strong and weak Orlicz-Lorentz spaces,Sci.China Math.,55(12),2012,2493–2505. [28]Aro,M.A.and Muckenhoupt,B.,Maximal functions on classical Lorentz spaces and Hardy’s inequality with weights for nonincreasing functions,Trans.Amer.Math.Soc.,320,1990,727–735. [29]Sawyer,E.,Boundedness of classical operators on classical Lorentz spaces,Studia Math.,96,1990,145–158. [30]Carro,M.J.,Raposo,J.A.and Soria,J.,Recent developements in the theory of Lorentz spaces and weighted inequalities,Mem.Amer.Math.Soc.,187,Amer.Math.Soc.,Providence,RI,2007. [31]An,T.,On products of Orlicz spaces,Math.Ann.,140,1960,174–186. [32]Conway,J.B.,A Course in Functional Analysis,Springer-Verlag,New York,1985. [33]Bloom,S.and Kerman,R.,WeightedLφintegral inequalities for operators of Hardy type,Studia Math.,110(1),1994,35–52.



2 Preliminaries for Orlicz-Lorentz Spaces










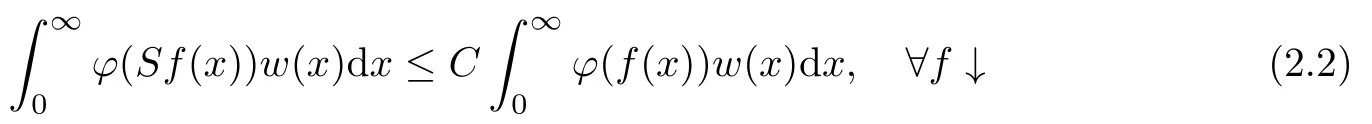
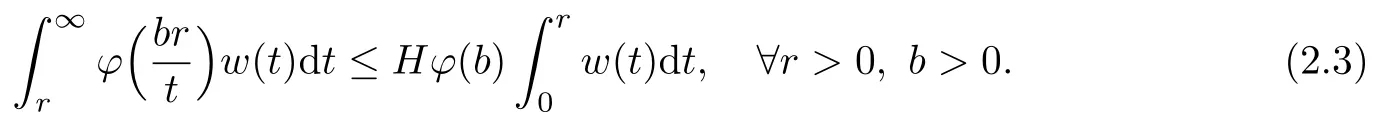

3 Convolutions of Orlicz-Lorentz Spaces
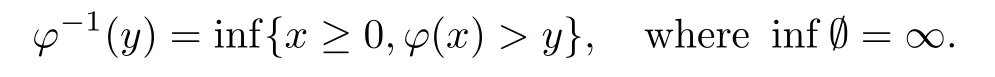



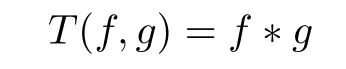




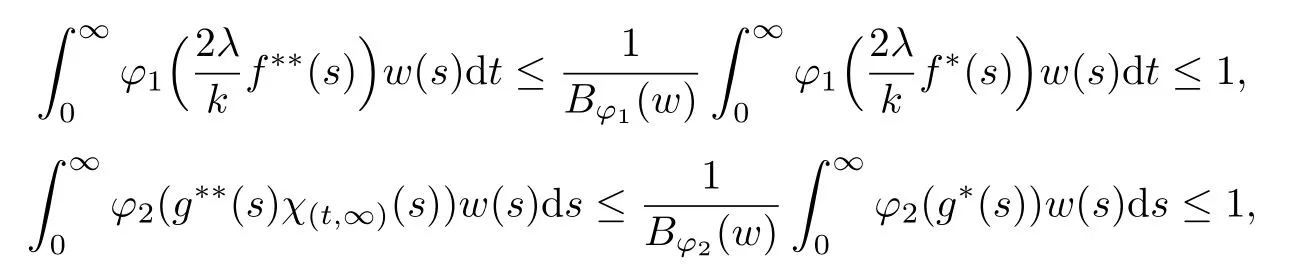
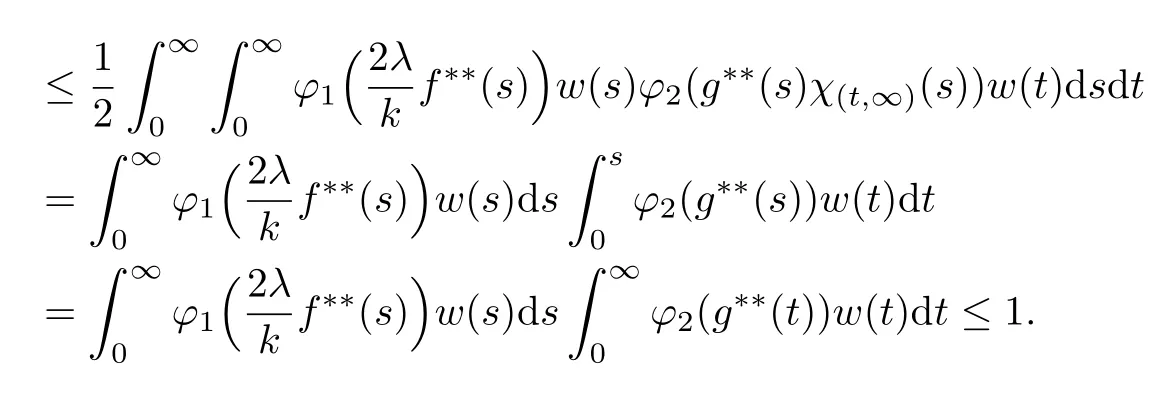


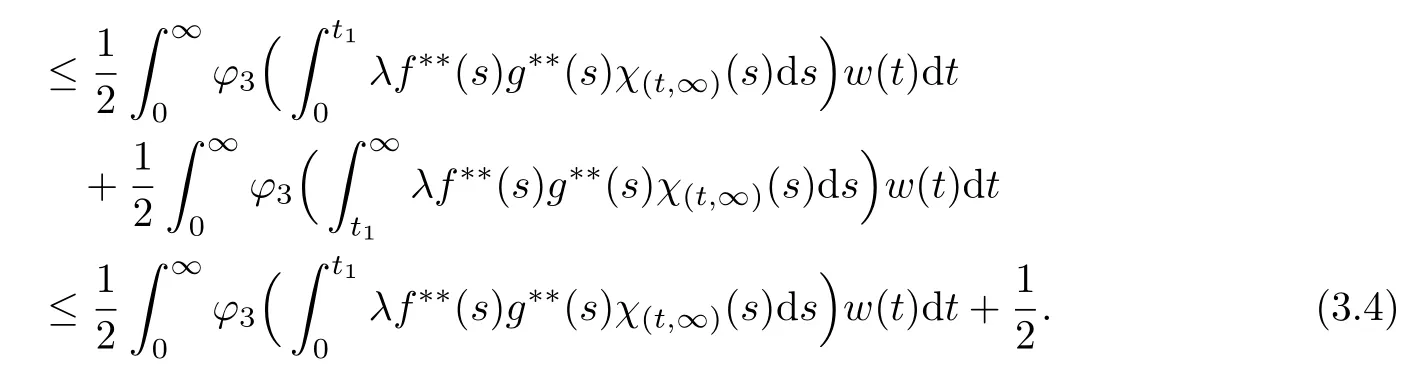

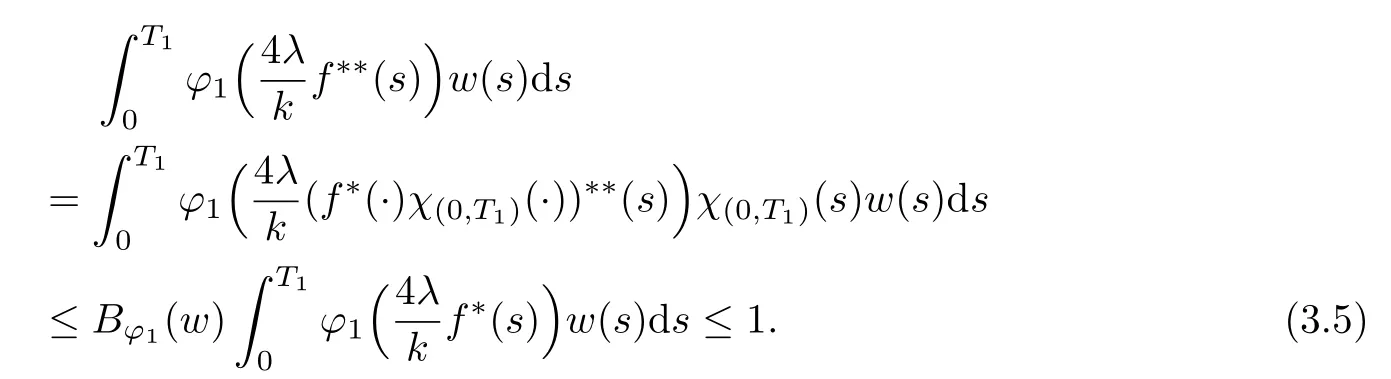













4 Tensor Products and Multipliers on Orlicz-Lorentz Spaces



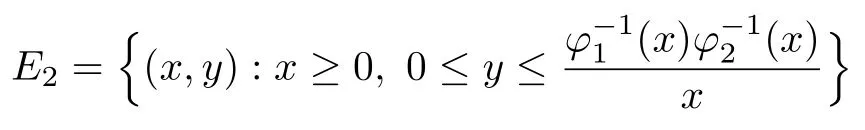






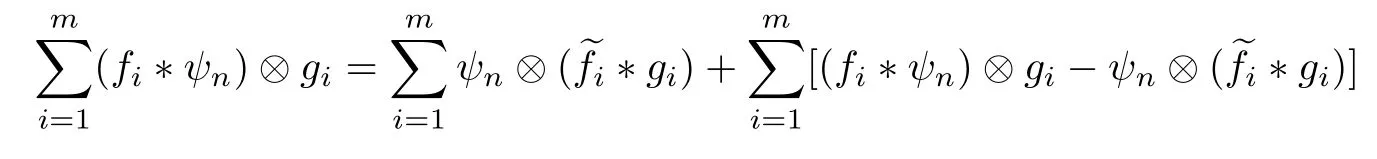
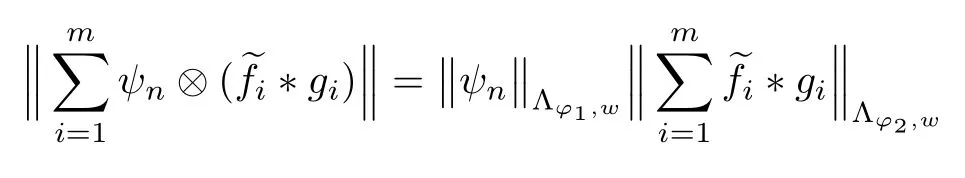


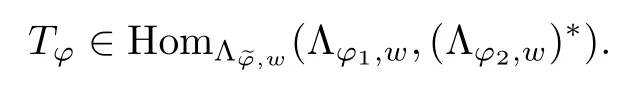












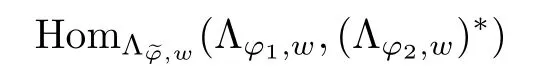
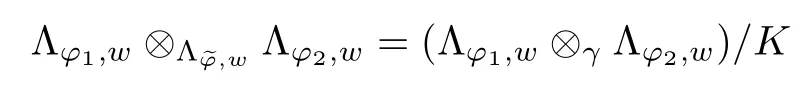


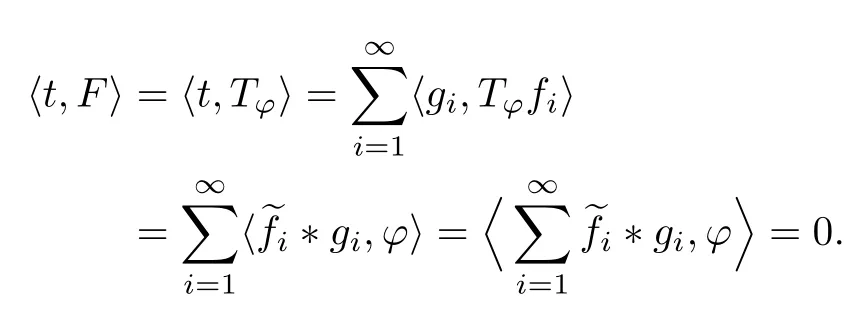


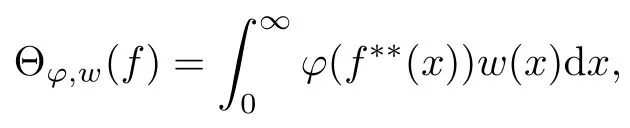




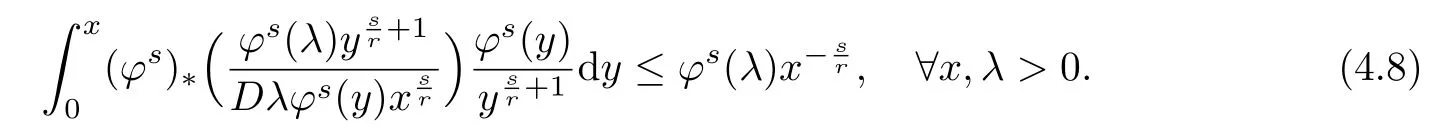


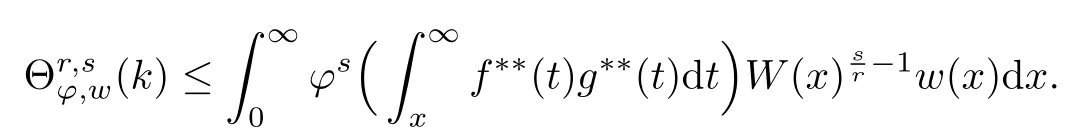








 Chinese Annals of Mathematics,Series B2015年3期
Chinese Annals of Mathematics,Series B2015年3期
