A Relation in the Stable Homotopy Groups of Spheres∗
Jianxia BAI Jianguo HONG
1 Introduction
Letpbe an odd prime andq=2p−2.It is well-known that the Adams-Novikov spectral sequence(ANSS)based on the Brown-Peterson spectrum is one of the most powerful tools to compute thep-component of stable homotopy groups of spheresS0,and theE2-term of the ANSS is(BP∗,BP∗)(see[1,7,10–11,15]).Moreover,we have the Adams spectral sequence(ASS)(see[1–2])based on the Eilenberg-MacLane spectrumKZ/p.
From[10–11],(BP∗,BP∗)=H1BP∗is generated byforn0,ps1,wherehas order.(B,BP∗)=BP∗is a direct sum of cyclic groups generated byforn0,ps1,j1,i0 and is subject to
wherea0=1,ak=−1 fork1.has order(see[10,14–15]).There is only partial information for(BP∗,BP∗)=H3BP∗which contains theporder generatorsγs,s1.
In 1985,D.C.Ravenel[13]first introduced the method of infinite descent and later used it to compute the first thousand stems of the stable homotopy groups of spheres at the prime 5.This method is devoted to computing the Adams-NovikovE2-term for a spheral spectrumS0by the following spectral sequence referred to as the small descent spectral sequence(SDSS)
anddr:
The following relation about the Toda bracket is showed by Ravenel in the topological SDSS(see[14,Proposition 7.5.11]or[15,Proposition 7.6.11]).Ifxis an element in stable homotopy groups of spheres and satisfiespx=0,=0 andα1x0,then
In this paper,we show that the condition⟩=0 holds for the elementx=withp7 by using the cobar complex ofBP-homology of the Smith-Toda spectrumV(2).Therefore,it follows that the relation
holds forp7.Applying this relation,we can prove thatis trivial inπ∗(S0)for 2sp−2,p7,butare not trivial inπ∗(S0)for 3sp−2,p7.
It is also proved thatis nontrivial inπ∗(S0),and we can further conjecture thatis nontrivial inπ∗(S0)forp7,2sp−2.
Letxandybe two elements in(BP∗,BP∗)and be permanent cycles.It is known that ifxy=0,then the homotopy product could still be nontrivial and represents an element in a higher Ext group.andγ3are two such elements.We know thatandγ3are permanent cycles and=0∈(BP∗,BP∗),butis nontrivial inπ∗and represents the elementfrom the relation(1.1).
The rest of this paper is organized as follows.In Section 2,the(topological)small descent spectral sequence will be introduced.In Section 3,we prove thatis nontrivial inπ∗(S0)by applying the May spectral sequence(MSS)and the small descent spectral sequence(SDSS).In Section 4,we recall the cobar complex and use it to calculate theE2-term of the Adams-Novikov spectral sequence forV(2).We show that the Toda bracket⟩is well defined.As a result,holds forp7 andbecause
2 The Small Descent Spectral Sequence
In this section,we recall the construction of the small descent spectral sequence.Ravenel computed theE1-term of this spectral sequence and used it to determine the stable homotopy groups of spheres in a certain range,see[14–16]for more details.
LetT(n)be the Ranevel spectrum(see[15])characterized by
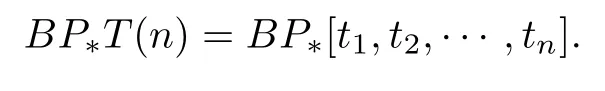
Then we have the following diagram:

whereS0denotes the sphere spectrum localized at an odd primep.Letdenote theq(p−1)andq(p−2)skeletons ofT(1)respectively.They are denoted byYandfor simplicity.Then

TheBP-homologies of them are
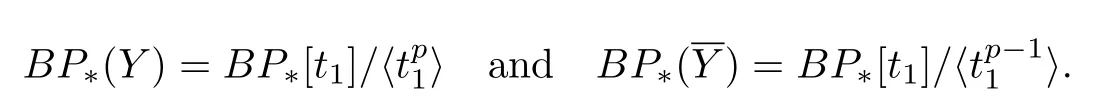
From the definition above,we get the following cofibre sequences:

and the short exact sequences ofBP∗homology
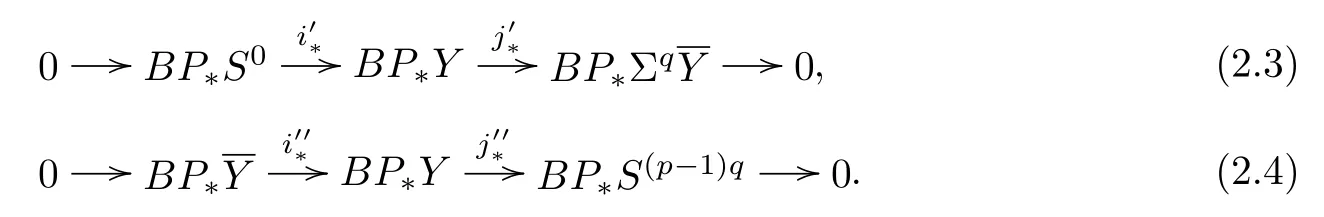
Putting(2.3)and(2.4)together,one has the following long exact sequence:
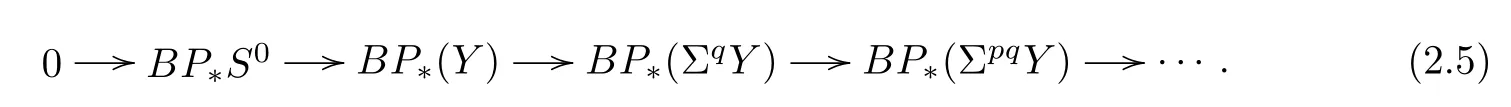
Putting(2.1)and(2.2)together,one has the following Adams diagram of cofibres:
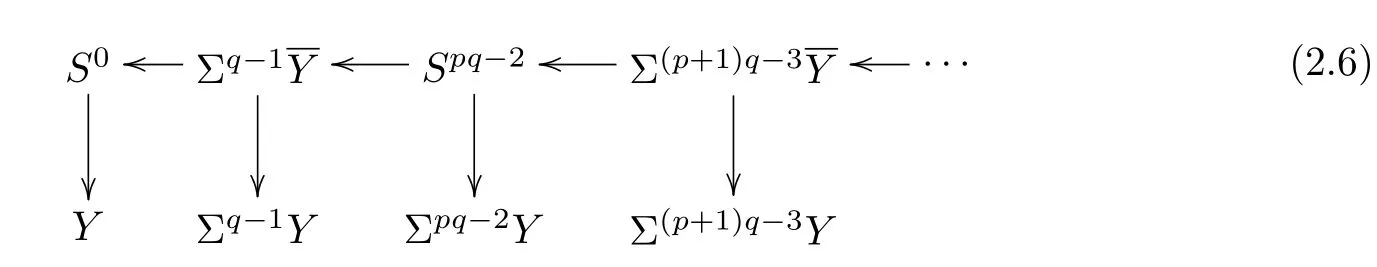
Thus one has the following proposition.
Proposition 2.1(see[14,Proposition 7.4.2]and[15,Theorems 7.1.13 and 7.1.16])Let Y be as above.
(a)There is a spectral sequence converging to(BP∗,BP∗)with the E1-term
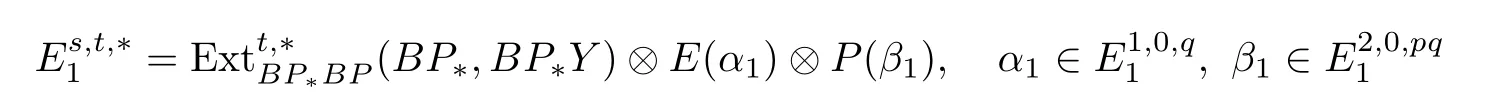
and dr:where E(−)denotes the exterior algebra and P(−)denotes the polynomial algebra on the indicated generators.
This spectral sequence is referred to as the small descent spectral sequence(SDSS).
(b)There is a spectral sequence converging to π∗(S0)with the E1-term
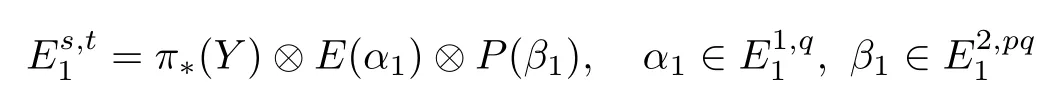
and dr:
This spectral sequence is referred to as the topological small descent spectral sequence(TSDSS).
The above two spectral sequences produce the(BP∗,BP∗)and(BP∗,BP∗)or the corresponding elements in(S0)by(BP∗,BP∗Y)and(BP∗,BP∗Y).(B,BP∗())(s2)or the corresponding elements inπ∗(S0)are produced by(BP∗,BP∗Y)(s2)as described in the following ABC Theorem.
Note that in the ranget−s
ABC Theorem(see[14–15])For p>2and t−s where A is theZ/p-vector space spanned by where R=0ip−2}},and From the generators ofR,we can obtain precise generators ofCas follows. Leti=jp+m.Thenso we have (1)is represented by forp−1m1,from which we have whereuk=and (2)is represented by forp−1km+11,from which we have where Especiallyis represented by which is an element of order. (3)is represented by forp−2km+11,where (4)is represented by forp−2km0,where Especiallyis represented by which is an element of orderp2. It is known thatare not trivial inπ∗()for 3sp−2,p7.Further,we conjecture that so isThe proof includes complicated calculation.Here we only prove that this conjecture is right fors=3. Letϕ:BP→KZ/pbe the Thom map which induces the Thom reduction map between the Adams-Novikov Spectral Sequence and the Adams Spectral Sequence Then it is known that where(Z/p,Z/p)is constructed by X.Wang and Q.Zheng in[18]. Next we prove thatis not trivial in(Z/p,Z/p)by the May spectral sequence. LetA∗denote the dual modpSteenrod algebra which is isomorphic to where the inner degree ofand that ofτiis+1.Set the May filtration onA∗by=2i−1.Applying the May filtration to the cobar construction(Z/p),we get an increasingly filtered moduleand then there is the May spectral sequence(MSS)which converges to(Z/p,Z/p)with theE1-term where aiandcorrespond respectively to(see[14,Theorem 3.2.5]and[8–9]). One has Ifx∈andy∈then The known May differentialsdare given by From the Thom map,we know thatis represented byup to a nonzero coefficient in theE1-term of MSS.In order to prove that0∈(Z/p,Z/p),it is necessary to guarantee that there is no elementx∈in the MSS such thatdr(x)=That is to say,we need to computeSinceconverges non-trivially toit is easy to show thatshould not be killed by some first May differential from(3.2). Lemma 3.1In the May spectral sequence,is generated by the following elements: andis generated by the following elements: ProofIn our range,we only need to consider Note that the degree ofis of the formt=q(+···+p+1)+1.If there is a factoraiin the generatorgthengshould containq a’s,wherea∈It is easy to verify that the generators indo not containa. Therefore and the generators ofare of the form where 0k02p+2,0k14 and 0k26 3. The cohomology ofE(:i+j3)was already computed by Toda in[17].We list these elements in the Table 1 below. Table 1 H∗(E(:i+j 3)) Table 1 H∗(E(:i+j 3)) Generators (s,t/q)1(0,0)h1,0 (1,1)h1,1 (1,p)h1,2 (1,p2)g0 (2,p+2)k0 (2,2p+1)h1,0h1,2 (2,p2+1)g1 (2,p2+2p)k1=h1,2h2,1 (2,2p2+p)h1,0k0 (3,2p+2)l1=h1,0h2,0h3,0 (3,p2+2p+3)l2=h1,1h2,0h2,1 (3,p2+3p+1)l3=h1,0h1,2h3,0 (3,2p2+p+2)h1,1k1 (3,2p2+2p)γ3=h1,2h2,1h3,0 (3,3p2+2p+1)h1,1l1 (4,p2+3p+3)h1,2l1 (4,2p2+2p+3)m1=h1,1h2,0h2,1h3,0 (4,2p2+4p+2)h1,0γ3 (4,3p2+2p+2)h1,1γ3 (4,3p2+3p+1)h1,0m1 (5,2p2+4p+3)g0γ3 (5,3p2+3p+3)k0γ3 (5,3p2+4p+2)h1,0k0γ3 (6,3p2+4p+3) On the one hand,consider the inner degree ofSincet/qis the multiple of the primep,the inner degree ofxis of the formq(np+3)because On the other hand,sinceandhave an even dimension,so isx. Above all,the inspection of Table 1 shows thatxmust be Noting thatg=has the dimension 2p+2 and degreeq(4+2p+3),it is easy to get that In the same way,we can determine the generators of There are the following higher May differentials in the MSS. Lemma 3.2In the May spectral sequence, ProofWe only prove(i),and another statement can be verified easily in the similar way. To calculate these higher May differentials,we are required to work back in the cobar complex(Z/p)whose tensor product is not commutative,and hence permuting the tensor product will give rise to higher May differentials. Sinceis a permanent cycle in the May spectral sequence,it can be represented by some element in the cobar complex(Z/p),and we letdenote this element.From the formula we obtain that in the filtered cobar complexC∗(Z/p), Applying the formula we achieve permutation betweenandin the cobar complex.Moreover,we can also achieve permutation amongand(see[6]for more details). In conclusion,permutation amongandcan be achieved in the sense modand thus,there is a chain(Z/p)such that mod Applying the following relations in theE1-term of MSS by formula(3.2) one has a chainu2=such that and mod−p+12, Above all,there is a chainu∈(Z/p)such that Notice thatandare sent toandin theE2-term of the May spectral sequence respectively.From Lemma 3.1,we know that Therefore,the following higher May differential follows: Theorem 3.1In the Adams spectral sequence,for p>7, Therefore,in the Adams-Novikov spectral sequence,for p>7, ProofAccording to Lemma 3.1,∈can only be killed byG1=andG2=However,from Lemma 3.2,G1andG2do not killconverges nontrivially to(Z/p,Z/p). By the Thom reduction map it is obtained that Theorem 3.2In the Adams-Novikov spectral sequence, converges nontrivially to ProofFrom Theorem 3.1,it is known that Meanwhile,andconverge nontrivially toπ∗(S0).Therefore,we need to prove thatis not killed by any Adams differential.Using the sparseness of the ANSS,it is sufficient to consider elements in(BP∗,BP∗). Let us see the small descent spectral sequence and the ABC Theorem which describes the generators of(BP∗,BP∗Y)(t>2). It is easy to show that only the elementcan survive to(BP∗,BP∗).However,since=0(see[12])in theE2-term of the ANSS,the relation holds.Thusis not killed byThe theorem is obtained. Letpbe an odd prime number and letBPdenote the Brown-Peterson ring spectrum atp(see[3–4]).We have where the homological degrees ofviandtiare given by Let(BP∗,Γ)be a Hopf algebroid.For anyBP∗(BP)-comoduleM,we write One method of calculating this Ext group is to use the cobar complex.Given any Γ-comoduleMwith coactionψ:M→M⊗Γ,one has Ext∗(M)=where the cobar complexMis the differential graded-module with (sfactors of Γ)and the differentialdof degree+1 given by where the coproduct∆(xi)=andψ(m)= The elementmis sometimes denoted bym[x1|x2|···|xs]for simplicity. LetIn=be the ideal ofBP∗.Then Let Γ =Then(BP∗,Γ)is a Hopf algebroid.Thus,there is a natural isomorphism Theorem 4.1The q(+2p+2)−2dimension stable homology group of V(2)is trivial,i.e., ProofFor complexV(2),there is the Adams-Novikov spectral sequence converging to the stable homotopy groups ofV(2)at the primep, It is known that the inner degreetof theE2-term(BP∗,BP∗V(2))is the multiple ofq=2p−2.In order to consider all possible elements converging toV(2),it is sufficient to consider only those of the forms=2+nqandt=q(p2+2p+2+n)forn0. For computing(BP∗,BP∗(V(2)))(n0),consider the isomorphism Note that we only need to consider elements which have the homotopy degreet−sq(p2+2p+2)−2.Since−2 fori>3,we have the following isomorphism: where Γ′==P(3)[v3],andP(3)is the Hopf algebra Z/p[t1,t2,t3]. Hopf algebroid Γ′=P(3)[v3]has the coproduct and the right unit as follows: Since the right unitin the cobar complexCΓ′(BP∗),there is a natural isomorphism For computing(Z/p,Z/p),i.e.,the cohomology of the Hopf algebraP(3),we can use the modified form of the May spectral sequence introduced in[8–9,15].LetP∗=P(,,···)be the dual of Steenrod’s reduced powers.Then there is the spectral sequencewhich converges towith theE1-term We only need to consider the elementswithi+j3 andwithi+j2,so,the modified MayE2-term istensored with the cohomology of the complex described by Toda in[17].We list its generators in the Table 1 in Section 3. In the ranget−s6q(+2p+2)−2,the-term of the modified May spectral sequence equals In our range,the Adams-Novikov-term forV(2)is isomorphic to(Z/p,Z/p)⊗P(v3)which is a subquotient ofG⊗P).It is easy to verify that forn0 because no element can have both the dimensions 2+nqand the inner degreeq(p2+2p+2+n)inG⊗P(v3). It now follows that the theorem holds from the Adams-Novikov spectral sequence forV(2). It is easily showed that the following theorem holds from the above theorem. Theorem 4.2For p7,s1,the Toda bracket⟩=0. ProofLetbe the composite of the following maps: where the first map is the inclusion of the bottom cell. It is well-known thatis aporder element inand then the Toda bracket⟩is well defined andV(2). Let us useejto denote the projection fromV(2)toS0.Thenγs= As a result, because D.C.Ravenel proved the following proposition(see[14,Proposition 7.5.11]and[15,Proposition 7.6.11]). Proposition 4.1If x is an element in the stable homotopy groups of spheres and satisfies px=0,=0and α1x0,then the following relation holds. ProofFrom the relation between Toda brackets and Massey products,we have the following Toda brackets: On the other hand, Therefore,the proposition holds. It is known thatp=0 sincehas orderp.The condition0 holds as a result of R.Kato and K.Shimomura[5]who got that the elements0 forp7 and the positive integertwithpt(t2−1)using the cohomology of the third Morava stabilizer algebra.Thus we get the following result. Theorem 4.3For s2,p7and ps(s2−1),the following relation holds: Corollary 4.1In the stable homotopy groups of spheresis nontrivial and represents the element ProofIn Section 3,we have already got thatis nontrivial inso isThus the corollary holds. It is known thatare not trivial infor 3sp−2,p7.However,we can prove thatis trivial infor 2sp−2,p7. Corollary 4.2For s2,p7and ps(s2−1), ProofThe result can be easily got sinceand=0 inπ∗(S0). AcknowledgementThe authors would like to express their gratitude to Prof.X.Wang for his suggestions. [1]Adams,J.F.,On the strucure and applications of the Steenrod algebra,Comm.Math.Helv.,32,1958,180–214. [2]Adams,J.F.,Stable Homotopy and Generalised Homology,University of Chicago Press,Chicago,1974. [3]Brown,E.H.and Peterson,F.P.,A spectrum whose Zp-cohomology is the algebra of reducedp-th powers,Topology,5,1966,149–154. [4]Cohen,R.L.,Odd Primary Infinite Families in Stable Homotopy Theory,Mem.Amer.Math.Soc.,30/242.D,Amer.Math.Soc.,Providence,1981. [5]Kato,R.and Shimomura,K.,Products of greek letter elements dug up from the third morava stabilizer algebra,Algebr.Geom.Topol.,12,2012,951–961. [6]Liu,X.and Wang,X.,A four-filtered May spectral sequence and its applications,Acta Math.Sin.,Engl.Ser.,24,2008,1507–1524. [7]Liulevicius,A.,The factorization of cyclic reduced powers by secondary cohomology operations,Mem.Amer.Math.Soc.,42,1962,1–112. [8]May,J.P.,The cohomology of restricted Lie algebras and of Hopf algebras;Applications to the Steenrod algebra,Theses,Princeton,1964. [9]May,J.P.,The cohomology of restricted Lie algebras and of Hopf algebras,J.Algebra,3,1966,123–146. [10]Miller,H.,Ravenel,D.C.and Wilson,S.,Periodic phenomena in the Adams-Novikov spectral sequence,Ann.of Math.,106,1977,469–516. [11]Novikov,S.P.,The metods of algebraic topology from the viewpoint of cobordism theories(in Russian),Izv.Akad.Nauk.SSSR.Ser.Mat.,31,1967,855–951. [12]Oka,S.and Shimomura,K.,On products of theβ-element in the stable homotopy of spheres,Hiroshima Math.J.,12,1982,611–626. [13]Ravenel,D.C.,The Adams-NovikovE2-term for a complex withp-cells,Amer.J.Math.,107(4),1985,933–968. [14]Ravenel,D.C.,Complex Cobordism and Stable Homotopy Groups of Spheres,Academic Press,New York,1986. [15]Ravenel,D.C.,Complex cobordism and stable homotopy groups of spheres,A.M.S.Chelsea Publishing,Providence,RI,2004. [16]Ravenel,D.C.,The method of infinite descent in stable homotopy theory,I,Recent Progress in Homotopy Theory(Baltimore,MD,2000),Contemp.Math.,293,Amer.Math.Soc.,Providence,RI,2002,251–284. [17]Toda,H.,On spectra realizing exterior parts of Steenord algebra,Topology,10,1971,55–65. [18]Wang,X.and Zheng,Q.,The convergence ofSci.China Ser.A,41,1998,622–628.
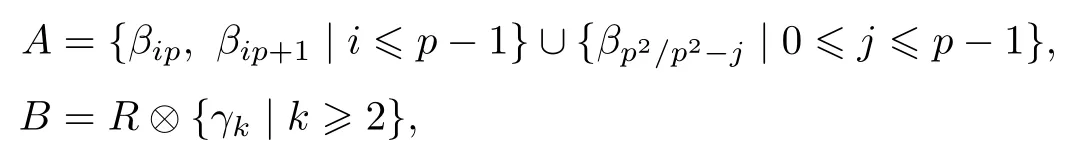
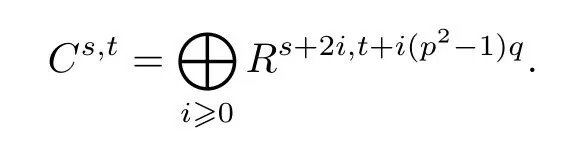
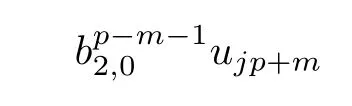


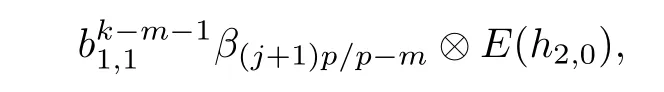
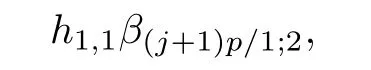
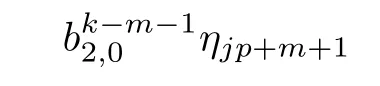
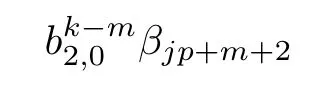
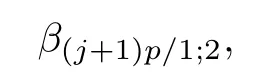
3 The Non-triviality ofin π∗(S0)
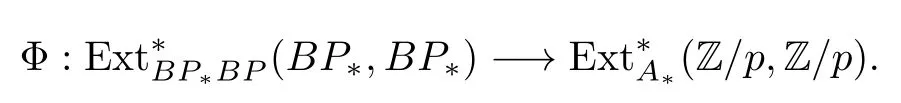

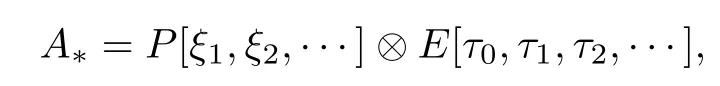

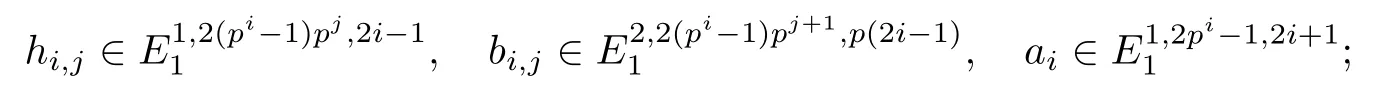

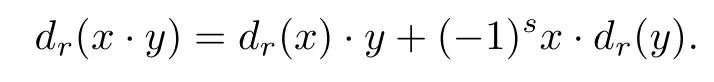
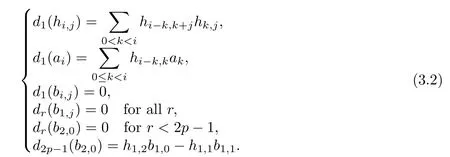


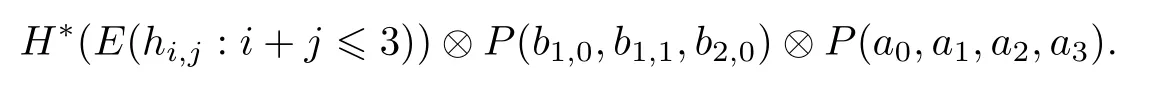
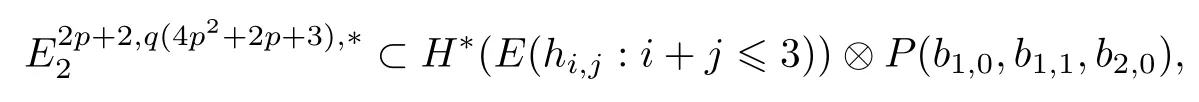

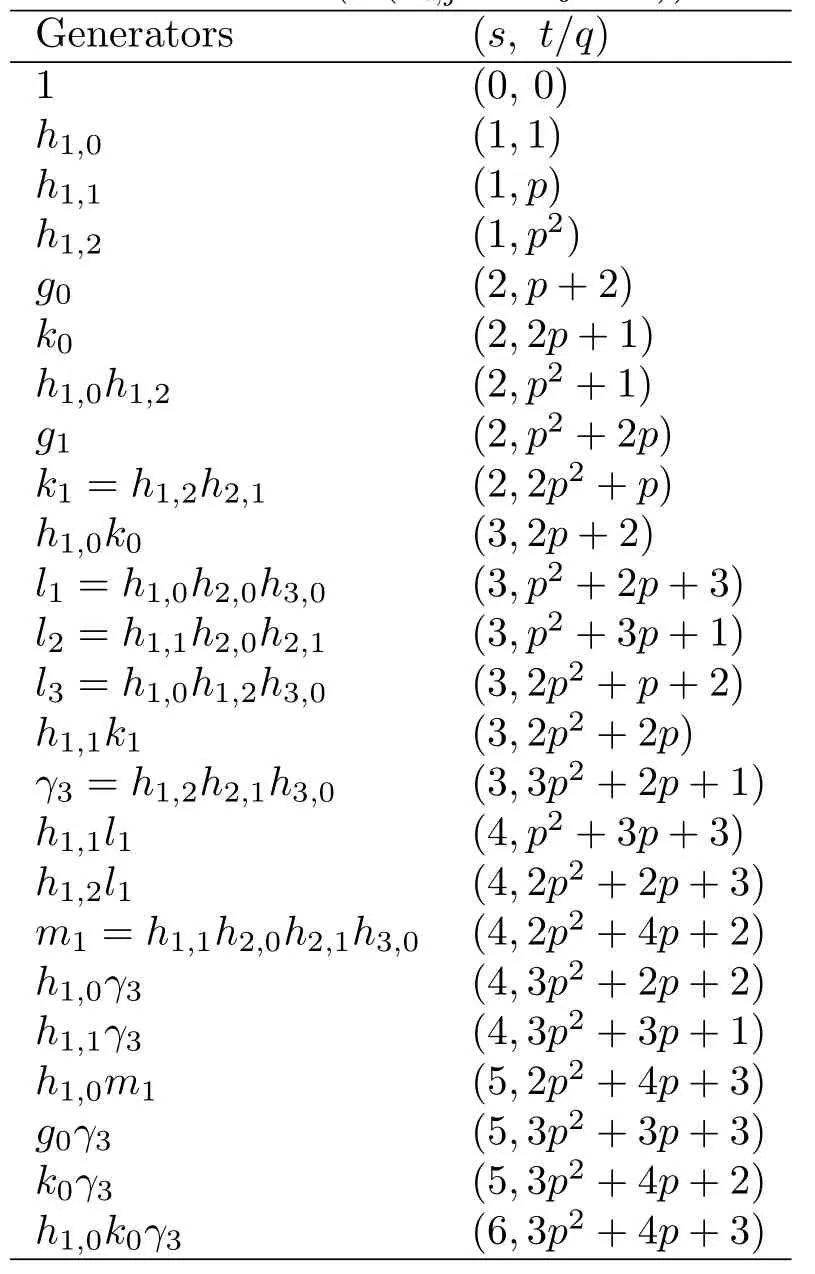



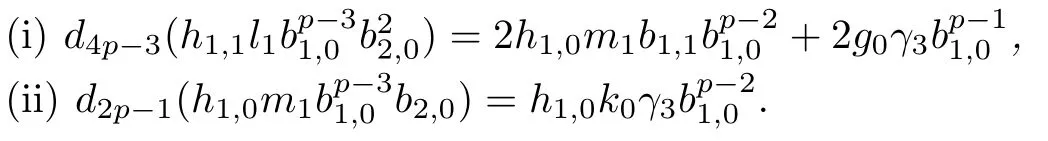

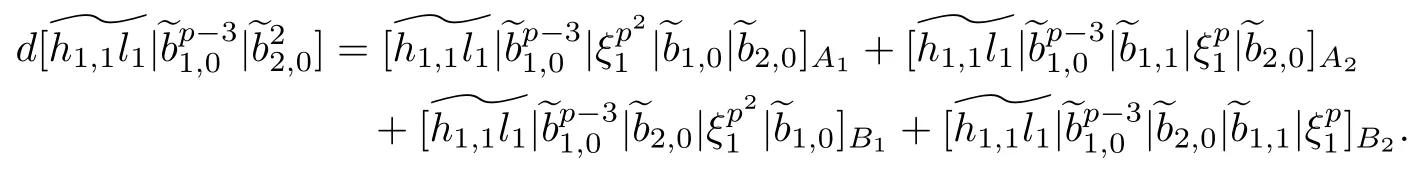


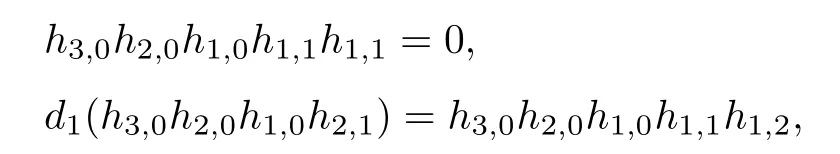
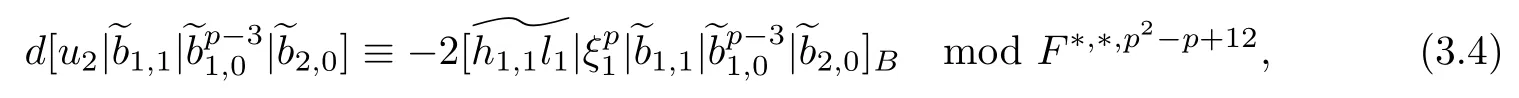
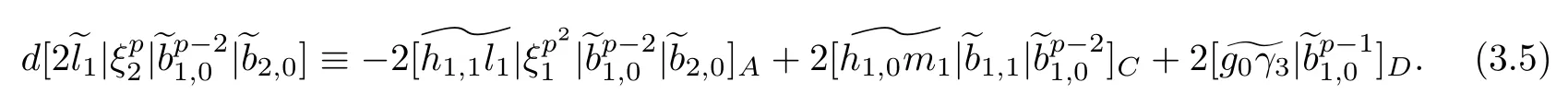

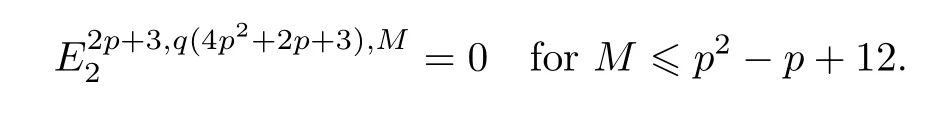


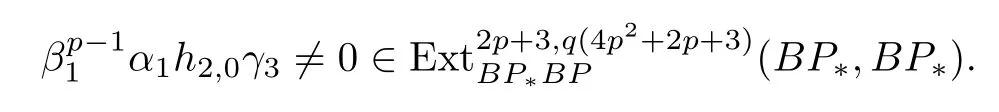

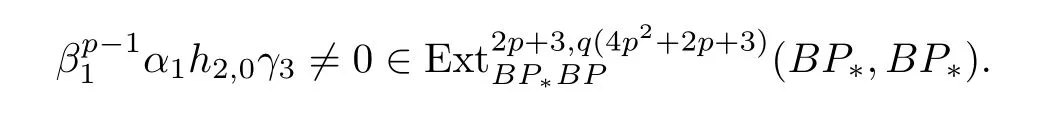

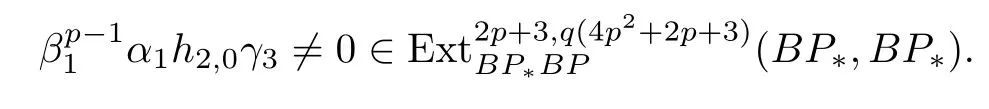
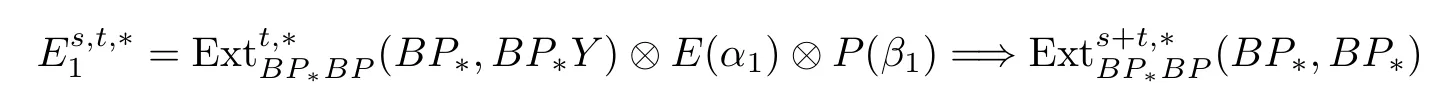

4 A Toda Bracket and Relative Results


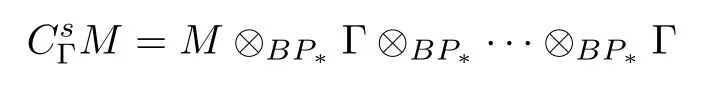


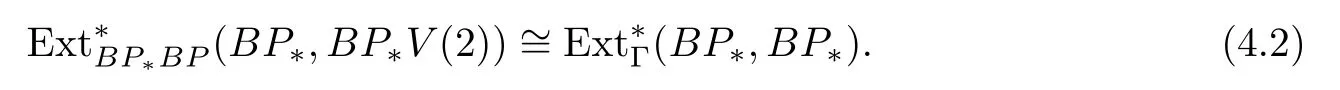


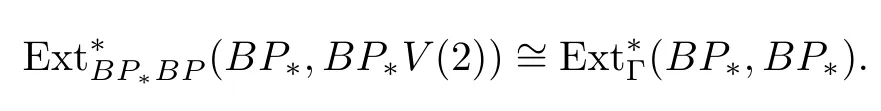

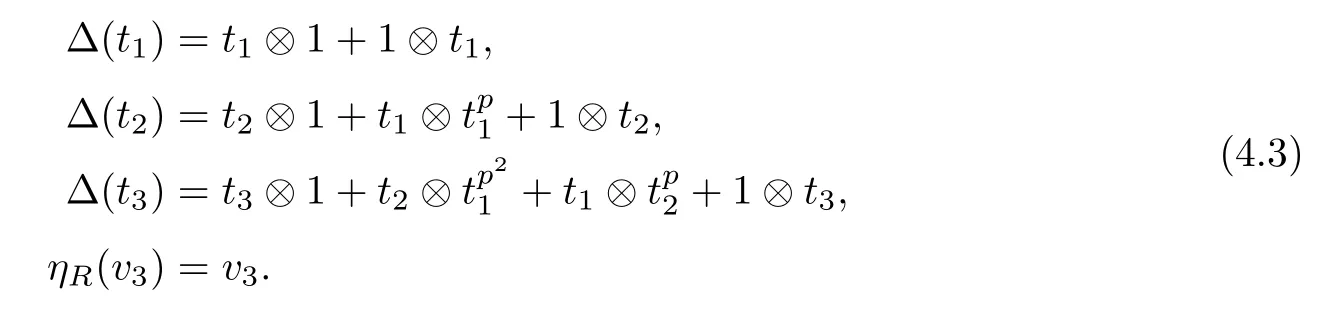

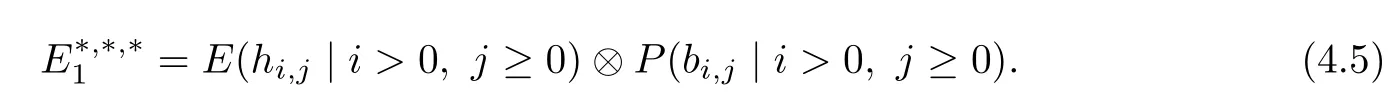
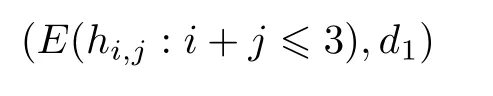
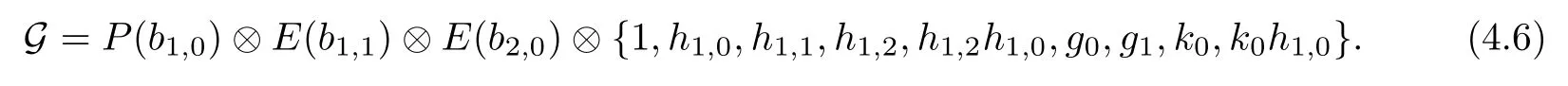
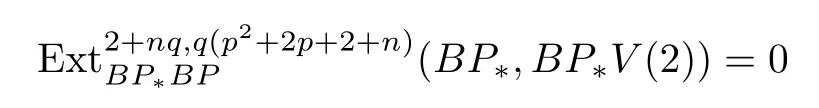
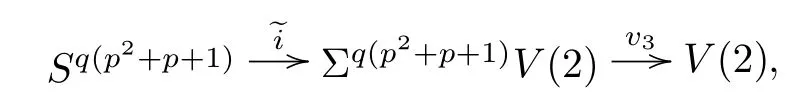

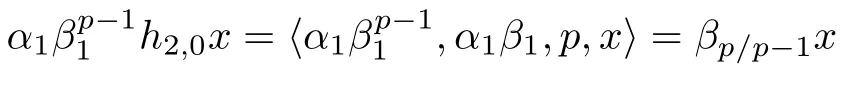
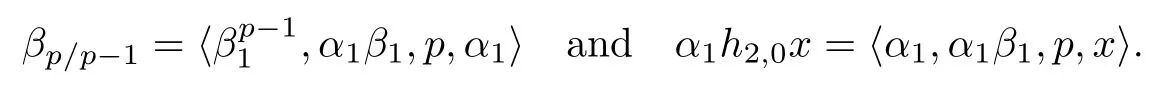

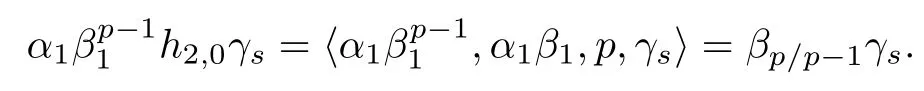
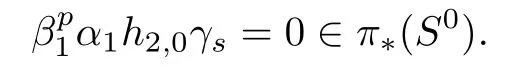
 Chinese Annals of Mathematics,Series B2015年3期
Chinese Annals of Mathematics,Series B2015年3期
- Chinese Annals of Mathematics,Series B的其它文章
- Superderivation Algebras of Modular Lie Superalgebras of O-Type∗
- Convolutions,Tensor Products and Multipliers of the Orlicz-Lorentz Spaces∗
- Lie Bialgebras of Generalized Loop Virasoro Algebras∗
- Vertex Representations of Toroidal Special Linear Lie Superalgebras∗
- Spherical Scattered Data Quasi-interpolation by Gaussian Radial Basis Function∗
- Almost Linear Nash Groups∗
