Spherical Scattered Data Quasi-interpolation by Gaussian Radial Basis Function∗

Zhixiang CHEN Feilong CAO

1 Introduction

Let S2be the unit sphere in a Euclidean space R3defined by

For a target functionfdefined on the sphere,a set of scattered pointsxi,i=1,2,···,n,lying on S2,and associated valuesfi,i=1,2,···,n,we try to find a smooth functionsdefined on S2by means of the data(xi,fi),such thatscan approximate the target functionf.This problem is called scattered data fitting on the sphere,and arises in many areas,including geophysics and meteorology,where the sphere S2is usually taken as a model of the Earth.To solve the problem,several methods have been proposed(see[7]).In these methods,one of the important methods is the interpolation based on linear combinations of spherical radial basis functions.Up to now,there have been a lot of results on the topic.We refer the readers to[4–5,9,12–16,21–23,25–28].

In the Euclidean space Rn,the Gaussian radial basis function defined by

is usually used to be a tool for constructing approximants to approximate the functions defined on the subset of Rn.Particularly,in the approximation and fitting of scattered data,the Gaussian radial basis function has taken an important role(see[1–3,18,20,26,28]).On the sphere S2,the corresponding spherical Gaussian radial basis function(or called the zonal basis function)is defined by

wherexydenotes the Euclidean inner product ofx,y.Usually,(t∈[−1,1])is called spherical Gaussian kernel(see[5,14]).

In general,if there exists a reproducing kernel Hilbert space resulted from a kernel,then the space is called a native space.When a target functionfis in the native space,the error analysis has been completed.Yet,whenfis outside the native space,this time there arises the so called “native space barrier” problem.It is an interesting and important topic,and has been discussed in much literature(see[4,12–16,22–23]).For example,in the recent articles(see[12–13,27]),Le Gia,Sloan,and Wendland constructed approximants of functions outside the native space by means of a kernel.

In this article,we intend to discuss this problem.Our main aim is to study the constructive approximation for scattered data by means of a spherical Gaussian kernel.

The article is organized as follows.In the next section,we will state some preliminary results containing spherical harmonics and the native space.In Section 3,we probe into some problems about the interpolation and approximation by linear combinations of Gaussian radial functions.In Section 4,we will construct quasi-interpolation operators by Gaussian radial functions,and will get the degrees of approximation for continuous functions defined on S2.In Section 5,we will construct an interpolant to continuous functions,and will obtain the error estimates.Finally,we will briefly discuss the construction and approximation of quasi-interpolation operators with local compact support.

2 Preliminaries

For a functionϕ:[−1,1]→R,we set

A functionK(x,y)defined on S2×S2is called a positive definite kernel,if for any finite subsetXof S2,and arbitrary real numbers,ξ∈X,there holds

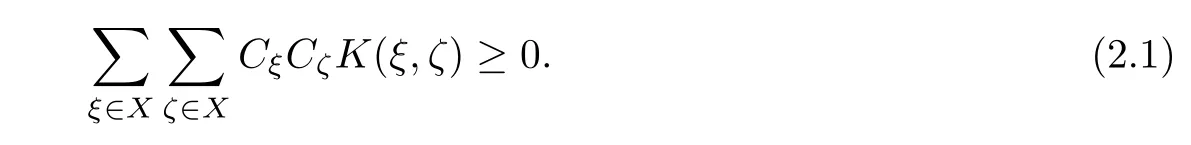
If(2.1)is positive whenever theCξare not all zero,thenK(x,y)is called strictly positive definite,and we also sayϕis strictly positive definite.

Positive definite functions on spheres were first introduced and characterized by Schoenberg in[24],where it was showed that the necessary and sufficient condition of a continuous functionϕbeing positive definite on S2is thatϕis expressible in the form

wherePkis Legendre polynomial with(1)=1,and in fact,akis the Fourier-Legendre coefficient ofϕ.Ifak>0 for allk,thenϕis strictly positive definite(see[6,29]).Strictly positive definite functions are both theoretically interesting and practically important,because they are used to reconstruct an unknown function from scattered data by the interpolation of the form

Below,we introduce the native spaceNϕassociated withϕ.LetL2(S2)be the real Hilbert space equipped with the inner product

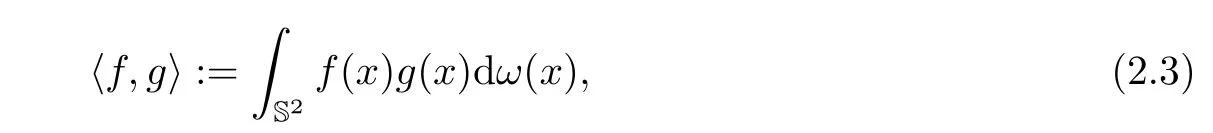
whereωdenotes the Lebesgue surface measure on.We will use=1,2,···,2l+1 to denote the usual orthonormal basis of spherical harmonics(see[8,19,25]).The class of all spherical harmonics of degree at mostnwill be denoted by Πn.Iff∈L2(S2),then we may expand it in a series of spherical harmonics,

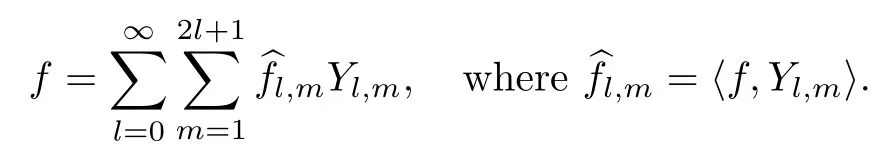
Now we set(t):=Narcowich et al.[21]obtained forl≥0,

Then,the native spaceis defined as

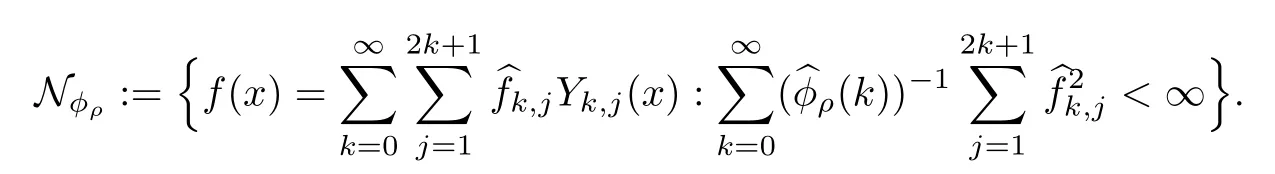
The native spaceis a Hilbert space with the inner product:

Moreover,the space is a reproducing kernel Hilbert space,and the reproducing kernel is(xy)(see[15,21,26]).From[21],we know that the native spaceis contained in a Sobolev spacefor alls,which shows that the functions inhave sufficient smoothness.However,the target functions usually have less smoothness.So it is important and necessary to discuss further the “native space barrier”problem.

We denote the spherical cap with the centerxand the radiusrbyC(x,r).Given a finite setX⊂S2,we define its mesh norm(or fill distance)hXand the separation radiusqXto be

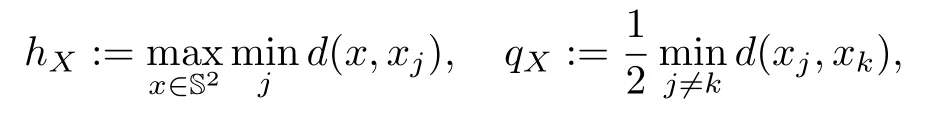
respectively,whered(x,y)is the geodesic distance between the pointsxandyin S2.The mesh ratio defined bymeasures the uniformity of the distribution ofX.Obviously,≥1.We say that the point setXis quasi-uniformly distributed,or simplyXis quasi-uniform if there exists a constantcq>0 independent ofXsuch that

3 Some Discussions on Approximation by Gaussian Kernel

In this article,we consider that the target functionfis inC(S2),the continuous function space with uniform norm∥·∥.LetX=⊂S2,andf∈C(S2).Then we can choose suitableck∈R,k=1,2,···,N,such that the function defined by

interpolatesfonX.SinceIXf(x)∈Nϕ,we use spherical harmonics as an intermediary to estimate the errorf(x)−IXf(x).To show it,we will use a present and classic technique in the following.

It follows from Theorem 3.1 of[23](takingβ=3)that there exists a spherical harmonicpLwith the following properties:

(a)pL∈ΠL,whereL=(L=⌈a⌉denotes the smallest integer≥a),andMis a constant independent off,L,andX;

(b)pL(xi)=f(xi),xi∈X,i=1,2,···,N;

(c)∥f−pL∥≤4dist(f,ΠL).

Then

From(b)and(c),the inequality(3.2)becomes

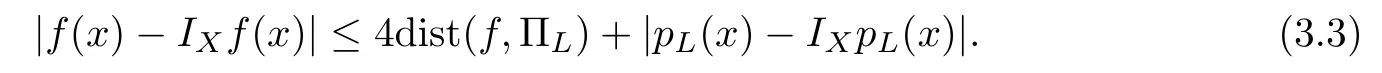
From Theorem 17 of[27],it follows that

We first estimate(l)(2l+1).From(2.4),we have

Using the asymptotic equation(see[11,p.400])

we see that

where we use the inequality(see[11,p.92]).Differing from the casef∈Nϕ,the value ofcan change withL,which implies thatmay be very large.Also,

may not hold.In fact,we expand

and we find that

is in expansion,wheredenotes the projective ofpLon HL(the class of all spherical harmonics with degreeL).

So we look forward to the more detailed analysis on the estimates of

On the other hand,we can use the formto interpolate scattered data.To obtain the coefficientsα1,α2,···,αN,one is required to solve a large scale system of linear equations.The most important advantage of quasi-interpolation is that we can evaluate the approximant directly without the need to solve any linear system of equations.

However,for givenρ,we have

which means that for functionf(x)≡1∈and the error of quasi-interpolation atx=x1,

is not arbitrarily small whenNis sufficiently large.So whenthe form of quasiinterpolation

is invalid.Moreover,the native spaceis too small.Hence we intend to investigate other forms of the quasi-interpolation approximation on the continuous function spaceC(S2)with the help of the kernel

4 Approximation by Quasi-interpolation Operators

Forf∈C(S2),we construct the quasi-interpolation operators

Now we prove the error estimates for the quasi-interpolation operators.

Theorem 4.1Let X=and f∈C(S2).If the mesh norm hXof X satisfiesthen there holds

where ω(f,2hX)denotes the modulus of continuity of f defined by(see[17,25])

ProofObviously,

For anyx∈S2,there existsj0∈N and 1≤j0≤N,such thatx∈Hence,

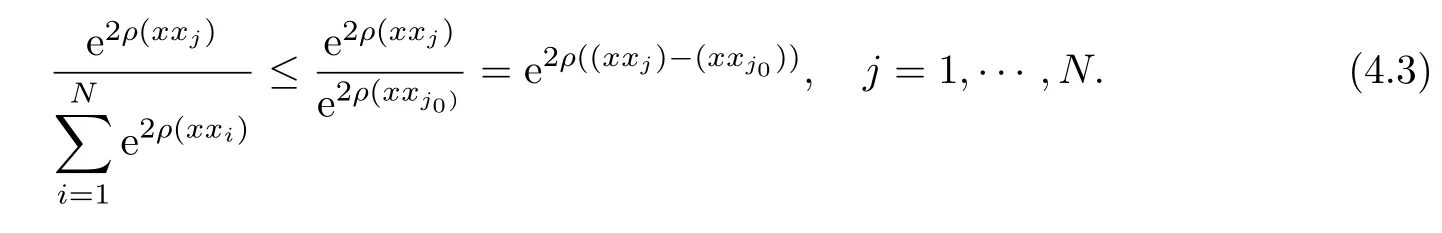
Since

and

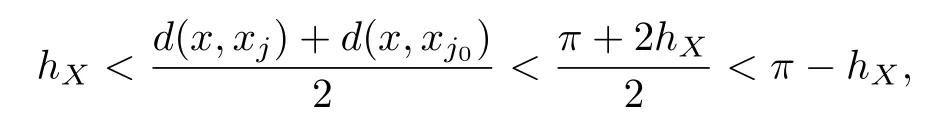
we have

Combining(4.3)–(4.5)leads to

Therefore,for anyx∈S2,one has

which shows

The proof of Theorem 4.1 is completed.

Clearly,if we takeρ=N,then(4.2)becomes

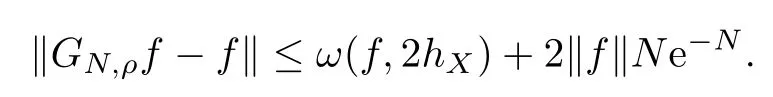
5 Approximation by Interpolation Operators

From the strictly positive definiteness ofit follows that the matrix

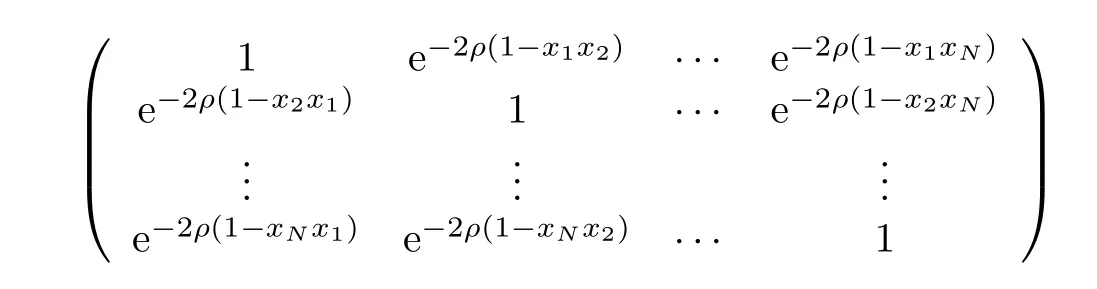
is nonsingular.So it is not difficult to see that the matrix

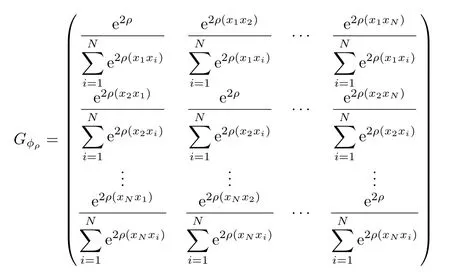
is also nonsingular.This shows that the operators

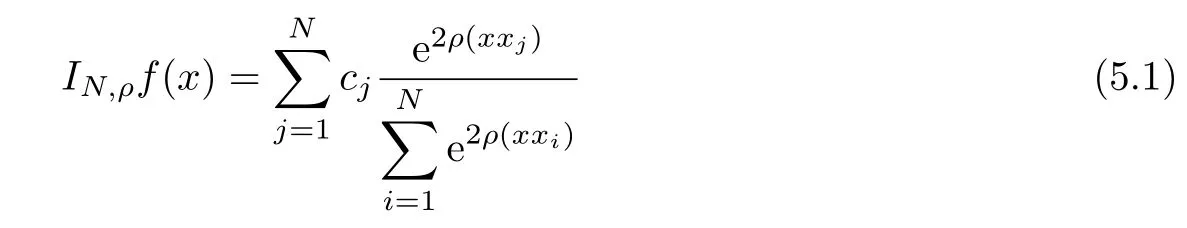
can be an interpolant for the data pointsi=1,2,···,N.

Our target is to estimate the errorf(x)−At first,we introduce some definitions and notations.Let

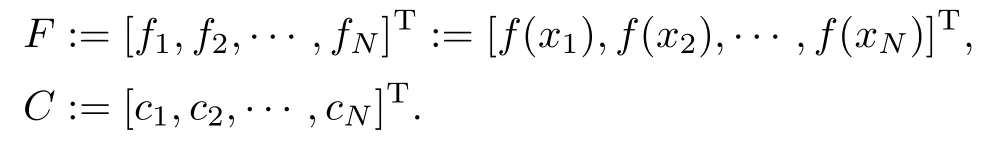
Define the norms of vectorFand matrixas follows:

respectively.LetEbe anN×Nidentity matrix,δEbe the difference ofandE,i.e.,δE=−E,andδFbe the difference ofCandF,i.e.,δF=C−F.Then

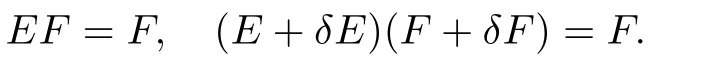
From(5.2),we have

When<1,by Theorem 5.3 of[10],we obtain

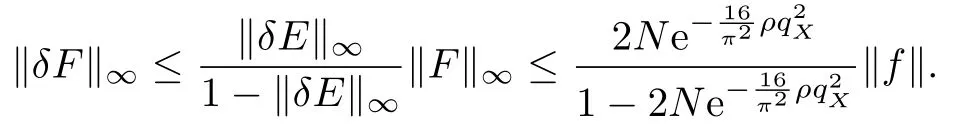
Therefore

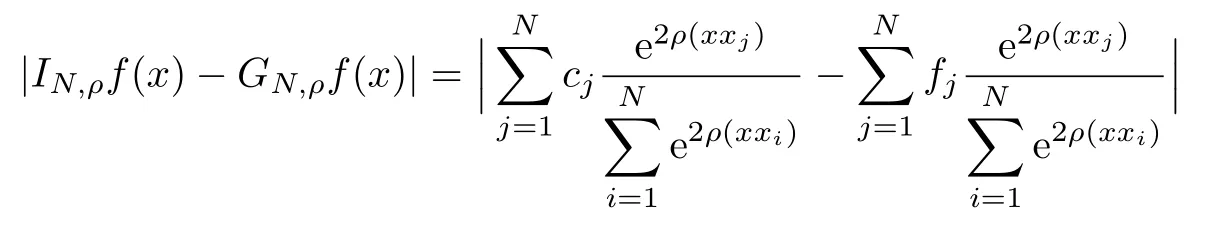
From

we get

Hence,we have proved the following result.

Theorem 5.1Let X=and andbe the mesh norm and the separation radius of X,respectively.If f∈C()andthen there holds

WhenXis quasi-uniform,that is,(2.5)holds,we can chooseρand the result of Theorem 5.1 becomes

Particularly,whenX={,,···,xN}satisfiescq=we have

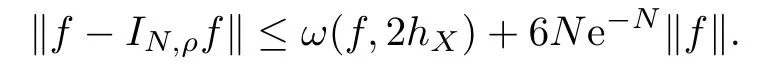
Remark 5.1Using the methods in Section 4 and Section 5,we can extend the Gaussian kernel to general cases.

6 Approximation by Quasi-interpolation Operators with Local Compact Support

We have discussed the approximation off∈C(S2)by the combinations of

Clearly,each function(j=1,2,···,N)is continuous on S2.Now we slightly relax the condition of continuity,and the error estimates will be improved for compensation.

For a given mesh normhXof a finite setX⊂S2,we define

and introduce the quasi-interpolation operators

Thus

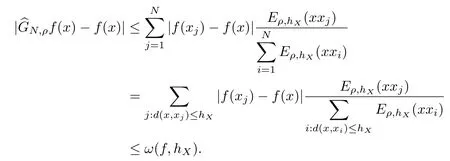
Although the function(t)is discontinuous athX,the oscillationbecomes sufficiently small withρbeing large enough.

In fact,we can give the estimate of the number of pointxjwhich satisfies

as follows:

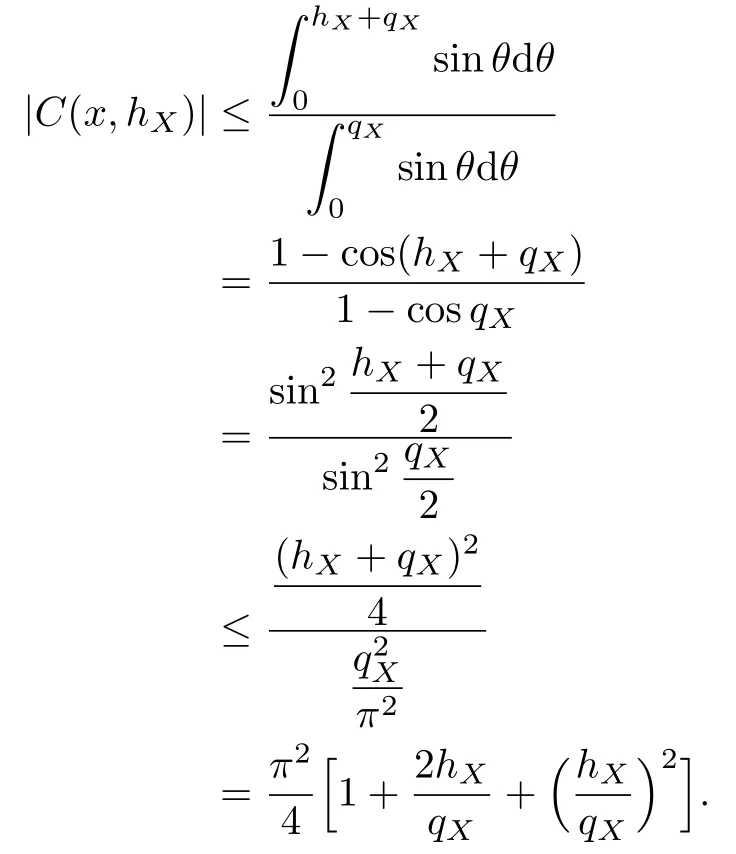
WhenXis quasi-uniform,then

Remark 6.1Naturally,we can use the technique to construct quasi-interpolation operators by means of the kernels with continuous compact support.We also refer the reader to[3,5,26,28].

AcknowledgementThe authors are very grateful to the referees’suggestions and comments on the improvement of the paper.

[1]Boyd,J.P.,Error saturation in Gaussian radial basis function functions on a finite interval,J.Comput.Applied Math.,234,2010,1435–1441.

[2]Boyd,J.P.and Wang,L.,An analytic approximation to the cardinal functions of Gaussian radial basis functions on a one-dimensional infinite uniform lattice,Appl.Math.Comput.,215,2009,2215–2223.

[3]Buhmann,M.D.,Radial Basis Functions:Theory and Implementations,Cambridge Monographs on Applied and Computational Mathematics,Vol.12,Cambridge University Press,Cambridge,UK,2003.

[4]Cao,F.L.,Guo,X.F.and Lin,S.B.,Lperror estimates for scattered data interpolation on spheres,Numerical Functional Analysis and Optimization,32(12),2011,1205–1218.

[5]Cavoretto,R.and De Rossi,A.,Fast and accurate interpolation of large scattered data sets on the sphere,J.Comput.Appl.Math.,234,2010,1505–1521.

[6]Chen,D.,Menegatto,V.A.and Sun,X.,A necessary and sufficient condition for strictly positive definite functions on spheres,Proc.Amer.Math.Soc.,131,2003,2733–2740.

[7]Fasshauer,G.and Schumaker,L.L.,Scattered data fitting on the sphere,Mathematical Methods for Curves and Surfaces II(M.Dæhlen,T.Lyche and L.L.Schumaker,eds),Vanderbilt University Press,Nashville,1998.

[8]Freeden,W.,Gervens,T.and Schreiner,M.,Constructive Approximation on the Sphere,Oxford University Press,New York,1998.

[9]Jetter,K.,Stöckler,J.and Ward,J.,Error estimates for scattered data interpolation on spheres,Math.Comput.,68,1999,733–747.

[10]Kress,R.,Numerical Analysis,Springer-Verlag,New York,1998.

[11]Kuang,J.C.,Applied Inequalities,Shandong Science and Technology Press,Jinan,2004(in Chinese).

[12]Le Gia,Q.T.,Sloan,I.H.and Wendland,H.,Multiscale analysis in Sobolev spaces on the sphere,SIAM J.Numerical Analysis,48,2010,2065–2090.

[13]Le Gia,Q.T.,Sloan,I.H.and Wendland,H.,Multiscale analysis for functions in arbitrary Sobolev spaces by scaled radial basis functions on the unit sphere,Applied Computational Harmonic Analysis,32,2012,401–412.

[14]Le Gia,Q.T.and Tran,T.,An overlapping additive Schwarz preconditioner for interpolation on the unit sphere with spherical radial basis functions,J.Complexity,26,2010,552–573.

[15]Levesley,J.and Sun,X.,Approximation in rough native spaces by shifts of smooth kernels on spheres,J.Approx.Theory,133,2005,269–283.

[16]Levesley,J.and Sun,X.,Corrigendum to and two open questions arising from the article Approximation in rough native spaces by shifts of smooth kernels on spheres,J.Approx.Theory,138,2006,124–127.

[17]Lorentz,G.G.,Approximation of Functions,Holt,Rinehart and Winston,1966.

[18]Maya,V.and Schmidt,G.,Approximate Approximations,American Mathematical Society,Providence,2007.

[19]Müller,C.,Spherical Harmonics,Lecture Notes in Mathematics,Vol.17,Springer-Verlag,Berlin,1966.

[20]Müller,F.and Varnhorn,W.,Error estimates for approximate approximation with Gaussian kernels on compact intervals,J.Approx.Theory,145,2007,171–181.

[21]Narcowich,F.J.,Sun,X.and Ward,J.D.,Approximation power of RBFs and their associated SBFs:A connection,Adv.Comput.Math.,27,2007,107–124.

[22]Narcowich,F.J.,Sun,X.P.,Ward,J.D.and Wendland,H.,Direct and inverse sobolev error estimates for scattered data interpolation via spherical basis functions,Found.Comput.Math.,7,2007,369–390.

[23]Narcowich,F.J.and Ward,J.D.,Scattered data interpolation on spheres:Error estimates and locally supported basis function,SIAM J.Math.Anal.,33,2002,1393–1410.

[24]Schoenberg,I.J.,Positive definite functions on spheres,Duke Math.J.,9,1942,96–108.

[25]Wang,K.Y.and Li,L.Q.,Harmonic Analysis and Approximation on the Unit Sphere,Science Press,Beijing,2000.

[26]Wendland,H.,Scattered Data Approximation,Cambridge University Press,Cambridge,UK,2005.

[27]Wendland,H.,Multiscale analysis in Sobolev spaces on bounded domain,Numerische Mathematik,116,2010,493–517.

[28]Wu,Z.M.,Models,Methods and Theory of Scattered Data Fitting,Science Press,Beijing,2007(in Chinese).

[29]Xu,Y.and Cheney,E.W.,Strictly positive definite functions on spheres,Proc.Amer.Math.Soc.,116,1992,977–981.