Almost Linear Nash Groups∗
Binyong SUN
1 Introduction
Basic notions and properties concerning Nash manifolds are reviewed in Section 2.In this introduction,we introduce some basic notions concerning Nash groups.See Section 3 for more details.
A Nash group is a group which is simultaneously a Nash manifold so that all group operations are Nash maps.A Nash homomorphism is a group homomorphism between two Nash groups which is simultaneously a Nash map.If a Nash homomorphism is bijective,then its inverse is also a Nash homomorphism.In this case,we say that the Nash homomorphism is a Nash isomorphism.Two Nash groups are said to be Nash isomorphic to each other if there exists a Nash isomorphism between them.
Given a subgroup of a Nash groupG,if it is semialgebraic,then it is automatically a closed Nash submanifold ofG(see Proposition 3.1).In this case,we call it a Nash subgroup ofG.A Nash subgroup is canonically a Nash group.
As usual,all finite-dimensional real representations of Lie groups are assumed to be continuous.A Nash representation is a finite-dimensional real representation of a Nash group such that the action map is a Nash map.
Definition 1.1A Nash group is said to be almost linear if it has a Nash representation with a finite kernel.
Almost linear Nash groups form a nice class of mathematical objects.Their structures are simpler than those of general Lie groups,and in the study of infinite-dimensional representation theory,they are more flexible than linear algebraic groups.Although there is a vast literature on Lie groups and linear algebraic groups,it seems that almost linear Nash groups have not been systematically studied(see[17]for a brief introduction to Nash groups).The goal of thisarticle is to provide a detailed study of structures of almost linear Nash groups,for possible later reference.The structure theory of almost linear Nash groups is similar to that of linear algebraic groups.However,we try to avoid the language of algebraic geometry to keep the article as elementary as possible.In what follows,we summarize some basic results about almost linear Nash groups which are either well-known or will be proved in this article.
It is clear that a Nash subgroup of an almost linear Nash group is an almost linear Nash group.The product of two almost linear Nash groups is an almost linear Nash group.By the following proposition,the quotient of an almost linear Nash group by a Nash subgroup is canonically an affine Nash manifold,and the quotient by a normal Nash subgroup is canonically an almost linear Nash group.
Proposition 1.1Let G be an almost linear Nash group,and H be a Nash subgroup of it.Then there exists a unique Nash structure on the quotient topological space G/H which makes the quotient map G→G/H a submersive Nash map.With this Nash structure,G/H becomes an affine Nash manifold,and the left translation map G×G/H→G/H is a Nash map.Furthermore,if H is a normal Nash subgroup of G,then the topological group G/H becomes an almost linear Nash group under this Nash structure.
For each normal Nash subgroupHof an almost linear Nash groupG,the Nash groupG/His called a Nash quotient group ofG.
There are three classes of almost linear Nash groups which are basic to the general structure theory,namely,elliptic Nash groups,hyperbolic Nash groups and unipotent Nash groups.
Definition 1.2A Nash group is said to be elliptic if it is almost linear and compact.It is said to be hyperbolic if it is Nash isomorphic tofor some n≥0.It is said to be unipotent if it has a faithful Nash representation such that all group elements act as unipotent linear operators.
Here and as usual,denotes the set of positive real numbers.It is a Nash group in the obvious way.Recall that a linear operatorxon a finite-dimensional vector space is said to be unipotent ifx−1 is nilpotent.
There is no need to say that a Nash group is almost linear if it is elliptic,hyperbolic or unipotent.
Definition 1.3An element of an almost linear Nash group G is said to be elliptic,hyperbolic,or unipotent if it is contained in a Nash subgroup of G which is elliptic,hyperbolic,or unipotent,respectively.
Definitions 1.2–1.3 are related as follows.
Proposition 1.2An almost linear Nash group is elliptic,hyperbolic,or unipotent if and only if all of its elements are elliptic,hyperbolic,or unipotent,respectively.
In general,we have the following proposition.
Proposition 1.3Let G be an almost linear Nash group.If G is elliptic,hyperbolic or unipotent,then all Nash subgroups and all Nash quotient groups of G are elliptic,hyperbolic or unipotent,respectively.If G has a normal Nash subgroup H so that H and G/H are both elliptic,both hyperbolic or both unipotent,then G is elliptic,hyperbolic or unipotent,respectively.
Concerning elliptic Nash groups,we have the following theorem.
Theorem 1.1The followings hold true:
(1)Every compact Lie group has a unique Nash structure on its underlying topological space which makes it an almost linear Nash group.
(2)Every continuous homomorphism from an elliptic Nash group to an almost linear Nash group is a Nash homomorphism.
(3)Every compact subgroup of an almost linear Nash group is a Nash subgroup.
Theorem 1.1 implies that the category of elliptic Nash groups is isomorphic to the category of compact Lie groups.
Recall that a subgroup of a Lie groupGis said to be analytic if it is equal to the image of an injective Lie group homomorphism from a connected Lie group toG.Every analytic subgroup is canonically a Lie group(this is implied by[18,Theorem 1.62]).
For unipotent Nash groups,we have the following theorem.
Theorem 1.2The followings hold true:
(1)As a Lie group,every unipotent Nash group is connected,simply connected and nilpotent.
(2)Every connected,simply connected,nilpotent Lie group has a unique Nash structure on its underlying topological space which makes it a unipotent Nash group.
(3)Every continuous homomorphism between two unipotent Nash groups is a Nash homomorphism.
(4)Every analytic subgroup of a unipotent Nash group is a Nash subgroup.
Theorem 1.2 implies that the category of unipotent Nash groups is isomorphic to the category of connected,simply connected,nilpotent Lie groups.Recall that the later category is equivalent to the category of finite-dimensional nilpotent real Lie algebras.
For everyr∈Q,the map

is a Nash homomorphism fromto itself.Conversely,all Nash homomorphisms fromto itself are of this form.We view the abelian groupas a right Q-vector space so that

for allx∈andr∈Q.Note that for every finite-dimensional left Q-vector spaceE,Eis obviously a hyperbolic Nash group.Moreover,we have the following theorem.
Theorem 1.3The functor
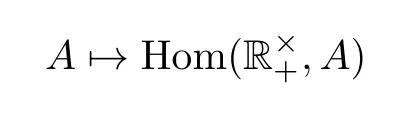
establishes an equivalence from the category of hyperbolic Nash groups to the category of finitedimensional leftQ-vector spaces.It has a quasi-inverse

Here and henceforth,for any two Nash groupsG1andG2,Hom(G1,G2)denotes the set of all Nash homomorphisms fromG1toG2.It is obviously an abelian group whenG2is abelian.The abelian group Hom(,A)of Theorem 1.3 is a left Q-vector space as follows:
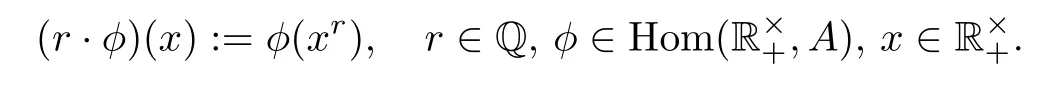
In a way similar to Jordan decompositions for linear algebraic groups,we have the following theorem.
Theorem 1.4Every element x of an almost linear Nash group G is uniquely of the form x=ehu such that e∈G is elliptic,h∈G is hyperbolic,u∈G is unipotent,and they pairwise commute with each other.
We call the equalityx=ehuof Theorem 1.4 the Jordan decomposition ofx.In Section 8,Jordan decompositions at the Lie algebra level are also discussed.
Besides elliptic Nash groups,hyperbolic Nash groups and unipotent Nash groups,there are two other classes of Nash groups which are important to the general structure theory,namely,reductive Nash groups and exponential Nash groups.
Definition 1.4A Nash group is said to be reductive if it has a completely reducible Nash representation with a finite kernel.It is said to be exponential if it is almost linear and has no non-trivial elliptic element.
Here and as usual,a representation is said to be completely reducible if it is a direct sum of irreducible subrepresentations,or equivalently,if each subrepresentation of it has a complementary subrepresentation.
A general reductive Nash group is more or less the direct product of two reductive Nash groups of the particular type,namely,a semisimple Nash group and a Nash torus.
Definition 1.5A Nash group or a Lie group is said to be semisimple if its Lie algebra is semisimple.A Nash torus is a Nash group which is Nash isomorphic tofor some m,n≥0.
Here S denotes the Nash group of complex numbers of modulus one.
Concerning semisimple Nash groups,we have the following theorem.
Theorem 1.5The followings hold true:
(1)Every semisimple Nash group is almost linear.
(2)Every semisimple Nash group has finitely many connected components,and its identityconnected component has a finite center.
(3)Let G be a semisimple Lie group which has finitely many connected components,and whose identity connected component has a finite center.Then there exists a unique Nash structure on the underlying topological space of G which makes G a Nash group.
(4)Every continuous homomorphism from a semisimple Nash group to an almost linear Nash group is a Nash homomorphism.
(5)Every semisimple analytic subgroup of an almost linear Nash group is a Nash subgroup.
Theorem 1.5 implies that the category of semisimple Nash groups is isomorphic to the category of semisimple Lie groups which have finitely many connected components,and whose identity connected components have finite centers.
For every almost linear Nash groupG,define its unipotent radical to be
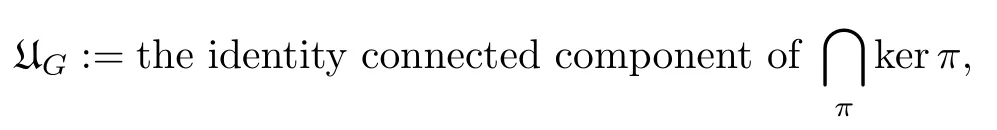
whereπruns through all irreducible Nash representations ofG.This is the largest normal unipotent Nash subgroup ofG(see Proposition 14.1).
We have the following theorem concerning reductive Nash groups.
Theorem 1.6The followings are equivalent for an almost linear Nash group G:
(a)It is reductive.
(b)All Nash representations of G are completely reducible.
(c)The unipotent radical of G is trivial.
(d)For some Nash representations of G with a finite kernel,the attached trace form on the Lie algebra of G is non-degenerate.
(e)For every Nash representation of G with a finite kernel,the attached trace form on the Lie algebra of G is non-degenerate.
(f)The identity connected component of G is reductive.
(g)There exists a connected semisimple Nash group H,a Nash torus T,and a Nash homomorphism H×T→G with a finite kernel and open image.
Here,for every Nash representationVof a Nash groupG,the attached trace formon the Lie algebra g ofGis defined by
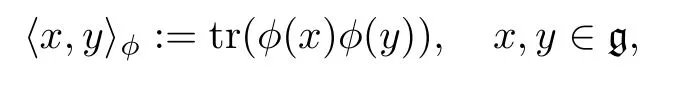
whereϕ:g→gl(V)denotes the differential of the representationVofG.Here and as usual,gl(V)denotes the algebra of all linear endomorphisms ofV;and as quite often,when no confusion is possible,we do not distinguish a representation with its underlying vector space.
Denote by Bn(R)the Nash subgroup of GLn(R)consisting all upper-triangular matrices with positive diagonal entries(n≥0).It is obviously an exponential Nash group.
Theorem 1.7The followings are equivalent for an almost linear Nash group G:
(a)It is exponential.
(b)It has no non-trivial compact subgroup.
(c)It has no proper co-compact Nash subgroup.
(d)The quotient G/UGis a hyperbolic Nash group.
(e)It is Nash isomorphic to a Nash subgroup ofBn(R)for some n≥0.
(f)The exponential map from the Lie algebra of G to G is a diffeomorphism.
(g)Every Nash action of G on every non-empty compact Nash manifold has a fixed-point.
Here a Nash action means an action of a Nash group on a Nash manifold such that the action map is Nash.
The following theorem makes the structure theory of almost linear Nash groups extremely pleasant.
Theorem 1.8Let G be an almost linear Nash group.Then every elliptic(hyperbolic,unipotent,reductive or exponential)Nash subgroup of G is contained in a maximal one,and all maximal elliptic(hyperbolic,unipotent,reductive or exponential)Nash subgroups of G are conjugate to each other in G.
A maximal reductive Nash subgroup of an almost linear Nash groupGis called a Levi component ofG.
Theorem 1.9Let L be a Levi component of an almost linear Nash group G.Then G=L
The equalityG=Lof Theorem 1.9 is called a Levi decomposition ofG.
Theorem 1.10Let G be an almost linear Nash group,K be a maximal elliptic Nash subgroup of G,and B be a maximal exponential Nash subgroup of G.Then the multiplication map K×B→G is a Nash diffeomorphism.
LetG,KandBbe as in Theorem 1.10.LetAbe a Levi component ofB,which is a hyperbolic Nash group.Denote byNthe unipotent radical ofB.Then by Theorems 1.9–1.10,we haveG=KAN.This is called an Iwasawa decomposition ofG.
The author thanks Masahiro Shiota for helpful email correspondences,and for confirming Proposition 2.4.
2 Nash Manifolds
We begin with a review of basic concepts and properties of Nash manifolds which are necessary for this article(see[2,16]for more details).Recall that a subset of(n≥0)is said to be semialgebraic if it is a finite union of the sets of the form

wherer,s≥0,,,···,and,,···,are real polynomial functions on Rn.Forn=−∞,we defineto be the empty set,and its only subset is defined to be semialgebraic.It is clear that the collection of semialgebraic sets in(n≥0 orn=−∞)is closed under taking finite union,finite intersection,and complement.
A mapφ:X→X′from a semialgebraic setX⊂Rnto a semialgebraic set(m≥0 orm=−∞)is said to be semialgebraic if its graph is semialgebraic inTarski-Seidenberg theorem asserts that the image of a semialgebraic set under a semialgebraic map is semialgebraic:Ifφ:X→X′is semialgebraic,thenφ(X0)is semialgebraic for each semialgebraic setX0⊂X.As an easy consequence of Tarski-Seidenberg theorem,we know that the composition of two semialgebraic maps is also semialgebraic;and the inverse image of a semialgebraic set under a semialgebraic map is semialgebraic.
Definition 2.1A Nash structure on a topological space M is an element n∈{−∞,0,1,2,···}together with a set N with the following properties:
(a)The set N is contained inN(Rn,M),whereN(,M)denotes the set of all triples(ϕ,U,U′)such that U is an open semialgebraic subset of,is an open subset of M,and ϕ:U→U′is a homeomorphism.
(b)Every two elementsof N are Nash compatible,namely,the homeomorphism

has a semialgebraic domain and a codomain,and is semialgebraic and smooth.
(c)There are finitely many elementsof N,i=1,2,···,r(r≥0),such that
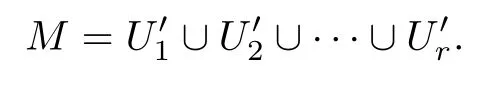
(d)For every element ofN(,M),if it is Nash compatible with all elements of N,then it is an element of N.
(e)If M is empty,then n=−∞.
The following lemma is routine to check.
Lemma 2.1With the notation as in Definition2.1,let

be a finite subset ofN(,M),whose elements are pairwise Nash compatible with each other.If M is non-empty and
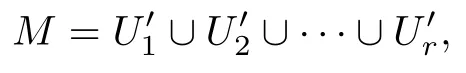
then together with n,the set

is a Nash structure on M.
A Nash manifold is defined to be a Hausdorf ftopological space together with a Nash structure on it.The elementnin Definition 2.1 of the Nash structure is called the dimension of the Nash manifold,and an element ofNin Definition 2.1 of the Nash structure is called a Nash chart of the Nash manifold.
Definition 2.2A continuous map φ:M→N between Nash manifolds is called a Nash map if for all Nash charts(ϕ,U,)of M and(ψ,V,of N,the setis semialgebraic,and the map
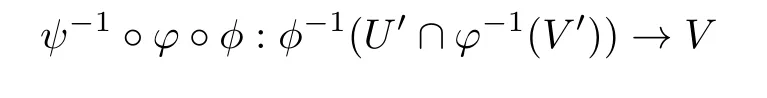
is semialgebraic and smooth.
It is clear that every Nash manifold is a smooth manifold,and every Nash map is a smooth map.The composition of two Nash maps is certainly a Nash map.
Definition 2.3A subset X of a Nash manifold M is said to be semialgebraic ifis semialgebraic for every Nash chartof M.
As in the case of Rn,the collection of semialgebraic sets in a Nash manifold is closed under taking finite union,finite intersection,and complement.Tarski-Seidenberg theorem easily implies the following lemma.
Lemma 2.2Let φ:M→N be a Nash map of Nash manifolds.Then for each semialgebraic subset X of M,the image φ(X)is a semialgebraic subset of N;and for each semialgebraic subset Y of N,the inverse image(Y)is a semialgebraic subset of M.
The following proposition is a useful criterion for a continuous map to be a Nash map.
Proposition 2.1Let φ:M→N be a continuous map of Nash manifolds.Then φis a Nash map if and only if
(1)for each semialgebraic open subset Y of N,the inverse image(Y)is semialgebraic in M,
(2)for every x∈M,there are Nash charts(ϕ,U,U′)of Mand(ψ,V,V′)of N such that x∈U′,φ(U′)⊂V′,and the map

is semialgebraic and smooth.
ProofThis is an easy consequence of[2,Proposition 8.1.8].
The following lemma will be used for several times.
Lemma 2.3Let φ:M→M′be a surjective submersive Nash map of Nash manifolds.Let N be a Nash manifold and let ψ:M′→N be a map.Then ψis a Nash map if and only if ψ◦φ is a Nash map.
ProofThe“only if” part of the lemma is obvious.Using Proposition 2.1 and Lemma 2.2,the “if” part holds because the mapφhas local Nash sections.
Given a Nash map,if it is a diffeomorphism as a map of smooth manifolds,then its inverse is also a Nash map.In this case,we call the Nash map a Nash diffeomorphism.Two Nash manifolds are said to be Nash diffeomorphic to each other if there exists a Nash diffeomorphism between them.
Definition 2.4A semialgebraic locally closed submanifold of a Nash manifold M is called a Nash submanifold of M.
In this article,all locally closed submanifolds of a smooth manifold are assumed to be equidimensional.By the following proposition,every Nash submanifold is automatically a Nash manifold.
Proposition 2.2Let X be a Nash submanifold of a Nash manifold M.Then there exists a unique Nash structure on the topological space X which makes the inclusion XM an immersive Nash map.
We say that a Nash mapφ:M→Nis a Nash embedding ifφ(M)is a Nash submanifold ofN,and the induced mapφ:M→φ(M)is a Nash diffeomorphism.
By the following proposition,the product of two Nash manifolds is again a Nash manifold.
Proposition 2.3Let M and N be two Nash manifolds.Then there exists a unique Nash structure on the topological space M×N which makes the projections M×N→M and M×N→N submersive Nash maps.
Both Propositions 2.2–2.3 are standard.We shall not go to their proofs.
The following lemma is obvious.
Lemma 2.4Let φ:M→N be a smooth map of Nash manifolds.Then φ is a Nash map if and only if its graph is semialgebraic in M×N.
Lemmas 2.2 and 2.4,and the following basic result will be used without further explicit mention.
Lemma 2.5(see[7,Theorem 2.23])Every semialgebraic subset of a Nash manifold has only finitely many connected components and each of them is semialgebraic.
Recall the following lemma.
Lemma 2.6(see[16,Remark I.5.12])Every Nash manifold of dimension n(n≥0)is covered by finitely many open Nash submanifolds which are Nash diffeomorphic toRn.
Using Lemmas 2.5–2.6,it is easy to prove the following lemma.
Lemma 2.7Let φ:M→M′be a submersive Nash map of Nash manifolds.Assume that φ is a finite-fold covering map as a map of topological spaces.Let N be a Nash manifold,and ψ:N→M be a continuous map.Then ψ is a Nash map if and only if φ ◦ ψ is a Nash map.
By the following proposition,a finite-fold cover of a Nash manifold is a Nash manifold.
Proposition 2.4Let N be a Nash manifold,M be a topological space,and φ:M→N be a finite-fold covering map of topological spaces.Then there exists a unique Nash structure on M which makes φ a submersive Nash map.
ProofThis is known to experts.We sketch a proof for the lack of reference.First note thatMis Hausdorf f,sinceNis Hausdorf f.Since this proposition is trivial whenMis an empty set,we assume thatMis non-empty.The uniqueness assertion of this proposition is a direct consequence of Lemma 2.7.In what follows,we construct a Nash structure onMwhich makesφa submersive Nash map.
Write(n,NN)for the Nash structure onN.Put

where
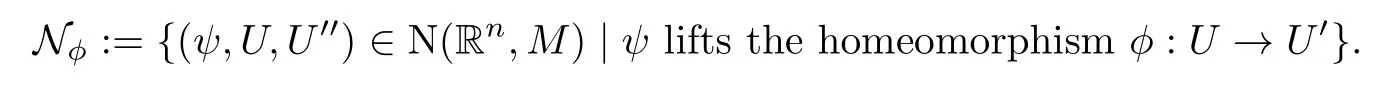
One checks that all elements inare pairwise Nash compatible.Lemma 2.6 implies that the sethas property(c)of Definition 2.1.Denote bythe set of all elements in N(Rn,M)which are Nash compatible with all elements of.Lemma 2.1 implies that(n,)is a Nash structure onM.With this Nash structure,φis clearly a submersive Nash map.
Every finite-dimensional real vector space is obviously a Nash manifold.A Nash manifold is said to be affine if it is Nash diffeomorphic to a Nash submanifold of some finite-dimensional real vector spaces.It is known that every affine Nash manifold is actually Nash diffeomorphic to a closed Nash submanifold of some finite-dimensional real vector spaces(see[17,Section 2.22]).It is clear that a Nash submanifold of an affine Nash manifold is an affine Nash manifold;the product of two affine Nash manifolds is an affine Nash manifold.The following criterion implies that a finite-fold cover of an affine Nash manifold is an affine Nash manifold.
Proposition 2.5(see[16,Proposition III.1.7])Let M be a Nash manifold of dimension n≥0.Then M is affine if and only if for every x∈M,there is a Nash map M→Rnwhich is submersive at x.
Projective spaces form an important family of affine Nash manifolds:For each finitedimensional real vector spaceV,the set P(V)of all one-dimensional subspaces ofVis naturally an affine Nash manifold(see[2,Theorem 3.4.4]).
For each semialgebraic subsetXof a Nash manifoldM,define its dimension
The following properties of the dimensions of semialgebraic sets are obvious(see[7,p.56]):The dimension of the union of fi nitely many semialgebraic sets is the maximum of the dimensions of these semialgebraic sets,and the dimension of a fi nite product of semialgebraic sets is the sum of their dimensions.The following basic facts concerning dimensions of semialgebraic sets are well-known.
Proposition 2.6(see[7,Proposition 3.16 and Theorem 3.20])The followings hold true:
(1)The closureof a semialgebraic set X in a Nash manifold is semialgebraic.Moreover,dim=dimX;anddimX (2)Each semialgebraic subset of a finite-dimensional real vector space has the same dimension as its Zariski closure. Note that all Zariski closed subsets of a finite-dimensional real vector space are semialgebraic. For a semialgebraic setXof a Nash manifoldM,an elementx∈Xis said to be smooth of dimensiond≥0 if there is a semialgebraic open neighborhoodUofxinMsuch thatX∩Uis ad-dimensional Nash submanifold ofM.Note thatXis a Nash submanifold ofMif and only if all points of it are smooth of dimension dimX. Lemma 2.8(see[1,Proposition 5.53])Let X be a non-empty semialgebraic subset of a Nash manifold M.Then X has a point which is smooth of dimensiondimX. In this section,we introduce some generalities on Nash groups and almost linear Nash groups. Definition 3.1A Nash group is a Hausdorf ftopological group G,equipped with a Nash structure on its underlying topological space so that both the multiplication map G×G→G and the inversion map G→G are Nash maps between Nash manifolds.A Nash homomorphism between two Nash groups is a group homomorphism between them which is simultaneously a Nash map. The following basic result will be used freely without further explicit mention. Proposition 3.1Every semialgebraic subgroup of a Nash group G is a closed Nash submanifold of G. ProofThis is well-known.We sketch a proof for convenience of the reader.LetHbe a semialgebraic subgroup ofG.Lemma 2.8 implies thatHis a Nash submanifold ofG.In particular,His locally closed,and thus is an open subgroup of its closureTherefore,His also closed inThis proves this proposition(recall that every closed subgroup of a Lie group is a submanifold). In view of Proposition 3.1,a semialgebraic subgroup of a Nash groupGis also called a Nash subgroup ofG. By Lemma 2.2,we have the following proposition. Proposition 3.2The image of a Nash homomorphism φ:G→G′is a Nash subgroup of G′.In particular,it is closed in G′. It is clear that a Nash subgroup of a Nash group is a Nash group,and the product of two Nash groups is a Nash group.Proposition 2.4 implies that a finite-fold covering group of a Nash group is a Nash group. Proposition 3.3Let G be a topological group,G′be a Nash group,and G→G′be a group homomorphism which is simultaneously a finite-fold topological covering map.Equip on G the Nash structure which makes G→G′a submersive Nash map.Then G becomes a Nash group. ProofUsing Lemma 2.7,this is routine to check. Note that there is no strictly decreasing infinite sequence of Nash subgroups of a Nash group.Consequently,we have the following proposition. Proposition 3.4Let G be a Nash group,andbe a family of Nash subgroups of G.Then for some fi nite subset I0of I.Consequently,the intersection of an arbitrary family of Nash subgroups of G is again a Nash subgroup of G. By a Nash action of a Nash groupGon a Nash manifoldM,we mean a group actionG×M→Mwhich is simultaneously a Nash map.Using Lemma 2.8,we know that eachG-orbit of a Nash actionG×M→Mis a Nash submanifold ofM. The analog of the following proposition for algebraic groups is proved in[3,Chapter I,Proposition 1.8]. Proposition 3.5Let G be a Nash group with a Nash action on a non-empty Nash manifold M.Then each G-orbit in M of the minimal dimension is closed. ProofFor each non-closedG-orbitOinM,there is an orbitO′inO,wheredenotes the closure ofOinM.Then dimO′ A finite-dimensional real representationVof a Nash groupGis called a Nash representation if the action mapG×V→Vis a Nash map.This is equivalent to saying that the corresponding homomorphismG→GL(V)is a Nash homomorphism.Recall from the introduction that a Nash group is said to be almost linear if it has a Nash representation with a finite kernel. In this article,we use a superscript“◦”to indicate the identity connected component of a Nash group. Proposition 3.6A Nash group G is almost linear if and only if is so. ProofThe“only if” part is trivial.Assume thatis almost linear.LetV0be a Nash representation ofwith a finite kernel.Put Under right translations,this is a Nash representation ofGwith a finite kernel. To treat quotient spaces of almost linear Nash groups,recall the following proposition. Proposition 3.7Let G be an almost linear Nash group,and H be a Nash subgroup of it. (1)There exists a Nash representation V of G,and a one-dimensional subspace V1⊂V such that the stabilizer contains H as an open subgroup. (2)If H is normal,then there exists a Nash representation of G whose kernel contains H as an open subgroup. ProofUsing the second assertion of Proposition 2.6,this is an easy consequence of Chevalley’s theorem(see[9,Theorem 11.1.13]). Also recall the following well-known lemma. Lemma 3.1(see[18,Theorem 3.62])Let G×M→M be a transitive smooth action of a Lie group G on a smooth manifold M.Then for each x∈M,the map is a diffeomorphism.Here:={g∈G|g.x=x},and the quotient topological space G/is equipped with the manifold structure so that the quotient map G→G/is smooth and submersive.Consequently,all surjective Lie group homomorphisms are submersive. Here and as usual,all Lie groups and smooth manifolds are assumed to be Hausdorf fand second countable as topological spaces. Proposition 3.8Let G be an almost linear Nash group,and H be a Nash subgroup of it.Then there exists a unique Nash structure on the quotient topological space G/H which makes the quotient map G→G/H a submersive Nash map.With this Nash structure,G/H becomes an affine Nash manifold,and the left translation map G×G/H→G/H is a Nash map.Furthermore,if H is a normal Nash subgroup of G,then the topological group G/H becomes an almost linear Nash group under this Nash structure. ProofUniqueness of such Nash structures is implied by Lemma 2.3.LetVandV1be as in the first assertion of Proposition 3.7.The projective space P(V),which is naturally a Nash manifold,carries the induced Nash action ofG.The image of the map is aG-orbit in P(V),and thus is a Nash submanifold of P(V).It is affine,since P(V)is an affine Nash manifold.Lemma 3.1 implies that the map is a finite-fold topological covering map.Using Proposition 2.4,we equip onG/Hthe Nash structure which makes the map(3.1)a submersive Nash map.Then by Proposition 2.5,G/His an affine Nash manifold,and Lemma 2.7 implies that the left translation mapG×G/H→G/His a Nash map. Now assume thatHis normal.Using the second assertion of Proposition 3.7,we get a Nash homomorphism whose kernel containsHas an open subgroup.Equip onG/Hthe aforementioned Nash structure.Then by Lemmas 2.3 and 3.1,the map(3.2)descends to a submersive Nash map Since(3.3)is a group homomorphism as well as a finite-fold covering map of topological spaces,Proposition 3.3 implies thatG/His a Nash group,which is obviously almost linear. We first observe that every compact subgroup of an almost linear Nash group is a Nash subgroup. Lemma 4.1Let G be an almost linear Nash group,and let K be a compact subgroup of it.Then K is a Nash subgroup of G. ProofFix a Nash homomorphismφ:G→GLn(R)with a finite kernel.Write:=φ(K),which is a compact subgroup of G(R).It is well-known thatis semialgebraic in GLn(R)(it is actually Zariski closed in G(R)(see[6,Lemma 3.3.1])).Note thatis a Nash subgroup ofG,and has the same dimension as that ofK.Therefore,Kis an open subgroup of(,and thus is semialgebraic inG. Recall from Section 1 that an elliptic Nash group is defined to be an almost linear Nash group which is compact as a topological space. Lemma 4.2Let G be an almost linear Nash group,and K be an elliptic Nash group.Then every Lie group homomorphism φ:K→G is a Nash homomorphism.In particular,every fi nite-dimensional real representation of K is a Nash representation. ProofThe graph ofφis a compact subgroup of the almost linear Nash groupK×G.Therefore,it is semialgebraic by Lemma 4.1. Lemma 4.3Let K be a compact Lie group.Then there is a unique Nash structure on the underlying topological space of K which makes K an almost linear Nash group. ProofUniqueness follows from Lemma 4.2.To prove the existence,fix an injective Lie group homomorphismφ:KGLn(R)(such a homomorphism always exists,see[6,Section 3.3.C]).By Lemma 4.1,φ(K)is a Nash group.The existence then follows by transferring the Nash structure onφ(K)toK,through the topological group isomorphismφ:Kφ(K). Combining Lemmas 4.1–4.3,we get Theorem 1.1.Moreover,we have proved the following theorem. Theorem 4.1The category of elliptic Nash groups is isomorphic to the category of compact Lie groups. The following proposition is obvious. Proposition 4.1All Nash subgroups and Nash quotient groups of all elliptic Nash groups are elliptic as Nash groups. Recall that a linear operatorxon a finite-dimensional vector spaceVis said to be semisimple if everyx-stable subspace ofVhas a complementaryx-stable subspace.IfVis defined over a field k of characteristic zero,then for each field extensionof k,xis semisimple if and only if thelinear operator is semisimple.IfVis defined over an algebraically closed field,thenxis semisimple if and only if it is diagonalizable. The following result concerning representations of compact Lie groups is well-known.We provide a proof for completeness. Proposition 4.2Let V be a Nash representation of an elliptic Nash group G.Then each element of G acts as a semisimple linear operator on V,and all its eigenvalues are complex numbers of modulus1. ProofSince every element ofGis contained in a compact abelian subgroup ofG,we assume without loss of generality thatGis abelian.Then the complexificationVCofVis a direct sum of one-dimensional subrepresentations.By choosing an appropriate basis ofVC,the representation corresponds to a Nash homomorphism Compactness ofGimplies that the image of(4.1)is contained in Sn(recall from the Introduction that S denotes the Nash group of complex numbers of modulus one).This proves this proposition. The following important result is due to Cartan,Malcev and Iwasawa.For a proof,see[4,Theorem 1.2]for example. Theorem 4.2Let G be a Lie group with finitely many connected components.Then every compact subgroup of G is contained in a maximal one,and all maximal compact subgroups of G are conjugate to each other.Moreover,for each maximal compact subgroup K of G,there exists a closed submanifold X of G which is diffeomorhpic tosuch that the multiplication map K×X→G is a diffeomorphism. We say that a Nash group is unipotent if it has a faithful Nash representation so that all group elements act as unipotent linear operators.It is obvious that each Nash subgroup of a unipotent Nash group is a unipotent Nash group. First recall the following well-known result,which is basic to the study of unipotent Nash groups. Lemma 5.1(see[8])For each connected,simply connected,nilpotent Lie group N,the exponential map is a diffeomorphism. Here and henceforth,“Lie” indicates the Lie algebra of a Lie group. Recall from Section 1 that a subgroup of a Lie groupGis said to be analytic if it equals the image of an injective Lie group homomorphism from a connected Lie group toG.Every analytic subgroup is canonically a connected Lie group.We remark that in general,the topology on a non-closed analytic subgroup does not coincide with the subspace topology.The set of all analytic subgroups ofGis in one-to-one correspondence with the set of all Lie subalgebras of LieG. Lemma 5.2Let N be a connected,simply connected,nilpotent Lie group.Then each analytic subgroup of N is closed in N,and is a connected,simply connected,nilpotent Lie group. ProofLet n0be a Lie subalgebra of LieN.LetN0be a connected,simply connected Lie group with Lie algebra n0.ThenN0is nilpotent,and there is a commutative diagram whereφis the Lie group homomorphism whose differential is the inclusion map n0LieN.By Lemma 5.1,the two vertical arrows are diffeomorphisms.Since the top horizontal arrow is a closed embedding,φis also a closed embedding.Then this lemma follows,sinceφ(N0)is the analytic subgroup ofNcorresponding to n0. Lemma 5.3Let V be a finite-dimensional real representation of a connected Lie group G.If all elements of G act as unipotent linear operators on V,then G kills a full flag of V,namely,there exists a sequence of subspaces of V,such thatdimVi=i(i=0,1,2,···,n),and ProofTaking the differential of the representation,LieGacts as nilpotent linear operators onV.Therefore,this lemma is a direct consequence of Engel’s theorem. Now we come to the study of unipotent Nash groups. Lemma 5.4Every unipotent Nash group is connected. ProofProposition 4.2 implies that a maximal compact subgroup of a unipotent Nash group is trivial.Therefore,this lemma follows by Theorem 4.2. Denote by Un(R)(n≥0)the subgroup of GLn(R)consisting all unipotent upper-triangular matrices.This is a unipotent Nash group.As a Lie group,it is connected,simply connected,and nilpotent.The Lie algebra un(R)of Un(R)consists all nilpotent upper-triangular matrices in gln(R). Lemma 5.5Every unipotent Nash group is Nash isomorphic to a Nash subgroup ofUn(R)for some n≥0. ProofThis is a direct consequence of Lemmas 5.3–5.4. Proposition 5.1Every unipotent Nash group is connected,simply connected and nilpotent. ProofThis is implied by Lemmas 5.2 and 5.4–5.5. Proposition 5.2For each unipotent Nash group N,the exponential map is a Nash diffeomorphism. ProofProposition 5.1 and Lemma 5.1 imply that(5.1)is a diffeomorphism.Using Lemma 5.5,we fix an injective Nash homomorphismφ:N→Un(R).Then we have a commutative diagram whereϕdenotes the differential ofφ.Note that in the above diagram,the right vertical arrow is a Nash diffeomorphism,and the two horizontal arrows are Nash embeddings.Therefore,the left vertical arrow is a Nash diffeomorphism. Proposition 5.3Every analytic subgroup of a unipotent Nash group is a Nash subgroup. ProofLetN0be an analytic subgroup of a unipotent Nash groupN.Then we have acommutative diagram By Proposition 5.2,the right vertical arrow of(5.2)is a Nash diffeomorphism.By Lemmas 5.1–5.2,the left vertical arrow of(5.2)is a diffeomorphism.Therefore,N0is semialgebraic inN,since LieN0is semialgebraic in LieN. Proposition 5.4Let N,N′be two unipotent Nash groups.Then every Lie group homomorphism φ:N→N′is a Nash homomorphism. ProofIt easily follows from Proposition 5.2. Proposition 5.5Let N be a connected,simply connected,nilpotent Lie group.Then there exists a unique Nash structure on the underlying topological space of N which makes N a unipotent Nash group. ProofThe uniqueness assertion follows from Proposition 5.4.To prove the existence,it suffices to show that there exists a unipotent Nash group which is isomorphic toNas a Lie group.Since all unipotent Nash groups are connected and simply connected(see Proposition 5.1),it suffices to show that there exists a unipotent Nash group whose Lie algebra is isomorphic to LieN. As a special case of Ado’s theorem,LieNis isomorphic to a Lie subalgebra of un(R)for somen≥0(see[14,Theorem 7.19]).Identify LieNwith a Lie subalgebra of un(R).By Proposition 5.3,the corresponding analytic subgroup of Un(R)is a unipotent Nash group.Therefore,this proposition follows. Combining Propositions 5.1 and 5.3–5.5,we get Theorem 1.2.We have also proved the following theorem. Theorem 5.1The category of unipotent almost linear Nash groups is isomorphic to the category of connected,simply connected,nilpotent Lie groups. The following lemma will be used later. Lemma 5.6Let N be a connected Nash group.If N has a Nash representation with a finite kernel so that all group elements act as unipotent linear operators,then N is unipotent. ProofUsing Lemma 5.3,we get a Nash homomorphismφ:N→Un(R)with finite kernel.By Proposition 5.1,φ(N)is connected and simply connected.This implies thatφ:N→φ(N)is a Nash isomorphism,and this lemma follows. The groupof positive real numbers is an almost linear Nash group in the obvious way.We define a hyperbolic Nash group to be a Nash group which is Nash isomorphic to()nfor somen≥0. As in Section 1,for every two Nash groupsGandG′,write Hom(G,G′)for the set of all Nash homomorphisms fromGto.It is obviously an abelian group whenG′is abelian,and is a ring whenG=andis abelian. We leave the proof of the following lemma to the interested reader. Lemma 6.1The map is a ring isomorphism. Using the isomorphism(6.1),we viewas a right Q-vector space as in Section 1.Then for every hyperbolic Nash groupA,the abelian group Hom(A)is a left Q-vector space: where(denotes the endomorphismx 7→of.By Lemma 6.1,the dimension of Hom(,A)equals that ofA. On the other hand,given a Q-vector spaceEof finite dimensionk,the tensor product is obviously a hyperbolic Nash group of dimensionk. Proof of Theorem 1.3This is an obvious consequence of Lemma 6.1. Moreover,we have the following proposition. Proposition 6.1Every Nash subgroup of a hyperbolic Nash group is a hyperbolic Nash group. ProofLetHbe a Nash subgroup ofA1×A2×···×Ak,wherek≥0,and eachAiis a Nash group which is Nash isomorphic to(i=1,2,···,k).We want to show thatHis a hyperbolic Nash group.Assume without loss of generality thatHA.ThenAiis not contained inHfor somei.ThenAi∩H={1},and we get an injective Nash homomorphismHA/Ai.The lemma then follows by an inductive argument. Similarly,we have the following proposition. Proposition 6.2Every Nash quotient group of a hyperbolic Nash group is a hyperbolic Nash group. ProofLetA0be a Nash subgroup of a hyperbolic Nash groupA.By Proposition 6.1,A0is also a hyperbolic Nash group.Using Theorem 1.3,we get an exact sequence of left Q-vector spaces.Tensoring with,we get an exact sequence of hyperbolic Nash groups and Nash homomorphisms.Therefore,the proposition follows. First recall the following well-known fact. Lemma 7.1The hyperbolic Nash groupis not Nash isomorphic to the unipotent Nash groupR. ProofNote that the Nash endomorphism ring Hom(R,R)is isomorphic to R.By Lemma 6.1,the Nash endomorphism ring Hom(,)is isomorphic to Q.Therefore,this lemma holds. The following is a useful fact about unipotent Nash groups. Lemma 7.2Every non-trivial element of a unipotent Nash group is contained in a Nash subgroup which is Nash isomorphic toR. ProofThis is directly implied by Proposition 5.2. Elliptic Nash groups,hyperbolic Nash groups and unipotent Nash groups are disjoint to each other in the following sense. Proposition 7.1Let G and G′be two Nash groups.If G is elliptic,and G′is hyperbolic or unipotent,then The same holds if G is hyperbolic,and G′is elliptic or unipotent;or if G is unipotent,and G′is elliptic or hyperbolic. ProofNote that all hyperbolic Nash groups and all unipotent Nash groups have no nontrivial compact subgroups.Therefore,Hom(G,G′)={1}ifGis elliptic,andG′is hyperbolic or unipotent. Note that ifG′is elliptic,then The first equality of(7.1)implies that Hom(G,G′)={1},ifGis hyperbolic andG′is elliptic.By Lemma 7.2,the second equality of(7.1)implies that Hom(G,G′)={1},ifGis unipotent andG′is elliptic. Lemma 7.1 implies that ifG′is unipotent.Therefore,Hom(G,G′)={1},ifGis hyperbolic andG′is unipotent.Lemma 7.1 also implies that ifG′is hyperbolic.By Lemma 7.2,(7.2)implies that Hom(G,G′)={1},ifGis unipotent andG′is hyperbolic.This finishes the proof of this proposition. Proposition 7.2Let H1,H2,H3be three Nash subgroups of a Nash group G.If they are respectively elliptic,hyperbolic and unipotent,then they have pairwise trivial intersections. ProofThe Nash groupH1∩H2is elliptic and hyperbolic,and is hence trivial by Proposition 7.1.Similarly,H1∩H3andH2∩H3are trivial. Lemma 7.3Let G1be an elliptic Nash group,and let G2be a hyperbolic Nash group.Then all Nash subgroups of G1×G2are of the form H1×H2,where Hiis a Nash subgroup of Gi,i=1,2. ProofLetHbe a Nash subgroup ofG1×G2.We first claim that Consider the restriction toHof the projection map The conditionH∩G2={1}implies thatHis an elliptic Nash group.Then by Proposition 7.1,the projection map has trivial restriction toH.Therefore,H⊂G1,and the claim is proved. In general,put=G2/(G2∩H),which is a hyperbolic Nash group.WriteH′for the image ofHunder the Nash homomorphism Inside the groupG1×we have and then(7.3)implies This lemma then follows asH= Lemma 7.4Let G1be the direct product of an elliptic Nash group and a hyperbolic Nash group,and let G2be a unipotent Nash group.Then all Nash subgroups of G1×G2are of the form H1×H2,where Hiis a Nash subgroup of Gi,i=1,2. ProofLemma 7.3 and its proof show Lemma 7.4 whenG2is abelian.In general,letHbe a Nash subgroup ofG1×G2,and letxy∈H,wherex∈G1andy∈G2.It suffices to show thaty∈G2.ReplacingG2by an abelian Nash subgroupofGcontainingy,and replacingHbyH∩(G1×),this lemma is reduced to the case whenG2is abelian. Combining Lemmas 7.3–7.4,we get the following proposition. Proposition 7.3Let G1,G2,G3be three Nash groups which are respectively elliptic,hyperbolic and unipotent.Then every Nash subgroup of G1×G2×G3is of the form H1×H2×H3,where Hiis a Nash subgroup of Gi,i=1,2,3. As a direct consequence of Proposition 7.3,we have the following proposition. Proposition 7.4Let H1,H2,H3be three Nash subgroups of a Nash group G which are respectively elliptic,hyperbolic and unipotent.If they pairwise commute with each other,then the multiplication map H1×H2×H3→G is an injective Nash homomorphism. In the rest of this section,we draw some consequences of Proposition 7.1 on unipotent Nash groups and hyperbolic Nash groups. Proposition 7.5Let V be a Nash representation of a unipotent Nash group G.Then each element of G acts as a unipotent linear operator on V. ProofUsing Lemma 7.2,we assume without loss of generality thatG=R.LetV1be an irreducible subquotient representatoin of the complexificationVCofV.SinceGis abelian,it is one-dimensional and corresponds to a Nash homomorphism This homomorphism is trivial by Proposition 7.1.Therefore,this proposition follows. As a consequence of Proposition 7.5,we have the following proposition. Proposition 7.6Every Nash quotient group of a unipotent Nash group is unipotent. ProofLetNbe a unipotent Nash group,andN′be a Nash quotient group of it.Fix a Nash representationVofN′with finite kernel.Applying Proposition 7.5 to the inflation of the representationVtoN,we know thatN′acts onVas unipotent linear operators.Then this proposition follows by Lemma 5.6. Proposition 7.7All irreducible Nash representations of all unipotent Nash groups are trivial. ProofThis is implied by Proposition 7.5 and Lemma 5.3. Now we consider Nash representations of hyperbolic Nash groups. Lemma 7.5Let V be a Nash representation of a hyperbolic Nash group G.If each element of G acts as a unipotent linear operator on V,then the representation V is trivial. ProofBy Lemma 5.3,the image of the attached homomorphismG→GL(V)is contained in a unipotent Nash subgroup of GL(V).Therefore,the homomorphism is trivial by Proposition 7.1. Proposition 7.8Let V be a Nash representation of a hyperbolic Nash group G.Then each element of G acts as a semisimple linear operator on V,and all its eigenvalues are positive real numbers. ProofBy Proposition 7.1,the image of every Nash homomorphism fromGto C×is contained in.This implies that for everyg∈G,all eigenvalues ofφ(g)are positive real numbers,whereφ:G→GL(V)denotes the Nash homomorphism attached to the representation.Using the generalized eigenspace decomposition,we assume without loss of generality that there is a Nash homomorphismχ:G→such that for everyg∈G,all eigenvalues ofφ(g)are equal toχ(g).ThenGacts onV⊗by unipotent linear operators.This action is trivial by Lemma 7.5.Therefore,Gacts onVvia the characterχ,and this proposition is proved. Proposition 7.8 clearly implies the following result. Proposition 7.9Every Nash representation of a hyperbolic Nash group is a direct sum of one-dimensional subrepresentations. LetGbe an almost linear Nash group throughout this section.For everyx∈G,define its replicato be the smallest Nash subgroup ofGcontainingx.This is well-defined by Proposition 3.4.It is easy to see thatis abelian. We say thatx∈Gis elliptic,hyperbolic or unipotent if it is contained in a Nash subgroup ofGwhich is elliptic,hyperbolic or unipotent,respectively.This is equivalent to saying that the abelian Nash groupis respectively elliptic,hyperbolic or unipotent.Respectively writeGe,GhandGufor the sets of all elliptic,hyperbolic and unipotent elements inG. Lemma 8.1An element inGLn(R)(n≥0)is elliptic if and only if it is semisimple and all its eigenvalues are complex numbers of modulus one;it is hyperbolic if and only if it is semisimple and all its eigenvalues are positive real numbers;it is unipotent if and only if all its eigenvalues are equal to1. ProofThe“if” parts of the three assertions of this lemma are obvious.The“only if” parts are implied by Propositions 4.2,7.5 and 7.8. Lemma 8.2Let e,h,u∈G.Assume that they are respectively elliptic,hyperbolic and unipotent,and they pairwise commute with each other.Then and the multiplication map is an isomorphism of Nash groups. ProofFirst note that the subgroupsare pairwise commutative to each other.Using Proposition 7.4,we viewas a Nash subgroupG.Thenis a Nash subgroup ofand Proposition 7.3 implies that This proves this lemma. Here is the Jordan decomposition theorem for almost linear Nash groups as follows. Theorem 8.1Every element x of an almost linear Nash group G is uniquely of the form x=ehu such that e∈Ge,h∈Gh,u∈Gu,and they pairwise commute with each other. ProofFix a Nash homomorphismφ:G→GLn(R)with a finite kernel.Puty:=φ(x)and writey=for the usual Jordan decomposition ofyin GLn(R),whereis elliptic,yhis hyperbolic,yuis unipotent and they pairwise commute with each other(see[10,pp.430–431]).Then Lemma 8.2 implies Denote byhthe unique element in the identity connected component ofwhich liftsyh.Defineusimilarly,and pute:=Then it is routine to check that(e,h,u)is the unique triple which fulfills all the requirements of the theorem. The equalityx=ehuof Theorem 8.1 is called the Jordan decomposition ofx∈G.We respectively usexhandxuto denote the elementse,handu.They are respectively called the elliptic,hyperbolic and unipotent parts ofx∈G. Proposition 8.1Let φ:G→G′be a Nash homomorphism of almost linear Nash groups.Then If φ is surjective,then the three inclusions in(8.1)become equalities. ProofThe three inclusions are respectively implied by Propositions 4.1,6.2 and 7.6. Now assume thatφis surjective,and lety∈Pickx∈Gso thatφ(x)=y.Then=y.By(8.1),the uniqueness of Jordan decompositions implies thatφ(=y.This proves thatφ()=.The same argument proves the other two equalities. Proposition 8.1 obviously implies that Nash homomorphisms preserve Jordan decompositions: Proposition 8.2Let φ:G→G′be a Nash homomorphism of almost linear Nash groups.Then for every x∈G,one has As one application of Jordan decompositions,we get the following result about structures of abelian almost linear Nash groups. Proposition 8.3Let G be an abelian almost linear Nash group.Then Geis an elliptic Nash subgroup of G,Ghis a hyperbolic Nash subgroup of G,and Guis a unipotent Nash subgroup of G.Moreover,the multiplication map is a Nash isomorphism. ProofLetKbe a maximal compact subgroup ofG,which is unique sinceGis abelian.Then clearlyK=LetAbe a hyperbolic Nash subgroup ofGof the maximal dimension.Then clearlyA=Gh.Likewise,letUbe a unipotent Nash subgroup ofGof the maximal dimension.ThenU=Gu.The last assertion follows from Theorem 8.1. In the rest of this section,denote by g the Lie algebra of the almost linear Nash groupG.For everyx∈g,we define its replicato be the smallest Nash subgroup ofGcontaining exp(Rx).It is connected and abelian.We said thatx∈g is elliptic,hyperbolic or unipotent,if the Nash group⟩is respectively elliptic,hyperbolic or unipotent.As in the group case,respectively write ge,ghand gufor the sets of all elliptic,hyperbolic and unipotent elements in g. Lemma 8.1 easily implies the following lemma. Lemma 8.3An element in the Lie algebragln(R)ofGLn(R)(n≥0)is elliptic if and only if it is semisimple and all its eigenvalues are purely imaginary;it is hyperbolic if and only if it is semisimple and all its eigenvalues are real;it is unipotent if and only if it is a nilpotent matrix. The same proof as Lemma 8.2 shows the following lemma. Lemma 8.4Let e,h,u∈g.Assume that they are respectively elliptic,hyperbolic and unipotent,and they pairwise commute with each other.Then and the multiplication map is an isomorphism of Nash groups. The following is the Jordan decomposition theorem at the Lie algebra level. Theorem 8.2Let G be an almost linear Nash group with Lie algebrag.Then every element x∈gis uniquely of the form x=e+h+u such that eand they pairwise commute with each other. ProofThe proof is similar to that of Theorem 8.1.We omit the details. We also call the equalityx=e+h+uof Theorem 8.2 the Jordan decomposition ofx∈g.As in the group case,we respectively usexe,xhandxuto denote the elementse,handu.They are respectively called the elliptic,hyperbolic and unipotent parts ofx∈g. The same proof as Proposition 8.1 shows the following proposition. Proposition 8.4Let φ:G→G′be a Nash homomorphism of almost linear Nash groups.Write ϕ:g→g′for its differential,whereg′:=LieG′.Then If ϕ is surjective,then the three inclusions in(8.2)become equalities. Similar to Proposition 8.2,the above proposition implies the following proposition. Proposition 8.5Let φ:G→G′be a Nash homomorphism of almost linear Nash groups.Write ϕ:g→g′for its differential,whereg′:=LieG′.Then for every x∈g,one has LetGbe an almost linear Nash group with Lie algebra g.The following lemma concerning the exponential map is obvious. Lemma 9.1One has For eachx∈or,define log(x)to be the unique element in the Lie algebra of⟨x⟩such that exp(log(x))=x.Then log(x)belongs toor,respectively.The maps are inverse to each other.Likewise,the maps are inverse to each other. Lemma 9.2Let x∈or.Then ProofThe Nash subgroupofGcontains the Nash subgroupSincex∈Lieand exp(x)∈using the commutative diagram we know thatx∈LieTherefore, and hence Lemma 9.3Let x∈Ghand y∈Gu.If they commute with each other in G,thenlog(x)andlog(y)commute with each other ing. ProofIfxandycommute with each other,then Lemma 9.2 implies that the Nash subgroupscommute with each other.Therefore,is an abelian Nash subgroup ofG.Then this lemma follows,since both log(x)and log(y)belong to the Lie algebra of Definition 9.1An element of an almost linear Nash group G or its Lie algebragis said to be exponential if its elliptic part is trivial. Denote byandthe sets of all exponential elements inGand g,respectively.For every exponential elementx∈,define By Lemma 9.3,this is an element of Proposition 9.1The maps are inverse to each other. ProofThis is obvious. Proposition 9.2Let x∈. ProofBy Lemmas 9.2,8.2 and 8.4,we have We say that a Lie group(or a Nash group)is semisimple if its Lie algebra is semisimple. Lemma 10.1Every semisimple Nash group is almost linear. ProofTaking the adjoint representation,then this lemma follows. Recall the following result. Lemma 10.2(see[12,Proposition 7.9])Every semisimple analytic subgroup ofGLn(R)(n≥0)has a finite center. Using Cartan decompositions for semisimple Lie groups(see[12,Theorem 7.39]),we easily get the following result. Lemma 10.3Let G be a connected semisimple Lie group with a finite center.Let K be a maximal compact subgroup of G.Then there are analytic subgroups ,,···,Hr(r≥0)of G such that (1)G=KH1H2···HrK, (2)the Lie algebra of Hiis isomorphic to(R)(i=1,2,···,r). Recall that every analytic subgroup ofis isomorphic to either SL2(R)or SL2(R)/{±1},if its Lie algebra is isomorphic toThe representation theory of SL2(R)implies the following lemma. Lemma 10.4Every finite-dimensional real representation ofis a Nash representation. As a direct consequence of Lemma 10.4,we have the following lemma. Lemma 10.5An analytic subgroup ofGLn(R)is a Nash subgroup if its Lie algebra is isomorphic tosl2(R). Combining Lemmas 4.1,10.2,10.3 and 10.5,we have the following lemma. Lemma 10.6Every semisimple analytic subgroup ofGLn(R)(n≥0)is a Nash subgroup. By Lemma 10.6,the same proof as that of Lemma 4.1 implies the following proposition. Proposition 10.1Every semisimple analytic subgroup of every almost linear Nash group is a Nash subgroup. In a way similar to the proof of Lemma 4.2,Proposition 10.1 implies the following proposition. Proposition 10.2Every Lie group homomorphism from a semisimple Nash group to an almost linear Nash group is a Nash homomorphism.In particular,every finite-dimensional representation of a semisimple Nash group is a Nash representation. Each semisimple Nash group has finitely many connected components,and its identity connected component has a finite center.Conversely,we have the following proposition. Proposition 10.3Let G be a semisimple Lie group.If it has finitely many connected components,and its identity connected component has a finite center,then there exists a unique Nash structure on the underlying topological space of G which makes G a Nash group. ProofDenote by g the Lie algebra ofG.The automorphism group Aut(g)of g is obviously a Nash group.The adjoint representation Ad:G→Aut(g)has an open image and a finite kernel.Therefore,the existence follows by Proposition 3.3.The uniqueness is implied by Proposition 10.2. In conclusion,we have proved the following theorem. Theorem 10.1The category of semisimple Nash groups is isomorphic to the category of semisimple Lie groups which have finitely many connected components,and whose identity connected components have finite centers. Recall the following famous result of Weyl. Lemma 10.7(see[11,Theorem 1])Letgbe a semisimple finite-dimensional Lie algebra over a fieldkof characteristic zero.Then all of its finite-dimensional representations overkare completely reducible. Also recall the following elementary lemma. Lemma 10.8(see[15,Lemma 3.1])Let H be a normal subgroup of a group G.Let V be a representation of G over a fieldk. (1)If V is finite-dimensional and completely reducible,then its restriction to H is completely reducible. (2)Assume that H has finite index in G,and k has characteristic zero.Then V is completely reducible if its restriction to H is so. Combining Lemma 10.7 and Lemma 10.8(2),we get the following lemma. Lemma 10.9Every Nash representation of a semisimple Nash group is completely reducible. We say that a Nash group is reductive if it has a completely reducible Nash representation with a finite kernel.Using induced representations as in the proof of Proposition 3.6,Lemma 10.8 easily implies the following lemma. Lemma 11.1A Nash group is reductive if and only if its identity connected component is reductive. Recall from Introduction that a Nash torus is a Nash group which is Nash isomorphic tofor somem,n≥0.Every Nash torus is clearly a reductive Nash group.The main result we will prove in this section is the following theorem. Theorem 11.1A connected Nash group G is reductive if and only if there exists a connected semisimple Nash group H,a Nash torus T,and a surjective Nash homomorphism H×T→G with a finite kernel. Recall that a finite-dimensional Lie algebra is said to be reductive if its adjoint representation is completely reducible,or equivalently,if it is the direct sum of an abelian Lie algebra and a semisimple Lie algebra.Recall the following result of Jacobson. Lemma 11.2([11,Theorem 1])Letgbe a finite-dimensional Lie algebra over a fieldkof characteristic zero.Ifghas a faithful completely reducible finite-dimensional representation overk,thengis reductive. Combining Lemmas 11.1–11.2,we get the following lemma. Lemma 11.3The Lie algebra of every reductive almost linear Nash group is reductive. LetGbe a connected reductive Nash group with Lie algebra g.Write where s:=[g,g]and z denotes the center of g.Respectively writeSandZfor the analytic subgroups ofGcorresponding to s and z.By Proposition 10.1,Sis a Nash subgroup ofG.SinceZequals the identity connected component of the center ofG,it is also a Nash subgroup ofG. Lemma 11.4The Nash group Z is a Nash torus. ProofNote thatZis a normal subgroup ofG.The first assertion of Lemma 10.8 implies thatZis reductive.Similarly,Zuis reductive(Proposition 8.3 implies thatZuis a unipotent Nash group).Then Proposition 7.7 implies thatZu={1},and henceZis a Nash torus by Proposition 8.3. SinceS×Zis a finite-fold cover ofG,we prove the“only if”part of Theorem 11.1. On the other hand,letG′be a connected Nash group with a surjective Nash group homomorphismH×T→G′with a finite kernel,whereHis a connected semisimple Nash group,andTis a Nash torus.ThenG′is almost linear by Proposition 3.8. Lemma 11.5Every Nash representation of a Nash torus is completely reducible. ProofBy Weyl’s unitary trick,every Nash representation of an elliptic Nash group is completely reducible.In particular,every Nash representation of a compact Nash torus is completely reducible.Together with Proposition 7.9,this implies this lemma. By Lemmas 11.5 and 10.9,every Nash representation ofH×Tis completely reducible.Consequently,every Nash representation ofG′is also completely reducible.Therefore,G′is reductive.This proves the “if part” of Theorem 11.1. By Lemma 10.8,the preceding arguments also show the following theorem. Theorem 11.2Every Nash representation of every reductive almost linear Nash group is completely reducible. LetGbe an almost linear Nash group with Lie algebra g.Fix a Nash representationVofGwith a finite kernel,and writeϕ:g→gl(V)for the attached differential.Put This defines aG-invariant symmetric bilinear form on g,which is called the trace form attached to the Nash representationV. The main result of this section is the following theorem. Theorem 12.1The almost linear Nash group G is reductive if and only if the bilinear formis non-degenerate. Theorem 12.1 has the following interesting consequence. Proposition 12.1Assume that G is reductive.Then for every reductive Nash subgroup H1of G,its centralizer H2in G is also a reductive Nash subgroup of G. ProofBy Theorem 12.1,is a non-degenerate symmetric bilinear form on g.It isG-invariant,and henceH1-invariant.SinceH1is reductive,by Theorem 11.2,g is completely reducible as a representation ofH1.Taking the isotypic decomposition,we know that the spaceofH1-fixed vectors in g is non-degenerate with respect to.Sinceequals the Lie algebra ofH2,this proposition follows by Theorem 12.1. The rest of this section is devoted to a proof of Theorem 12.1. Lemma 12.1If G is elliptic,then the bilinear formis negative definite.If G is hyperbolic,then the bilinear formis positive definite. ProofThis is implied by Lemma 8.3. Lemma 12.2Let x and y be two commuting elements in the Lie algebragl(V)ofGL(V).If x is elliptic and y is hyperbolic,thentr(xy)=0. ProofNote that all eigenvalues ofxare purely imaginary,and all eigenvalues ofyare real.Sincexandycommute,all eigenvalues ofxyare purely imaginary.Therefore,tr(xy)is purely imaginary.It has to vanish since it is also real. Lemma 12.3If G is a Nash torus,then the bilinear formis non-degenerate. ProofWriteG=T×A,whereTis a compact Nash torus,andAis a hyperbolic Nash group.Lemma 12.2 implies that LieTand LieAare orthogonal to each other under the symmetric bilinear formThe lemma then follows by Lemma 12.1. Lemma 12.4If G is a connected semisimple Nash group andis zero,then G is trivial. ProofLetKbe a maximal compact subgroup ofG,which is connected sinceGis connected.Then Lemma 12.1 implies thatKis trivial,which further implies thatGis trivial(recall thatevery non-trivial connected semisimple Lie group with a finite center has a non-trivial maximal compact subgroup). We are now prepared to prove the “only if”part of Theorem 12.1. Proposition 12.2If G is reductive,then the bilinear formis non-degenerate. ProofDenote by n the kernel of the form.It is an ideal of the reductive Lie algebra g.Lemma 12.3 implies that n⊂[g,g].Therefore,n is semisimple.Denote byNthe analytic subgroup ofGwith Lie algebra n.It is a connected semisimple Nash subgroup ofGby Proposition 10.1.Then Lemma 12.4 implies thatNis trivial,and hence n={0}. To prove the “if” part of Theorem 12.1,recall the following lemma. Lemma 12.5(see[5,Lemma 3.1 and Proposition 3.2])Let V0be a finite-dimensional vector space over a field of characteristic zero.Letg0be a Lie subalgebra ofgl(V0)such that the trace form is non-degenerate ong0.Theng0is reductive,and no non-zero element in the center ofg0is nilpotent as a linear operator on V0. Now assume thatis non-degenerate.We want to show thatGis reductive.In view of Lemma 11.1,we may(and do)assume thatGis connected. Lemma 12.5 implies that the Lie algebra g is reductive.Write where z denotes the center of g,and s:=[g,g].Denote byZandSthe analytic subgroups ofGrespectively corresponding to z and s.As before,bothZandSare Nash subgroups ofG.Using Proposition 8.3,writeZ=Ze×Zh×Zu.Then Lemma 12.5 implies thatZu={1}.Therefore,Zis a Nash torus.SinceZ×Sis a finite-fold cover ofG,Gis reductive by Theorem 11.1.This proves the “if” part of Theorem 12.1. LetGbe an almost linear Nash group with Lie algebra g. Definition 13.1An element of G orgis said to be semisimple if its unipotent part is trivial. We define a Nash quasi-torus to be an abelian almost linear Nash group without non-trivial unipotent element.All Nash quasi-tori are reductive Nash groups.First,we have the following lemma. Lemma 13.1An element x∈G is semisimple if and only ifis a Nash quasi-torus.An element y∈gis semisimple if and only ifis a Nash torus. ProofThe “if” part of the first assertion is obvious.To prove the “only if” part of the first assertion,assume thatxis semisimple.Then⟩by Lemma 8.2.Therefore,⟩is a Nash quasi-torus.The proof of the second assertion is similar. Writefor the sets of all semisimple elements inGand g,respectively. Lemma 13.2Let φ:G→G′be a Nash homomorphism of almost linear Nash groups.Then and the inclusion becomes an equality if φ is surjective.Write ϕ:g→g′for the differential of φ,whereg′denotes the Lie algebra of G′.Then and the inclusion becomes an equality if ϕ is surjective. ProofThe proof is similar to that of Proposition 8.1. The rest of this section is to prove the following theorem. Theorem 13.1If G is reductive,then the setis dense in G,and the setis dense ing. We begin with the following lemma. Lemma 13.3If G is connected andgis isomorphic to(R),then is dense in G. ProofIt is elementary to check that this lemma holds whenG=SL2(R),which implies that this lemma also holds whenG=R)/{±1}.In general,there is a surjective Nash homomorphismφ:G→SL2(R)/{±1}with a finite kernel.The lemma then follows,since Lemma 13.4Let u be a unipotent element of a reductive Nash group G.Then every neighborhood of u in G contains a semisimple element. ProofThe lemma is trivial whenu=1.So assume thatu1.Since every element of the center of g is semisimple,log(u)belongs to the semisimple Lie algebra[g,g].Since log(u)is unipotent,the linear operator is nilpotent.Therefore,by the Jacobson-Morozov theorem,there is a Lie subalgebra g0of g containing log(u)which is isomorphic to sl2(R).Denote byG0the analytic subgroup ofGwith Lie algebra g0.It is a Nash subgroup by Proposition 10.1.The lemma then follows by Lemma 13.3. We are now ready to prove Theorem 13.1.Letxbe an element of a reductive Nash groupG.The centralizerinGequals the centralizer of the Nash quasi-torus⟩inG.Therefore,it is a reductive Nash subgroup ofGby Proposition 12.1.Note that the product of two commuting semisimple elements in an almost linear Nash group is again semisimple.By Lemma 13.4,every neighborhood ofcontains a semisimple element.Therefore,every neighborhood ofx=inGcontains a semisimple element.This finishes the proof of Theorem 13.1 in the group case.The Lie algebra case is proved similarly. LetGbe an almost linear Nash group.Put whereπruns through all irreducible Nash representations ofG.By Proposition 3.4,UGis a Nash subgroup ofG. Proposition 14.1The groupis the largest normal unipotent Nash subgroup of G. ProofIt is obvious thatis a normal subgroup ofG.Take a Nash representationVofGwith a finite kernel.Note thatacts trivially on all irreducible Nash representations ofG.Therefore,by taking a Jordan-Hölder series ofV,we know thatacts onVas unipotent linear operators.Then Lemma 5.6 implies thatis a unipotent Nash group. LetUbe a normal unipotent Nash subgroup ofG.It is connected by Proposition 5.1.For every irreducible Nash representationπofG,the restrictionis completely reducible by the first assertion of Lemma 10.8.SinceUis unipotent,Proposition 7.7 implies thatUacts trivially onπ.This shows thatU⊂ We call UGthe unipotent radical ofG. Lemma 14.1An almost linear Nash group is reductive if and only if its unipotent radical is trivial. ProofThe“only if” part of the lemma is obvious.The“if” part is implied by Proposition 3.4. Proposition 3.4 also implies thatG/is a reductive Nash group. Theorem 14.1Every reductive Nash subgroup of G is contained in a maximal one,and all maximal reductive Nash subgroups of G are conjugate to each other underUG.Moreover,for each maximal reductive Nash subgroup L of G,one has that G=LUG. The equalityG=LUGof Theorem 14.1 is called a Levi decomposition ofG,and a maximal reductive Nash subgroup ofGis called a Levi component ofG. The rest of this section is devoted to a proof of Theorem 14.1.We fist recall some results of G.D.Mostow on linear Lie algebras. For a finite-dimensional Lie algebra g over a field of characteristic zero,write Rad(g)for its radical,namely,the largest solvable ideal of g.For a Lie subalgebra h of g,we define Ig(h)to be the subgroup of the automorphism group Aut(g)generated by the set Given a finite-dimensional vector spaceV,we say that a subsetR⊂gl(V)is fully reducible if eachR-stable subspace ofVhas a complementaryR-stable subspace.This generalizes the notion of“semisimple linear operators”. Lemma 14.2(see[15,Theorems 4.1 and 5.1])Let V be a finite-dimensional vector space over a field of characteristic zero,and letgbe a Lie subalgebra ofgl(V). (1)All maximal fully reducible Lie subalgebras ofgare conjugate to each other underIg(Rad([g,g])). (2)Let R be a fully reducible subgroup ofGL(V).If R normalizesg,then R normalizes a maximal fully reducible Lie subalgebra ofg. Now letGbe an almost linear Nash group as before.In the rest of this section,denote by g and u the Lie algebras ofGand UG,respectively. Lemma 14.3One hasRad([g,g])⊂u. ProofBy Lemma 11.3,the Lie algebra g/u is reductive.Therefore, is semisimple.Note that is a solvable ideal of the semisimple Lie algebra(14.1).Therefore,(14.2)is the zero ideal,and this lemma follows. Fix a Nash homomorphismφ:G→GL(V)with a finite kernel,whereVis a finitedimensional real vector space.Then g is identified with a Lie subalgebra of gl(V). Lemma 14.4All maximal fully reducible Lie subalgebras ofgare conjugate to each other underUG. ProofThis is a direct consequence of Lemma 14.3 and the first assertion of Lemma 14.2. Fix a pair(l,K),where l is a maximal fully reducible Lie subalgebra of g,andKis a maximal compact subgroup of the normalizerof l inG.Lemma 14.4 and Theorem 4.2 imply that all such pairs are conjugate to each other underG.Denote byL0the analytic subgroup ofGwith Lie algebra l. Lemma 14.5The subgroup L0of G is a reductive Nash subgroup of G. ProofDenote bythe smallest Nash subgroup ofGcontainingL0.It is connected,sinceL0is so.Note that the set ofL0-stable subspaces ofVis the same as the set of-stable subspaces.Therefore,Vis completely reducible as a representation ofThis implies thatis reductive and its Lie algebra is fully reducible.The maximality of l then implies that=,and this lemma follows. PutL:=KL0,which is a Nash subgroup ofG.We want to show that Lemma 14.6One has=L0. ProofSinceL0is reductive,the unipotent radicalofLhas trivial intersection withL0.Then the quotient homomorphism is restricted to an injective Nash homomorphism from ULto an elliptic Nash group.Therefore,ULis trivial andLis reductive.Then the Lie algebra ofLis fully reducible and contains l,and hence equals l by the maximality of l.This proves this lemma. Since we have proved thatLis reductive,we know Lemma 14.7One hasl+u=g. ProofLetsbe a semisimple element of g.By Lemma 13.1,the replicais a Nash torus.Therefore,its Lie algebra Lieis fully reducible.By Lemma 14.4,there is an elementu∈UGsuch that This proves that l+u⊃gss.Then Lemma 13.2 implies that(l+u)/u⊃is dense in g/u by Theorem 13.1,one knows that(l+u)/u⊃g/u.Therefore,l+u=g. Combining(14.4)and Lemma 14.7,we get Recall thatdenotes the normalizer of l inG.Writefor its Lie algebra,and put u0:=∩u.Then is a direct product of Lie algebras.Consequently,we have Lemma 14.8Every connected reductive Nash subgroup ofis contained in L0. ProofIn view of(14.6),this lemma holds because every Nash homomorphism from a reductive Nash group to a unipotent Nash group is trivial. Lemma 14.9One has G=LUG. ProofBy(14.4)–(14.5),it suffices to show that every connected component ofGmeetsK.SinceKmeets every connected component ofit suffices to show that every connected component ofGmeetsLetg∈G.Then by Lemma 14.4,Adg(l)=Adu(l)for someu∈UG.Therefore,∈and this lemma follows. Lemma 14.9 implies thatLis a maximal reductive Nash subgroup ofG. Lemma 14.10Every reductive Nash subgroup R of G is contained in a conjugation of L. ProofBy Lemma 14.2,we assume without loss of generality thatR⊂.Then Lemma 14.8 implies that⊂L0.LetK′be a maximal compact subgroup ofR.Then Theorem 4.2 implies thatfor someg∈Therefore, Lemma 14.10 implies that all maximal reductive Nash subgroups ofGare conjugate toL(sinceG=LUG,they are actually conjugate toLunder UG).This finishes the proof of Theorem 14.1. We first recall some basic results concerning Cartan decompositions in the setting of connected semisimple Lie groups with finite centers. Proposition 15.1(see[12,Theorems 6.31,6.51 and Proposition 6.40])Let G be a connected semisimple Lie group with a finite center.Denote bygits Lie algebra.Let K be a maximal compact subgroup of G.Then the followings hold: (1)There exists a unique continuous involutionof G such that=K. (2)Denote bypthe(−1)-eigenspace ingof the differential of ,and then the map is a diffeomorphism. (3)All maximal abelian subspaces ofpare conjugate to each other under the adjoint action of K. (4)For every x∈p,the linear operator is semisimple and all its eigenvalues are real. Here “involution” means an automorphism of order 1 or 2;anddenotes the fixed-point set ofθKinG(the similar notation will be used without further explanation). In this section,we investigate Cartan involutions for all reductive Nash groups.LetGbe a reductive Nash group in the rest of this section. Definition 15.1A Cartan involution of G is a Nash involution of G whose fixed-point set is a maximal compact subgroup of G. Here“Nash involution” means an involution which is simultaneously a Nash map.The first result of this section we intend to prove is the following theorem. Theorem 15.1The map is bijective. We begin with the following lemma. Lemma 15.1Theorem15.1holds if G is a connected semisimple Nash group or a Nash torus. ProofIfGis a connected semisimple Nash group,then all Lie group automorphisms ofGare Nash automorphisms.Therefore,this lemma is implied by the first assertion of Proposition 15.1.IfGis a Nash torus,thenG=is the unique maximal compact subgroup ofG.Moreover, is the unique Cartan involution ofG.Therefore,this lemma also holds. Denote by g the Lie algebra ofG,and write where z denotes the center of g,and s:=[g,g].As before,denote byZandSthe analytic subgroups ofGwith Lie algebras z and s,respectively.ThenZis a Nash torus,andSis a connected semisimple Nash group.LetKbe a maximal compact subgroup ofG,and put Lemma 15.2One has K∩Z=,which is the unique maximal compact subgroup of Z;K0is a maximal compact subgroup of S;and ProofThe equalityK∩Z=is obvious.Denote byφ:S×Z→the multiplication map.It is a finite-fold covering homomorphism.Note thatis a maximal compact subgroup ofTherefore,is a maximal compact subgroup ofS×Z,which has the formwhereis a maximal compact subgroup ofS.We have which implies thatSinceis already a maximal compact subgroup ofS,we have thatK0=This proves this lemma. Lemma 15.3The map(15.1)is injective. ProofLetθandθ′be two Cartan involutions ofGsuch thatThenand=Therefore,Lemmas 15.1–15.2 imply that The lemma then follows asG=SZ. Using Lemmas 15.1–15.2,writefor the unique Cartan involution ofSwith a fix-point setK0.WriteθZfor the unique Cartan involution ofZ. Lemma 15.4There exists a unique Cartan involution of G◦extending both θSand θZ. ProofUniqueness holds asG◦=SZ.Note thatS∩Zis contained in bothK0andZe.HenceθSandθZhave a common extension to an involution ofG◦.One checks that this involution hasK◦as its fixed-point set,and hence it is a Cartan involution. Denote byθ◦the Cartan involution ofG◦of Lemma 15.4.Define a map It is routine to check that(15.2)is a well-defined Nash involution ofGwhose fixed-point set equalsK.This finishes the proof of Theorem 15.1. Now letθbe the Cartan involution ofGso thatGθ=K.Still denote byθ:g→g its differential.Denote by p the(−1)-eigenspace ofθin g. Proposition 15.2The map is a diffeomorphism. ProofWithout loss of generality,assume thatGis connected.The second assertion of Proposition 15.1 as well as its analog for Nash tori implies that the map is a diffeomorphism.This descends to a deffeomorphism where The lemma then follows since the smooth map(15.3)is obviously identified with(15.5). Lemma 15.5One hasp⊂gh. ProofWithout loss of generality,assume thatGis connected and semisimple.Letx∈p.By uniqueness of Jordan decompositions,the quality implies that=−xe,that is,xe∈p.Likewise,xh∈p andxu∈p.Therefore,it suffices to show that p∩ge={0}and p∩gu={0}.Note that for everyy∈the linear operator ady:g→g is semisimple and all its eigenvalues are purely imaginary.Together with the last assertion of Proposition 15.1,this implies that={0}.The equality p∩gu={0}is proved similarly. Proposition 15.3Each θ-stable Nash subgroup G1of G is reductive and equals K1exp(p1),where ProofLetg=kexp(x)∈G1,wherek∈Kandx∈p.Then Then Lemma 15.5 and Proposition 9.2 imply that exp(Rx)⊂G1.Consequently, Therefore, Denote byU1the unipotent radical ofG1.Then it is also aθ-stable Nash subgroup ofG.Therefore, It is clear that={0}.Therefore,U1is trivial andG1is reductive. The following result is an obvious consequence of the third assertion of Proposition 15.1. Proposition 15.4All maximal abelian subspaces ofpare conjugate to each other under K. Let a be a maximal abelian subspace of p.Denote byAthe analytic subgroup ofGwith Lie algebra a. Proposition 15.5The analytic subgroup A is a hyperbolic Nash subgroup of G. ProofDenote bythe centralizer of a inG,which is aθ-stable Nash subgroup ofG.Note that(Lie)∩p=a,since a is maximal abelian in p.Therefore,by Proposition 15.3, Denote byZ1the center of,and thenAequals the identity connected component of the Nash subgroup Therefore,Ais a Nash subgroup. Note thatAis abelian and all elements ofAare hyperbolic.Therefore,Ais hyperbolic by Proposition 8.3. Lemma 15.6The setexp(p)is a close Nash submanifold of G. ProofThe set exp(p)is a closed submanifold ofGby Proposition 15.2.It is semialgebraic,since it is equal to the image of the Nash map Combining Propositions 15.2,15.4 and Lemma 15.6,we obtain the following proposition. Proposition 15.6One has G=KAK,and the multiplication map is a Nash diffeomorphism. Write where a∗denotes the space of all real valued linear functionals on a,and Then the set is a root system in.Fix a positive system ∆(g,a)+⊂∆(g,a),and put Then n is a Lie subalgebra of g.Denote byNthe analytic subgroup ofGwith Lie algebra n. Proposition 15.7The analytic subgroup N is a unipotent Nash subgroup of G. ProofWithout loss of generality,assume thatGis semisimple and connected.Denote bya0the element of a such thatα(a0)=1 for all simple rootsαin ∆(g,a)+.For every integeri,denote Put Thenis a unipotent Nash subgroup of GL(g)with Lie algebra Consider the adjoint representation and its differential Note that=n.Therefore,the Nash subgroupofGhas the Lie algebra n.HenceNequals the identity connected component ofwhich is a Nash subgroup ofG.SinceGis assumed to be semisimple,the adjoint representation ofNon g has a finite kernel.Then Lemma 5.6 implies thatNis unipotent. Theorem 15.2The multiplication map is a Nash diffeomorphism. ProofWithout loss of generality,assume thatGis connected.The map(15.6)is clearly a Nash map.We only need to show that it is a diffeomorphism.This is known whenGis semisimple(see[12,Theorem 6.46]).The same argument as in Proposition 15.2 reduces the general case to the case whenGis semisimple. As a corollary of Theorem 15.2,we have the following proposition. Proposition 15.8An almost linear Nash group is elliptic if it consists elliptic elements only. ProofIf an almost linear Nash group consists only elliptic elements,then its unipotent radical is trivial,and is thus reductive.Then Theorem 15.2 implies that it is compact. The same proof as Proposition 15.8 shows the following proposition. Proposition 15.9An almost linear Nash group is hyperbolic if it consists hyperbolic elements only. Recall from Section 1 that an almost linear Nash groupGis said to be exponential ifGe={1}.The following lemma is obvious. Lemma 16.1An almost linear Nash group is exponential if and only if all its elements are exponential. Proposition 8.1 implies the following lemma. Lemma 16.2All Nash quotient groups of exponential Nash groups are exponential Nash groups. LetGbe an almost linear Nash group,and letKbe a maximal compact subgroup ofG. Lemma 16.3The almost linear Nash group G is exponential if and only if K is trivial. ProofThe lemma is clear,since Lemma 16.4If G is reductive and exponential,then G is hyperbolic. ProofThe lemma follows by Lemma 16.3 and Proposition 15.6. Lemma 16.5The almost linear Nash group G is exponential if and only if G/UGis a hyperbolic Nash group. ProofIn view of Lemma 16.2,the “only if” part is implied by Lemma 16.4.To prove the“if” part,assume thatG/UGis a hyperbolic Nash group.Then under the quotient map the image ofGeis contained in Therefore,which implies that={1}. Using Levi decompositions,Lemma 16.5 implies that every exponential Nash group is connected,simply connected and solvable. Lemma 16.6If G is unipotent or hyperbolic,then there is no proper co-compact Nash subgroup of G. ProofThe hyperbolic case is obvious.Assume thatGis unipotent.We prove this lemma by induction on dimG.It is trivial when dimG=0.Assume that dimG>0 and this lemma holds for unipotent Nash groups of smaller dimensions. LetHbe a co-compact Nash subgroup ofG.Denote byZthe center ofG.It is a Nash subgroup ofGof positive dimension.Note thatZHis a Nash subgroup ofG,andZH/His a closed subset ofG/H.Therefore, is compact.Since the lemma obviously holds for abelian unipotent Nash groups,we have thatZ∩H=Z,or equivalently,H⊃Z.ThenH/Zis a co-compact Nash subgroup of the unipotent Nash groupG/Z.Since dimG/Z Lemma 16.7If G is exponential,then there is no proper co-compact Nash subgroup of G. ProofLetHbe a co-compact Nash subgroup ofG.Using Proposition 3.5,we get a closed orbitO⊂G/Hunder left translations by UG.SinceOis compact,Lemma 16.6 implies thatOhas only one point,sayH.Thenwhich implies thatis a normal subgroup ofG.NowH/UGis a co-compact Nash subgroup of the hyperbolic Nash groupG/.Lemma 16.6 implies thatin other words,H=G. The following is the Borel fixed-point theorem in the setting of Nash groups. Theorem 16.1Let G×M→M be a Nash action of G on a non-empty Nash manifold M.If G is exponential and M is compact,then the action has a fixed-point. ProofUsing Proposition 3.5,we get a closedG-orbitO⊂M.ThenOis compact and Lemma 16.7 implies thatOhas only one point. Lemma 16.8There exists an exponential Nash subgroup B of G such that the multiplication map K×B→G is a Nash diffeomorphism. ProofWithout loss of generality,assume thatGis reductive(otherwise,take a Levi component ofGcontainingK).Then the groupANof Theorem 15.2 fulfills the requirement of this lemma. Lemma 16.9If G is not exponential,then G has a proper co-compact Nash subgroup. ProofThe groupBof Lemma 16.8 is a proper co-compact Nash subgroup ofG. Recall the following lemma. Lemma 16.10(see[13,Section I.1,Theorem 1])Let H be a connected,simply connected,solvable Lie group with Lie algebrah.If the exponential mapexp:h→H is either injective or surjective,then it is a diffeomorphism. Denote by g the Lie algebra ofG. Proposition 16.1The almost linear Nash group G is exponential if and only if the exponential map is a diffeomorphism. ProofThe “only if” part is implied by Proposition 9.1 and Lemma 16.10.To prove the“if” part of the proposition,assume that(16.1)is a diffeomorphism.ThenGis connected.Therefore,Kis connected and the exponential map is injective,where k denotes the Lie algebra ofK.This forcesKto be trivial.Therefore,Gis exponential by Lemma 16.3. Lemma 16.11For each co-compact Nash subgroup H of G,one has thatdimH≥dimG/K. ProofLetBbe as in Lemma 16.8.By Theorem 16.1,the left translation action ofBonG/Hhas a fixed point,sayH.ThenBH⊂H,which implies that Denote by(R)the Nash subgroup of(R)consisting all upper-triangular matrices with positive diagonal entries(n≥0).Its Lie algebra(R)consists all upper-triangular matrices in g(R).It is obvious that(R)and all its Nash subgroups are exponential Nash groups.Conversely,we have the following lemma. Lemma 16.12Every exponential Nash group H is Nash isomorphic to a Nash subgroup ofBn(R)for some n≥0. ProofFix a Nash representationVofHwith a finite kernel.By Lemma 16.3,the representation is actually faithful.Consider the induced action ofHon the compact Nash manifold of all full flags inV.Then Theorem 16.1 implies that the action has a fixed-point,that is,Hstabilizes a full flag inV.Therefore,there exists an injective Nash homomorphismφ:wheren:=dimV,anddenotes the Nash subgroup ofof upper-triangular matrices.SinceHis connected,φ(H)is contained inand this lemma follows. Theorem 16.2Every exponential Nash subgroup of G is contained in a maximal one,and all maximal exponential Nash subgroups of G are conjugate to each other in G. ProofLetBbe as in Lemma 16.8.LetHbe an exponential Nash subgroup ofG.By Theorem 16.1,the left translation action ofHonG/Bhas a fixed-point,say,g0B.ThenHg0B⊂g0B,and consequently,His contained in a conjugation ofB.Therefore,Bhas the largest dimension among all exponential Nash subgroups ofG.In particular,Bis a maximal exponential Nash subgroup ofG(since all exponential Nash groups are connected).This proves this theorem. Theorem 16.3A Nash subgroup B of G is a maximal exponential Nash subgroup if and only if the multiplication map K×B→G is a Nash diffeomorphism. ProofLetBbe a Nash subgroup ofG.We first prove the “if” part of the theorem.So assume that the multiplication mapK×B→Gis a Nash diffeomorphism.ThenBis connected.LetK′be a maximal compact subgroup ofB.Applying Lemma 16.8 toB,we get an exponential Nash subgroupB′ofBso that the multiplication mapK′×B′→Bis a Nash diffeomorphism.ThenB′is co-compact inG.Hence,by Lemma 16.11, Therefore,B′=B,andBis an exponential Nash subgroup ofG.Then the proof of Theorem 16.2 shows thatBis a maximal exponential Nash subgroup ofG. To prove the “only if” part of the theorem,assume thatBis a maximal exponential Nash subgroup ofG.Using Lemma 16.9,we take an exponential Nash subgroupB0ofGso that the multiplication map The proof of Theorem 16.2 shows thatB0is a maximal exponential Nash subgroup ofG.By Theorem 16.2, Writeg0=whereandNote that(16.3)implies that the multiplication map is a Nash diffeomorphism.The “only if” part of the theorem then follows as=B. Theorem 16.4Every hyperbolic Nash subgroup of G is contained in a maximal one,and all maximal hyperbolic Nash subgroups of G are conjugate to each other in G. ProofFix a maximal exponential Nash subgroupBofG,and fix a Levi componentAofB.LetHbe a hyperbolic Nash subgroup ofG.Then by Theorem 16.2,a conjugation ofHis contained inB.Theorem 14.1 further implies that a conjugation ofHis contained inA.As in the proof of Theorem 16.2,we know thatAis a maximal hyperbolic Nash subgroup by reason of dimension.This proves the theorem. Lemma 16.13If G is exponential,then every unipotent Nash subgroup of G is contained inUG. ProofLetUbe a unipotent Nash subgroup ofG.Then the quotient homomorphism has trivial restriction toU.Therefore,U⊂UG. In view of Lemma 16.13,a similar argument as Theorem 16.4 implies the following theorem. Theorem 16.5Every unipotent Nash subgroup of G is contained in a maximal one,and all maximal unipotent Nash subgroups of G are conjugate to each other in G. By the preceding arguments,we know that for each maximal exponential Nash subgroupBofG,its unipotent radical UBis a maximal unipotent Nash subgroup ofG,and each Levi component ofBis a maximal hyperbolic Nash subgroup ofG. In this last section,we collect some results of the previous sections to explain the proofs of those propositions and theorems which occur in Section 1. Proposition 1.1 is a restatement of Proposition 3.8. Recall that Proposition 1.2 asserts the following:An almost linear Nash group is elliptic,hyperbolic or unipotent if and only if all of its elements are elliptic,hyperbolic or unipotent,respectively.The“only if” part of Proposition 1.2 is trivial.The elliptic case and the hyperbolic case of the “if” part are proved in Propositions 15.8–15.9,respectively.To prove the “if” part in the unipotent case,letGbe an almost linear Nash group consisting unipotent elements only.ThenGis exponential.Hence,a Levi component ofGis a hyperbolic Nash group,which has to be trivial.Therefore,Gis unipotent.This finishes the proof of Proposition 1.2. Proposition 1.3 consists two assertions.The first one is the following proposition. Proposition 17.1Let G be an almost linear Nash group which is elliptic,hyperbolic or unipotent.Then all of its Nash subgroups and Nash quotient groups are elliptic,hyperbolic or unipotent,respectively. ProofThe assertion for Nash subgroups is obvious.The assertion for Nash quotient groups appears in Propositions 4.1,6.2 and 7.6. The second assertion of Proposition 1.3 is the following proposition. Proposition 17.2Let G be an almost linear Nash group.If G has a normal Nash subgroup H so that H and G/H are both elliptic,both hyperbolic or both unipotent,then G is elliptic,hyperbolic or unipotent,respectively. Assume that bothHandG/Hare elliptic.The image ofGhunder the quotient map is contained in(G/H={1}.Therefore,⊂H,which implies thatGh={1}.Similarly,={1}.Therefore,G=,and Proposition 1.2 implies thatGis elliptic. The same argument proves this proposition in the hyperbolic and unipotent cases. As already mentioned,Theorem 1.1 is a combination of Lemmas 4.1–4.3,and Theorem 1.2 is a combination of Propositions 5.1,5.3–5.5.Theorem 1.3 is a restatement of Theorem 1.3.Theorem 1.4 is the same as Theorem 8.1. Theorem 1.5 consists of five assertions.The second one is obvious.The others are respectively proved in Lemma 10.1,Propositions 10.3,10.2 and 10.1. For Theorem 1.6,it is obvious that(b)⇒(a),and Theorem 11.2 asserts that(a)⇒(b).Lemma 14.1 asserts that(a)⇔(c).Theorem 12.1 implies that The equivalence(a)⇔(f)is proved in Lemma 11.1,and(a)⇔(g)is proved in Theorem 11.1.Therefore,Theorem 1.6 holds. For Theorem 1.7,(a)⇔(b)is implied by Lemma 16.3,and(a)⇔(c)is implied by Lemmas 16.7 and 16.9.The equivalence(a)⇔(d)is proved in Lemma 16.5,(a)⇔(e)is implied by Lemma 16.12,and(a)⇔(f)is proved in Proposition 16.1.By Theorem 16.1,(a)⇒(g),and by Lemma 16.9,(g)⇒(a).In conclusion,Theorem 1.7 holds. Theorem 1.8 is contained in Theorems 4.2,14.1,16.2,16.4–16.5. Finally,Theorem 1.9 is contained in Theorem 14.1,and Theorem 1.10 is contained in Theorem 16.3. [1] Basu,S.,Ollack,R.and Roy,M.F.,Algorithms in Real Algebraic Geometry,Algorithms and Computation in Mathematics,Springer-Verlag,Berlin,2003. [2] Bochnak,J.,Coste,M.and Roy,M.F.,Real Algebraic Geometry,Ergebnisse der Math.,Vol.36,Springer-Verlag,Berlin,1998. [3] Borel,A.,Linear Algebraic Groups,2nd ed.,Graduate Texts in Mathematics,Vol.126,Springer-Verlag,New York,1991. [4] Borel,A.,Semisimple Groups and Riemannian Symmetric Spaces,Texts and Readings in Mathematics 16,Hindustan Book Agency,1998. [5] Borel,A.and Mostow,G.D.,On semi-simple automorphisms of Lie algebras,Ann.Math.,61,1955,389–504. [6] Cartier,P.,A primer of Hopf algebras,Frontiers in Number Theory,Physics,and Geometry II,On Conformal Field Theories,Discrete Groups and Renormalization(Papers from the meeting,Les Houches,France,March 9–21,2003,537–615),Springer-Verlag,Berlin,2007. [7] Coste,M.,An Introduction to Semialgebraic Geometry,RAAG Notes,Institut de Recherche Mathmatiques de Rennes,2002. [8] Dixmier,J.,L’application exponentielle dans les groupes de Lie resolubles,Bull.Soc.Math.France,85,1957,113–121. [9] Goodman,R.and Wallach,N.R.,Symmetry,Representations and Invariants,Graduate Texts in Mathematics,255,Springer-Verlag,New York,2009. [10]Helgason,S.,Differential Geometry,Lie Groups,and Symmetric Spaces,Graduate Studies in Mathematics,34,A.M.S.,Providence,RI,2001. [11]Jacobson,N.,Completely reducible Lie algebras of linear transformations,Proc.Amer.Math.Soc.,2,1951,105–113. [12]Knapp,A.W.,Lie Groups Beyond an Introduction,2nd ed.,Birkhäuser,Boston,1996. [13]Leptin,H.and Ludwig,J.,Unitary Representation Theory of Exponential Lie Groups,W.de Gruyter,Berlin,1994. [14]Milne,J.S.,Lie Algebras,Algebraic Groups,and Lie Groups,2012.http://www.jmilne.org/math/CourseNotes/LAG.pdf [15]Mostow,G.D.,Fully reducible subgroups of algebraic groups,Amer.J.Math.,78,1956,200–221. [16]Shiota,M.,Nash Manifolds,Lect.Notes Math.,1269,Springer-Verlag,Berlin,Heidelberg,New York,London,Paris,Tokyo,1987. [17]Shiota,M.,Nash Functions and Manifolds in Lectures in Real Geometry,F.Broglia(ed.),W.de Gruyter,Berlin,New York,1996. [18]Warner,F.W.,Foundations of Differentiable Manifolds and Lie Groups,Graduate Texts in Mathematics,94,Springer-Verlag,New York,1983.3 Nash Groups and Almost Linear Nash Groups








4 Elliptic Nash Groups
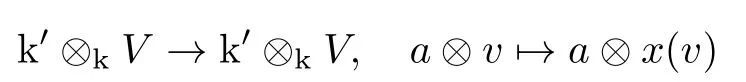

5 Unipotent Nash Groups





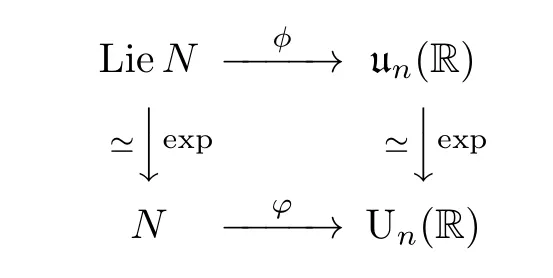
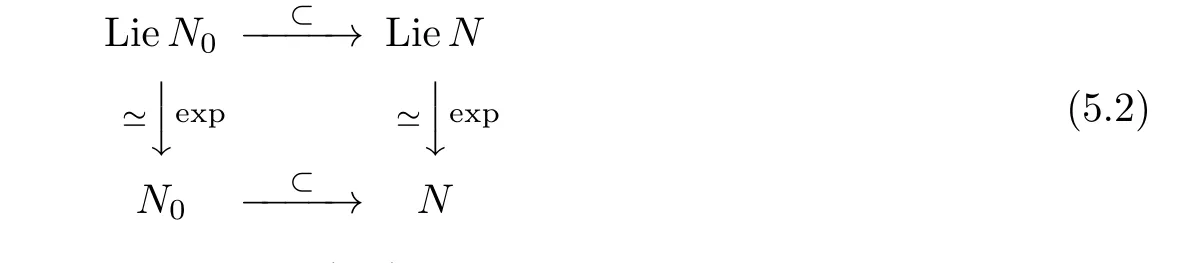
6 Hyperbolic Nash Groups
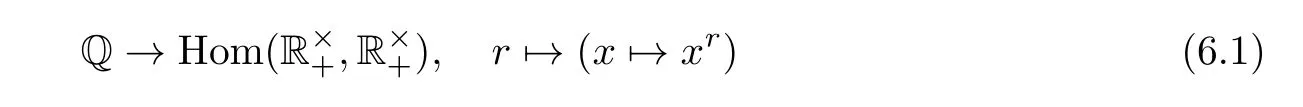
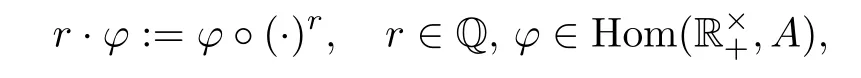



7 Disjointness of Elliptic,Hyperbolic and Unipotent Nash Groups
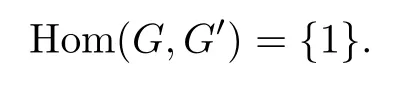










8 Jordan Decompositions



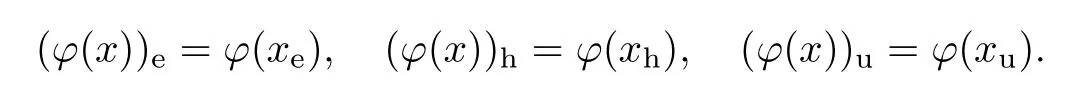




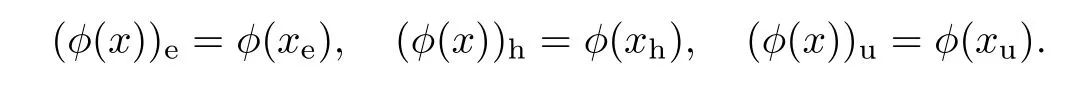
9 Exponential Elements
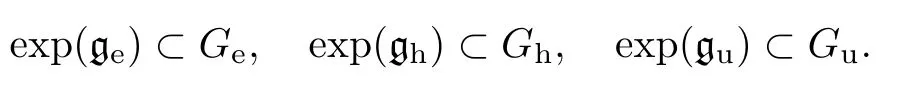


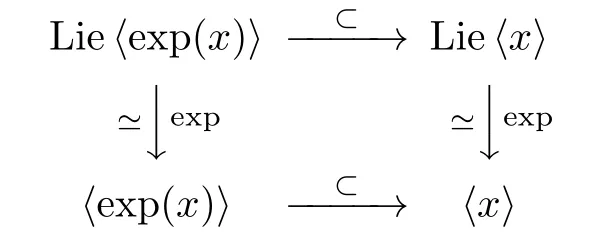



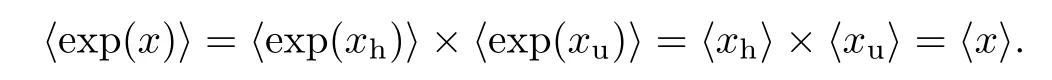
10 Semisimple Nash Groups
11 Reductive Nash Groups

12 Trace Forms and Reductivity


13 Semisimple Elements

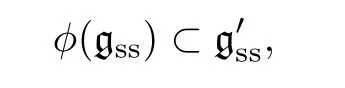

14 Levi Decompositions






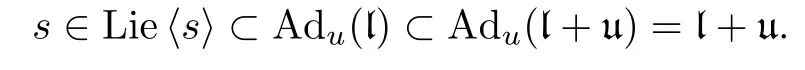

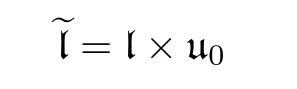
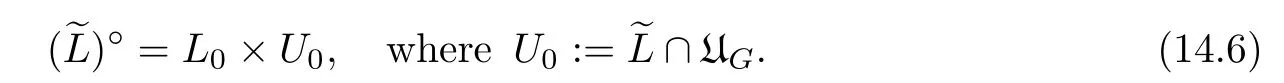
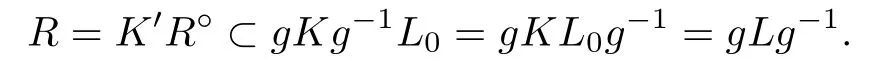
15 Cartan Decompositions and Iwasawa Decompositions

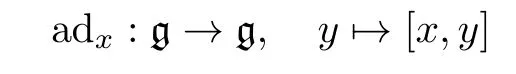


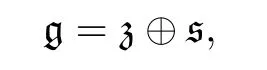










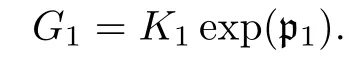
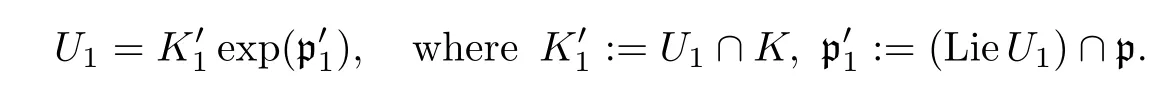
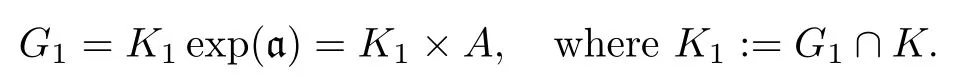

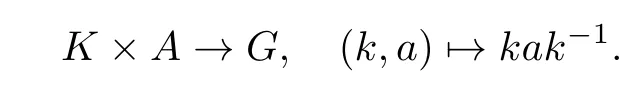

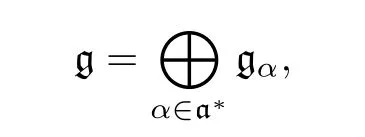








16 Exponential Nash Groups










17 About Proofs of the Results in Section 1


 Chinese Annals of Mathematics,Series B2015年3期
Chinese Annals of Mathematics,Series B2015年3期
