Lie Bialgebras of Generalized Loop Virasoro Algebras∗

Henan WUSong WANGXiaoqing YUE

1 Introduction

As the universal central extension of the infinite-dimensional Lie algebra(namely,the Witt algebraW1)of the linear differential operatorsof the Laurent polynomial algebrathe well-known Virasoro algebra plays a very fundamental role in conformal field theory,string theory,the theory of vertex operator algebras and the representation theory of Kac-Moody algebras as well as extended affine Lie algebras(see,e.g.,[1,2,6]).Various generalizations of the Virasoro algebra and other closely related algebras were objects of intensive studies in literature(see,e.g.,[7,9,12–17,21]).Among them,the one that naturally occurs in extended affine Lie algebras is the(generalized)loop Virasoro algebra(and more generally,the map Virasoro algebras),whose structure and representation theories are studied in[7,9,17,21].

In this paper,we are interested in considering Lie bialgebra structures on generalized loop Virasoro Lie algebras and generalized map Virasoro Lie algebras.Lie bialgebras as well as their quantizations provide important tools in searching for solutions of quantum Yang-Baxter equations and in producing new quantum groups(see,e.g.,[3–4]).Thus,there are a number of papers on Lie bialgebra structures in literature.For instance,Lie bialgebra structures on the Witt,one-sided Witt and Virasoro algebras were shown in[8,20]to be coboundary triangular,which can be obtained from their nonabelian two dimensional Lie subalgebras.Moreover,Liebialgebra structures on the one-sided Witt algebra were completely classified in[8].Furthermore,Lie bialgebra structures on Lie algebras of generalized Witt type and Weyl type were considered in[10,22].

We remark that the objects studied in this paper are Γ-graded Lie algebras(see(3.1)),however,they are not finitely Γ-graded,and not finitely generated as Lie algebras in general,in sharp contrast to the Witt,one-sided Witt and Virasoro algebras.Thus when we tackle problems associated with such objects,as stated in[17,21],the classical techniques such as that in[5]may not be directly applied to the situation here.Instead,some new techniques or strategies must be employed as can be seen in the proof of Lemma 3.3.This is one of our motivations.The main results presented in this paper are summarized in Theorems 3.1 and 4.1,which state that all Lie bialgebra structures under consideration are coboundary triangular.As predicted,the results are not surprising.However,a Lie bialgebra having a coboundary triangular structure does not mean that it is not interesting,as one can see from[11]that dualizing a coboundary triangular Lie bialgebra may produce new Lie algebras.This will be persuaded in a sequel.

This paper proceeds as follows.In Section 2,the preliminaries of Lie bialgebras are recalled.In Section 3,Lie bialgebra structures on generalized loop Virasoro algebras are proven to be coboundary triangular.Then we generalize the results in Section 3 to the case of map Virasoro algebras in Section 4.

2 Preliminaries

Let us recall some concepts related to Lie bialgebras now.Throughout this paper,F denotes a field of characteristic zero and all the tensor products are taken over F.LetLbe a vector space over F.Denote byτthe twist map ofL⊗L,namely,

Denote byεthe map which cyclically permutes the coordinates ofL⊗L⊗L,i.e.,

Then the definition of a Lie algebra can be stated as follows.

Definition 2.1Let L be a vector space overF,and ϕ:L⊗L→L be a linear map.The pair(L,ϕ)is called a Lie algebra,if the following conditions hold:

where1denotes the identity map on L.

The operatorϕis usually called the bracket ofL.Dually,we get the definition of Lie coalgebras.

Definition 2.2Let L be a vector space overFand∆:L→L⊗L be a linear map.The pair(L,∆)is called a Lie coalgebra,if

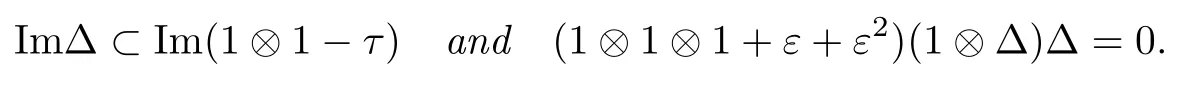
The map∆is called the cobracket ofL.Combining the algebra and coalgebra structures under some compatibility condition,we obtain the definition of a Lie bialgebra as follows.

Definition 2.3A Lie bialgebra is a triple(L,ϕ,∆),where(L,ϕ)is a Lie algebra,(L,∆)is a Lie coalgebra and

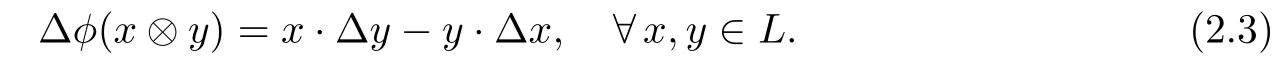
Note that the compatibility condition(2.3)is equivalent to that∆is a derivation.

Definition 2.4A coboundary Lie bialgebra is an(L,ϕ,∆,r),where(L,ϕ,∆)is a Lie bialgebra and γ∈Im(1⊗1−τ),such that∆is a coboundary of r,i.e.,for arbitrary x∈L,

Denote byU(L)the universal enveloping algebra ofLand 1 the identity element ofU(L).For anyr=∈L⊗L,defineandc(r)to be the elements ofU(L)⊗U(L)⊗U(L)by

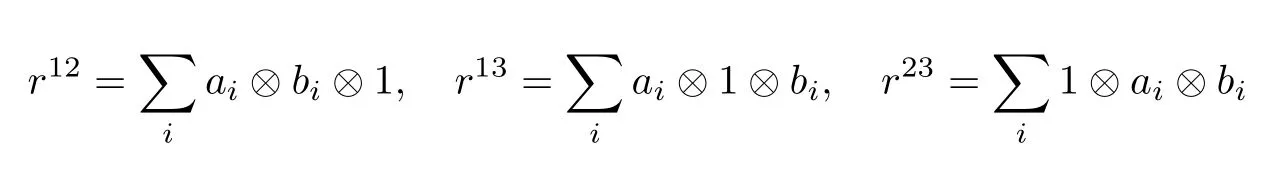
and

The following result is due to Drinfeld[4].

Theorem 2.1Let(L,ϕ)be a Lie algebra.Then for some r∈Im(1−τ),∆ = ∆rendows(L,ϕ,∆)with a Lie bialgebra structure if and only if r satisfies the following modified Yang-Baxter equation(MYBE):

Furthermore,one has the following definition.

Definition 2.5A coboundary Lie bialgebra(L,ϕ,∆,r)is called triangular,if r satisfies the following classical Yang-Baxter equation(CY BE):

3 Lie Bialgebras of Generalized Loop Virasoro Algebras

Let Γ be an additive subgroup of F,and F[Γ]be the group algebra of Γ with basisα∈Γ}.DenoteW(Γ)=F[Γ]∂(where∂()=α),which is usually referred to as the(generalized)Witt algebra or(the generalized centerless)Virasoro algebra(see[19]).SinceW(Γ) ≅W(if ΓΓ′by[18],and for any 0α∈Γ,we have ΓReplacing Γ byif necessary,we always assume that 1∈Γ.We denote(Γ)=W(Γ)which is referred to as a(generalized)loop Witt algebra or a(generalized)loop(centerless)Virasoro algebra.We can write(Γ)as

with brackets

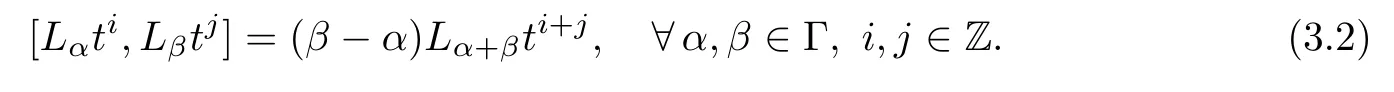
We use the notationin the remainder of this section.

Denote byVthe tensor productWL(Γ)⊗WL(Γ).SinceWL(Γ)is a Γ-graded Lie algebra,Vadmits a natural Γ-gradedWL(Γ)-module structure under the adjoint diagonal action ofWL(Γ).Precisely,V=whereVαis spanned byβ+γ=α,i,j∈Z}.Denote by Der(WL(Γ),V)and Inn(WL(Γ),V)the vector spaces of all derivations and inner derivations fromWL(Γ)toV,respectively.It is well-known that the first cohomology group ofWL(Γ)with coefficients in the moduleVis isomorphic to Der(WL(Γ),V)/Inn(WL(Γ),V).Denote by(Der(WL(Γ),V))αthe space of derivations of degreeα.Then we have the following result through some arguments analogous to that in[10].

Lemma 3.1The spaceDer(WL(Γ),V)can be decomposed into

where(Der(WL(Γ),V))α⊂Inn(WL(Γ),V)for any α0.

We can also obtain the following result easily,which is useful in our paper.

Lemma 3.2Let D∈Der(WL(Γ),V)be a derivation,such that D()=0.Then D∈(Der(WL(Γ),V))0.

ProofLetDact on the equation=αWe have=αD().SoD()∈Vαand the assertion follows.

Fixiandj,and let=span{⊗|α,β∈Γ}=spanα,β∈Γ}.ThenV=⊕which is a Z2-graded space.Consider the subalgebraW=span{|α∈Γ}ofWL(Γ).ThenWis actually isomorphic to the generalized centerless Virasoro algebra andis aW-module.It is easy to show thatW⊗WasW-modules.

For the sake of computation,we will adopt the following description ofVin the rest of this section.As a vector space,V(W⊗W)⊗(W⊗W)[x,,y,],which is actually the space of formal Laurant polynomials in two variables with coefficients inW⊗W.Explicitly,this isomorphism mapsNow the action ofWL(Γ)onVis given by

Then we have the following result.

Lemma 3.3For D∈Der((Γ),V),there is a vector v∈V,such that(D−Dv)(W)=0,where Dvis an inner derivation defined by·v for any α∈Γand i∈Z.

ProofConsider the restriction ofDtoW,we haveD|W∈Der(W,V).We also denoteD|WbyDfor convenience.As aW-module,V=(see[10]),where∈Der(W,).We should remark that this formula holds in the sense that whenDactson a given vector,there exist only finite nonzero terms on the right side.Referring to[8]or[10],one hasH1(W,W⊗W)=0.So there exists some∈such that=whereis an inner derivation with respect toWe will show that the formulaD=is just a finite sum in the rest of the proof.Then we can deduce thatDis an inner derivation.

If Γ is a finitely generated free abelian group(see,e.g.,Z,Z2),Wis finitely generated as a Lie algebra.Then we can deduce thatD(W)is contained in a finite direct sum ofThusD=∑is a finite sum andD=Dvwherev=

For an arbitrary group Γ,we have to use some completely different arguments.Consider the finite setX={(i,j)|(·,,·)(0,0,0)}.The complement ofXin Z×Z is={(i,j)|·=·=·=0}.Given a pair(i,j)∈assume=wherea(α,β)∈F.Since

we have(β+α)a(α,β)=0.Then it reduces to the case that=fora(γ)∈F.

Since

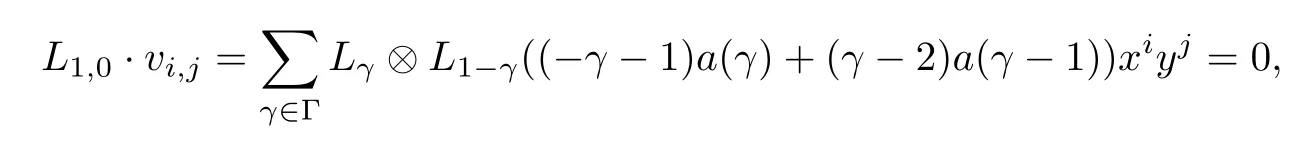
we have

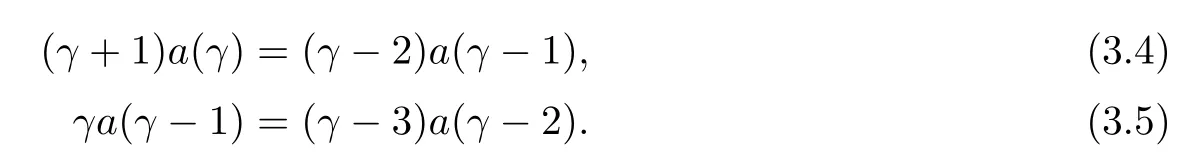
Similarly,

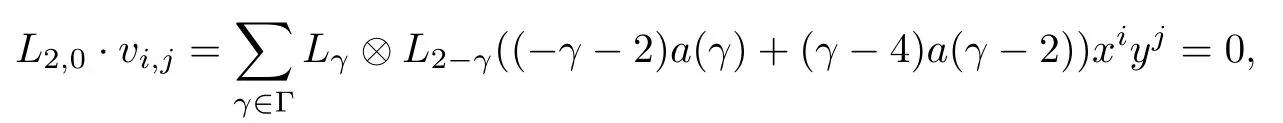
and we obtain

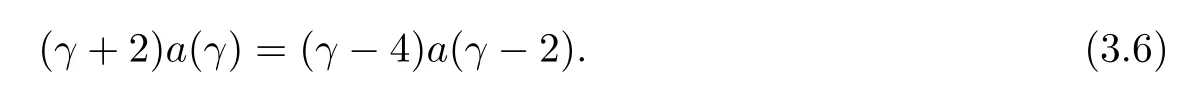
From the linear equations(3.4)–(3.6),we havea(γ)=0.Then=0 and{(i,j)|0}⊂X.ThusD=is a finite sum andD=Dv,wherev=So Der(W,V)==Inn(W,V).This completes the proof.

Lemma 3.4Every derivation from(Γ)to V is inner,i.e.,(WL(Γ),V)=0.

ProofTake a derivationDfrom(Γ)toV.From Lemma 3.3,replacingDbyD−for somev∈V,we can assumeD(W)=0.Then we haveD∈(Der(WL(Γ),V))0from Lemma 3.2.Assume thatD()=whereand=0.

LettingDact on(3.2),we have

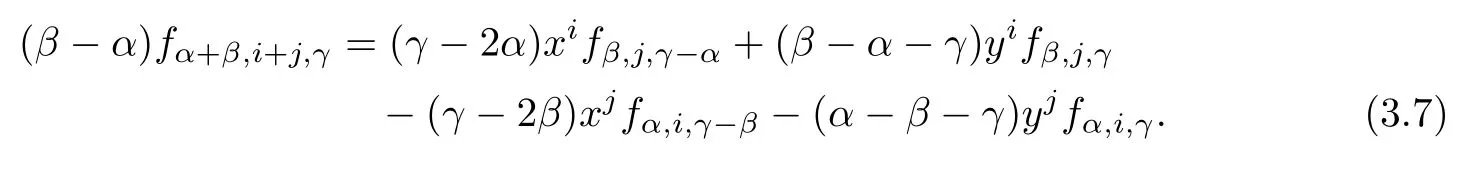
Settingβ=−αin(3.7),we have

Settingα=β=0 in(3.7),we have

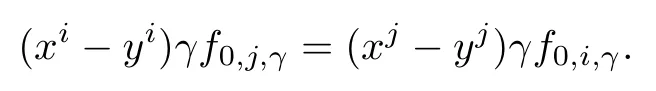
Ifγ0,we have

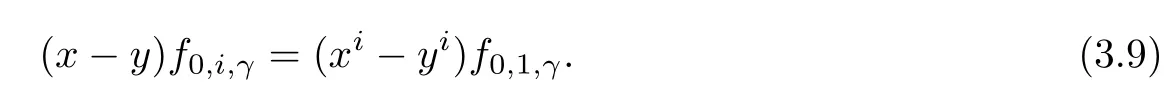
Settingβ=0 andi=0 in(3.7),we have

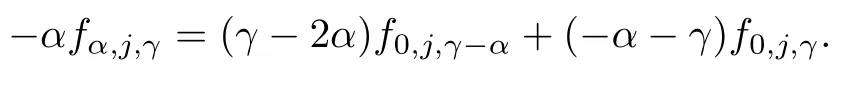
Substituting this formula into(3.8),we obtain that

Ifαγ,α−γandγ0,multiplyingx−yon both sides of the above equation,we have

SinceD()=there are only finite nonzero terms on the right-hand side.We can choose someα,such that−0,=0 and=0.Then we deduce that=0 ifγ0.Consequently,=0 for anyγ0 from(3.9).

Now it reduces to the case that[x,,y,].Assume thatD()=L0⊗Thenfor anyα0 from(3.10).Settingγ=αin(3.8),we get

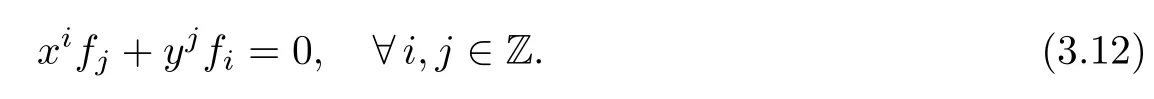
Hence we havefi=0 for anyi∈Z.ThusD=0.

Lemma 3.5Suppose r∈V,such that a·r∈Im(1⊗1− τ)for all a∈WL(Γ).Then r∈Im(1⊗1−τ).

ProofAssume thatr=Since 1⊗1−τis a homogenous operator of degree 0,a·r∈Im(1⊗1−τ)impliesa·rα∈Im(1⊗1−τ).Since=we can obtainrα∈Im(1⊗1− τ)for anyα0.Sor=r0=(x,y),where(x,y)∈F[x,x−1,y,y−1].And we have·r=∈Im(1⊗1−τ).Note that Im(1⊗1−τ)=Ker(1⊗1+τ)andThen=0.So(x,y)+(y,x)=0 for anyα0.Then∈Im(1⊗1−τ)ifα0.It reduces to the case thatr=∈Im(1⊗1−τ).We have=0 for anyα∈Γ.Then we obtainr∈Im(1⊗1−τ).This completes the proof.

Lemma 3.6Suppose that a vector c∈satisfies a·c=0for all a∈WL(Γ).Then c=0.

ProofAssumec=where

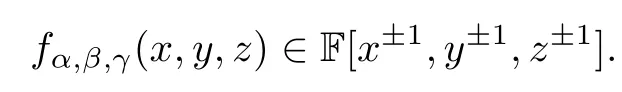
Choose an order on Γ compatible with the group structure on Γ.Then we have an induced lexicographic order on Γ×Γ×Γ.Let=max{(α,β,γ)|Take aδ∈Γ{0}such thatδα0.Then the maximal term of·cis(α0−δ)⊗⊗Then=0.This completes the proof.

Theorem 3.1Every Lie bialgebra structure on(Γ)is a coboundary triangular Lie bialgebra.

ProofSuppose that((Γ),ϕ,∆)is a Lie bialgebra structure on(Γ).Then ∆ = ∆rfor somer∈WL(Γ)⊗WL(Γ).Since Im∆⊂Im(1⊗1−τ),we geta·r∈Im(1⊗1−τ)for alla∈WL(Γ).From Lemma 3.5,we haver∈Im(1⊗1−τ),andc(r)=0 from Lemma 3.6.Thus(L,ϕ,∆)is a coboundary triangular Lie bialgebra.

4 Lie Bialgebras of Generalized Map Virasoro Algebras

In this section,we will generalize the results in Section 3 to the case of map Virasoro algebras.LetAbe a unital commutative associative algebra,such thatA⊗Ais an integral domain.We denoteWA(Γ)=W(Γ)⊗A,which is referred to as a(generalized)map Witt algebra or a(generalized)map(centerless)Virasoro algebra.In the caseA=F[t,],we get the(generalized)loop Virasoro algebras.We can write(Γ)as

with relations

Denote the twist map onA⊗Abyι(x⊗y)=y⊗x.

For an elementx∈A,we denote the left action ofxonA⊗AbyLxand the right action ofxonA⊗Aby.Explicitly,Lx(y⊗z)=(xy)⊗zand(y⊗z)=y⊗zx.Then we get two differentA-module structures onA⊗A.

LetVbe theWA(Γ)-module(Γ)⊗(Γ).As a vector space,V∼=(W⊗W)⊗(A⊗A).Explicitly,this isomorphism mapsLαx⊗yto(⊗)⊗(x⊗y).Then the action ofWL(Γ)onVis given by

Given an elementf∈(A⊗A),

The twist map ofVis given by

In a way similar to the loop case,we have the following result.

Lemma 4.1(1)The spaceDer(WA(Γ),V)can be decomposed into

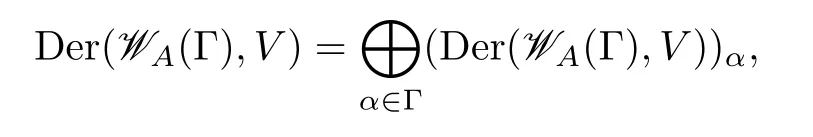
where(Der(WA(Γ),V))α⊂Inn(WA(Γ),V)for any α0.

(2)For any D∈Der(WA(Γ),V),such that D(L0)=0,we have D∈(Der(WA(Γ),V))0.

Suppose that{xi|i∈I}is a basis ofA.Then{xi⊗xj|i,j∈I}is a basis ofA⊗A.By a similar argument,we have the following lemma.

Lemma 4.2For D∈Der(WA(Γ),V),there exists a vector v∈V,such that(D−Dv)(W)=0,where Dvis defined by Dv(Lαx)=(Lαx)·v.

Now we can prove the following result.

Lemma 4.3Every derivation from WA(Γ)to V is inner,i.e.,H1(WA(Γ),V)=0.

ProofSimilarly,we take a derivationD∈(Der(WA(Γ),V))0,such thatD(W)=0.Assume thatD(Lαx)=where∈A⊗A.Obviously,=0.ApplyingDto(4.2),one has

Lettingα=β=0 in(4.6),we have

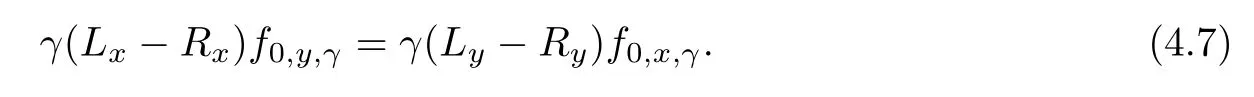
Lettingα+β=0 in(4.6),we have

Lettingx=1 andβ=0 in(4.6),we have

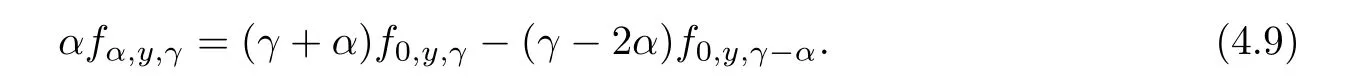
From(4.8)–(4.9),we obtain that

Ifαγ,α−γ,γ0 andxy⊗1−1⊗xy0,applyingLz−Rzto the above equation,we have

Then=0 for anyγ0.

Now we assume thatD(L0z)=for somefz∈A⊗A.ThenD(Lαz)=Lα⊗for anyα0.LettingDact on the equation=2αL0x,we havefx=0.ThusD=0.This completes the proof.

Lemma 4.4Suppose r∈V,such that a·r∈Im(1⊗1− τ)for all a∈WA(Γ).Then r∈Im(1⊗1−τ).

ProofIn a way similar to the proof of Lemma 3.5,we can taker=r0=∑wherefα∈A⊗A.LetY={α|fα0}and take someβnot belonging toY.ThenLβ·r=∑+(−α−Thus=0 andr∈Im(1⊗1−τ).This completes the proof.

In a way similar to the loop case,we can obtain the following lemma.

Lemma 4.5Suppose that c∈WA(Γ)⊗WA(Γ)⊗WA(Γ)satisfies a·c=0for all a∈WA(Γ).Then c=0.

Finally we get the main result in this section.

Theorem 4.1Every Lie bialgebra structure on WA(Γ)is a coboundary triangular Lie bialgebra.

ProofThis theorem follows from Lemmas 4.3–4.5 immediately.

[1]Allison,B.,Azam,S.,Berman,S.,et al.,Extended affine Lie algebras and their root systems,Mem.Amer.Math.Soc.,126(603),1997,x+122.

[2]Dong,C.Y.and Lepowsky,J.,Generalized Vertex Algebras and Relative Vertex Operators,Progress in Math.,Vol.112,Birkhauser,Boston,1993.

[3]Drinfeld.V.,Hamiltonian structures on Lie group,Lie algebras and the geometric meaning of classical Yang-Baxter equations,Soviet Math.Dokl,27,1983,68–71.

[4]Drinfeld.V.,Quantum groups,Proceedings of the International Congress of Mathematicians,Vol.1–2,Berkeley,Calif.1986,A.M.S.,Providence,RI,1987,798–820.

[5]Farnsteiner,R.,Derivations and central extensions of finitely generated graded Lie algebras,J.Algebra,118,1988,33–45.

[6]Kac,V.G.,Infinite-Dimensional Lie Algebras,Cambridge University Press,Cambridge,1990.

[7]Guo,X.Q.,Lu,R.C.and Zhao,K.M.,Simple Harish-Chandra modules,intermediate series modules,and Verma modules over the loop-Virasoro algebra,Forum Math.,23,2011,1029–1052.

[8]Ng,S.H.and Taft,E.J.,Classification of the Lie bialgebra structures on the Witt and Virasoro algebras,J.Pure Appl.Algebra,151,2000,67–88.

[9]Savage,A.,Classification of irreducible quasifinite modules over map Virasoro algebras,Transform.Groups,17,2012,547–570.

[10]Song,G.A.and Su,Y.C.,Lie bialgebras of generalized Witt type,Science in China,Ser.A,49,2006,533–544.

[11]Song,G.A.and Su,Y.C.,Dual Lie bialgebras of Witt and Virasoro types,to appear.arXiv:1306.0781

[12]Su,Y.C.,Harish-Chandra modules of intermediate series over the high rank Virasoro algebras and high rank super-Virasoro algebras,J.Math.Phys.,35,1994,2013–2023.

[13]Su,Y.C.,Classification of Harish-Chandra modules over the super-Virasoro algebras,Comm.Algebra,23,1995,3653–3675.

[14]Su,Y.C.,Simple modules over the higher rank super-Virasoro algebras,Lett.Math.Phys.,53,2000,263–272.

[15]Su,Y.C.,Simple modules over the high rank Virasoro algebras,Comm.Algebra,29,2001,2067–2080.

[16]Su,Y.C.,Classification of Harish-Chandra modules over the higher rank Virasoro algebras,Comm.Math.Phys.,240,2003,539–551.

[17]Su,Y.C.,Wu,H.N.,Wang,S.and Yue,X.Q.,Structures of generalized map Virasoro algebras,Symmetries and Groups in Contemporary Physics,505–510,Proceedings of the XXIX International Colloquium on Group-Theoretical Methods in Physics(Tianjin,China,August 20–26,2012),World Scientific,Singapore,2013.

[18]Su,Y.C.,Xu,X.P.and Zhang,H.C.,Derivation-simple algebras and the structures of Lie algebras of Witt type,J.Algebra,233,2000,642–662.

[19]Su,Y.C.and Zhao,K.M.,Second cohomology group of generalized Witt type Lie algebras and certain representations,Comm.Algebra,30,2002,3285–3309.

[20]Taft,E.J.,Witt and Virasoro algebras as Lie bialgebras,J.Pure Appl.Algebra,87,1993,301–312.

[21]Wu,H.N.,Wang,S.and Yue,X.Q.,Structures of generalized loop Virasoro algebras,Comm.Algebra,42,2014,1545–1558.

[22]Yue,X.Q.and Su,Y.C.,Lie bialgebra structures on Lie algebras of generalized Weyl type,Comm.Algebra,36,2008,1537–1549.