Vertex Representations of Toroidal Special Linear Lie Superalgebras∗

Naihuan JING Chongbin XU

1 Introduction

Let g be a finite-dimensional simple Lie(super)algebra of typeXandRbe the ring of Laurent polynomials in commuting variables,and then the toroidal Lie(super)algebraT(g)is by definition the perfect central extension of the loop algebra g⊗R.WhenR=C[t,t−1],the toroidal Lie algebra is the affine Kac-Moody Lie algebra.The larger class of Lie(super)algebrasT(g)shares many properties with the untwisted affine Lie(super)algebras.

In the case of untwisted toroidal Lie algebras,Moody,Rao and Yokonuma[18]gave a loop algebra presentation for the 2-toroidal Lie algebras similar to the affine Kac-Moody Lie algebras,which has set the stage for later developments such as free field realizations and vertex operator representations.Notably in[20]the toroidal Lie algebras of typeBnwere constructed by using fermionic operators(see[8]).On the other hand,level-one representations of toroidal Lie algebras of the simply laced types were realized via McKay correspondence and wreath products of Kleinian subgroups ofSL2(C)(see[5]).Bosonic realizations of higher-level toroidal Lie algebrasT(A1)were also given in[10].More recently,a unified realization(see[9,11])of all 2-toroidal Lie algebras of classical types was constructed by using bosonic or ferminoic fields,which has generalized the Feingold-Frenkel construction(see[4])for affine Lie algebras.

Affine Lie superalgebras have been studied as early as their non-super counterparts.In fact,Feingold and Frenkel construction works for Lie superalgebras as well(see[4]).Vertex superalgebras and their representations were also given in[15].Later in[14]integrable highestweight modules were constructed for affine superalgebras of the orthosymplectic seises using fermionic and bosonic fields.All these constructions were based on the loop algebra realizations of affine Lie superalgebras.

Irreducible highest-weight modules of classical toroidal Lie superalgebras can be constructed abstractly as in the affine cases(see[19]).Various other constructions of toroidal Lie superalgebras and their generalizations were known(see[1,3,9,16–17]).In particular,[2]has constructed a certain vertex operator representation for the general toroidal cases.Recently we have given a loop algebra realization for 2-toroidal classical superalgebras(see[12]),which is a super analog of the MRY construction(see[7]for earlier development).

The aim of this work is to generalize Kac and Wakimoto’s work on affine superalgebras of unitary series to the 2-toroidal setting using both vertex operators and Weyl bosonic fields,and the construction has utilized our recent MRY presentation exclusively.We remark that our work is different from[2]in that we use more bosonic fields while the latter used more vertex operators.This suggests that there could be a super boson-fermion correspondence for the 2-toroidal cases.

This paper is organized as follows.In Section 2 we recall the notions of 2-toroidal Lie superalgebras and the loop-algebra presentation.In Section 3 we construct certain vertex operators and Weyl bosonic fields to give a level-one representation of the 2-toroidal Lie special linear superalgebra.

2 The Toroidal Lie Superalgebra T(A(m,n))

LetV=be the Z2-graded vector space of dimension(m,n+1),wheremn.Let gl(m|n+1)be the Lie superalgebra of the super-endomorphisms ofVunder the superbracket.Let g be the traceless subalgebra,i.e.,the simple Lie superalgebra of typeA(m,n).LetR=be the complex commutative ring of Laurant polynomials ins,t.The loop Lie superalgebraL(g):=g⊗Ris defined under the Lie superbracket[x⊗a,y⊗b]=[x,y]⊗ab.

Let ΩRbe theR-module of Khler differentials{bda|a,b∈R},and letdΩRbe the space of exact forms.The quotient space ΩR/dΩRhas a basis consisting ofwherem,n∈Z.Heredenotes the coseta+dΩR.

The toroidal special linear superalgebraT(g)is defined to be the Lie superalgebra on the following vector space:

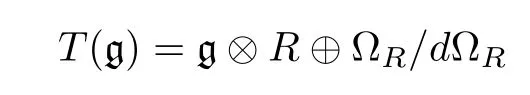
with the Lie superbracket(x,y∈g,a,b∈R):

and the parities are specified by:

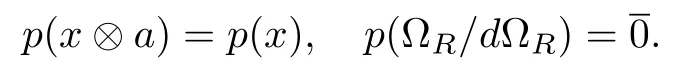
LetA=)be the extended distinguished Cartan matrix of the affine Lie superalgebra of typeA(m,n),i.e.,

and letQ=Zα0⊕···⊕Zbe its root lattice.Hereα0,are the odd simple roots.The standard invariant form is given by()=,where(,···,)=

We recall the loop algebra presentation of the 2-toroidal Lie superalgebras.

Theorem 2.1(see[12])The toroidal special linear superalgebra T(g)is isomorphic to the Lie superalgebraT(A(m,n))generated by

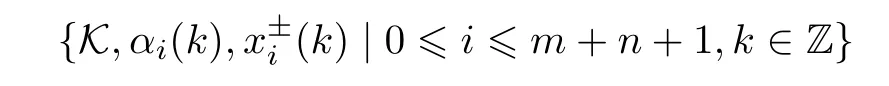
with parities given as

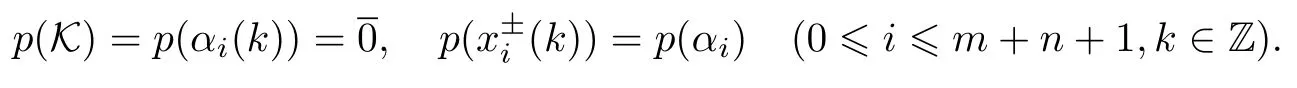
The defining relations of superbrackets are given by:

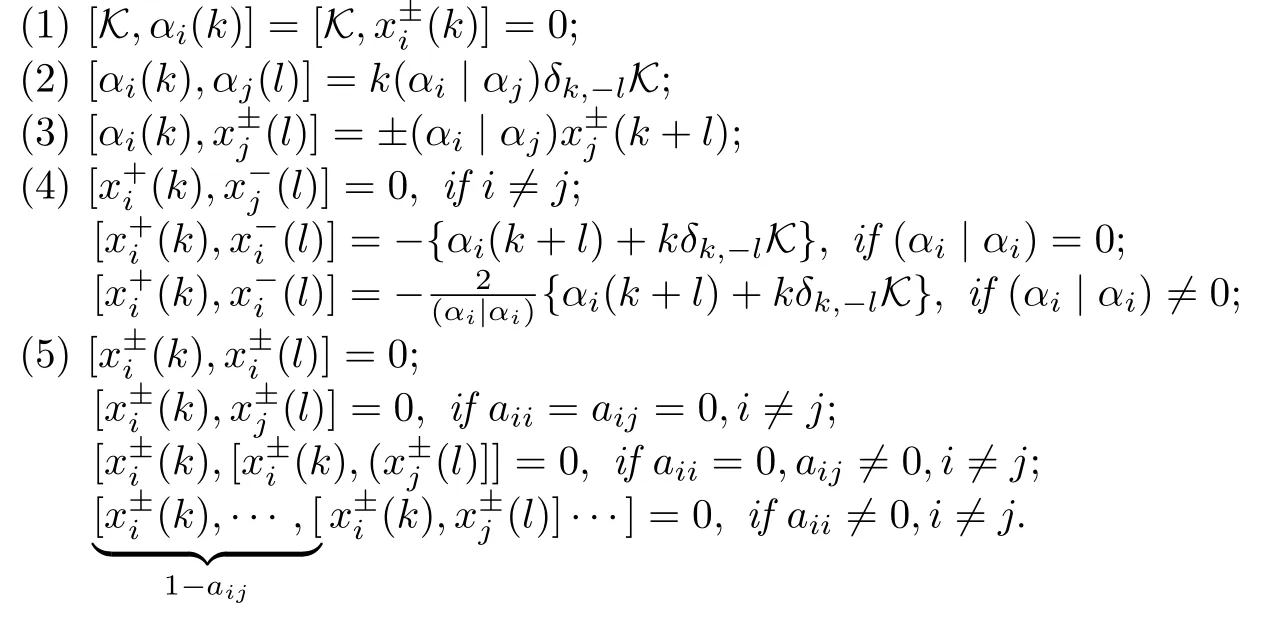
We define the formal power series with coefficients from T(A(m,n)):

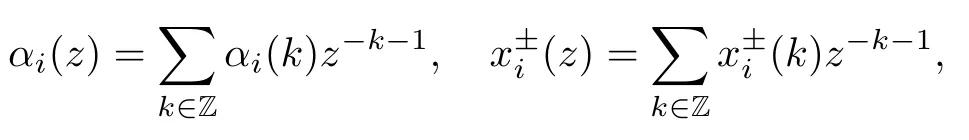
and then the defining relations of T(A(m,n))can be rewritten in terms of the formal series as follows.

Proposition 2.1The relations ofT(A(m,n))can be written as follows:

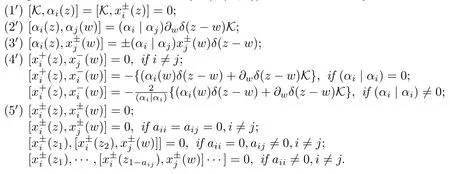
Here we have used the formal delta function

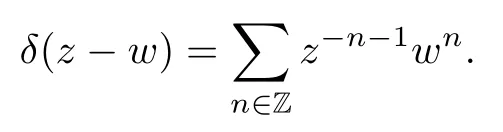
Its derivatives are given by the power series expansions(see[13]):

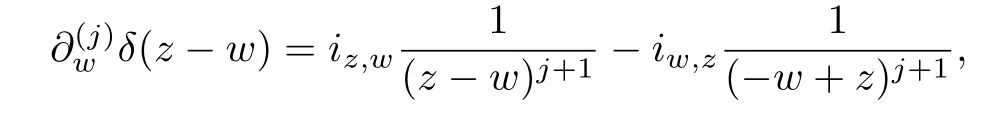
whereandmeans power series expansion in the domain|z|>|w|.By convention,if we write a rational function in the variablez−w,it is usually assumed that the power series is expanded in the region|z|>|w|.Finally,the equation

holds when both sides are meaningful.

3 The Vertex Representation of T(A(m,n))

In this section,we will give a representation of the Lie superalgebra T(A(m,n))using both vertex operators and bosonic fields.

Let(0 6i6n+m+3)be an orthomormal basis of the vector spaceand denote=(1 6i6n+2).Then the distinguished simple root systems,the positive root systems and the longest distinguished root of the Lie superalgebra of typeA(m,n)can be represented in terms of vectors’s and’s as follows:

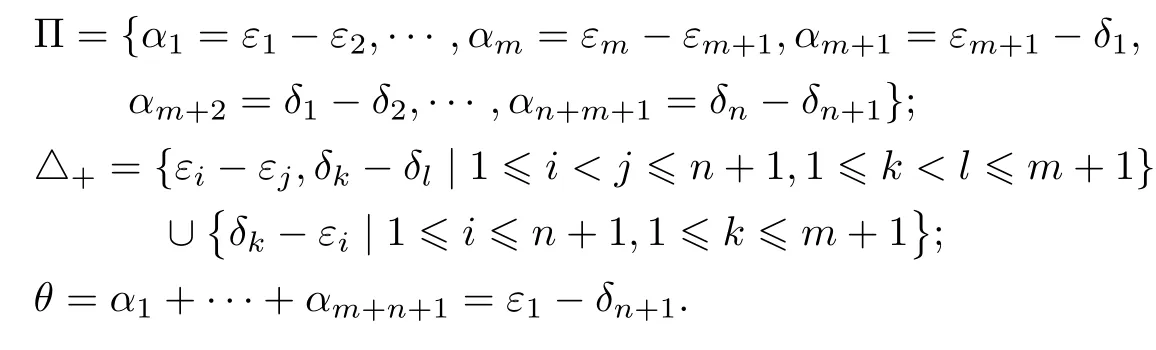
3.1 Vertex operators

Let Γ =Z⊕···⊕and h= ΓC.We view h as an abelian Lie algebra and consider the central extension of its affinization,i.e.,

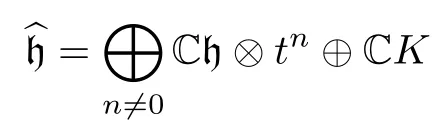
with the following communication relations:

whereα(k)=α⊗andα,β∈Γ;k,l∈Z.This is an infinite-dimensional Heisenberg algebra.

Fori=0,1,we let{α∈Γ|(α,α)∈2Z+i},so then Γ =LetF:Γ×Γ→{±1}is the bimultiplicative map determined by

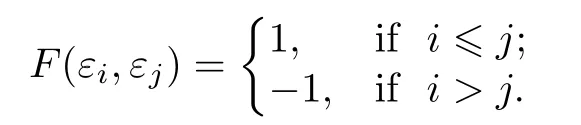
Then the map satisfies the following properties:

Let C[Γ]be the vector space spanned by the basis{|γ∈Γ}over C.We define a twisted group algebra structure on C[Γ]as follows:

We form the tensor space

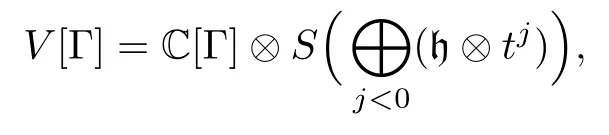
and define the action ofas follows:Kacts as the identity operator,α(−k)(k>0)acts as multiplication byα⊗forα∈Γ,andα(k)(k>0)acts as the derivation ofV[Γ]defined by the formula

The spaceV[Γ]has a natural Z2-gradation:V[Γ]=V[Γ⊕V[ΓwhereV[Γ(resp.V[Γis the vector space spanned by⊗β⊗withα,β∈Γ;j∈Z+such that(α,α)∈2Z(resp.(α,α)∈2Z+1).

Forα∈Γ,we define the vertex operatorY(α,z)as follows:

where the operatoris given by

forβ,γ∈Γ;j∈Z+and we denote

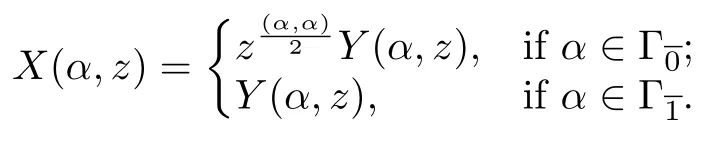
We expandX(α,z)inz

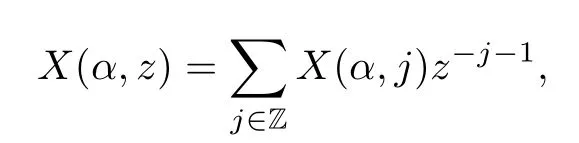
where the componentsX(α,j)are well-defined local operators.Similarly,forα∈Γ,we define

Lemma 3.1For α∈β∈one has that

ProofThe first and second parts have been proved in[1].For the third part,we refer to[21].

Corollary 3.1(1)[X(εi,z),X(εj−εk,w)]=δikF(εi,εj−εk)X(εj,w)δ(z−w),jk;

(2)[X(εi,z),X(−εj,w)]=δijF(εi,−εj)∂wδ(z−w);

(3)[α(z),X(β,w)]=(α,β)X(β,z)δ(z−w),α,β∈Γ.

ProofThe corollary is a direct consequence of Lemma 3.1.

3.2 Bosonic fields

We introduceand defineβ=so thenα0=Note that(β|β)=−1,=LetPbe the vector spaces spanned by the set1 6i6n+1}andP∗be its dual space.LetC=P⊕P∗and define the bilinear form on it as follows:Fora,b∈P,

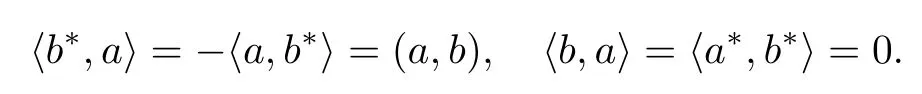
Letbe the Weyl algebra generated by{u(k)|u∈C,k∈Z}with the defining relations

foru,v∈Candk,l∈Z.

The representation space of the algebrasA()is defined to be the following vector space:

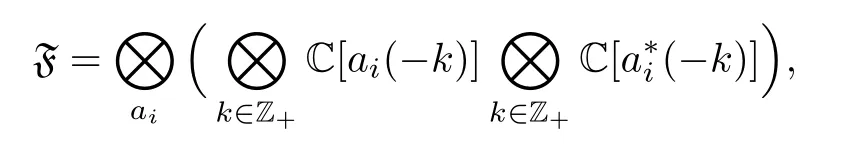
whereairuns through any basis inP,consisting ofand’s.The algebraacts on the space by the usual action:a(−k)acts as creation operators anda(k)as annihilation operators.

Foru∈C,we define the formal power series with coefficients from the associative algebraA():

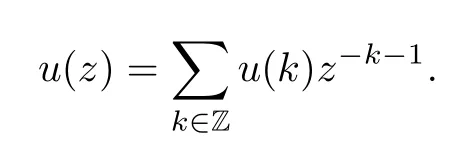
It is a bosonic field acting on the Fock space F.

In the following,we will give a representation of T(A(m,n))on a quotient V of the tensor spaceV[Γ]⊗F:

Therefore,the relation::=0 holds on V.Note that there is a natural homomorphism from V ontoV]⊗,whereFor simplicity,we will use the same symbol to denote the coset elements in V.Observe that there is a Z2-gra tion on this space with the parity given byp(eα⊗x⊗y)=p(α)forα∈Γ,x∈S(⊕y∈F.The vertex operatorsX(α,z),α(z)act on the first component and the bosonic fieldu(z)acts on the second component.It follows that

For any two fieldsa(z),b(w)with fixed parity,we define the normal ordered product by

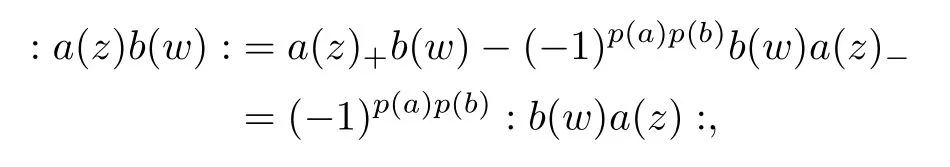
wherea±(z)is defined as usual.Based on the normal ordering of two fields,one can define inductively the normal ordering of more than two fields “from right to left”.

The following facts are well known in literature(see[6,11]).

Proposition 3.1One has that

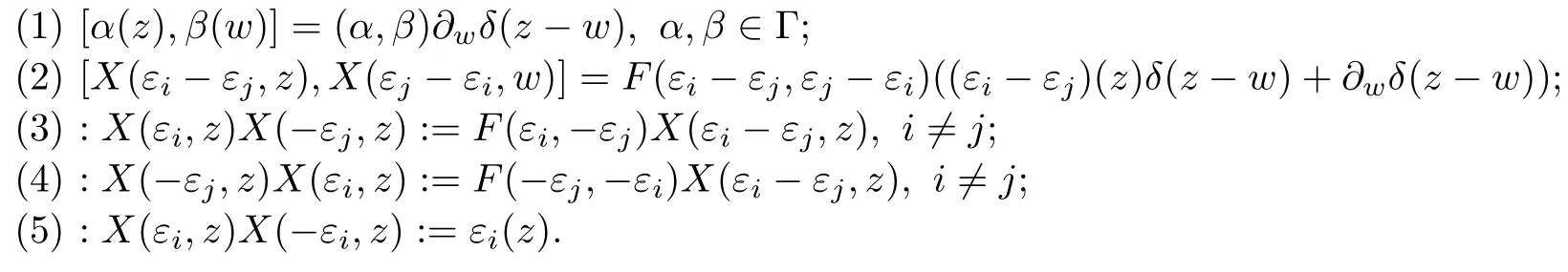
Furthermore,we define the contraction of two fieldsa(z),b(w)by

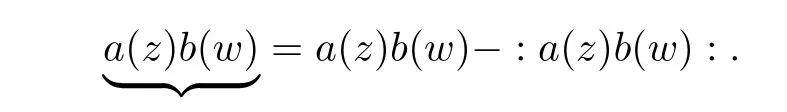
Proposition 3.2(see[13])Suppose that fields a(z),b(w)satisfy the following equality:

where N is a positive integer and cj(w)are formal distributions in the indeterminate z,and then we have that

The following well-known Wick’s theorem is useful for calculating the operator product expansions(OPE)of normally ordered products of free fields.

Theorem 3.1(see[13])Let A1,A2,···,and ,,···,be two collections of fi elds with definite parity.Suppose that these fields satisfy the following properties:

Then we have that

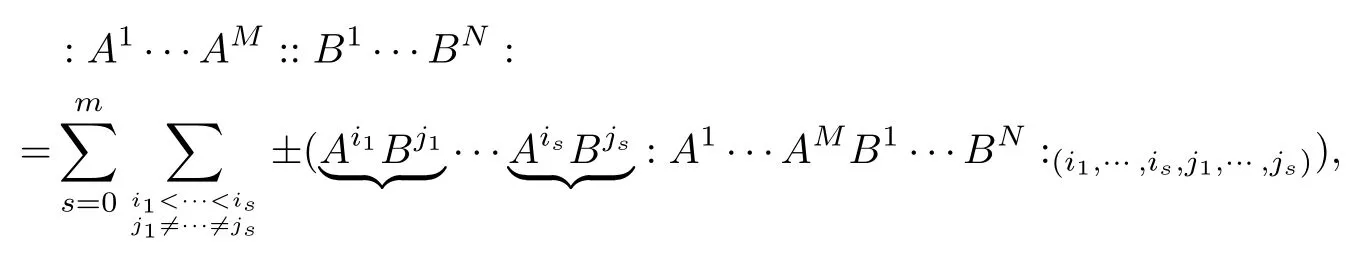
where m=min{M,N}and the subscript(,···,,,···,)means that the fields ,...,,,...,are removed and the sign±is obtained by the rule:Each permutation of the adjacent odd fields changes the sign.

Now we state the main result of this paper.

Theorem 3.2The following map defines a level-one representation on the spaceV:

ProofTo prove the theorem,one needs to check that all the field operators on the right side of above map satisfy relations(–(listed in Proposition 2.1.

First of all,we check()–()with the help of Wick’s theorem.

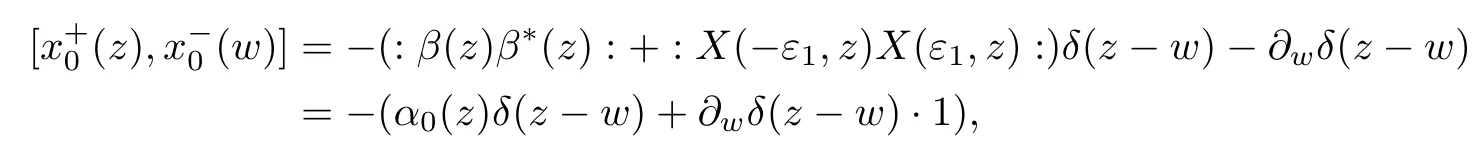
where we have used the fact::=−(z)and

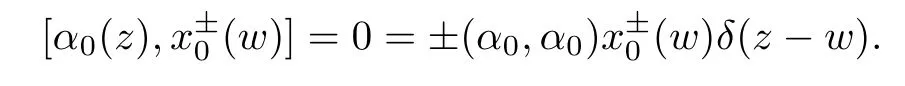
For 1im,we have by Proposition 3.1 that

It follows from Corollary 3.1 that

and

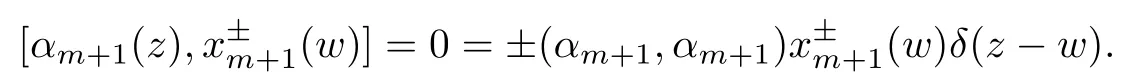
Form+2im+n+1,we have that

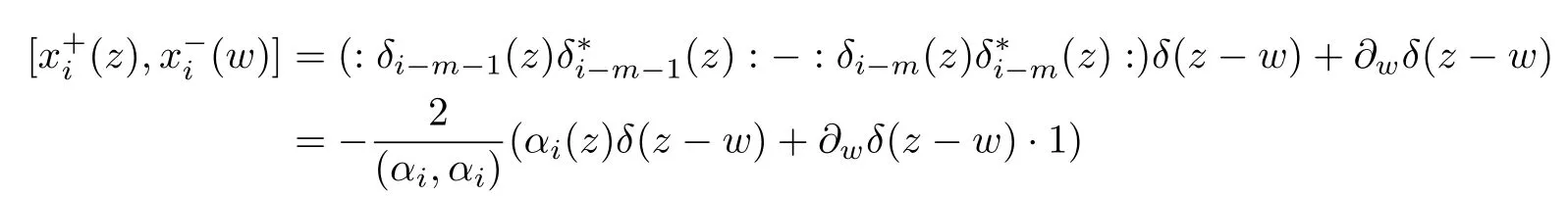
and

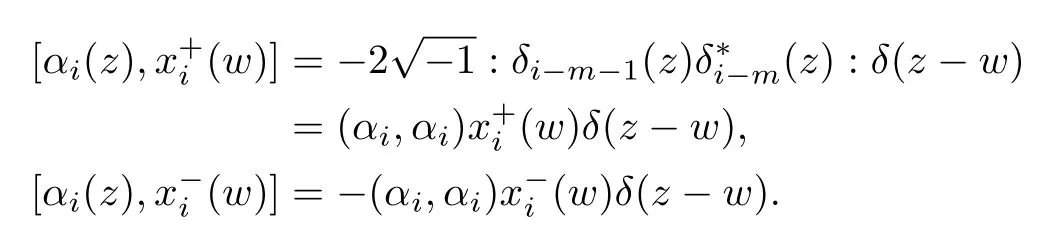
For allij,we have=0 and for any disconnected vertices

All the rest can be checked by straightforward calculation,for example,

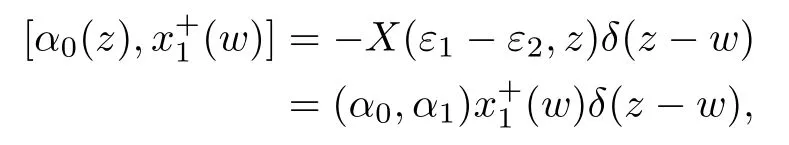
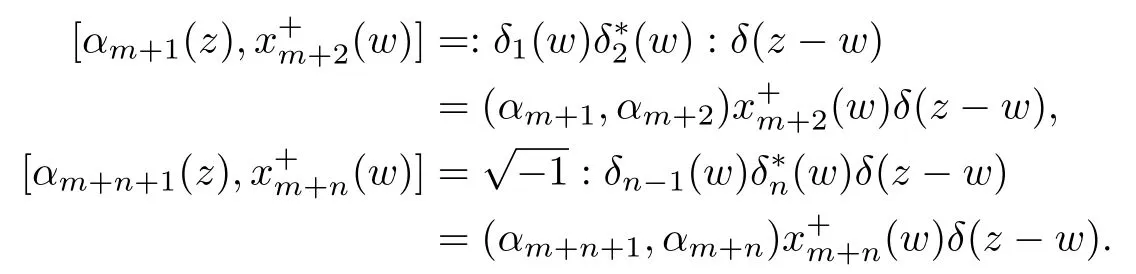
For the extremal vertices,one also has that

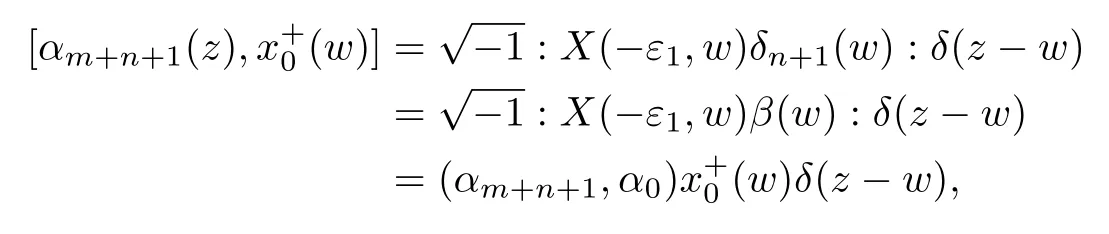
where we have used the fact that

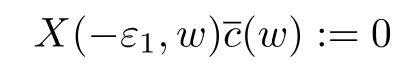
and others can be proved similarly.

Secondly,we can check(2′)case by case by using Proposition 3.1(1)and we include the following examples:

Finally,we proceed to check the Serre relations.It is easy to verify that=0 for 0im+n+1 and=0 forij,=0.The rest can be checked directly:

The remaining relations follow similarly by Wick’s theorem or Corollary 3.1.This completes the proof of the theorem.

AcknowledgmentsThe authors thank the referee for his/her suggestions which have helped to improve the paper greatly.Many thanks also go to the editors of CAM for their help in the submission process of this paper.

[1]Bhargava,S.,Chen,H.and Gao,Y.,A family of representations of the Lie superalgebraJ.Alg.,386,2013,61–76.

[2]Eswara Rao,S.,Representation of toroidal general linear superalgebras,Commun.Alg.,42,2013,2476–2507.

[3]Eswara Rao,S.and Moody,R.V.,Vertex representations for N-toroidal Lie algebras and a generalization of the Virasoro algebra,Commun.Math.Phys.,159,1994,239–264.

[4]Feingold,A.J.and Frenkel,I.B.,Classical affine algebras,Adv.Math.,56,1985,117–172.

[5]Frenkel,I.B.,Jing,N.and Wang,W.,Vertex representations via finite groups and the MaKay correspondence,Int.Math.Res.Notices,4,2000,195–222.

[6]Frenkel,I.B.,Lepowsky,J.and Meuraman,A.,Vertex Operator Algebras and the Monster,Academic Press,Boston,1988.

[7]Iohara,K.and Koga,Y.,Central extensions of Lie superalgebras,Commun.Math.Helv.,76,2001,110–154.

[8]Jiang,C.and Meng,D.,Vertex representations for theν+1-toroidal Lie algebra of typeBl,J.Alg.,246,2001,564–593.

[9]Jing,N.and Misra,K.C.,Fermionic realization of toroidal Lie algebras of classical types,J.Alg.,324,2010,183–194.

[10]Jing,N.,Misra,K.C.and Tan,S.,Bosonic realizations of higher level toroidal Lie algebras,Pacific J.Math.,219,2005,285–302.

[11]Jing,N.,Misra,K.C.and Xu,C.,Bosonic realization of toroidal Lie algebras of classical types,Proc.AMS,137,2009,3609–3618.

[12]Jing,N.and Xu,C.,Toroidal Lie superalgebras and free field representations,Contemp.Math.,623,2014,135–153.

[13]Kac,V.G.,Vertex Algebras for Beginners,Univ.Lect.Ser.,10,AMS,Providence,1997.

[14]Kac,V.G.and Wakimoto,M.,Integrable highest weight modules over affine superalgebras and Appell’s function,Commun.Math.Phys.,215,2001,631–682.

[15]Kac,V.G.and Wang,W.,Vertex operator superalgebras and their representations,Contemp.Math.,175,1994,161–191.

[16]Lau,M.,Representations of multiloop algebras,Pacific J.Math.,245,2010,167–184.

[17]Liu,D.and Hu,N.,Vertex representations for toroidal Lie algebra of typeG,J.Pure Appl.Alg.,198,2005,257–279.

[18]Moody,R.V.,Rao,S.E.and Yokonuma,T.,Toroidal Lie algebras and vertex representations,Geom.Ded.,35,1990,283–307.

[19]Rao,S.E.and Zhao,K.,On integrable representations for toroidal Lie superalgebras,Contemp.Math.,343,2004,243–261.

[20]Tan,S.,Vertex operator representations for toroidal Lie algebra of typeBl,Commun.Alg.,27,1999,3593–3618.

[21]Xu,X.,Introduction to Vertex Operator Superalgebras and Their Modules,Kluwer Academic Publishers,Dordrecht,1998.