Asymptotic Stability of Equilibrium State to the Mixed Initial-Boundary Value Problem for Quasilinear Hyperbolic Systems∗

Yanzhao LI Cunming LIU

1 Introduction and Main Results

Consider the following first-order quasilinear hyperbolic system:

whereu=(u1,···,un)Tis the unknown vector function of(t,x),A(u)=((u))is aC2matrix function ofu,andF(u)=(F1(u),···,Fn(u))Tis aC2vector function ofuwith

By strict hyperbolicity,for any givenuon the domain under consideration,A(u)hasndistinct real eigenvaluesλ1(u)<···<λn(u)and a complete set of left(resp.right)eigenvectorsli(u)=(li1(u),···,lin(u))(resp.ri(u)=(r1i(u),···,rni(u))T)as follows:

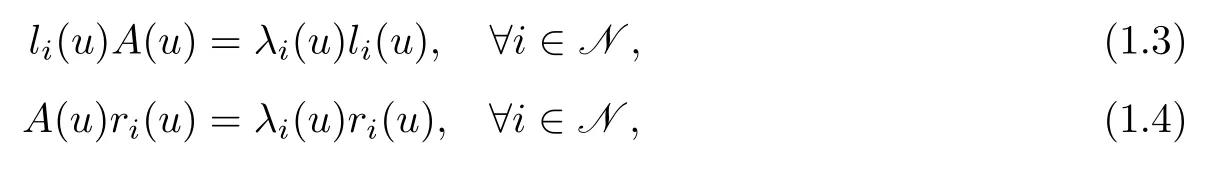
where

Assume thatλi(u),li(u)andri(u)(i∈N)have the same regularity asA(u).Without loss of generality,we assume that

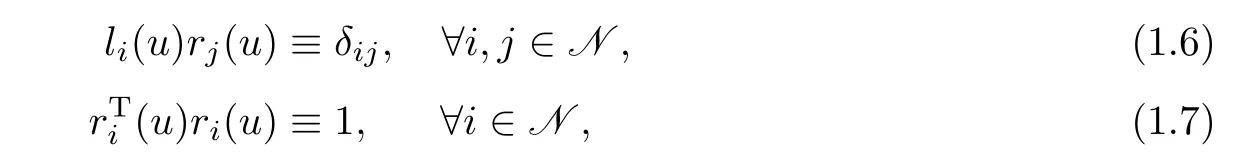
whereδijstands for the Kronecker symbol.LetL(u)andR(u)be the matrices composed of the left and right eigenvectors:

respectively.

In order to consider the mixed initial-boundary value problem for(1.1),assume that there exists an indexm∈{1,···,n−1},such that

Remark 1.1Foru=(u1,···,un)T∈Rn,denote

LetMn,nbe the set ofn×nreal matrices,andDn,nbe the set ofn×nreal diagonal matrices with strictly positive diagonal elements.For any givenB=(bij)∈Mn,n,we define

If(1.1)satisfies the following internal dissipative condition:There exists Λ∈Dn,n,such that

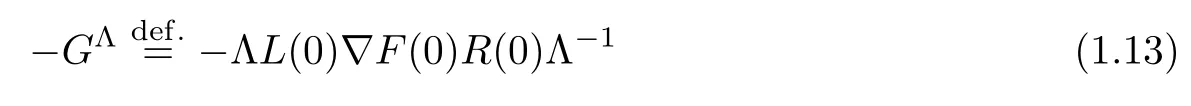
is a strictly row-diagonal dominant matrix as follows:

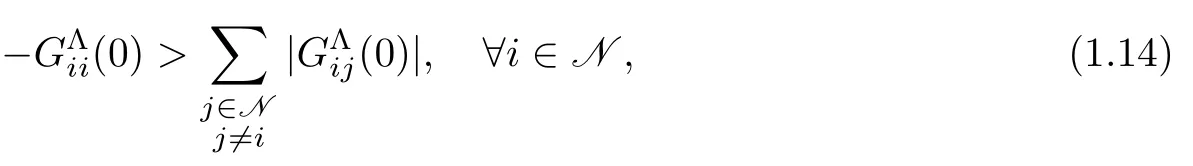
then the Cauchy problem for(1.1)admits a unique globalC1solutionu=u(t,x)ont≥0,and theC1norm ofudecays exponentially to zero ast→+∞,provided that theC1norm of the initial data is small enough(see[6–7]).By the method of energy integration,[5]gave the global existence and uniqueness ofH2solutions to the hyperbolic system of conservation laws with small initial data under the Shizuta-Kawashima condition and the entropy dissipative condition,and then this result was reproved in[16]in a different way under slightly different hypotheses.The generalization to the higher dimensional case can be found in[15],and[1–2]gave the corresponding asymptotic behavior.Moreover,this result was generalized to some systems without the Shizuta-Kawashima condition in[11–14].

Consider the mixed initial-boundary value problem(1.1)with the initial condition

and the following boundary conditions:

wherevi=li(u)u(i∈N),HrandHs(r=1,···,m,s=m+1,···,n)areC2functions of(vm+1,···,vn)Tand(v1,···,vm)T,respectively,and

Assume that the conditions ofC1compatibility hold at the points(0,0)and(0,1),respectively.

IfF(u)satisfies(1.2)and

and the matrix

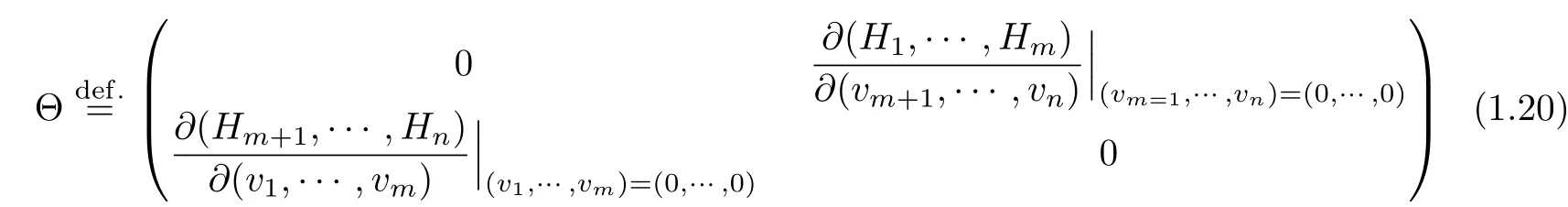
satisfies the following boundary dissipative condition:

then the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)with small initial data admits a unique globalC1solutionu=u(t,x)on the domain{(t,x)|t≥0,0≤x≤1},and theC1norm of the solution decays exponentially ast→+∞(see[7]).In the caseF(u)≡0,by constructing a Lyapunov function and considering the problem inH2space,the condition(1.21)is weakened in[3].For linear hyperbolic systems,the exponential stability for the mixed initial-boundary value problem was established inL2space in[4].

The results mentioned above inspire us to consider the following problem:In the case∇F(0)0,under what conditions on∇F(0)and Θ,i.e.,under which kind of combined effect of internal dissipation and boundary dissipation,we can get the global existence and the exponential decay of theC1solution to the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)?

Let

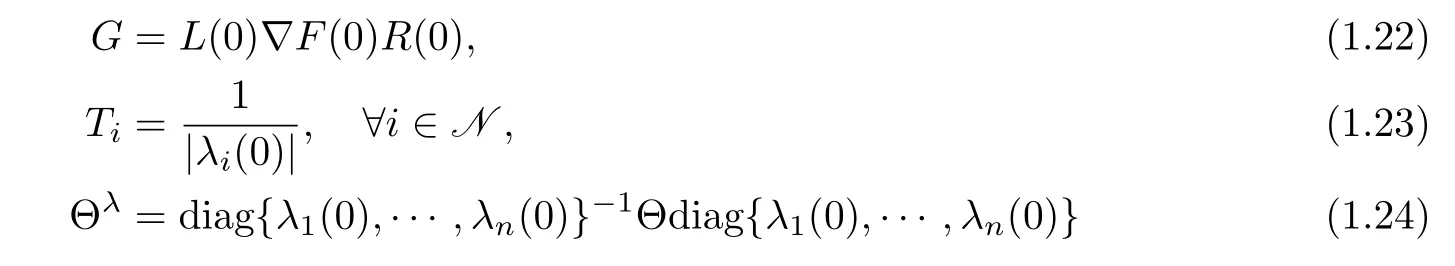
and

Our main result is as follows.

Theorem 1.1Under the hypotheses(1.2),(1.10)and(1.18),assume furthermore that0(i∈N).If G,Θ,Θλsatisfy

then there exists ε0>0so small that for any given ε∈[0,ε0]and the initial data u0(x)satisfying(1.25),the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)admits a unique global C1solution u=u(t,x)on the domain{(t,x)|t≥0,0≤x≤1},and there exists a number α>0,such that for any given t≥0,we have the following uniform a priori estimate:

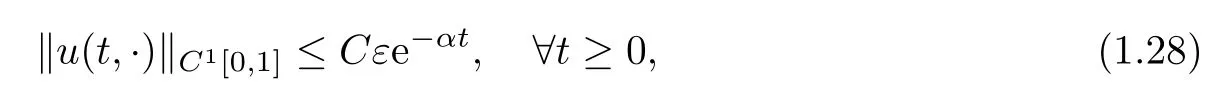
where C stands for a positive constant independent of ε and t.

Remark 1.2IfGii=0(i∈N),(1.26)–(1.27)should be replaced by

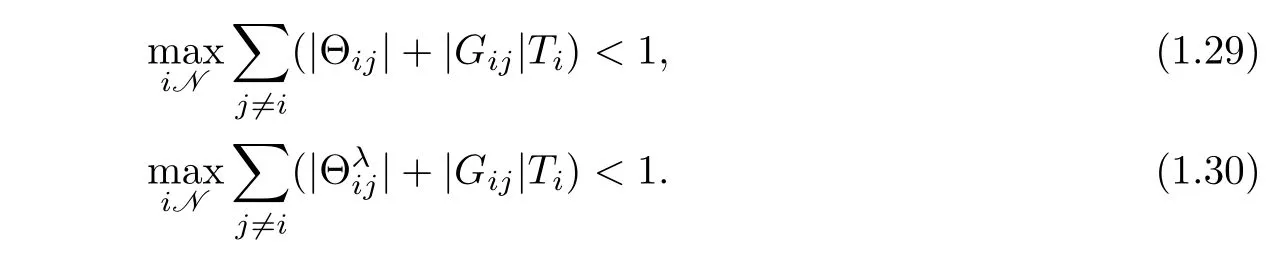
Through the proof in Section 3,we can see that Theorem 1.1 still holds in this case.In order to get(1.29)–(1.30),we may use the Taylor expansion ofin(1.26)–(1.27),and then askto tend to 0.

Generally speaking,if there exists a setP1⊆N,such thatGkk=0,∀k∈P1,then Theorem 1.1 still holds,provided that(1.26)–(1.27)are replaced by

Remark 1.3If there exist Λ and ∆∈Dn,n,such that

and

satisfy(1.26),while

and

satisfy(1.27),then the conclusion of Theorem 1.1 still holds.Remark 1.4When

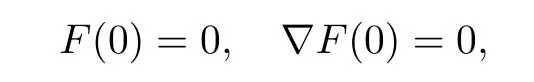
namely,there do not exist any linear internal dissipative terms,through the proof and analysis in Section 3,(1.26)–(1.27)can be reduced to(1.21),and then the result in[7]can be obtained from the conclusion of Theorem 1.1.

When

namely,there do not exist any linear boundary dissipative terms,in order to get(1.26)–(1.27),the nonlinear termF(u)of(1.1)might have a growth effect on the solutionu=u(t,x)(i.e.,Gii>0).Specially,taking

we can see it.

Remark 1.5(1.14)fails for some systems in physics,however,it is possible to get

If

and

then(1.26)–(1.27)still hold.By Theorem 1.1,theC1solution to the corresponding mixed initial-boundary value problem decays exponentially.

In Section 2,we give the semi-global existence of aC1solution to the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)(see[8]),and a kind of formulas of wave decomposition.By using these formulas,we give the proof of Theorem 1.1 in Section 3,and we apply our result to a kind of models in Section 4.In Section 5,one example is given to show that the conclusion of Theorem 1.1 may fail if(1.26)–(1.27)do not hold,and some further discussions about our main results are carried out in Section 6.

2 Preliminaries

Under hypotheses(1.2),(1.10)and(1.18),there existst∗>0,such that the mixed initialboundary value problem(1.1)and(1.15)–(1.17)admits a uniqueC1solutionu=u(t,x)on the domain{(t,x)|0≤t≤t∗,0≤x≤1}(see[10]).In order to prove Theorem 1.1,we first give the semi-global existence of aC1solution to the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)(see[8])and some formulas of wave decomposition in this section.

Lemma 2.1Suppose that(1.2),(1.10)and(1.18)hold.For any given T>0,there exists an ε0>0so small that for any given ε∈[0,ε0]and u0(x)satisfying(1.25),the mixed initialboundary value problem(1.1)and(1.15)–(1.17)admits a unique C1solution u=u(t,x)on the domain

and satisfies

where C is a positive constant independent of t∈[0,T]and ε∈[0,ε0].

2.1 Formulas of wave decomposition

In order to prove Theorem 1.1,we introduce some formulas of wave decomposition.

Let

Then

By(1.1),we have

where

and

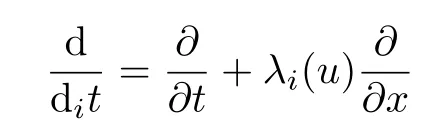
denotes the directional derivative with respect totalong theith characteristic curve(see[7]).

Similarly,by(1.1)we have

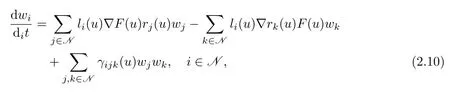
where

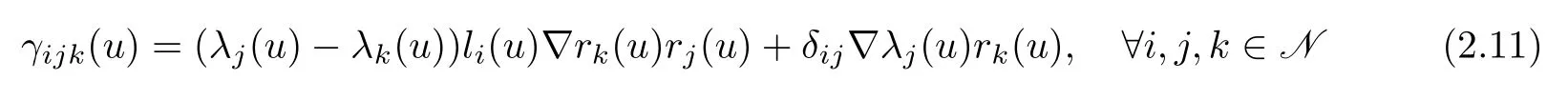
(see[7]).

Noting(1.2)and(2.3),we have

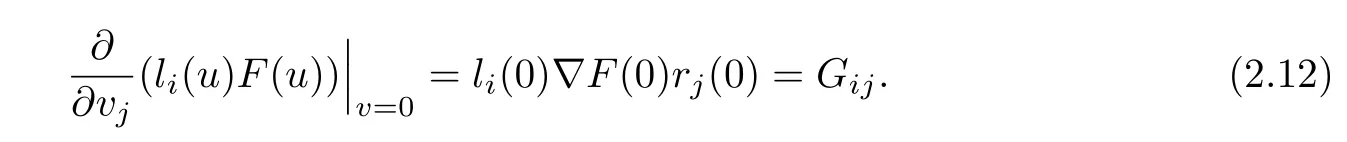
Thus,using Hadamard’s formula and Taylor expansion for functionsli(u)F(u),we have

whereIn a similar way,by(1.2),for functionswe have

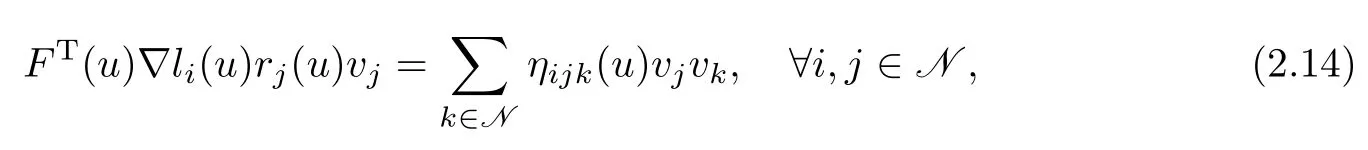
where

Similarly,we have

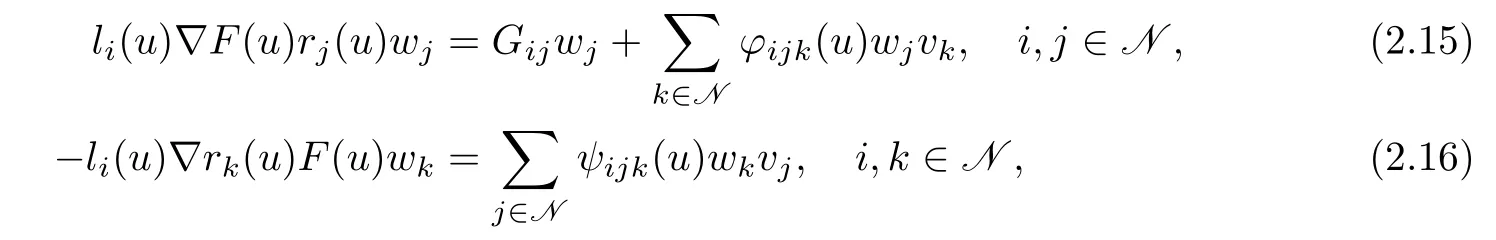
where(i,j,k∈N).Substituting(2.13)–(2.14)and(2.15)–(2.16)into(2.8)and(2.10),respectively,we get

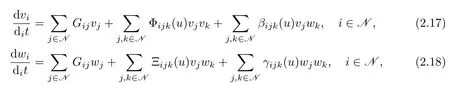
where∈C0(i,j,k∈N)are given by

2.2 Representation of v and w on the boundaries x=0,1

Noting(1.18)and(1.20),it follows from boundary conditions(1.16)–(1.17)that

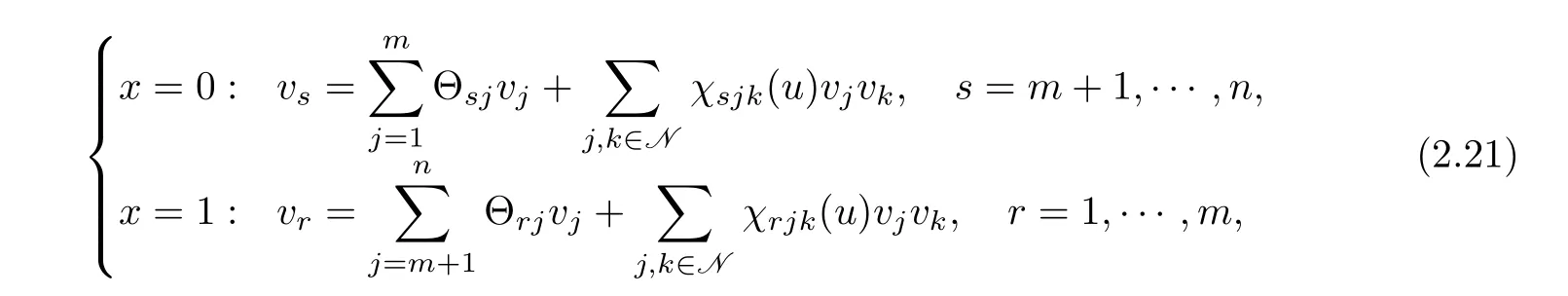
where(u)∈C0(i,j,k∈N).

Differentiating the boundary conditions(1.16)–(1.17)with respect totyields

For any giveni∈N,by(2.3)–(2.4)and(2.13)–(2.14),we have

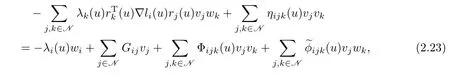
where

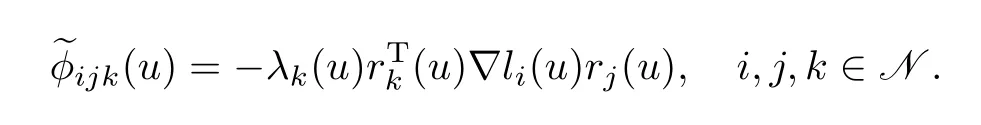
Substituting(2.23)into(2.22),we get

For the functions(s=m+1,···,n;r=1,···,m)and(s=m+1,···,n;r=1,···,m)appearing on the right-hand side of(2.24),using Taylor expansion,we obtain

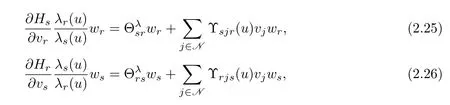
whereis given by(1.24).Substituting(2.25)–(2.26)into(2.24),

we get

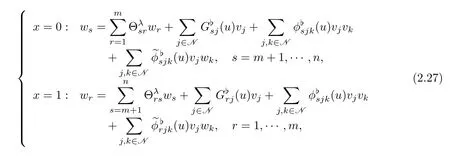
where

Remark 2.1Noting that the coefficient matrixGappearing on the right-hand side of(2.17)forv=(v1,···,)Tis the same as that of(2.18)forw=but the coefficient matrix Θ appearing on the right-hand side of(2.21)forv=is different fromof(2.27)forw=(w1,···,Thus,for any given Λ =diag{Λ11,···,and ∆ =diag{,···,using the following linear transformations forv=andw=(w1,···,wn)T:

the corresponding coefficient matrices of(2.17)–(2.18)are

respectively,while the corresponding coefficient matrices of(2.21)and(2.27)are

respectively.Therefore,(1.26)–(1.27)in Theorem 1.1 should be satisfied at the same time.

3 Proof of Theorem 1.1

On any given existence domainD(T)of theC1solutionu=u(t,x)to the mixed initialboundary value problem(1.1)and(1.15)–(1.17),assume that

and

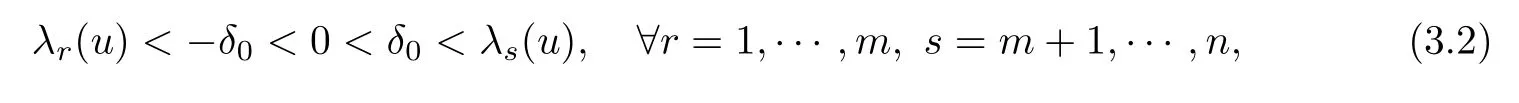
whereδandδ0are positive constants independent ofεandT.Noting(1.26)–(1.27)and the continuity,there existsα>0,such that

Noting(3.1),the functions(i,j,k∈N)appearing on the right-hand sides of(2.17)–(2.18)and(2.27)are all bounded,so then there exists a constantM≫1,such that

Let

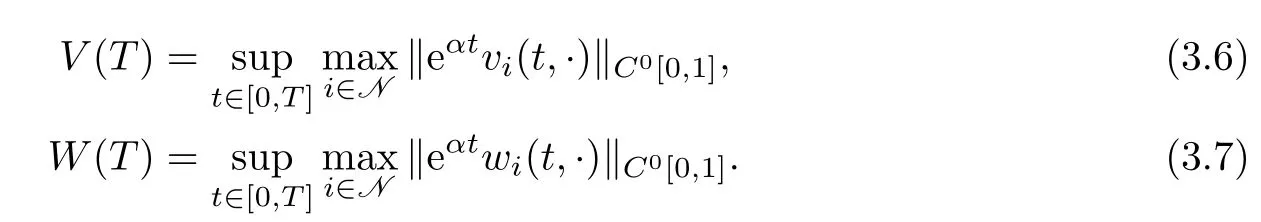
To prove Theorem 1.1,we only need to prove that on any given existence domainD(T)of theC1solutionu=u(t,x)to the mixed initial-boundary value problem(1.1)and(1.15)–(1.17),we have

whereC1andC2are positive constants large enough,independent ofεandT,to be specified later on.

By Lemma 2.1,for

there existsε0>0 so small that for any givenε∈[0,ε0]andu0(x)satisfying(1.25),the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)admits a uniqueC1solutionu=u(t,x)on the domainD(T∗),and

whereC∗is a positive constant.

In what follows,we use a bootstrap argument to prove(3.8)–(3.9),namely,under the assumptions(3.8)–(3.9),we will prove that there existsT0>0 independent ofT,such that

By(3.3)–(3.4),we can takeγ>0 so small that

Noting(3.1),by the local well-poseness of theC1solution to the mixed initial-boundary value problem(1.1)and(1.15)–(1.17)(see[10]),there existsT0>0,such that the mixed initialboundary value problem(1.1)and(1.15)–(1.17)admits a uniqueC1solutionu=u(t,x)on the domainD(T+T0),and we have

To prove(3.11),we rewrite(2.17)as

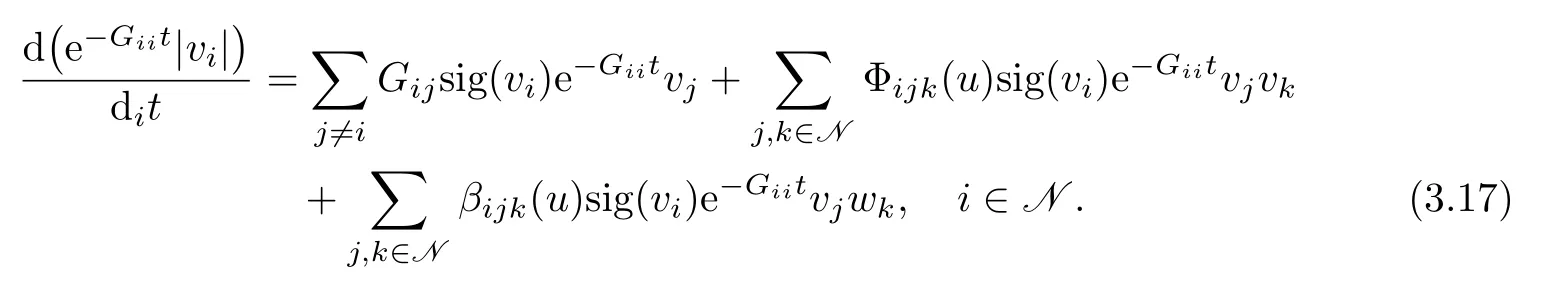
For eachs=m+1,···,nand any given point(t,x)∈D(T+)D(T),draw thesth characteristic curvepassing through(t,x):

which intersectsx=0 at the point(t0,0)(it can always be realized whenT>0 is large enough).Integrating(3.17)along the characteristic curvewith respect toτfromtot,we get

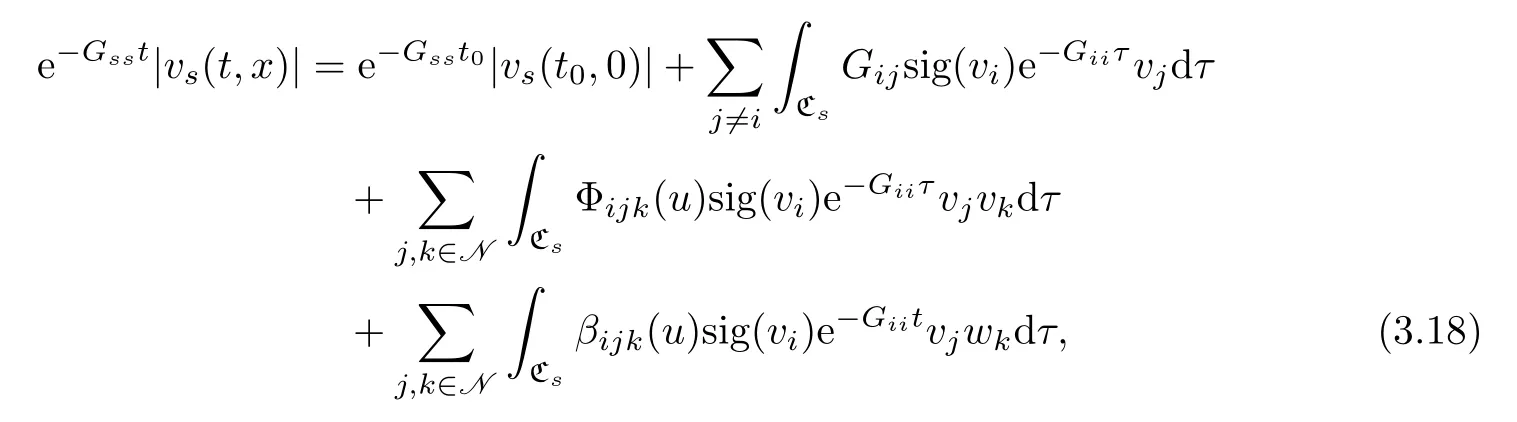
and then

where

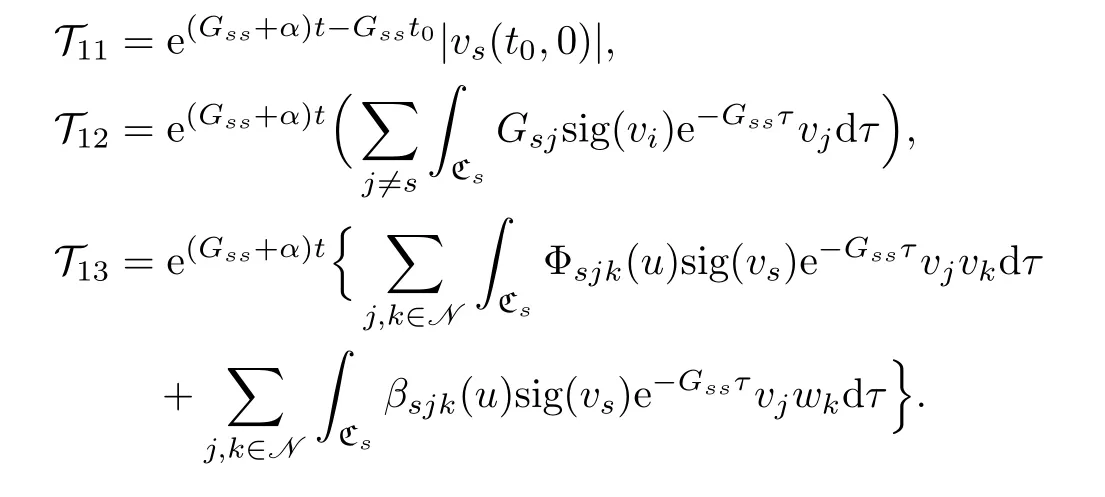
Using the boundary condition(2.21),we have

Noting(3.5)and(3.15)–(3.16),we get

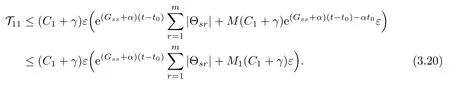
Similarly,we have

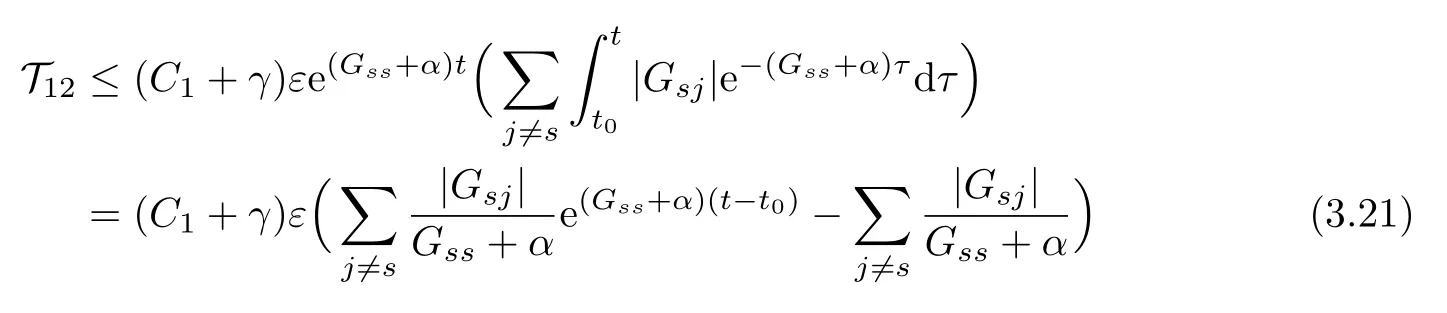
and

whereM1is a positive constant satisfying

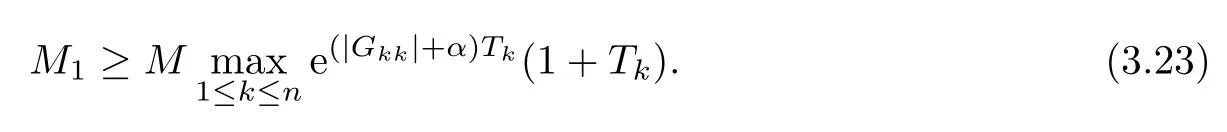
Substituting(3.20)–(3.22)into(3.19)and noting(3.3),we get

Noting(3.13)and thatε0>0 is small enough,we have

so

Forr=1,···,m,similar estimates hold.Thus,we get(3.11).

To prove(3.12),we rewrite(2.18)as

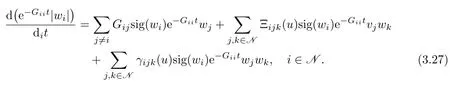
For eachs=m+1,···,nand any given(t,x)∈D(T+T0)D(T),draw thesth characteristic curvepassing through the point(t,x),which intersectsx=0 at the point(,0).Integrating(3.27)along the characteristic curveith respect toτfromtot,we get

where

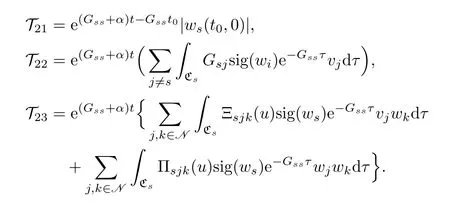
By the boundary condition(2.27),we have

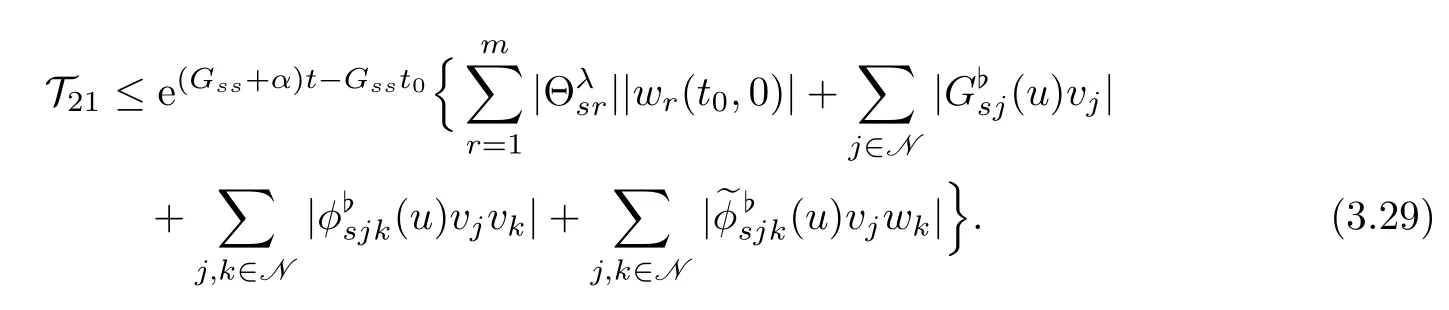
Noting(3.5),(3.11)andt−t0≤Ts,by(3.15)–(3.16),we have

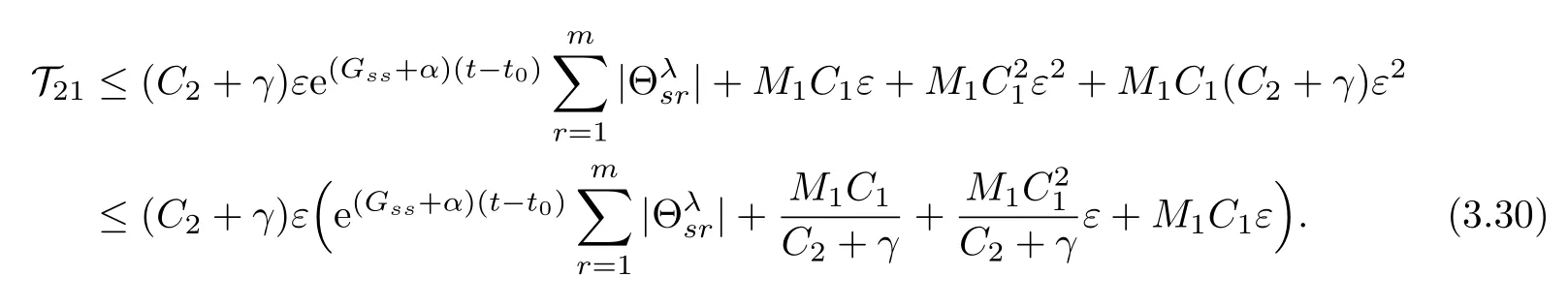
Similarly,we have

and

whereM1is given by(3.23).Substituting(3.30)–(3.32)into(3.28)and noting(3.4),we get

Noting(3.4)and 0<≪1,we can take≫M,such that

and then

Forr=1,···,m,similar estimates hold.Hence,we get(3.12)and complete the proof of Theorem 1.1.

Remark 3.1When=0,for the termin(3.19),the estimate(3.21)forshould be replaced by

while the estimates(3.20)and(3.22)forandstill hold.Noting(1.31),thesth term at the right-hand side of(3.3)should be replaced by

Similar treatments can be done forHence,Theorem 1.1 still holds,provided that(1.31)–(1.32)hold.

Remark 3.2If there exist Λ =and ∆ =such that

satisfy(1.26),and

satisfy(1.27),we can replace the variablesvandwin the proof of Theorem 1.1 by

respectively,and get the conclusion of Theorem 1.1.

Remark 3.3Suppose that the boundary conditions are given by

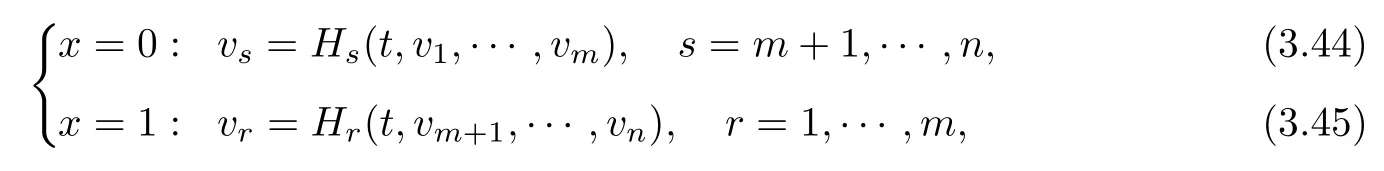
whereHrand(r=1,···,m,s=m+1,···,n)arefunctions of(t,···,and(t,v1,···,respectively,and

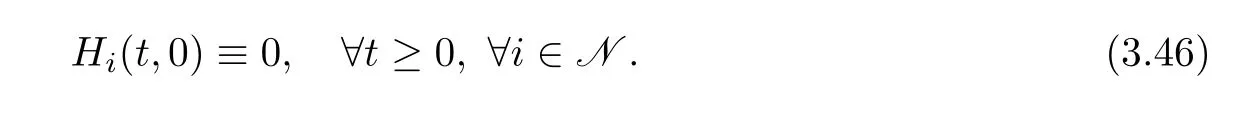
Let

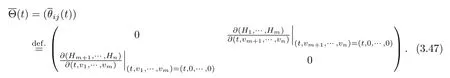
Then,boundary conditions(1.16)–(1.17)can be rewritten as

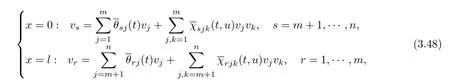
where(i,j,k∈N).Similarly,we have

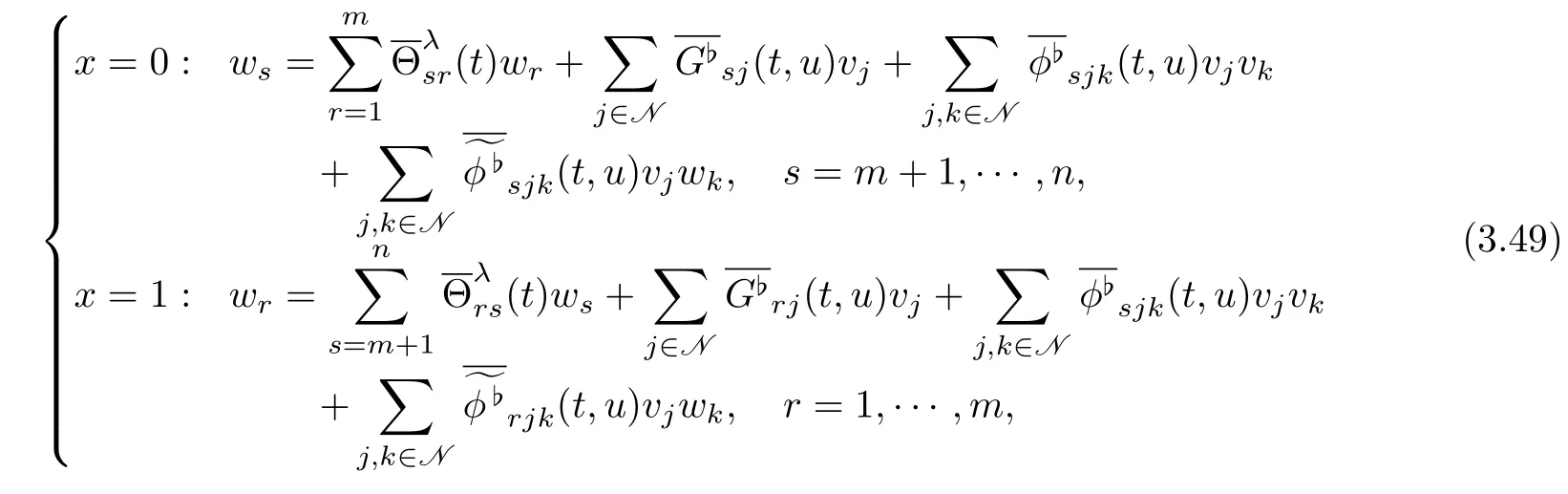
where(i,j,k∈N)are bounded continuous functions.

Comparing(3.48)–(3.49)with(2.21)and(2.27),through the procedure of the proof of Theorem 1.1,we can get the following theorem.

Theorem 3.1Under hypotheses(1.2),(1.10)and(3.46),if(1.26)–(1.27)hold,then there exists>0so small that for any given ε∈[0,],and any given initial data(x)satisfying(1.25)and(t,v)(i=1,···,n)satisfying≤ε(i,j=1,···,n,t>0),the conclusion of Theorem1.1is still valid.

4 Application

In this section,we give a kind of models to illustrate the application of Theorem 1.1.We consider the following mixed initial-boundary value problem for a system composed of two equations:

whereλ(Z,W)is aC2function of(Z,W),satisfying

κ>0,andα,βare constants.By Theorem 1.1,we have the following theorem.

Theorem 4.1Suppose that(4.6)holds.If|α|<1and|β|<1,then there exists >0so small that for any given θ∈[0,θ0]and any given initial data((x),(x))satisfying

the mixed initial-boundary value problem(4.1)–(4.5)admits a unique global C1solution(Z,W)=(Z(t,x),W(t,x))on the domain{(t,x)|t≥0,0≤x≤1},and there exists α>0,such that we have the following uniform a priori estimate:

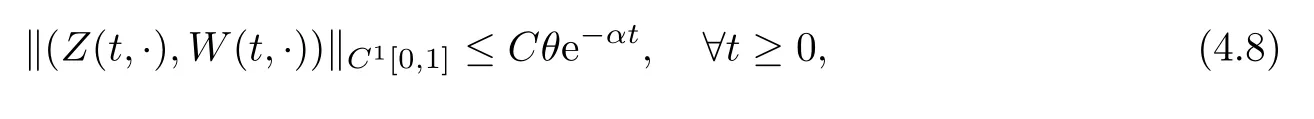
where C is a positive constant independent of θ and t.

Remark 4.1Some physical models can be written in the form of(4.1)–(4.2),for instance,thep-system with damping

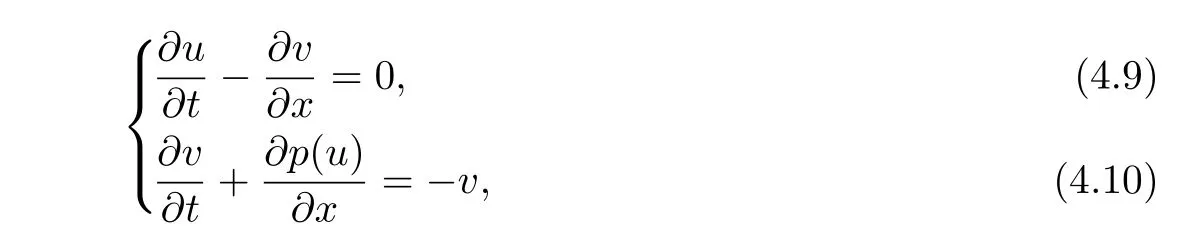
whereuandvstand for the specific volume and the velocity of the fluid.For polytropic gases,the pressurepis given by the following thermodynamic state equation(see[7]):

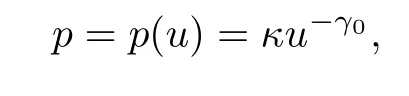
whereκ>0 and>1 are constants.

For any given>0,(,0)is an equilibrium state of system(4.9)–(4.10).Using the Riemann invariants

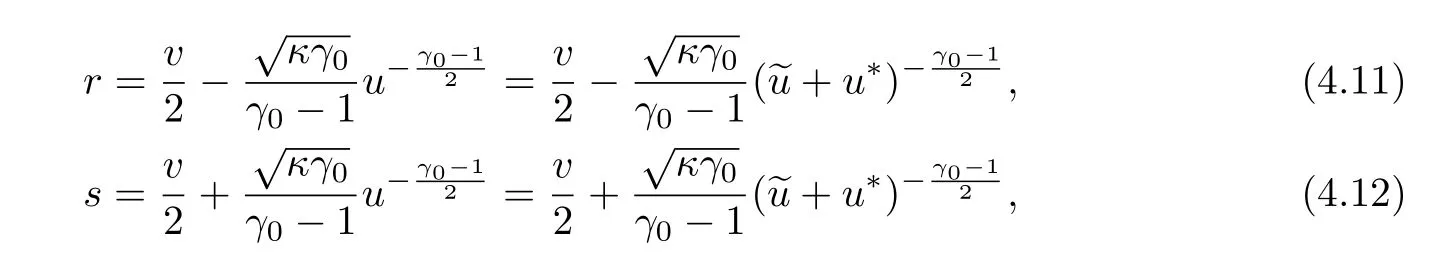
(4.9)–(4.10)can be rewritten as

where

(see[7]).

Moreover,for 1D linear wave equation

by the following transformation of variables:

we get

5 A Counterexample

In this section,we give an example to show that the conclusion of Theorem 1.1 may fail if(1.26)–(1.27)do not hold.

Example 5.1

The coefficient matrixA(u)of(5.1)–(5.2)is

whose eigenvalues are

Then

The inhomogeneous termF(u)is

and then

Moreover,the coefficient matrix Θ of boundary conditions(5.3)–(5.4)is

Thus,

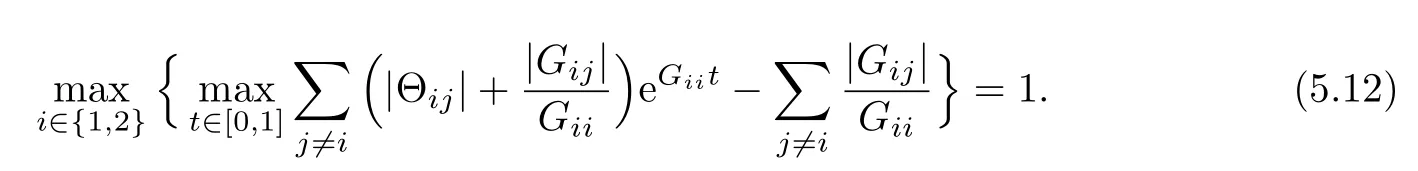
It is easy to see that the hypothesis(1.26)in Theorem 1.1 does not hold.

Let theC1[0,1]initial data(x)(i=1,2)satisfy

whereε>0 is a small parameter.By the conclusion in[9],the mixed initial-boundary value problem(5.1)–(5.5)admits a globalC1solution.In particular,we have

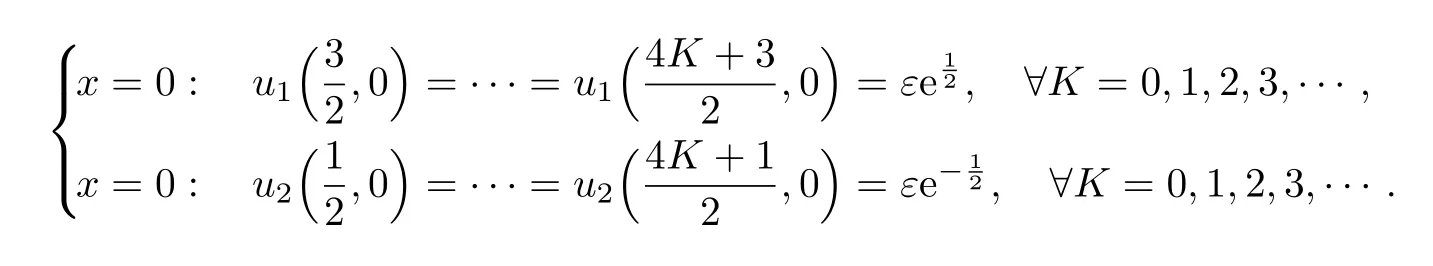
Hence,theC1solution to the mixed initial-boundary value problem(5.1)–(5.5)does not decay with respect tot.

6 Further Discussion on Theorem 1.1

First of all,the hypotheses(1.26)–(1.27)in Theorem 1.1 can be rewritten as

and

Case 1IfGii=0(i∈N),note that(1.29)–(1.30),(6.1)–(6.2)should be replaced by

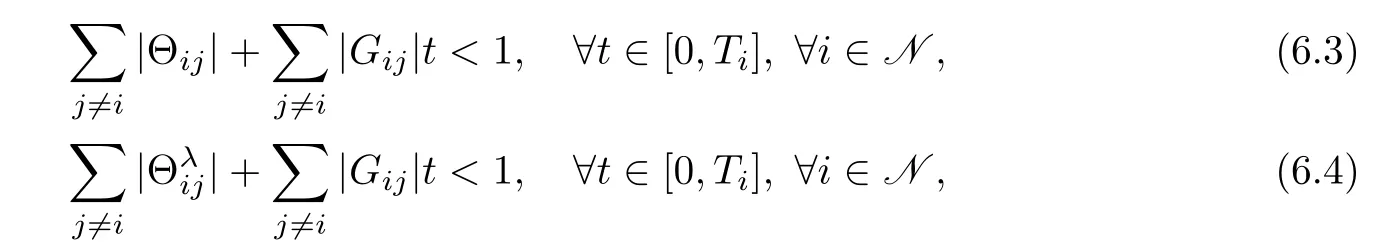
respectively.Specially,if=0(i,j∈N),(6.3)–(6.4)can be simplified to

respectively,which are the boundary dissipative condition for the quasilinear hyperbolic system without internal dissipative terms(see[6–7]).

Case 2If>0,then

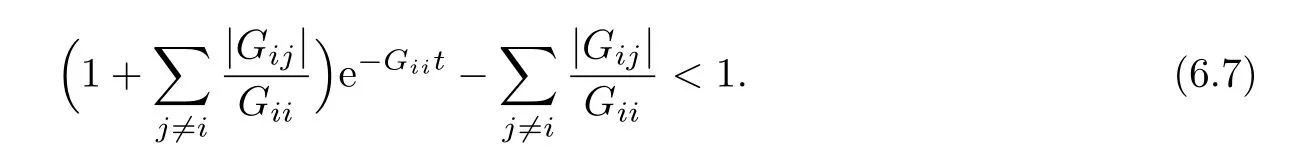
In this case,(6.1)–(6.2)indicate that if the inhomogeneous termF(u)has a growth effect forvi,a stronger boundary dissipative condition is needed to guarantee the exponential decay.

Case 3If<0,then

In this case,(6.1)–(6.2)indicate that if the inhomogeneous termF(u)has a reduced effect forvi,by a combination effect of the weaker boundary dissipative condition and the internal dissipative condition,theC1solution still decays exponentially.

[1]Beauchard,K.and Zuazua,E.,Large time asymptotics for partially dissipative hyperbolic systems,Arch.Rat.Mech.Anal.,199,2011,177–227.

[2]Bianchini,S.,Hanouzet,B.and Natalini,R.,Asymptotic behavior of smooth solutions for partially dissipative hyperbolic systems with a convex entropy,Commun.Pure Appl.Math.,60,2007,1559–1622.

[3]Coron,J.and Bastin,G.,Dissipative boundary conditions for one-dimensional nonlinear hyperbolic systems,SIAM J.Control Optim.,47(3),2008,1460–1498.

[4]Diagnea,A.,Bastin,G.and Coron,J.,Lyapunov exponential stability of 1-D linear hyperbolic systems of balance laws,Automatica,48(1),2012,109–114.

[5]Hanouzet,B.and Natalini,R.,Global existence of smooth solutions for partially dissipative hyperbolic systems with a convex entropy,Arch.Rat.Mech.Anal.,169,2003,89–117.

[6]Hsiao,L.and Li,T.T.,Global smooth solution of Cauchy problems for a class of quasilinear hyperbolic systems,Chin.Ann.Math.,4B(1),1983,109–115.

[7]Li,T.T.,Global Classical Solutions for Quasilinear Hyperbolic Systems,Research in Applied Mathematics,Masson John Wiley,Paris,1994.

[8]Li,T.T.,and Jin,Y.,Semi-global solution to the mixed initial-boundary value problem for quasilinear hyperbolic systems,Chin.Ann.Math.,22B(3),2001,325–336.

[9]Li,T.T.and Peng,Y.J.,The mixed initial-boundary value problem for reducible quasilinear hyperbolic systems with linearly degenerate characteristics,Nonlinear Analysis-Theory,Methods Applications,52,2003,573–583.

[10]Li,T.T.and Yu,W.C.,Boundary Value Problems for Quasilinear Hyperbolic Systems,Duke University Mathematics Series V,Duke University,Durham,1985.

[11]Liu,C.and Qu,P.,Global classical solution to partially dissipative quasilinear hyperbolic systems,J.Math.Pure Appl.,97,2012,262–281.

[12]Mascia,C.and Natalini,R.,On relaxation hyperbolic systems violating the Shizuta-Kawashima condition,Arch.Rat.Mech.Anal.,195,2010,729–762.

[13]Qu,P.,Global classical solutions to partially dissipative quasilinear hyperbolic systems with weaker restrictions on wave interactions,Math.Meth.Appl.Sci,36,2012,1520–1532.

[14]Qu,P.and Liu,C.,Global classical solutions to partially dissipative quasilinear hyperbolic systems with one weakly linearly degenerate characteristic,Chin.Ann.Math.,33B(3),2012,333–350.

[15]Yong,W.,Entropy and global existence for hyperbolic balance laws,Arch.Rat.Mech.Anal.,172,2004,247–266.

[16]Zhou,Y.,Global classical solutions to partially dissipative quasilinear hyperbolic systems,Chin.Ann.Math.,32B(5),2011,771–780.