条件风险下的两基金分离定理
向 华,杨招军,周伟峰
(1.青岛农业大学 合作社学院 山东 青岛 266109;2.湖南大学 金融与统计学院 湖南 长沙 410079; 3.青岛科技大学 数理学院 山东 青岛 266071)
条件风险下的两基金分离定理
向 华1,杨招军2,周伟峰3
(1.青岛农业大学 合作社学院 山东 青岛 266109;2.湖南大学 金融与统计学院 湖南 长沙 410079; 3.青岛科技大学 数理学院 山东 青岛 266071)
鉴于条件风险价值CVaR具有风险度量的合理性以及两基金分离定理对证券投资的重要意义,以CVaR作为风险度量研究两基金分离定理.在组合收益率服从正态分布的假设下,分别就投资组合含有或没有无风险资产的情形提出并证明了两基金分离定理;放开方差-协方差矩阵为非奇异这一通常假设,证明了CVaR风险度量下的两基金分离定理依然成立.
条件风险价值;正态分布;两基金分离定理;奇异
1 引 言
随着金融市场风险的加大,金融机构正面临着日趋严重的风险,作为高风险的行业的证券业,如何给出其投资组合的风险度量是防范和控制风险的先决条件.自Markowitiz.H[1]于1952年给出了以资产收益率的方差作为风险度量以来,由于方差作为风险度量的缺陷,不断有学者提出新的风险度量方法.最具代表性的是1999年Rockafellar and Uryaser[2]首次提出的CVaR风险度量方法, 由于该风险度量同时满足正齐次性、次可加性、单调性和传递不变形, 不仅弥补了方差和VaR度量的一系列缺陷而且是一致性的风险度量方法,吸引了中外学者的极大关注.例如,Palmquist[3]给出了均值-CVaR有效前沿的三种等价描述,并对CVaR的概念,性质,计算及优化等做了详细的介绍.Rockafellar and Uryasev[4]还对损失服从一般分布的CVaR模型进行了研究.在国内,刘小茂和李楚霖[5]讨论了正态情形下风险资产组合的均值-CVaR的有效前沿,并与均值-方差模型进行了比较.林旭东和巩前锦[6]给出了均值-CVaR模型的有效前沿的表述,总结并推导了有效前沿的性质.但他们都没有对该风险度量下的两基金分离定理是否成立进行推导和证明.
本文余下结构安排如下:第二节为条件发风险的定义;第三节证明了风险资产组合下的两基金分离定理;第四节证明了含有无风险资产下的两基金分离定理;第五节在资产存在相关性的条件下证明了两基金分离定理;最后一节是本文的结论.
2 CVaR的定义及一些结果的介绍
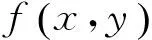
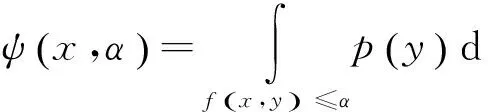
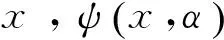
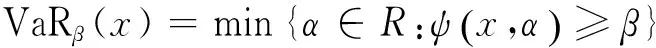
此外类似线性代数,下面引入随机变量的线性相关、线性无关与极大线性无关组的概念.设η1,η2,…,ηn为任意方差不为0的随机变量组.
定义1 若存在不全为0的实数k0,k1…kn,使得k1η1+k2η2+…+knηn=a,a为常数,则称η1,η2,…,ηn是线性相关的,否则是线性无关的[9-11].
定义2 若存在实数k0,k1…kn,使得η=k0+k1η+…+knηn, 则称η可以由η1,η2,…,ηn线性表出[9-11].
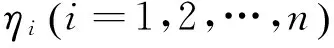
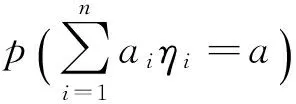
3 不含无风险资产的两基金分离定理
假定投资组合不含无风险资产,且风险资产的数目为n.若投资组合的收益率服从正态分布,投资者以CVaR为风险度量的组合优化问题为:
(1)
其组合边界方程为
(2)
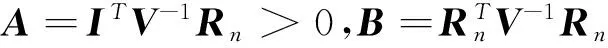
C=ITV-1I>0,D=BC-A2.
最优投资组合为W=λV-1Rn+rV-1I,
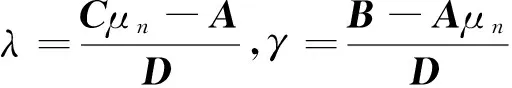
类似均值-方差模型下两基金分离定理,有:
定理1 在收益率服从正态分布的条件下,均值-CVaR边界上任何两个期望收益率不相等的组合Wa,Wb均可以生成整个组合边界,即是说对任何一个组合边界W,都存在实数α,β使得
W=αWa+βWb.
证明 本文先证明组合边界上任意一组合W可以由最小风险组合Wmvp和组合边界上另一组合Wd生成.为此先求出这两个投资组合.最小风险组合Wmvp可以通过式(2)关于均值的一阶偏导可得,即
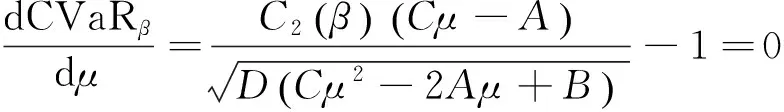
整理得均值的方程为
其判别式为
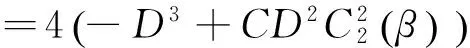
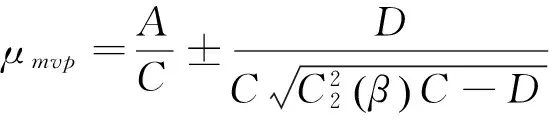
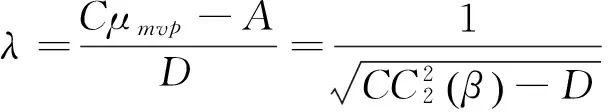
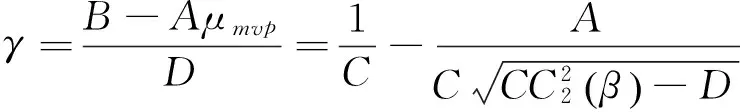
因此
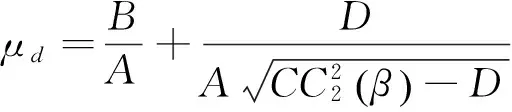
对边界上的任一组合W是否可以由Wmvp和Wd生成,即证是否存在常数α,β,且α+β=1,使得:
W=αWmvp+βWd.
假定有α∈(0.1)使得下面方程成立:
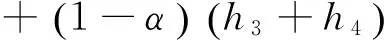
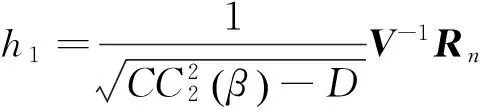
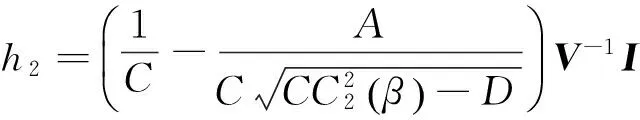
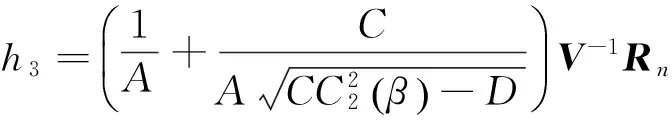
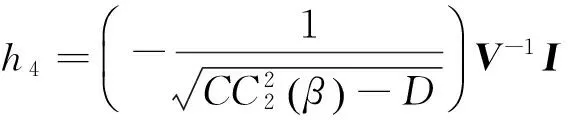
该问题等价于有没有相同的α使得以下两方程的同时成立,
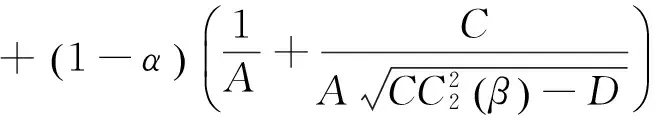
(3)
(4)
从式 (3)和 (4) 分别解得
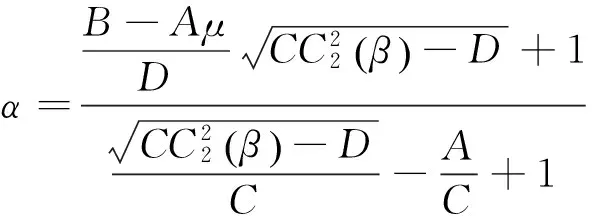
因此,只需证明:

4 含有无风险资产的两基金分离定理
当投资者在市场上可获得无风险资产时(其收益率为无风险利率rf),若设W=(W1,W2,…Wn)T为n个风险资产的投资比例向量,则投资在无风险资产上的比例为1-WTI.类似上节,组合优化问题为:
(5)
其组合边界方程为:
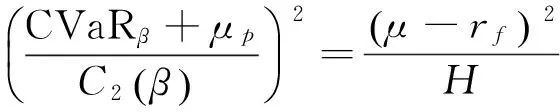
其中
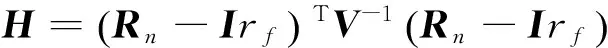
对应的最优解为
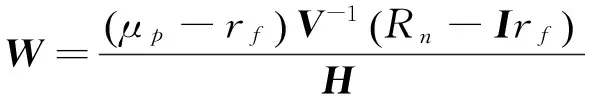
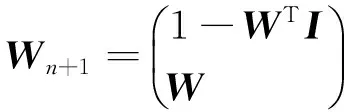
定理2 在资产收益率服从正态分布的假设下,含有无风险资产的均值-CVaR边界上任何2个期望收益率不相等的组合Wa,Wb均可以生成整个组合边界,即是说对任何一个组合边界W,都存在实数α,β使得:
W=αWa+βWb.
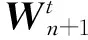
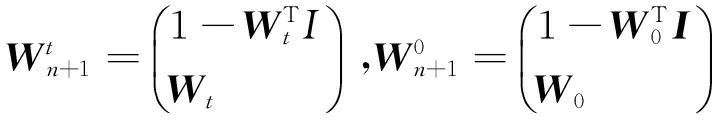
类似于均值-方差模型,来看组合边界上的任一合Wn+1是否可以由切点组合和风险为零的组合生成,即:是否存在这样的实数α,β且α+β=1使得:
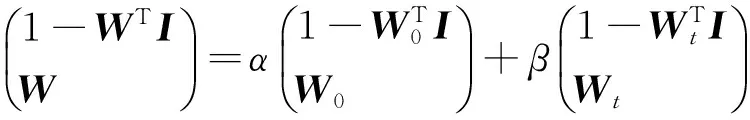
等价于是否存在实数α使得以下两式同时成立:
(6)
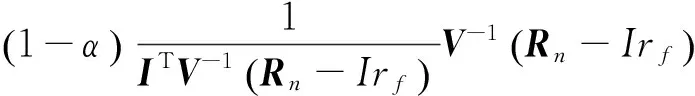
(7)
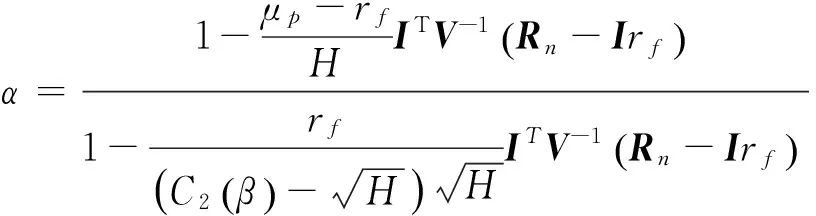
W=αWa+βWb,证毕.
4 协方差矩阵为奇异的两基金分离定理

(8)
其中
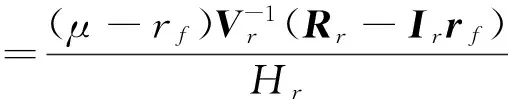
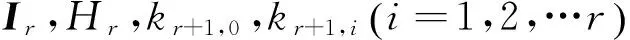

则最优解可以简化为:
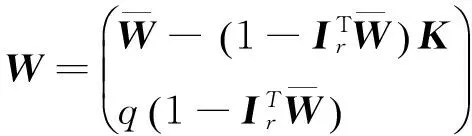
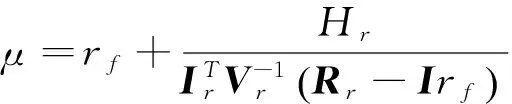
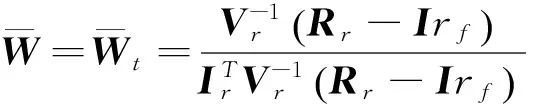
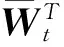
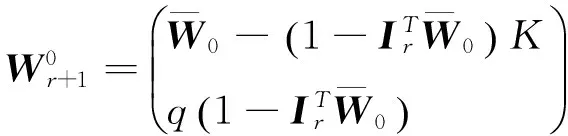
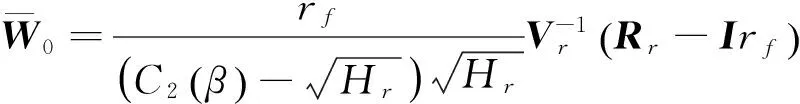
定理3当方差-协方差矩阵V奇异时,对于情形1两基金分离定理成立,对于情形2,风险资产的极大无关组和无风险资产可生成原n个风险资产的组合边界,两基金分离定理仍然成立.
5 结 论
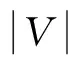
[1]HMARKOWITZ.Portfolioselection[J].TheJournalofFinance, 1952, 7(1): 77-91.
[2]TROCKAFELLER,SURYASEV.Optimizationofconditionalvalue-at-risk[J].JournalofRisk, 2000, 2(1):21-42.
[3]JPAMQUIST,SURASEV,PKROKHMAL.PortfoliooptimizationwithconditionalValue-at-Riskobjectiveandconstrains[J].JournalofRisk, 2002, 4(2):319-332.
[4]TROCKAFELLER,SURYASEV.Conditionalvalue-at-riskforgenerallossdistributions[J].JournalofBankingandFinance, 2001, 26(7): 1443-1471.
[5] 刘小茂, 李楚霖, 王建华. 风险资产组合的均值-CVaR有效前沿 (1)[J]. 管理工程学报, 2003, 17(1): 29-33.
[6] 林旭东,巩前锦. 正态条件下均值-CVaR有效前沿的研究[J].管理科学,2004,17(3):52-55.
[7] 李杰,张红兵,费时龙,等.Mean-CVaR模型下的两基金分离定理[J]. 宿州学院学报2011,26(2):8-10.
[8] 曹静,秦超英.Mean-CVaR模型下的两基金分离定理[J].系统工程学报2006,21(2):201-205.
[9] 姚海祥. 均值方差模型下证券投资选择的进一步研究[D]. 广州: 华南师范大学数学科学学院,2005.
[10]向华,周伟峰. 协方差矩阵为奇异的均值-CVaR模型的研究[J]. 重庆工商大学学报: 自然科学版,2010, 27(4): 327-330.
[11]向华, 杨招军. 跳过程下的公司证券定价和最优资本结构[J]. 中国管理科学, 2014(8):29-36.
Two Fund Separation Theorem under The Condition at Risk
Xiang Hua1, YANG Zhao-jun2,ZHOU Wei-feng3
(1.School of cooperative, Qingdao Agricultural University, Shandong,Qingdao 266109,China;2. School of Finance and Statistics , Hunan University, Hunan,Changsha 410079,China;3. School of Mathematics and Physics, Qingdao University of Science and Technology, Shandong, Qingdao 266071,China)
Based on the rationality of the conditional value at risk as well as the important role of two fund separation theorem on securities investment, this paper analyzed the two fund separation theorem. For the portfolio with or without risk-free asset, we proved two fund separation theorem under the assumption that the portfolio return follows normal distribution. Further, we find that two fund separation theorem remains valid if the variance-covariance matrix is singular.
conditional value-at-risk; normal distribution; two fund separation theorem; singular
2015-10-03
国家自然科学基金(71221001,71371068),山东省自然科学基金(ZR2015PF001),中国博士后面上一等资助(2015M570594)
向 华(1974—),男 ,湖南洪江人,讲师,博士
E-mail:xianghua320@sina.com
F830
A

