一种横观各向同性沉积岩的失效准则★

任述光 刘保华 乔金丽

(1.湖南农业大学工学院，湖南 长沙 410128； 2.河北工业大学土木工程学院，天津 300130)

·岩土工程·地基基础·

一种横观各向同性沉积岩的失效准则★

任述光1刘保华1乔金丽2

(1.湖南农业大学工学院，湖南 长沙 410128； 2.河北工业大学土木工程学院，天津 300130)

通过定义初始屈服函数及由试验测定沉积岩的参数，提出了一般应力条件下岩石材料的失效准则，给出了该准则的数学表达式，对两种典型横观各向同性岩石强度特性的模拟结果表明，该准则能较好地反映沉积岩类材料在一般应力条件下的强度变化规律。

沉积岩，横观各向同性，失效准则，微结构张量

0 引言

也可以借助临界平面或弱方向存在性的概念表达材料的屈服和失效，沿此平面或方向失效函数取极大值。这种定义屈服函数方法的不便是需要定义大量的材料函数或参数，并且这些参数与材料微结构间的关系是相当含糊的。现有的一些反映各向异性的强度准则大多适用范围有限，并且缺乏明确的物理含义。Abelev等提出了绕主应力空间原点旋转的应力变换方法，但仅适用于应力主轴与材料主轴重合的情况。张卫明提出了一般应力条件下各向异性粒状材料的强度准则，该准则假定不同平面上的摩擦角随该平面与沉积面之间的夹角变化，称为ASMP准则，给出了该强度准则在横观各向同性条件下的表达式。平面应变条件下，陈越在Mohr-Coulomb强度准则基础上，从单元极限平衡的角度建立各向异性强度准则，但该准则不适用于一般的应力条件，因为无法反映中主应力的影响。

定义屈服和失效准则更严密的方法是利用应力和微结构张量混合不变量的表达理论，它首先出现在Boehler的论文中，随后Nova加以扩展。屈服函数的一般形式为F(σ)=F(σij)=0，可以用应力张量分量的二次多项式表示，它是各向异性的标量值函数，即F(σ)≠F(QgσgQT),Q为正交张量。当用主应力表示初始各向同性的岩土类材料，其屈服函数的形式不依赖于所选择的坐标系，与三个主应力相对于材料坐标轴的方向无关，只与三个主应力大小有关。这时屈服函数可用应力张量和偏张量的三个不变量表示为F(I,J2,J3)=0。研究各向异性张量函数和各向异性材料本构方程的集大成者是Boehler，在他的论文中，利用空间各向同性原理将表征材料各向异性的张量或结构张量的概念成功扩展，一些各向异性张量函数的表示由各向同性张量函数的结果导出。这一理论能较好解释横观各向同性，正交异性和斜交异性材料的复杂不可逆力学现象，如屈服、失效、蠕变和损伤。

1 各向异性参数的定义

表征材料性质的一切方程或函数都应具有和材料性质相同的对称性，称为连续介质力学的Newman原理。根据这一原理的结论，横观各向同性材料的屈服函数可以表示为五个标量不变量的函数:

F(σ,a)=F(trσ,trσ2,trσ3,traσ,traσ2)=0

(1)

其中,trσ,trσ2,trσ3分别为应力张量的一阶、二阶、三阶矩。式(1)是σ,a的各向同性张量函数，即对于任意正交张量Q:

F=F(σ,a)=F(QgσgQT,QgagQT)=0

(2)

以上方程中a是实对称二阶张量，它是材料内部结构的度量，表征材料微观结构，例如，孔隙和微裂纹的空间分布，材料颗粒间排列接触情况等。由各向同性张量函数的表示定理，它可写为:

F=F(σ,a)=F(trσ,trσ2,trσ3,η,β)=0

(3)

η表示张量在某一定义的加载方向l的投影的各向异性标量，定义为:

在本体系结构下，每个电站的状态监测系统自成体系，可独立运行，便于系统调试和现场工程师应用。无论在电站还是办公大楼区域，通过应用服务器与管理信息系统（Management Information System，MIS）或计算机局域网相连，可以充分利用MIS网上的每一台计算机进行状态监测分析和诊断。

(4)

微结构张量a的三个主方向与正交异性材料主轴共轴。荷载相对于材料主轴的方向效应便可由各向异性参数η定义。η就是应力张量和微结构张量乘积的联合不变量与应力二阶矩的比值。式(4)的另一种表达方法是利用微结构张量a的无量纲化了的偏张量A，使得:

(5)

trA=A1+A2+A3=0

(6)

通过引入高阶张量A的并积，例如Aijkl=b1AijAkl;Aijklmn=b2AijAklAmn等，式(5)中η可以写为如下更一般的表示形式:

(7)

式(7)又可写为:

(8)

2 初始屈服函数

通过将经典的各向同性屈服准则在塑性理论框架加以推广，提出了一个各向异性屈服准则，假设可以用应力和偏应力张量的不变量表示失效准则，这一准则适合于岩石类脆—塑性材料。它可以由式(9)给出的等效应力的二次式表示为:

(9)

(10)

因此出现在失效准则一般式(3)中的各向异性参数η与这里的fc是等同的。因为fc值依赖于应力张量和微结构张量的相对方向。一般情况下，材料的单向拉伸和双向压缩强度都与fc成正比，因此fc是唯一独立的强度参数。式(9)是主应力空间中一个不规则的锥体，其与p-q子午面的交线为一光滑曲线，在π平面的投影是一个非圆的外凸曲线，曲线的形状取决于函数g(θ)。

进一步分析可知式(9)可以写为以下简化的等效式:

(11)

3 屈服函数中参数的确定

在应用屈服准则式(9)时，需要确定其所涉及的材料参数及材料函数，特别是与式(10)对应的分布函数相联系的参数，它描述单轴压缩强度的变化。图1是试验给出的页岩单轴压缩强度随层理面方位与压缩轴交角α变化的相关试验数据。显然，α=0，即加载方向与层理正交时强度最高。

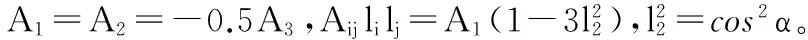
因此：

(12)

根据不同加载方向得到的强度值对实验数据进行拟合，可以确定系数:

(13)

利用不同初始围压下的三轴实验的结果，可以确定出现在屈服准则式(11)中的材料常数。

表1应力条件数据是α=0时测得的最终强度。

表1 应力强度三轴试验结果

表1中σx=σz确定了围压的大小(加载过程中围压保持不变)，σy是轴向压力的最大值。这里加载路径相应于式(9)中,θ=π/6,g(θ)=1。

因此:

(14)

(15)

将式(14)的二次多项式函数曲线拟合，得到拟合系数结果为：

c1=2.372 9;c2=0.937 1;c3=0.658 2。

将拟合系数和页岩的单轴压缩强度数据代入屈服准则式(13)化简后可得：

(16)

为检验这一模型的正确性，进行了一系列的三轴试验模拟，实验材料为页岩，在不同初始围压下进行三轴试验，沿试样不同方向进行加载，数值结果如图2所示，分别为围压在5MPa，30MPa，40MPa时垂直于试样加载时偏应力张量对轴向应变图。

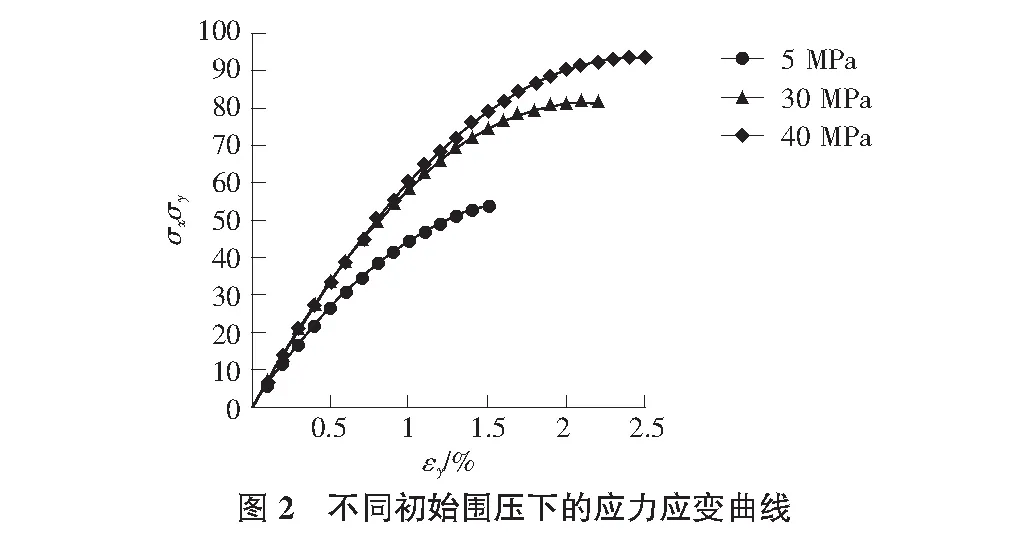
4 结语

1)通过引入了反映材料微结构张量在指定加载方向的投影的标量参数η，本文给出了一种描述具有横观各向同性性质的岩石类材料的屈服失效数学模型。

2)在这一模型中，岩石材料的内在横观各向同性被描述为标量参数η围绕其平均值的变动。

3)试验表明，理论与试验结果符合较好，式(9)可作为横观各向同性岩石的屈服准则。

4)这一准则使用基本应力不变量与应力张量二阶混合不变量和结构方向张量，可以减少复杂的数学运算。

A failure criterion for transverse isotropy sedimentary rocks★

Ren Shuguang1Liu Baohua1Qiao Jinli2

(1.CollegeofEngineering,HunanAgricuturalUniversity,Changsha410128,China;2.SchoolofCivilEngineering,HebeiIndustrialUniversity,Tianjin300130,China)

Through the initial determination of yield function and right test defining sedimentary rocks parameters, this paper put forward the failure criterion of rock material under general stress condition, given the mathematical expressions of the criterion, the simulation results showed that of two kinds of typical transversely isotropic rock strength characteristics, this criterion could well reflect the strength variation laws of sedimentary rock material in general stress condition.

sedimentary rock, transversely isotropic, failure criterion, micro structure tensor

2014-11-21 ★：湖南农业大学人才基金项目(项目编号：08YJ02)

任述光(1970- )，男，博士，副教授； 刘保华(1973- )，女，副教授； 乔金丽(1978- )，女，副教授

1009-6825(2015)04-0054-03

TU431

A