基于二维粒子群优化的图像模糊增强算法研究

白 冰，马 瑜，杨晓丽，孟亚州，魏晶茹

(1.宁夏大学 研究生院，宁夏 银川 750021； 2.宁夏沙漠信息智能感知重点实验室，宁夏 银川 750021)

基于二维粒子群优化的图像模糊增强算法研究

白 冰1，马 瑜1，杨晓丽2，孟亚州1，魏晶茹1

(1.宁夏大学 研究生院，宁夏 银川 750021； 2.宁夏沙漠信息智能感知重点实验室，宁夏 银川 750021)

针对传统基于灰度变换方法进行图像增强后图像质量不高等现象，对粒子群优化算法、模糊增强算法进行研究，同时结合禁忌搜素和粒子空间对称分布原理，提出一种基于二维粒子群优化的图像模糊增强算法。该算法通过对搜索粒子进行空间对称分布调整以避免算法陷入局部最优、提高全局搜索能力，并且在算法迭代后期加入禁忌搜索算法记录粒子搜索位置，以减少粒子位置重复寻优、提高算法搜索效率。最后将改进后的粒子群优化算法中粒子搜索位置和速度更新方向设定为二维并与模糊增强算法相结合，自适应搜索出模糊参数Fp和Fe最优值，实现模糊增强。实验结果表明，改进后算法对图像增强效果较好，并且将算法用于过暗SAR图像、医学MR图像的增强，可有效提高图像质量。

二维粒子群优化；粒子空间对称分布；禁忌搜索；模糊增强；自适应寻优

图像增强作为图像初级处理阶段中的一项重要的技术，可通过提高图像清晰度、扩大图像中不同物体特征之间的差别以提高图像的分辨率、对比度并为后续的图像分割、边缘提取以及模式识别等深层次处理提供了技术基础[1-2]。一般的灰度图像增强技术根据图像所在的空间不同，分为基于空域增强和基于频域增强两类[3]。

基于空域增强的图像增强方法通常分为5种：灰度变换增强、直方图增强、图像平滑、图像锐化和基于数学理论的增强。其中，图像的灰度变换增强是最先引用且广泛使用的增强方法。主要通过改变原始图像数据所占的灰度范围而使图像在视觉效果上得到改观。随着研究的不断进展，在传统灰度变换增强算法中常引入数学原理，提出多种基于数学理论的灰度图像增强方法，根据算法模型、方程参数值的不同对图像进行增强操作。其中，邸慧等人利用分段线性灰度增强技术，使目标区域得到增强[4]，但是该方法需人为参与调节方程中3个参数值以调整曲线的位置和形状来达到增强目的，误差较大。龚昌来等人提出一种改进正弦灰度变换的图像增强算法，根据图像的灰度分布进行自适应选择[5]，但是图像灰度值较大区域增强效果不够明显。李均利等人基于模糊数学方法提出一种结合小波变换原理的图像增强方法，对图像有一定的增强效果[6]，但是算法复杂度较高。陈延梅等人采用一种模糊逻辑将二值形态学分级算子推广到灰度图像[7]，但是该方法理论原理复杂、算法效率较低。

因此，针对以往基于数学理论的灰度图像增强方法中所普遍出现的增强效果不理想、需要人为干预和算法精度低等问题，本文根据图像采集后本身存在被模糊化的特性，基于粒子群优化算法结合禁忌搜索算法和粒子空间分布原理，提出一种基于二维粒子群优化的图像模糊增强算法，自适应的搜索出模糊清晰度函数中两个参数值，使图像在模糊域与空域相互变换的过程中有最大模糊清晰度。

1 改进粒子群优化算法

1.1 传统粒子群优化算法

粒子群优化算法是由美国的学者Eberhart和Kennedy在1995年提出的仿生类算法[8]，源于对鸟群和鱼群群体运动行为的研究。随着研究的不断进展，粒子群优化算法已在组合优化和函数优化中有了广泛的应用，为了一种优化效率较高的优化工具[9-10]。在寻优过程中，粒子的速度和位置随着搜索的进程在不断更新，使得算法具有很好的导向性，但是这种导向性同时会导致算法陷入局部最优解，收敛过早。

如图1所示，在一定搜索范围内由于所有粒子都分布在局部最优解以及全局最优解一侧，而且最早接触局部最优解，因此会有算法过早收敛且粒子陷入局部最优解的情况出现。

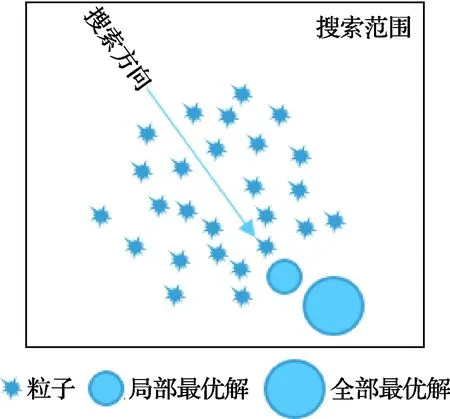
图1 搜索陷入局部最优解

1.2 二维粒子群优化算法的改进

根据传统粒子群优化算法在寻优过程中所出现的容易陷入局部最优解的问题，利用空间对称分布原理，自动调整若干粒子的位置分布，使粒子的位置尽量在局部最优解的周围而不是一侧，并且保证在当前全局最优解两侧的粒子个数均衡，以减少粒子陷入局部最优解的情况发生。

同时，考虑到若将粒子对称分布调整后的粒子群优化算法与模糊算法进行融合，会增加混合算法的收敛时间影响粒子群算法的寻优速度，因此加入具有较强“爬山”能力的禁忌搜索算法[11-12]，并借助禁忌表的存档优势自动判断某一位置是否已经被搜索过，可以避免重复搜索、提高算法效率。

与模糊算法的结合，需要寻找两个未知参数，因此将粒子搜索位置和速度更新方向设定为二维。

改进二维粒子群优化算法寻优过程概述如下：

1) 随机初始化每个粒子，并且禁忌表初始化。

设置空白禁忌表table1,table2,table3,table4。设种群共有N个粒子，搜索空间为D维空间，若搜索两个未知量数值，则第i个粒子的位置向量可表示为

(1)

其飞行速度向量可表示为

(2)

每个粒子所各自维护的自身历史最优位置向量可表示为

(3)

群体所维护的全局最优位置向量可表示为

(4)

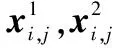
2) 判断此处结束条件是否满足。若满足则转至步骤8)，若不满足则继续步骤3)。

3) 更新每个粒子的速度和位置。每迭代一次，速度和位置更新一次。

飞行速度向量更新方程为

(5)

位置向量更新方程为

(6)

式中：gap代表迭代次数；w为惯性权重系数；c1，c2为学习系数；rand1、rand2为介于[0，1]间的随机数且相互独立。

(7)

(8)

(9)

式中：T是当前迭代次数；Tmax是最大迭代次数；wmax和wmin为w的最大值和最小值；cmax和cmin为c1和c2的最大值和最小值。

4) 计算每个粒子的适应度值，确定候选位置(解)。

设置：目标函数为

(10)

约束条件为

(11)

评价函数为

(12)

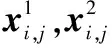
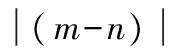
(13)

(14)

式中：gbestk为在j=k维处群体所维护的全局最优位置，rand为介于[0，1]间的随机数。

6)判断粒子是否重复搜索某一位置。

7)粒子选择该处已搜索位置附近所未搜索位置进行搜索，转至步骤2)。

8)输出群体所搜索到的全局最优解，程序结束。

2 改进二维粒子群优化的模糊增强算法

2.1 传统模糊增强算法

图像在采集过程中由三维景象向二维进行映射时，不可避免地存在图像信息丢失，所以图像具有模糊性。针对这一特点，Pal.S.K等人提出了一种模糊增强算法[13]，将模糊数学理论引入到图像增强中。

图像的模糊增强算法是在图像所建立的模糊特征平面上对图像的像素进行处理。算法中所含有的两个模糊参数Fp和Fe的取值直接影响模糊特征平面P的模糊性的大小，因此合理选择参数Fp和Fe是保证增强效果的重要环节。目前Fp和Fe的选取多凭程序使用者经验或观察图像灰度分布等方法确定，一般需要经过多次的尝试。对于比较复杂的图像，理想的Fp和Fe很难找到。

算法操作流程主要分为3步执行：对原始图像利用模糊特征函数式(15)进行模糊特征提取、利用模糊增强算子式(16)进行增强变换、利用式(15)的逆变换进行特征还原。

(15)

(16)

目前模糊算法在图像的增强应用中，较为经典的有叶志伟等人所提出一种基于PSO的图像自适应模糊增强算法[14]。但是在算法中令参数Fe=1仅自动寻优参数Fp的值，并且未考虑粒子群优算法自身所存在的易陷入局部最优的问题，使得混合算法精度依然有待于提高。

2.2 二维粒子群优化与模糊增强算法结合

本文将模糊算法与改进的粒子群优化算法相结合，自动寻找模糊参数Fp，Fe的最优值以确定增强后的图像有最大的模糊清晰度函数H(P)。与传统基于数学理论的灰度变换图像增强方法相比，充分考虑到了图像的复杂性以及图像处理过程中的模糊性；与传统基于粒子群优化的模糊增强方法相比，还可以自适应的搜索两个模糊参数值，有效的改善了原始图像的视觉效果。

本文所提出算法对图像增强过程概述如下：

1)随机初始化每个粒子，初始化禁忌表table1，table2，table3以及table4。

2)判断此处结束条件是否满足。若满足则转至步骤11)，若不满足则继续步骤3)。

3)更新每个粒子的速度和位置。

考虑到寻找模糊参数Fp和Fe的最优值，采用上文改进二维粒子群算法对第i个粒子速度更新和位置更新方程。

4)确定模糊参数，利用模糊特征函数式(15)进行图像模糊特征的提取，生成模糊特征平面。

5)计算每个粒子的适应度值，确定候选位置(解)，进行禁忌表的更新。

为了定量测定图像增强后的质量，在算法中采用模糊清晰度函数H(P)评价图像增强的质量[15]。将H(P)作为适应度函数，寻找最大值以确定模糊参数Fp、Fe的最优值。

H(P)= lg[(Sd(i)+0.1·Ffd(i)/

Fcs(i))·Gl(i)·E(i)]

(17)

式中：Sd(i)为模糊增强后图像的标准差(Standard deviation)；Ffd(i)为图像的模糊特征平面的模糊清晰度值(Fuzzy feature definition)；Fcs(i)为图像模糊特征平面的模糊紧支度值(Fuzzy compactly supported feature plane)；Gl(i)为模糊增强后图像的灰度级数(Gray levels)；E(i)为模糊增强后图像的信息熵(Entropy)。

此时，目标函数设定为

(18)

之后，将当前粒子位置、粒子历史最优位置向量分别放入禁忌表table1和禁忌表table3中；将当前粒子位置、群体所维护的全局最优位置向量分别放入禁忌表table2和禁忌表table4中。

6)基于粒子空间分布对称原理，根据式(8)对粒子进行位置调整。

7)判断粒子是否重复搜索某一位置。

通过禁忌表table1和table3中所存位置向量的对比判断，以确定下一次的搜索位置是否重复。若位置未被重复搜索，则继续8)；若位置被重复搜索，则转至2)执行操作。

8)通过判断，粒子此时需选择已搜素位置附近未搜素位置进行搜索，即算法直接转至3)。

9)图像模糊增强变换。在所得模糊特征平面上，利用模糊增强算子式(16)进行增强变换，获得新的模糊特征平面。

10)在新的模糊特征平面上利用式(15)的逆变换进行特征还原。

11)输出增强后图像，程序结束。

算法流程图如图2所示。

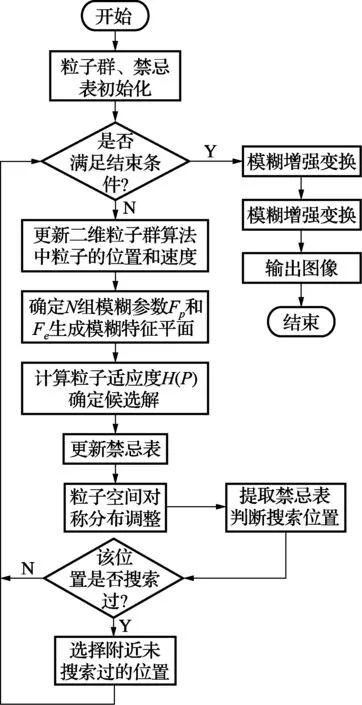
图2 基于二维粒子群优化的图像模糊增强算法流程图

3 实验结果和分析

为了验证本文所提出的基于二维粒子群优化的图像模糊增强算法的可行性及针对图像进行增强后与经典的传统灰度变换(CTGT)增强方法、传统基于粒子群优化的模糊(TFPSO)增强方法相比会有更好的增强效果，本文选用过暗常用lena图像、过暗SAR图像和过暗医学MR图像分别进行了处理。软件使用MATLAB R2009b版本，硬件环境为主频1.8 GHz、内存4 Gbyte的Windows8系统便携式笔记本电脑。算法中最大迭代次数为100次，粒子个数为100个，所用图像大小为 256×256。

3.1 图像增强结果对比

实验1：选取带有背景物的过暗常用Lena图像，如图3a所示。图3b为使用CTGT增强方法中的分段线性增强算法后所得结果，但是由于图像灰度变化具有一定的随机性，需要人工经验调整算法3个参数值，最后往往得不到满意的增强效果，图像的增强效果不理想。图3c、图3d分别为TFPSO增强方法和利用本文方法对图像增强后结果。可以看到与原始图像相比，两种方法增强后图像质量都有了较大的提高，而且利用本文增强方法增强后的图像效果比使用TFPSO增强方法后的图像效果在视觉上又有了进一步提高。

图3 对Lena图像进行增强后结果对比

实验2：选取复杂背景下的SAR图像，如图4a所示。经过CTGT方法增强后，由图4b可以看到，SAR图像中的一些非河流区域(建筑、桥梁)得到了一定的增强，但是还有一些原本亮度值相对较大的到了过度增强而且河流区域依旧没有得到增强。经过TFPSO方法增强后，由图4c可以看到，图像的整体细节都得到了一定的增强，包括河流区域。图4d为使用本文增强算法后所得图像，可以看到在图4c的基础上，增强效果又有了更进一步的提升，整体清晰度增加，可以清楚地看到图像中房屋分布、房屋界限以及桥梁区域等细节，这作为图像的预处理过程为之后桥梁、房屋区域的识别或分割等后续操作奠定基础。

图4 对SAR图像进行增强后结果对比

实验3：将本文算法用于过暗医学脑部MR图像增强。图5a为1幅过暗脑部图像，只能模糊的看到头骨、脑和脑室。经过CTGT方法增强处理后得到图5b图像，虽然头骨轮廓得到了增强，但是脑轮廓变得不再清晰。图5c为采用TFPSO方法对图像进行了增强，可以看到图像整体清晰度和对比度与原图相比有了很大的提高，不仅可以看到头骨、脑和脑室，还可以看到部分大脑灰质。在使用了本文算法对图像增强后，由图5d看可以看出图像头骨、脑和脑室变得更加清晰，可以清楚地观察到大脑灰质、脑镰结构和脑回走向，增强效果最好。

图5 对脑部MR图像进行增强后结果对比

3.2 数据对比

为了进一步体现本文方法对图像处理后的效果，将本文方法与其他两种方法对Lena图像、SAR图像和脑部MR图像分别增强后图像熵值结果进行了对比，结果见表1所示。

表1 图像增强后熵值对比

增强方法图像熵值LenaSAR脑部MR原图像(未处理)721602401CTGT增强729686519TFPSO增强749710547本文方法786762631

由表1可看出，使用本文方法对Lena图像、SAR图像和脑部MR图像进行增强后所得图像熵值均为最大，而且较原图像熵值相比分别增大9.20%、26.58%和57.36%。而使用CTGT增强方法和TFPSO增强方法后所得图像与原图像相比，图像熵值仅分别增大1.11%和3.88%、13.95%和17.94%、29.43%和36.41%。

在利用模糊算法对图像增强或与其他算法结合后对图像进行增强的过程中，模糊参数Fp、Fe的取值最优与否，对图像的增强后是否是最优效果起着极其重要的作用。因此，将本文方法与其他两种方法对lena图像、SAR图像和脑部MR图像进行增强后所求模糊参数Fp、Fe的最优值结果进行了对比，结果见表2所示。

表2 图像增强后模糊参数的最优值对比

增强方法LenaSAR脑部MRFeFpFeFpFeFpCTGT增强无无无无无无TFPSO增强123112771262本文方法184342382115473

由表2可看出，除CTGT增强方法不需要对模糊参数Fp、Fe求值以外，TFPSO增强方法和本文方法都获得了模糊参数Fp、Fe值。但是，TFPSO增强方法虽然可自适应的获得模糊参数Fp的值，却未考虑粒子群算法容易陷入局部最优的特点使得数值结果不够精确导致图像增强后质量不高，而且设置模糊参数Fe的值始终默认为1使得算法具有一定的使用局限性。本文方法通过提高粒子群优化算法的全局寻优能力以确保算法精度并防止重复寻优改善算法混合后的运算速度，而且采用二维粒子群优化搜索，同时得到了模糊参数Fp，Fe两个数值的最优值，因此数值结果较为精确、图像增强效果较好。

为了进一步证明本文方法的有效性，在算法检验后期，另外甄选出具有代表性的过暗SAR图像5幅，过暗医学MR头骨、胸骨、手骨、腿骨和脚骨这5种人体不同部位的过暗MR图像(各1幅)进行了增强操作。实验表明，通过本文方法处理后的过暗SAR图像、医学MR图像与原图像相比熵值分别平均增大24%以上、52%以上。

4 小结

本文针对图像在采集过程中所存在的模糊特性，在传统灰度变换增强算法的基础上，将模糊增强算法与粒子群优化算法相结合，提出一种基于二维粒子群优化的图像模糊增强算法。该算法可以在寻找模糊参数Fp、Fe的最优值过程中利用粒子空间对称分布原理，不断调整粒子位置，使粒子的位置尽量在模糊参数Fp、Fe的局部最优解周围而不只在其一侧，以减少粒子陷入局部最优情况出现，提高算法全局寻优能力；在搜索后期使用存储的禁忌表判断每次迭代时每个粒子是否有位置重复搜索，以避免粒子重复搜索，提高融合算法搜索效率。

通过实验验证，本文方法较好地解决了以往利用模糊算法对图像进行增强或与其他算法结合后对图像增强过程中所普遍出现的图像增强效果不理想、需要人为干预和算法精度低等问题。并且，本文方法可以对过暗SAR图像、医学MR图像进行增强操作，并且增强后图像效果较好。

[1] 仇国庆，龙毅，刘芙蓉.基于小波融合的人脸图像增强方法[J].电视技术，2014，38(11)：187-189.

[2] 赵杰，裴建英，门国尊.一种改进的图像去噪与增强模型[J]. 电视技术，2013，37(23)： 187-189.

[3] 朱秀昌，刘峰，胡栋. 数字图像处理与图像通信[M].北京： 北京邮电大学出版社，2002.

[4] 邸慧，于起峰，张小虎. 一种基于灰度变换的红外图像增强算法[J].应用光学，2006，27(1)：12-14.

[5] 龚昌来，罗聪，杨冬涛.一种改进的正弦灰度变换图像增强算法[J]. 电视技术， 2012， 36(13)： 60-63.

[6] 李均利，魏平，陈刚. 一种新颖的医学图像锐化增强算法[J]. 计算机工程与应用，2008，44(10)： 160-163.

[7] 陈延梅，吴勃英. 基于数学形态学的图像增强方法[J].哈尔滨工业大学学报，2006，38(6)：906-908.

[8] RUSSELL E，JAMES K. A new optimizer using particle swarm theory[C]//Proc.6th International Symposium on Micro-machine and Human Science.Nagoya，Japan： IEEE Press，1995：39-43.

[9] KAIDIRKAMANATHAN V， SELVARAJAH K， FLEMING P J. Stability analysis of the particle dynamics in particle swarm optimizer[J]. IEEE Trans. Evolutionary Computation，2006，10(3)：245-255.

[10] 黄洋文，王红亮.基于量子粒子群优化算法的图像分割方法[J]. 电视技术，2010，34(4)：16-18.

[11] 董宗然，周慧.禁忌搜索算法评述[J].软件工程师，2010(z1)：96-98.

[12] 仲晓敏，赵雪峰. 基于改进禁忌搜索算法的测试用例自动生成[J]. 计算机工程与设计， 2011，32(6)： 2058-2061.

[13] PAL S K，KING R A. Image enhancement using fuzzy sets[J]. Electronics Letters，1980， 16(9)：376-378.

[14] 叶志伟，常胜，高山.基于PSO的图像自适应模糊增强算法[J]. 湖北民族学院学报：自然科学版，2007，25(4)：415-419.

[15] 熊兴华. 数字图像质量评价方法评述[J]. 测绘科学，2004，29(1)：68-71.

白 冰(1990— )，硕士生，主要从事图像处理与模式识别方向的研究；

马 瑜(1974— )，博士，副教授，硕士生导师，主要从事计算机视觉与模式识别方向的研究；

杨晓丽(1991— )，女，硕士生，主要从事信号处理与模式识别方向的研究；

孟亚州(1991— )，硕士生，主要从事图像处理与模式识别方向的研究；

魏晶茹(1991— )，女，硕士生，主要从事图像处理与模式识别方向的研究。

责任编辑：时 雯

Research on Image Enhancement Algorithm Based on Fuzzy EnhancementOptimized by 2D Particle Swarm Optimization

BAI Bing1，MA Yu1，YANG Xiaoli2，MENG Yazhou1，WEI Jingru1

(1.GraduateSchoolofNingxiaUniversity，Yinchuan750021，China；2.NingxiaKeyLaboratoryofIntelligentSensingforDesertInformation，Yinchuan750021，China)

Aiming at the phenomenon of classic image enhancement method based on grayscale transformation method which is vulnerable to image quality， researching for the particle swarm optimization and fuzzy enhancement algorithm that an image enhancement algorithm based on fuzzy enhancement optimized by 2D particle swarm optimization is proposed which combined with tabu search and particle spatial distribution principle. In this algorithm， adjusting the particle distribution for spatial distribution of symmetry to avoid the algorithm falling into local optimal and improve the global search ability， and adding tabu search algorithm in traditional particle swarm optimization in order to reduce the duplication optimization of particles and improve the searching efficiency of the algorithm by recording the position of the particle search in the later of iteration.Finally， the particles’ search position and velocity update direction of the improved particle swarm optimization algorithm are setted to the 2D and combined with fuzzy enhancement algorithm that can adaptive search the optimal value of fuzzy parametersFpandFeto achieve fuzzy enhancement. The experiments show that the improved algorithm is better for image enhancement and can effectively improve the image quality when used for SAR image and medical MR image enhancement that are too dar.

2D particle swarm optimization； symmetry spatial distribution of particle； tabu search； fuzzy enhancement； adaptive optimization

宁夏回族自治区科技攻关计划项目(2012ZYG011)

TP391.41

A

10.16280/j.videoe.2015.19.005

2015-06-25

【本文献信息】白冰，马瑜，杨晓丽，等.基于二维粒子群优化的图像模糊增强算法研究[J].电视技术,2015，39(19).