最小移动二乘抠图

王 洁，沈 洋，包艳霞，谢志峰，林 晓

(1.丽水学院工学院，浙江 丽水 323000；2.上海交通大学 计算机科学与工程系，上海 200240；3.洛阳师范学院 计算机科学与工程系，河南 洛阳 471022)

最小移动二乘抠图

王 洁1，沈 洋1，包艳霞1，谢志峰2，林 晓3

(1.丽水学院工学院，浙江 丽水 323000；2.上海交通大学 计算机科学与工程系，上海 200240；3.洛阳师范学院 计算机科学与工程系，河南 洛阳 471022)

交互式抠图技术在有限的用户交互下抠取图像的前景，被广泛地应用在图像及视频编辑、三维重建等领域中，有极高的应用价值。近年来的抠图技术中，拉氏矩阵给出alpha图上像素间的线性关系，对alpha图的估计起到了重要作用。提出了一种改进拉普拉斯矩阵的方法，使用移动最小二乘法替代最小二乘法，结合最近邻(KNN)方法给出移动拉氏矩阵，并使用移动拉氏矩阵计算alpha图。实验结果证明了移动拉氏矩阵的有效性。

图像抠图；拉氏矩阵；最小移动二乘

交互式抠图是在有限的用户交互下，计算前景的alpha图，从而将前景从背景中分离出来。抠图问题的输入是原图像I和用户提供的三分图，输出是alpha图及前景F、背景B，因此是典型的病态问题，需要引入假设条件求解alpha图。

抠图算法可分为3类：基于采样的方法、基于传播的方法、采样和传播结合的方法。其中，基于传播的方法有着举足轻重的作用，Levin等根据局部线性模型[1]推导出的拉氏矩阵给出邻域像素的alpha值间的线性关系，被广泛应用在抠图算法中。拉氏矩阵有其局限性，拉氏矩阵表示空间邻域内像素间的关系，但不能体现非邻域间像素间的关系。拉氏矩阵建立在空间连续的假设基础上，在某些前景和背景分量突变的区域，拉氏矩阵难以得到理想的效果。

本文提出一种改进的拉氏矩阵计算方法，使用最小移动二乘法替代最小二乘法推导出移动拉氏矩阵。相对于最小二乘法，移动最小二乘法求解的线性条件更为准确。笔者使用KNN邻域替代空间邻域，使得拉氏矩阵可以反映非邻域间像素的alpha值的关系。试验结果表明本文方法是有效的。

1 相关工作

早期的抠图算法例如贝叶斯抠图基于颜色空间上的采样，对任意未知像素，基于采样的方法在三分图的已知前景和背景区域中寻找最优的前景和背景对匹配当前像素，像素对应的alpha值与像素的空间位置无关，该类方法不能保持alpha图的空间连续性。在前景和背景颜色混杂时，未知像素可能和多个的前景背景颜色匹配，导致生成错误的alpha图。近年来发展的基于采样的方法如共享式采样[2]假定在小邻域内前背景分量一致。共享式采样为了保证结果的光滑性，并提高正确率，改进了信任度计算方法，并对结果进行多次平滑操作，

Rajan等人[3]提出了颜色及纹理采样方法，不仅考虑到了像素的信息，还考虑纹理的信息，从而使得采样更为可靠鲁棒。但基于采样的方法不能很好的保证alpha图在空间上的连续性，也不能有效的利用空间连续性计算alpha图，不同于基于采样的方法基于传播的方法充分考虑相邻像素间的空间关系，基于传播的方法构造像素在alpha图上的关系，alpha值的求解类似于alpha值从已知区域向未知区域传播的过程，例如如泊松抠图、随机游走抠图[4]、闭形式抠图[1]等。

由于抠图问题是典型的病态问题，因此需要alpha图满足一定的假定条件才可求出唯一解，例如泊松抠图假定像素对应的前景分量和背景分量是光滑的，在此基础上闭形式算法使用，并由此给出相邻像素间alpha图的变化信息。闭形式抠图假定像素对应的前景分量和背景分量在局部小邻域内是不变，从而根据局部线性假设得到alpha值在局部邻域空间上的线性关系，从而以拉氏矩阵的形式给出alpha图在空间上的关系。旧的传播方法如泊松抠图随机游走抠图需要调整局部或全局参数，相比之下，闭形式方法不需要调整参数且效果更佳，因此被广泛的应用的现有的抠图算法中。

闭形式抠图方法需要求解大型稀疏线性方程，因此效率不高。闭形式方法由于基于小邻域下的传播模型，在某些前背景分量无法传播到的区域无法取得良好的效果。何凯明等提出了大核抠图方法[5]，何等发现拉氏矩阵在大核情况下运用共轭梯度法求解收敛更快，而且大邻域可以覆盖更多的前景和背景区域，从而可以传播更多的前景和背景分量，从而在某些有洞的区域得到较好的效果。大核方法假设内像素的alpha值在相对较大的邻域内保持线性关系，其假定条件对比于小核更不易成立，因此在复杂纹理处效果不佳。Zheng等人[6]提出了基于学习的抠图方法，将局部线性模型扩展为局部非线性模型，从而在非线性关系下也能取得较好的效果。

由于闭形式方法获取邻域上像素的alpha值关系，本质上属于邻域方法，不能获取像素在非邻域上的关系。近几年的基于传播的方法侧重于从非邻域上获取alpha值的关系，Lee等人[7]提出了非邻域抠图方法，从非邻域方法构造拉氏矩阵。KNN(K Nearest Neighbor)方法[8-9]使用KNN邻域替代空间邻域。Chen等则提出了邻域和非邻域结合[10]的方法，该方法假定alpha图能保持图像空间上的流形结构，从而得出alpha图在图像流形上的非邻域结构关系，再和邻域上的拉氏矩阵结合，从邻域和非邻域二个方面得出新的传播模型。

拉氏矩阵在图像编辑中有大量的应用[11-12]，从现有的抠图方法来看，闭形式对应的拉氏矩阵仍然在现有抠图方法中起到重要的作用，而抠图方法在一系列应用中有着基础性的应用价值[13-14]。本文使用KNN邻域替代空间邻域，从而可以获取非邻域像素在alpha图上的线性关系，并用移动最小二乘替代最小二乘，从而计算出移动拉氏矩阵，并得到alpha图，实验结果表明移动拉氏矩阵更为有效。

2 最小移动二乘抠图

闭形式方法基于局部线性假设，表示如下

αi=aIi+b,i∈wi

(1)

当局部邻域内假设条件不成立时，特别是邻域比较大且纹理复杂的情况下效果不佳。假设在邻域内alpha值满足线性条件，不同于闭形式方法[1]使用最小二乘法求解局部线性关系，在窗口wi内使用移动最小二乘法求解局部线性关系，表示如下

(2)

(3)

与闭形式抠图不同处在于：在最小化式(2)和式(3)中增加了权值ω，移动最小二乘在距离当前像素越远的地方权值ω越小，因此移动最小二乘法能求解出更准确的局部线性关系，比最小二乘法求解的线性关系更为有效。ωi是邻域wk中的权值。式(2)和式(3)可以表示为以下矩阵的形式

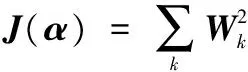
(4)

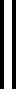
系数ak，bk求解如下

(5)

(6)

(7)

(8)

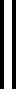
2.1 彩色模型下的移动最小二乘抠图

彩色模型下类似于闭形式算法， 用式(9)表示彩色图像各通道间的线性关系

(9)

式中：c为彩色图像的通道数，在考虑各个通道信息后，式(2)和式(3)转化为

(10)

对式(10)进行化简后，解得彩色模型下移动拉氏矩阵如下

J(α)=αLαT

(11)

(12)

式中：I为小邻域内所有像素对应3×1颜色向量组成的矩阵；μk为I的Wk加权平均；Σk是I在Wk加权下的协方差矩阵。

2.2 KNN邻域

由于拉氏矩阵不能反映像素的非邻域关系， 在此借鉴KNN抠图引入KNN邻域，将拉氏矩阵中的空间邻域扩展到KNN邻域，KNN空间的点由(R，G，B，X，Y)五维共同决定。使用KD-TREE实现KNN邻域的高效查找。由于KNN邻域反映空间非邻域上像素间的关系。因此本文方法结合了非邻域抠图的优点。

3 移动二乘抠图中的大核求解

由于移动抠图算法中，设核的大小为r，图像像素个数为imagesize，存储拉氏矩阵L所需要的空间复杂度为imagesize×r2，计算空间复杂度随着核的增大而急剧增大。借鉴大核方法中[5]的计算技巧，使用改进的共轭梯度法求解alpha值。

对于方程Lx=b，共轭梯度法的关键在于构造共轭向量p，并求其对应的残差。共轭梯度法可以用迭代方法求解。在每次迭代过程中，新共轭向量由求解如下

(13)

共轭方向的系数求解如下

(14)

新的x值与残差用求解如下

xk=xk-1+skpk

(15)

rk=rk-1+skLpk

(16)

在共轭梯度求解过程中关键的步骤在于求解向量Lp，直接求解L的空间复杂度过大，但Lp的维数为imagesize，因此需要避免直接求解L，而直接用下式求解Lp向量中点i对应的元素qi

(17)

(18)

(19)

(20)

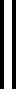
(Lp)i计算公式的正确性由以下定理保证：

定理1：式(17)计算得出的(Lp)i与利用式(12)计算出的(Lp)i是等价的。

证明：

令q=Lp，由于q与p为线性关系，因此只需要证明式(21)

(21)

(22)

此外，有

(23)

根据式(18)，并对pj做偏导，可得

(24)

将式(23)和式(24)代入式(22)，可得到

(25)

式(25)即式(12)中对应的拉氏矩阵L。

4 实验结果

当前的抠图方法中，大多使用了基于传播和基于采样结合的方式提高算法的准确性，在此将最常见的几种传播方法：闭形式方法、KNN方法、基于学习的方法、大核方法进行了比较。

从图1可知，闭形式算法对细节处理较好，由于其传播模型只考虑到了空间小邻域间的信息，而Doll毛发附近的字符间有间隔，是空间上的非邻域关系，因此alpha值不能在字符间顺利传播，也无法干净的抠除这些字符。在plant图中，由于植物树叶间的空洞与三分图中的背景分量并没有空间上的邻域关系，因为闭形式方法同样难以将背景分量传播至植物中的空洞中。

图1 不同算法比较

在大核方法中，由于传播模型在相对较大的邻域内进行传播。在大核情况下，毛发附近的字符是邻域关系，因此算法成功的抠除了毛发附近的字符，但由于植物树叶间的空洞与背景空间距离较远，所以大核仍然无法解决植物中的空洞问题。此外，局部线性假设不易在大核时成立，因此算法对复杂纹理处理的效果不好。

由于KNN方法建立在非邻域的基础上，因此KNN方法可以在非邻域上进行alpha值的传播。KNN方法因此可以在植物的空洞以及Doll毛发附近的字符处取得良好的效果。

相对于闭形式方法，KNN方法对应的拉氏矩阵建立在全局统一的参数基础上，因此细节处理不好。在Doll图片中，KNN方法使得毛发周围较为模糊，不能较好地提取毛发，毛发左边的英文字母也没有清除干净。在plant图中算法在叶子周边没有抠除干净。在Plastic bag图片中，KNN方法同样在绳子附近留下大量噪声。而本文方法在Doll周边的毛发处理较为干净，特别是英文字符全部被干净的清除，在Plastic bag中，绳子附近处理也较为干净。Tree图中在有洞的区域同样得到较好的效果。从表1的参数可以看到，net图中的方法效果明显好于其他方法，由于net图中的未知区域非常大，而本文方法提供了更为准确的拉氏矩阵，因此得出了较好的结果。

表1 主要抠图方法性能对比

算法SADTrollDollElephantPlantPlasticbagNet闭形式方法1727767370135731333350大核方法1990840510118030303417学习方法1890710290138322404143KNN方法1757930480106018233347MLS方法186393039098018932027

[1] LEVIN A，LISCHINSKI D， WEISS Y. A closed form solution to natural image matting[C]//Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Los Alamitos：IEEE Press，2006：61-68.

[2] GASTAL E S L，OLIVEIRA M M. Shared sampling for real-time alpha matting[J]. Computer Graphics Forum，2010，29(2)：575-584.

[3] SHAHRIAN E，RAJAN D，PRICE B，et.al. Improving image matting using comprehensive sampling sets[C]//Proc. IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos：IEEE Press，2013：636-643.

[4] GRADY L，SCHIWIETZ T，AHARON S，et.al. Randomwalks for interactive alpha-matting[C]//Proc. 5th IASTED International Conference on Visualization，Imaging and Image Processing. Calgary：ACTA Press，2005：423-429.

[5] HE K M，SUN J，TANG X O. Fast matting using large kernel matting laplacian matrices[C]//Proc. IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos：IEEE Press，2010：2165-2172.

[6] ZHANG Z P， ZHU Q S， XIE Y Q，Learning based alpha matting using support vector regression[C]//Proc. 19th IEEE Conference on International Image Processing. Los Alamitos：IEEE Press，2012：2109-2112.

[7] LEE P，WU Y. Nonlocal matting[C]//Proc. IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos：IEEE Press，2011：2193-2200.

[8] CHEN Q F， LI D Z Y， TANG C K. Knn matting[C]//Proc. IEEE CVPR (2012). Los Alamitos：IEEE Press，2012：869-876.

[9] 沈皓.基于改进KNN算法的AVS到H.264/AVC 快速转码方法[J].电视技术，2015，39(8)：35-39.

[10] CHEN X W， ZHOU D Q， ZHOU Z Y， et.al. Image matting with local and nonlocal smooth priors[C]//Proc. IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos：IEEE Press，2013：1902-1907.

[11] HE K M， SUN J，TANG X O. Guided image filtering[C]//Proc. 11th European conference on Computer vision. Aire-la-Ville：Eurographics Association Press，2010：1-14.

[12] 蔡宇文，盛斌，马利庄.优化分割的手绘图像彩色化技术[J].计算机辅助设计与图形学学报，2013，25(6)：774-781.

[13] 卢胜男，段沛沛，冯建利，等.基于块匹配置信度的隧道交通背景提取算法[J].电视技术，2015，39(8)：59-63.

[14] 杨如林，丑修建，李庆，等.一种快速鲁棒的红外图像分割方法[J].电视技术，2015，39(3)：11-15.

责任编辑：时 雯

Moving Least Square Matting

WANG Jie1，SHEN Yang1，BAO Yanxia1，XIE Zhifeng2，LIN Xiao3

(1.InstituteofTechnology，LishuiUniversity，ZhejiangLishui323000，China；2.DepartmentofComputerScienceandEngineering，ShanghaiJiaoTongUniversity，Shanghai200240，China;3.AcademyofInformationTechnology，LuoyangNormalUniversity，HenanLoyang471022，China)

Interactive alpha matting technique extracts the foreground of image with limited interaction. It is widely applied to image editing，3D construction，and has high applicative value.In recent years，the Matting Laplace matrix gives the linear relation on alpha matte，and takes important roles in alpha matting. In this paper， the Moving Matting Matrix is given， which use moving least square instead of least square method， use KNN(K nearest neighbor) model instead of local neighbor model. We solve the alpha matte by Moving Matting Matrix. Experiments prove this method is effective.

image matting； matting laplace matrix； moving least square

浙江省自然科学基金面上项目(LY13F020019)；国家自然科学基金重点项目(61133009)；浙江省大学生科技创新活动计划项目(新苗人才计划)(2013R429004)

TP391

A

10.16280/j.videoe.2015.19.006

王 洁(1992— )，女，本科，研究方向为计算机视觉及仿真；

沈 洋(1975— )，博士，讲师，本文通讯作者，研究方向为动画制作、图像处理、虚拟现实；

包艳霞(1980— )，女，硕士，研究方向为计算机仿真；

谢志峰(1982— )，博士，研究方向为图像及视频编辑、计算机视觉、数字媒体技术；

林 晓(1978— )，女，博士，副教授，研究方向为视频编辑、计算机视觉、数字媒体处理。

2015-02-22

【本文献信息】王洁，沈洋，包艳霞,等.最小移动二乘抠图[J].电视技术,2015，39(19).