条件函数依赖的增量计算

刘 波，周健昌

（暨南大学信息科学技术学院，广东广州510632）

条件函数依赖的增量计算

刘 波，周健昌

（暨南大学信息科学技术学院，广东广州510632）

条件函数依赖是对传统函数依赖的扩展，它通过引入条件模式，使其语义比函数依赖更精确、表达能力更强。然而，条件函数依赖的计算需要消耗较多的时间，为了提高条件函数依赖挖掘的效率，研究了条件函数依赖增量维护方法。针对数据集增加、删除、修改3种情况分别分析了条件函数依赖集变化规律，提出了条件函数依赖的增量计算算法，从而能够在数据库变化情况下，高效、动态地维护条件函数依赖。同时，在理论上对算法中关键步骤的正确性进行了论证，并通过实验验证了算法的有效性。

增量计算；条件函数依赖；数据挖掘

0 引 言

传统的函数依赖（functional dependencies，FDs）主要用于数据库模式设计，但对于刻画数据值的特征还不够精确，其语义约束过于严格而往往脱离现实情况。Bohannon P等在FDs的基础上，通过引入“条件模式”［1］，放宽了这种约束，形成条件函数依赖（conditional functional dependencies，CFDs）（在下文中，CFD表示一条条件函数依赖，CFDs表示多条条函数依赖），从而使描述的语义信息更精确，能够表达在局部范围内成立的函数依赖。

目前对FDs及CFDs的研究主要都是基于静态数据集的。算法TANE［2］和算法Fast FDs［3］是最具代表性的FDs挖掘方法。近些年，在CFDs挖掘方面，也提出一些卓有成效的算法，如Fan W F等提出了3个发现最小CFDs集的算法［4］：①CFDMiner，用基于闭数据项集的挖掘方法，挖掘常量CFDs；②CTane，基于层次的算法，是对算法TANE的扩展；③FastCFD，基于深度优先的策略，是对算法Fast FD的扩展。文献［5］、文献［6］分别研究了频繁常量CFDs、近似CFDs的发现方法。此外，在CFDs应用方面的研究主要集中在数据清洗与重复检测方面，如文献［7- 13］。

但是，数据库往往是变化的，因而CFDs也应随之更新。至今，未见基于变化数据更新CFDs的研究，相关的增量处理方法与本工作研究目标不同。文献［14］研究的主体是FDs，而且针对插入元组采用增量方法计算FDs，但基于删除元组采用非增量方法计算FDs。文献［8］介绍了CFDs在违例元组的增量检测方面的应用，即在CFDs集保持不变的情况下，针对插入、删除、修改元组增量检查是否有违例元组出现。

本文主要创新点如下：①基于非增量计算算法CTane，针对数据表的增加、删除、修改元组等不同操作，分别分析了在相应情况下CFDs变化规律；②提出了增量计算CFDs算法CTane-IncProc，且分析并验证了此算法的正确性与高效性。该研究工作与其他CFDs相关研究目标与方法不同，例如，文献［4］主要研究非增量计算CFDs的方法，而本文针对变化的数据集研究增量计算方法。

1 问题描述与相关概念

1.1 问题描述

假设给定关系模式R的关系数据表r，且：

Δr：对r进行的增量操作元组集；

r′：增量操作发生后新关系数据表；

Partitions（r）：增量操作发生前r的划分信息；

CFDs_old（r）：数据表r更新发生前的最小条件函数依赖集；

CFDs_new（r）：数据表r更新发生后的最小条件函数依赖集。

CFDs增量计算问题描述为：

给定：数据表r，由CTane算法［4］得到的最小条件函数依赖集CFDs_old（r），划分信息Partitons（r），以及增量操作元组集Δr。

目标：增量计算变化后的数据表r′中最小条件函数依赖集CFDs_new（r）。

难点：

（1）如何保证CFDs_new（r）中的条件函数依赖是最小的；

（2）如何保持增量挖掘过程中的辅助信息的一致性状态，使得这种增量计算不会引入错误，从而可以持续地用更新后的信息再进行下一次的增量挖掘。

1.2 相关概念

在下文中，R表示关系的模式；r为R的关系数据表；A、B、X、Y、Z分别为R的一个属性或属性集合；attr（R）表示R的全体属性集；Dom（A）表示r中属性A的值域。

定义1CFD［4］：

R上的某CFD可以表示为

式中，X⊆attr（R），Y⊆attr（R）；X→Y是一个标准FD；tp［X∪Y］为定义在X∪Y上的模板，若A∈X∪Y，tp［A］为属于Dom（A）的常量或变量值“－”。

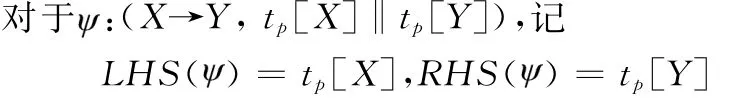
设Y＝A1∪A2∪…∪An，根据阿姆斯特朗公理中的合并律，任何形式为（X→Y，tp［X］‖tp［Y］）的CFD都可由（X→A1，tp［X］‖tp［A1］）、（X→A2，tp［X］‖tp［A2］）、…、（X→An，tp［X］‖tp［An］）合成，故本文只讨论并挖掘形式为（X→A，tp［X］‖tp［A］）的CFD，其中A仅包含一个属性，这简化了算法的复杂性。

定义2常量CFD、变量CFD［4］：

在CFD：（X→Y，tp［X］‖tp［Y］）中，tp［X∪Y］中不含变量“－”，则称为常量CFD，否则就是变量CFD。

例如，按CFD的定义，从表1可得如下CFDs：

其中，1和2是变量CFDs，3是常量CFD。

表1 数据集示例

定义3模板间的泛化关系［4］：

为模板的变量值与常量值定义出一个关系符“≪”，称泛化。有如下两种泛化：

（1）属性值的泛化：∀A∈attr（R），若n1、n2∈tp［A］且n1＝＝n2或n1是常量而n2是变量，则有n1≪n2；

显然，泛化程度的高低体现的是模板抽象、概括能力，即语义包含能力。泛化程度低的模板所蕴含的元组也必被泛化程度高的模板所蕴含。

定义4等价类［4］：

属性集X的某一等价类［t］X是指在给定关系实例中，所有与元组t在X上取值对应相等（简称与t在X上取值相等）的元组的集合。

定义5划分［4］：

在TANE算法中，划分πX被定义为X的所有等价类的集合。在CTane中扩展划分定义π（X，SP）：是πX中比SP具体化的所有模板所包含的等价类集合，即π（X，SP）是符合SP约束的πX的子集。

定义6平凡CFD［4］：

定义7左归约CFD［4］：

定义8最小CFD［4］：

例如，考虑如下CFD：

因存在（（Major）→（College），（－）‖（－）），所以4不是最小CFD。

本文研究的CFD计算即指最小CFD的计算。

2 CFDs集的增量计算

由于不同类型的增量操作对最小CFDs集的影响是不同的，因此增量计算最小CFD需要按操作类型分别研究。

表2是对表1的增量操作示例表，有如下特点：

（1）在属性方面表2比表1多两个字段：ID字段取值OPi表示第i个增量操作；OP字段表示增量操作的类型，其取值DEL表示删除，INS表示增加，UPD表示修改元组。

（2）修改元组中的某些字段值，如“C，D”，表示将值C修改为值D。

（3）ID、TID字段仅是为方便描述而附加的字段，挖掘与更新均不涉及。

表2 增量操作示例表

2.1 新增元组与CFDs的增量计算

新增元组可能使原有CFDs失效，也可能导致原有CFDs仍然有效、或新增CFDs。

2.1.1 原有CFDs失效及有效的情况定理1在关系r中插入元组t，若

且在r＼｛t｝中存在t′，使t′［X］＝t［X］≪tp［X］，t′［Y］≠t［Y］，则∉CFDs_new（r）。

定理1可根据CFD的定义以及模板泛化的概念直接证得，这也是插入一个元组后判断一条CFD是否成立的依据，插入的元组t若符合定理1中的条件，则失效。

例如，表2中的OP1操作后，原有的CFD：（（Group）→（Name），（A）‖（曾莉）），因符合定理1的条件而失效，故不应加入CFDs_new（r）。

反过来看上述定理1，可得以下推论。推论1在关系r中插入元组t，若

（1）∀t′∈r＼｛t｝，t′［X］＝t［X］≪tp［X］，且t′［Y］＝t［Y］≪tp［Y］；

（2）在r＼｛t｝中不存在t′，使t′［X］＝t［X］≪tp［X］，而不论t′［Y］取何值。

例如，表2中的OP1操作后，（（Group）→（Major），（A）‖（通信））显然因为符合条件（1）而保留。（（Group，Gender）→（Major），（A，－）‖（－））、（（Group，Gender）→（Name），（A，－）‖（－））都因为t7［Group，Gender］有新取值（A，Male）而保留，而不管t7［Major］、t7［Name］取何值。

2.1.2 新增CFDs的情况

插入一个元组不但可能会使CFDs失效，还可能会生成一些CFDs_old（r）中不存在的CFDs，即：（X→Y，tp［X］‖tp［Y］）∉CFDs_old（r），但∈CFDs_new（r）。具体情况如下：

（1）在r＼｛t｝中∃t′，使t′［X］＝t［X］≪tp［X］，t′［Y］＝t［Y］≪tp［Y］，且满足这一条件的元组t′个数之和为k－1（k是CTane算法中设置的频繁度阈值），而插入t后（t′［X］‖t′［Y］）的频繁度达到k，故应将插入到CFDs_new（r）；

在上述情况中，情况（1）是量的积累达到频度k，从而新的CFD被检测到；情况（2）是因为插入元组使泛化程度更高的′向低泛化的退化，且基于′产生多条。

例如，对于表2中的OP1，存在泛化退化的情况：在插入前存在的：（（Group，Major）→（Name），（－，－）‖（－）），由于插入t7后，对于满足［Group，Major］＝（A，通信）的两个元组t1与t7，在［Name］上取值不相同，所以不再成立，但它可以分解为以下泛化程度较低的CFDs：

2.1.3 最小CFDs集的更新

根据以上情况的分析，本研究采用以下方法对最小CFDs集进行更新。

假设新插入元组为t，r为修改前的新数据表，对CFDs_ old（r）中的每艘最小CFDs：（X→Y，tp［X］‖tp［Y］）进行如下检测：

依据推论1中的条件（2），如果t在X的任一分量上出现新属性值，则满足在r＼｛t｝中不存在t′，使t′［X］＝t［X］≪tp［X］，所以仍是最小CFD。

（2）若r′＝｛t′｜t′∈r，t′［X］＝t［X］｝为空，则t对无影响，将加入到CFDs_new（r）。

因为r′＝｛t′｜t′∈r，t′［X］＝t［X］｝为空，说明在t插入前，r中没有以t［X］为X属性值的元组，依据最小CFD的定义，t对无影响，所以仍是最小CFD。

（3）若r′＝｛t′｜t′∈r，t′［X］＝t［X］｝非空，且存在t′∈r′，使t′［X］＝t［X］≪tp［X］，但t′［Y］≠t［Y］，则：

2.2 删除元组与CFDs的增量计算

删除元组可能使原有CFDs仍然有效或无效或新增CFDs。

2.2.1 原有CFDs失效及有效的情况

定理2关系模式为R的实例r中，删除其中任一元组t，对CFD：（X→Y，tp［X］‖tp［Y］）而言，若删除t后，tp［X∪A］的频度仍满足频度k，则是有效的，否则是无效的。

证明假设删除的是r中的元组t，则删除后的关系为r′＝r＼｛t｝，r′′＝｛t′′｜t′′［X］≪tp［X］，t′∈r′｝。在删除t后，tp［X∪Y］仍满足频度k时，在r中成立，即∀t1、t2∈r，t1≠t，t2≠t，只要t1［X］＝t2［X］≪tp［X］，必有t1［Y］＝t2［Y］≪tp［Y］。很显然，r′′⊆r′⊂r，故在r中成立，当然在r的子集中r′也成立。即r′中的任意两个元组只要符合t1［X］＝t2［X］≪tp［X］必有t1［Y］＝t2［Y］≪tp［Y］，故而仍成立。

若tp［X∪Y］的频度在删除元组后达不到k，则失效。

证毕

例如，对于表2中的OP2，（（Group，Major）→（Name），（－，－）‖（－））仍然是有效的（假设仍满足k阈值），因为更新后的表r′中，除被删除元组外，任意两条元组都在更新前的表r中，它们也当然遵守在r中的规则。

2.2.2 新增CFDs的情况

在数据表r中删除元组t可能使原来不属于CFDs_old（r）中的某CFD：（X→Y，tp［X］‖tp［Y］）成立，因为在r中，若只有t违反了取值为tp［X］、Y取值为tp［Y］的约定，则删除t后，∀t1、t2∉r′，只要t1［X］＝t2［X］≪tp［X］，必有t1［Y］＝t2［Y］≪tp［Y］。然而，由于CFDs_old（r）、CFDs_new（r）均要求是最小条件函数依赖集，所以情况有些复杂。

例如，在表2中的OP2操作前，表1中只有t1与t2的取值冲突使1：（（Gender，College）→（Group），（－，信息学院）‖（－））及2：（（Gender，College）→（Group），（Female，－）‖（－））不成立，删去t1后应该增加1及2，然而由于在操作前已存在以下CFDs：

2.2.3 最小CFDs集的更新

据上面讨论的情况，设删除的元组是t，删除t后的关系为r，使用以下方法对最小CFDs集进行更新：

（1）检测因删去t而新生成的CFDs，并加入到CFDs_ new（r）中。新生成的CFDs可能是CFDs_old（r）中已有CFDs的更泛化版本（原CFDs虽仍成立，但已不是最小的），也可能是原CFDs_old（r）根本没有涉及到的新CFDs。

这种情况需要采取启发式的重新挖掘方法产生最小CFDs，在非增量的CTane算法中利用一些剪枝策略提高效率。

依据定理2，可以证明：若tp［X∪Y］的个数仍达到频度k，还是最小CFD。

（3）在CFDs_new（r）中合并相应可合并的CFDs，从而保证CFDs_new（r）中的CFD集是最小的，形成最终状态的CFDs_new（r）。

依据第2.2.2节分析的新增CFD情况，经过一系列模板合并成更泛化的模板可以产生最小CFD。

删除更新的真正难点在于（1）的处理，这里采取启发式的重新挖掘方法。首先修正划分信息，再在重新挖掘时借助CFDs_old（r）中的CFDs作指导，尽早剪去无用的Lattice［15］分枝，从而有针对性地重新挖掘，加快挖掘效率。重新挖掘可利用的剪枝策略包括：

（1）对已判断为主键或FD的属性集／模板结点提前剪枝，甚至根本不生成这样的结点。

（3）只检测常量模板的Lattice结点。

例如，针对上一例子，在表2中的OP2操作后，直接生成1：（（Gender，College）→（Group），（－，信息学院）‖（－）），与1′：（（Gender，College）→（Group），（－，数学学院）‖（－））合并生成：（（Gender，College）→（Group），（－，－）‖（－）），然而，也可以只检测加入常量的CFDs，θ1：（（Gender，College）→（Group），（Female，信息学院）‖（计算机））、θ2：（（Gender，College）→（Group），（Male，信息学院）‖（通信）），再由θ1与θ2合并成1，最后由1与已存在的1′合并成。

这种操作似乎由于增加合并操作而降低了效率，但在重新挖掘过程中，只生成判断tp［X∪Y］全为常量的结点，不但减少了分枝的数目，而且使整体过程的复杂性有较大的降低。因为CTane算法操作的复杂性很大一部分是因为要处理变量模板，而相对来说，CFDs的合并操作尽管有一个循环反复的过程（如上述例子中，θ1与θ2合并成1，再由1与已存在的1′合并成），但时空复杂性并不会太高，故而总体效率不但没有降低，反而有所提升。

在计算最小CFDs的过程中，还可以节省大量的计算，因为保留着划分信息，从而可以避免重新扫描数据集带来的巨大开销，同时剪枝策略只处理常量模板，所以算法时间代价有较大程度的降低。

2.3 修改元组与条件函数依赖的增量计算

对数据表元组进行更新的操作实质上都可以拆分成两个操作的叠加：

删除原元组：（a1，b1，c1，…，n1）；

插入新元组：（a2，b2，c2，…，n2）。

因而，更新一条元组引起对CFD集的修改，可采用上面所述的增加一条元组和删除一条元组引起CFDs集修改的方法。

2.4 划分的维护

无论因插入操作使tp［X∪Y］刚达频度k还是因删除操作使tp［X∪Y］刚好不足频度k（本文统称两种频度的变化为频度临界变化），都会涉及到的一个问题：对：（X→Y，tp［X］‖tp［Y］）而言，tp［X∪Y］的频度需要维护，而这个问题归根结底是CTane算法结束后对划分的增量维护，实质上，就是属性集X上的等价类维护。在数据集变化的同时，标记发生频度临界变化的tp［X∪Y］，可以更有针对性地判断新产生或删去哪些CFDs。

当划分信息更新完成后：

（1）针对删除操作，对发生频度临界变化的tp［X∪Y］，从CFDs_new（r）中删除：（X→Y，tp［X］‖tp［Y］）。

（2）针对插入操作，对发生频度临界变化的tp［X］，∀A∈X，Y＝X＼｛A｝判断（Y→A，tp［Y］‖tp［A］）是否成立，若成立则加到CFDs_new（r）中。

例如，取X＝（Group，Major），Y＝（Name），tp［X］＝（－，－），tp［Y］＝（－），在表2中的插入操作OP1前，关于X的划分信息为π（X，tp［X］）＝｛｛t1｝、｛t2｝、｛t3｝、｛t4｝、｛t5｝、｛t6｝｝、π（X∪Y，tp［X∪Y］）＝｛｛t1｝、｛t2｝、｛t3｝、｛t4｝、｛t5｝、｛t6｝｝，由于π（X，tp［X］）与π（X∪Y，tp［X∪Y］）的划分信息是一致的，所以：（X→Y，tp［X］‖tp［Y］）成立；在插入操作OP1后，π（X，tp［X］）＝｛｛t1，t7｝、｛t2｝、｛t3｝、｛t4｝、｛t5｝、｛t6｝｝、π（X∪Y，tp［X∪Y］）＝｛｛t1｝、｛t2｝、｛t3｝、｛t4｝、｛t5｝、｛t6｝、｛t7｝｝，则π（X，tp［X］）与π（X∪Y，tp［X∪Y］）有不一致的划分，所以不再成立。

类似地，删除时，就在各个相关的等价类中删除元组信息即可。

2.5 CTane-IncProc算法

根据上述CFD增量计算的思路，基于CTane算法，本节提出了最小CFD的增量计算算法CTane-IncProc。

输入R，r，Δr，Partitions，CFDs_old（r）

输出CFDs_new（r）

2.6 算法复杂度

CTane-IncProc算法的时间复杂度可通过对如下两个主要过程分析获得［16］。令：｜r｜为数据集的元组数目，｜R｜为数据集包含的属性数目，f为attr（R）中属性的平均取值数目。

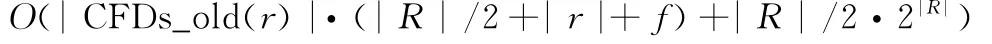
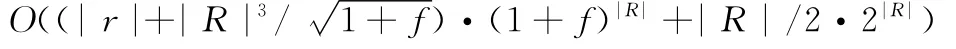
CTane-IncProc的空间复杂度为

虽然从理论上分析，CTane-IncProc算法在最坏情况下并没有降低CTane算法的复杂度，但采用增量计算的CTane-IncProc算法，由于有CFDs_old（r）及增量操作的启发，使得搜索空间要小于CTane算法需要的搜素空间，从而实际性能要优于CTane算法，从第3节的实验结果可以得到验证。

3 实验结果

3.1 实验数据与环境

在实验过程中，主要用到UCI（http：∥archive.ics.uci.edu／ml／datasets／）公开数据集，此外，也用到由开源数据生成器Spawner产生的数据集。实验数据集如表3所示，其中，｜R｜表示数据集中的属性数目，｜r｜表示数据集中的元组数目。

所有实验在Red Hat Enterprise Linux 6.1（Kernel 2.6.32）、CPU Intel Pentium E2180 2.0GHz×2、内存2.0GB的微机环境下，采用CodeBlocks 10.05开发工具及C＋＋编写软件完成。

表3 实验数据集

3.2 实验结果及分析

实验中，主要参数为：｜r｜、｜R｜、｜CFDs_old（r）｜、频繁度阈值k等。采用CTane与CTane-IncProc两种算法分别针对表3中的数据集进行了实验，产生的最小CFDs都是一致的，但两种算法的时间性能不同，下面将进行比较分析。

3.2.1 数据集大小对CTane-IncProc性能的影响

这里使用Spawner工具生成的数据集，测试数据集的大小对CTane-IncProc性能影响。结果如图1和图2所示。从图1所得结果来看，CTane与CTane-IncProc的性能基本都与｜R｜呈指数级增长，但显然CTane-IncProc的增长率没CTane快。另外，图2显示，CTane与CTane-IncProc都与｜r｜约呈线性增长关系。

由于插入更新与删除更新都涉及CFDs_old（r）的遍历，所以，在图3中，还比较了｜CFDs_old（r）｜对3种操作（OP：INS表示插入，DEL表示删除，UPD表示更新）的影响，用到的数据集是表3中的DB1与DB2，两者在挖掘时所得的｜CFDs_old（r）｜分别为98 237、65 129。从该图可以得出：｜CFDs_old（r）｜越大，增量更新CFDs所需的时间越多，且DEL操作引起的增量计算时间比INS操作引起的增量计算时间要多。

图1 ｜R｜对性能的影响（｜r｜＝100 000，k＝10）

图2 ｜r｜对性能的影响（｜R｜＝9，k＝10）

图3 3种更新与｜CFDs_old（r）｜关系

3.2.2 CTane与CTane-IncProc的性能比较

表4列出的是CTane与CTane-IncProc作用于真实数据集中的性能对比，其中“耗时”指的是一个平均耗时，测量方法是随机增加、删除或从数据集中随机选取一条元组进行修改以作为增量元组，再利用CTane或CTane-IncProc进行挖掘，各进行30次（每次采用不同的随机元组）实验，取平均值而得。

在各次测试中，使用k＝11。从表4的实验结果可以得到如下结论：针对CTane-IncProc算法，总体上看，在3种情况下，增加元组后执行增量计算的耗时最少，更新元组后执行增量计算的耗时最多；针对非增量算法CTane，对每一数据集的挖掘时间都比更新算法的任一种情况消耗的时间多，尤其比增加元组情况下的增量挖掘时间多了近一倍。因此，实验结果证明本文提出的增量计算算法比非增量计算算法的时间效率高。

表4 CTane与CTane-IncProc的平均性能

此外，CTane-IncProc与CTane算法产生的CFDs结果相同，且通过人工判断均是正确的，表明了CTane-IncProc算法的正确性。

4 结 论

增量挖掘是分析处理海量动态数据的一项高效技术。本文首先介绍了条件函数依赖及相关概念；随后在CTane算法的基础上，分析了增、删、改3种增量操作对最小CFDs集变化的影响，并提出增量维护最小FDs集的算法CTane-IncProc，且进行了正确性和复杂度说明；最后，通过实验验证了CTane-IncProc算法的有效性。与相关研究相比，提高了CFDs的计算效率，能够为动态检测数据质量提供依据。

［1］Bohannon P，Fan W F，Geerts F，et al.Conditional functional dependencies for data cleaning［C］∥Proc.of the IEEE 23rd International Conference on Data Enginering，2007：746- 755.

［2］Huhtala Y，Karkkainen J，Porkka P，et al.TANE：an efficient algorithm for discovering functional and approximate dependencies［J］.Computer Journal，1999，42（2）：100- 111.

［3］Wyss C M，Giannella C，Robertson E L.Fast FDs：a heuristicdriven，depth-first algorithm for mining functional dependencies from relation instances-extended for abstract［C］∥Proc.of the 3rd International Conference on Data Warehousing and Knowledge Discovery，2001：101- 110.

［4］Fan W F，Geerts F，Li J Z，et al.Discovering conditional functional dependencies［J］.IEEE Trans.on Knowledge and Data Engineering，2011，23（5）：683- 698.

［5］Diallo T，Novelli N，Petit J M.Discovering（frequent）constant conditional functional dependencies［J］.International Journal of Data Mining，Modelling and Management，2012，4（3）：205- 223.

［6］Nakayama H，Hoshino A，Ito C，et al.Formalization and discovery of approximate conditional functional dependencies［C］∥Proc.of the 24th International Conference on Database and Expert Systems Applications，2013：118- 128.

［7］Beskales G，Ilyas I F，Golab L，et al.Sampling from repairs of conditional functional dependency violations［J］.The International Journal on Very Large Data Bases Journal，2014，23（1）：103- 128.

［8］Fan W F，Li J Z，Tang N，et al.Incremental detection of inconsistencies in distributed data［C］∥Proc.of the IEEE 28th International Conference on Data Engineering，2012：318- 329.

［9］Cheng L Q.Conditional functional dependency and data quality control［J］.Information System Engineering，2009，11：106-108.（程录庆.条件函数依赖与数据质量控制［J］.信息系统工程，2009，11：106- 108.）

［10］Hu Y L，Zhang W M，Luo X H，et al.Dependencies theory and its application for repairing inconsistent data［J］.Computer Science，2009，36（10）：11- 15.（胡艳丽，张维明，罗旭辉，等.基于数据依赖的数据修复研究进展［J］.计算机科学，2009，36（10）：11- 15.）

［11］Geng Y R，Liu B.Conditional functional dependencies for detecting data inconsistencies［J］.Computer Engineering and Applications，2012，48（3）：122- 125.（耿寅融，刘波.基于条件函数依赖的数据库一致性检测研究［J］.计算机工程与应用，2012，48（3）：122- 125.）

［12］Neehar C，Krishna T V S.Inconsistent relational data cleaning by detecting conditional functional dependencies［J］.International Journal of Computer Science and Information Technology&Security，2013，3（1）：120- 125.

［13］Ebaid A，Elmagarmid A，Ilyas I F，et al.NADEEF：a generalized data cleaning system［C］∥Proc.of the 39th International Conference on Very Large Data Bases，2013：1218- 1221.

［14］Bell S.Discovery and maintenance of functional dependencies by independencies［C］∥Proc.of the 1st International Conference on Knowledge Discovery and Data Mining，1995：27- 32.

［15］Han J W，Miceline K.Data mining concepts and techniques［M］.3rd ed.Fan M，Meng X F，trans.Beijing：China Machine Press，2012.（Han J W，Miceline K.数据挖掘概念与技术［M］.3版.范明，孟小峰，译.北京：机械工业出版社，2012.）

［16］Zhou J C.Research on incremental mining algorithm of conditional functional dependencies［D］.Guangzhou：Jinan University，2013.（周健昌.条件函数依赖增量挖掘算法研究［D］.广州：暨南大学，2013.）

周健昌（198-6- ），男，硕士研究生，主要研究方向为数据库、数据挖掘。

E-mail：jianchangzhou＠163.com

Incremental calculation of conditional functional dependencies

LIU Bo，ZHOU Jian-chang
（College of Information and Science Technology，Jinan University，Guangzhou 510632，China）

A conditional functional dependency（CFD）is an extension of the traditional functional dependency（FD）.By introducing the conditional pattern，the CFD is more accurate and more expressive than FDs in semantics.However，it is time-consuming for computing CFDs.In order to improve the efficiency of CFDs，the incremental maintenance method for CFDs is studied.The changing rules on the conditions of three different situations（i.e.，dataset insertion，deletion，update）are analyzed，and an incremental algorithm for calculating CFDs is proposed，so that we can efficiently and dynamically maintain CFDs while the database is changing.At the same time，the correctness of key steps of the algorithm is demonstrated，and the validness of the algorithm is verified through the experiments.

incremental calculation；conditional functional dependencies（CFDs）；data mining

TP 311.13

A

10.3969／j.issn.1001-506X.2015.11.33

刘 波（1965- ），女，教授，主要研究方向为数据库、信息集成、数据挖掘。

E-mail：ddxllb＠163.com

1001-506X（2015）11-2640-08

2014- 06- 01；

2015- 03- 22；网络优先出版日期：2015- 07- 06。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150706.1705.014.html

国家自然科学基金（U1431227）；广东省科技计划项目（2013B010401017）；广东省自然科学基金（S2012010008831）资助课题