ULA中基于LS-ICA的短时高效DOA估计
牛德智,陈长兴,陈 婷,陈 强,任晓岳,蒋 金,程蒙江川
(1.空军工程大学理学院,陕西西安710051;2.西安通信学院,陕西西安710106;3.西安邮电大学电子工程学院,陕西西安710061)
ULA中基于LS-ICA的短时高效DOA估计
牛德智1,2,陈长兴1,陈 婷3,陈 强1,任晓岳1,蒋 金1,程蒙江川1
(1.空军工程大学理学院,陕西西安710051;2.西安通信学院,陕西西安710106;3.西安邮电大学电子工程学院,陕西西安710061)
研究了均匀线阵(uniform linear array,ULA)的波达方向(direction of arrival,DOA)估计问题,提出了一种能充分利用阵列结构上来波数据的信号处理方法进行角度估计。所提方法的关键是采用天线阵列因子的实部来构造新的信号接收模型,进而通过独立分量分析(independent component analysis,ICA)对接收信号进行盲分离,用最小二乘(least square,LS)法求解入射信号的角度,同时给出了天线阵元间距应满足的条件。仿真表明,与多重信号分类(multiple signal classification,MUSIC)方法相比,本文方法能够适应阵元间距的变化,在低信噪比(signal-to-noise ratio,SNR)时估计性能以及角度分辨力均较优,通过一步粗估计就可获得较高精度且具有实时性,均方根误差(root mean square error,RMSE)向克拉美-罗界(Cramer-Rao bound,CRB)的逼近程度也说明了新方法的优势,此外还可以采用细估计来提高估计精度。
均匀线阵;波达方向;信号处理;独立分量分析;信噪比
0 引 言
基于阵列结构的信号波达方向(direction of arrival,DOA)估计在空间目标跟踪、无源定位、无线电监测、声呐传感等方面具有重要应用[12]。随着应用场合与性能要求等方面的限制和变化,传统方法往往具有某种局限性[3-4],如大多数多重信号分类(multiple signal classification,MUISC)方法需在参数空间进行搜索,计算量大,这在一定程度上制约了其时效性[5]。ESPRIT方法虽然避免了谱峰搜索,但需参数配对。为降低运算量,出现了求根MUSIC法、DOA矩阵法等[6-7],为解决相干源的DOA估计问题,改进的MUSIC法[8-9]、基于遗传算法的盲分离方法[10]等得到研究应用。
此外,文献[11]提出了基于酉变换的虚拟阵列方法,但是该方法本身要构造一个满秩的接收数据协方差矩阵的条件就较为苛刻。文献[12]提出了时空滤波压缩感知的DOA估计方法,可以实现小快拍数情况下高速目标的方位估计,但是该方法中所需的矩阵滤波器的优化问题造成了运算复杂度增加,实时性发挥受到影响。文献[13]通过分析阵列导向矢量的构成,利用等效添加镜像辐射源的思想提出了对称压缩谱的方法进行DOA估计,是对天线阵列结构的有效利用,但该方法仍然停留在MUSIC法的范围内。
本文根据前期相关研究成果[14]并考虑充分运用均匀线阵(uniform linear array,ULA)的特点,将信号处理中的独立分量分析(independent component analysis,ICA)方法与最小二乘(least square,LS)有效结合,形成LS-ICA方法进行DOA估计,目的在于为该问题研究提供一种新的解决思路。
1 信号接收模型及其基本算法
在阵元数为M的ULA中,阵元间距为d。入射信号S(t)的角度为θ,则天线系统接收信号模型如图1所示。

图1 阵列天线系统模型
假设信源的距离较远,则理想情况下阵元1上接收到的信号为x1(t)=s(t)ejω0t,其中ω0为载频,阵元2与阵元1之间的信号到达时延为τ=d sinθ/λ,则阵元2的信号[15]为

同理,阵元M上的接收信号可表示为
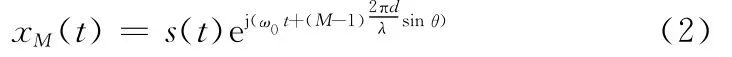
这样,输入阵列信号矢量为
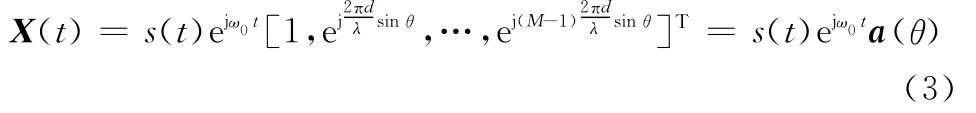
式中
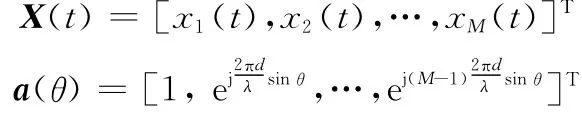
a(θ)为方向矢量。与式(3)对应的数字采样信号可表示为
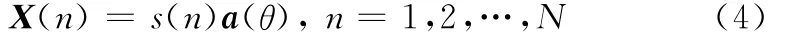
假设有L(L<M)个信号s1(n),s2(n),…,sL(n)分别以角度θ1,θ2,…,θL入射到ULA上,则接收信号的矩阵表达式为

式中,S(n)表示入射信号;A表示ULA的阵列因子矩阵。在噪声情况下,式(5)应描述为

由图1可知,波束形成器的输出为

波束形成器的总输出功率为
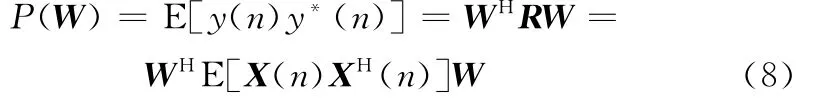
以往的DOA估计都是调节权值W使目标函数达到极值,极值点处的θ值就是波达方向,延迟-相加法、Capon最小方差法和MUSIC方法等[16]都是基于这一原理。这里给出传统 方法的空间谱表达式为

2 ICA联合LS用于DOA的可行性
在式(5)中A实质上表示了由于波程差而引起的在每个天线阵元上的相位差,由于A为一复数矩阵,所以对S(n)达到阵列后的接收信号而言,可以从实部和虚部来讨论。本文通过推导分析与验证,确定采用实部进行数据处理(原因将在后文中解释),虚部进行符号校正的方式(只采用实部会产生舷模糊问题)设计DOA估计的方法步骤。首先,取阵列因子的实数部分,得到式(5)的实数域等价表达式为

式(10)描述的只是接收信号的实部,但为便于数学表示,仍记为xi(n)。
当S(n)为复信号时,需要进行复信号的盲分离,本文仅以实信号分离为例进行说明。
令αi=2πd sinθi/λ(i=1,2,…,L),则式(10)可写为

式中,n=1,2,…,N,且需满足N>L。另外说明,本文主要考虑阵元数大于信号源个数的情形,则要求M>L。


将式(12)用矩阵表示为

求解ki的过程,就是LS问题。记每部分矩阵形式为,k,x1,式(13)可简化为

两边同乘以~S


这样就可得到式(11)中的si(n),进而αi得以求解,这就是本文方法进行DOA估计的可行性。
3 基于LS-ICA的DOA估计方法
3.1 算法流程
结合第2节中LS-ICA可行性分析,首先给出LS-ICA应用于DOA估计的算法流程,如图2所示。

图2 LS-ICA用于DOA的流程图
在图2中,DOA的粗估计和细估计是通过式(11)中方程的递进关系来实现的,这在后续将具体予以说明。
3.2 方法步骤
步骤1对ULA上的接收信号X(t)进行N点的离散采样,得M×N维大小的离散信号矩阵X(n)。
步骤2从离散信号矩阵X(n)=[x1(n),x2(n),…,xM(n)]T中任意选择L个阵列上的信号序列,得X=(n),,这里(n)为ULA中任意一个阵元上的信号序列,满足x′q(n)⊂X(n),q=1,2,…,L。接下来对L个源信号经过阵列后生成的混合信号X采用ICA方法进行盲分离处理,得到盲估计的信号序列(n),(n),…(n)。本文中选用ICA分析中常用的FastICA方法[18]进行处理。

步骤4DOA的一步粗估计过程。首先,对式(11)重新整理,得

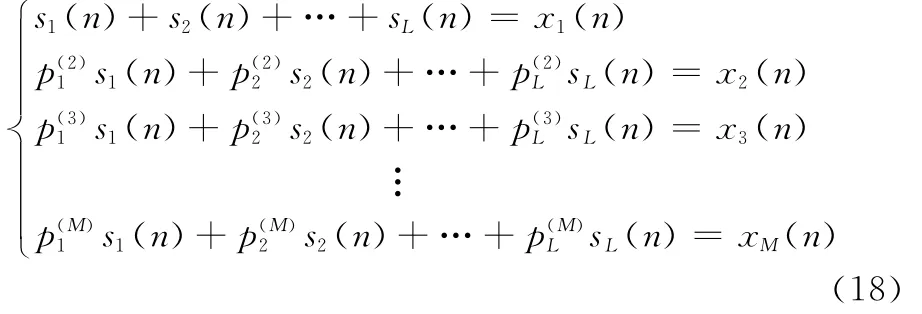
可以看出,对于αi的求解,从式(18)中的第2个方程到第M个方程,每一个或者不同行的方程相加后生成的新方程,都是典型的LS问题,这样在进行DOA估计时,就可采用M-1中的任意一个或任意几个相加所得的新等式进行求解。

式中,S和x2与式(13)的意义类似,另外S也就是式(5)中的S(n)。

进一步,联立αi=2πd sinθi/λ和p=cosαi得θi的估计值为由于arcos p∈[0,π],λ和d均大于0,故在式(20)中反正弦函数的定义区间只能满足[0,1],所以应有λ/2d≤1,即本文方法对阵元间距的要求为d≥λ/2。由∈[0,π/2]知,估计的角度值仅为半个空域。若信号方位处于正半空域,则本方法估计出的就是DOA值;若信号方位处于负半空域(-),则本方法估计出的为实际角度的绝对值。基于此,需采用阵列因子虚部产生的数据进行符号校正[14],按照式(10)~式(19)的分析过程,可得初值校正公式为

事实上,阵元间距d会对DOA估计产生影响[19],在d=λ/2时,式(20)可以简化为

通过后文不同情形下的仿真实验可以说明,粗估计所得的角度值已经具有一定精度,这就保证了方法执行的时间效率。
步骤5迭代细估计过程。从式(18)得知,每次融入更多的接收数据构造LS方程,就可以获得更高精度的角度估计值。为此,采用式(17)中每次多添加一个等式依次相加的方式产生新的LS估计问题进行求解。
首先,前3个方程相加得到
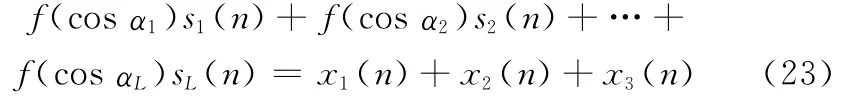
式中,f(cosαi)=1+cosαi+cos(2αi)。由于cos(2αi)=2cos2αi-1,所以
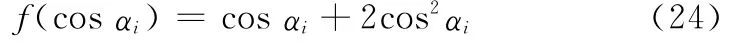

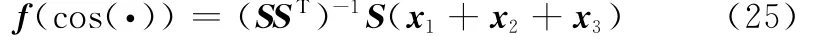
令f(cos(·))=[f(cosα1),f(cosα2),…,f(cosαL)]T,可得对于式(25)中的f(cosαi),初始值取为粗估计过程后所得的p,进而可通过“二分法”获得cosαi的数值大小,这样简化了f(cosαi)解析表达式求逆的过程,但将其结果仍记为f-1(cosαi),即用“二分法”得到cosαi=f-1(cosαi),于是得到第一次细估计过程后的估计值为

设定估计终止的条件为:本次细估计结果与上一次估计结果的差值小于给定的约束值条件时,估计停止,本次的估计结果作为最终的DOA角度值;反之不满足该条件时,重复执行下一步的细估计过程,实施过程为在式(17)中依次增加一个等式进行相加,构造出一个新LS方程,直到求解的角度值满足精度条件。
步骤6估计过程完成。
最后,将天线分集M的作用予以说明:①M可以带来角度估计精度方面的提高。这不仅可以从式(17)得到说明,而且具有物理意义,M的增大表示阵列孔径的增大,必然会带来角度估计精度的提高。②可以克服M个天线中不大于M-L个天线接收信号故障的问题,保证了复杂环境下DOA估计的可靠性。
另外指出,本节的方法过程是对于确定信源个数的情况描述的,实质上对于信号源个数未知的情况也是适用的,只是此时所要做的是首先根据盲信号处理方法确定信号源的个数,如超定情况下可采用奇异值分解方法,欠定情况下可采用非负矩阵分解、扩展子空间方法等。
4 仿真实验分析
仿真中的各参数设置如下:M=8;L=3;3个信号的时域表达式分别为s1=sin t,s2=sin(20t-0.5),s3=2.2sin(50t);入射方向分别为10°、30°和40°;信号采样率为50/π;在不专门讨论数据采样长度变化时,设定长度为1 024;噪声类型为高斯白噪声;在不考虑阵元间距变化时取d=λ/2,λ是与ω0对应的,取定ω0=2π×0.6G。此处s1、s2、s3为式(1)中s(t)的3个分量,可将其作为基带信号,而它们的载波频率相同,在载波频率不同时,d值应按照最大波长进行确定。参数设定后在Matlab软件环境中编程,进行仿真实验。
如第3节方法步骤所述,首先对ULA上的某些接收信号采用ICA方法进行盲分离处理,以期获得较为近似的原始信号。按照信号源的个数可知,应取3个天线阵元上的接收数据作为混合信号进行处理,此处选取阵元3~5的数据。确定了所选取的阵元和信号的DOA,就构成了一个对源信号线性组合的混合矩阵[11]。图3给出了ICA过程前后不同阶段的信号时域波形。

图3 ICA过程前后的不同阶段信号时域图
从ICA过程前后的各阶段信号时域图像可以看出,信号得到了较好分离,按照文中的方法求解比例系数k=[0.733 0,0.875 9,1.541 5]T。由图像排列可知信号次序有变化,但通过前文分析和后文进一步实验可知,它不会影响估计的角度值。此处对于接收信号的盲分离,在信噪比(signal-tonoise ratio,SNR)为10的情况下进行,分离后的源信号也都融入了噪声因素。对于噪声的滤除问题,可以多采集一路天线接收信号进行盲分离,在结果中将噪声单独分离出来,剩余3路信号作为纯净信号进行DOA估计,但是为了对比本文方法的抗噪性以及和MUSIC方法在同样噪声条件下进行性能比较,故此处暂时未进行滤波处理。
需要说明的是,此处的仿真实验虽然是对单频信号进行的,但是对具有一定带宽的信号盲分离也是可实现的。如同时具有单频和高斯白噪声(具有宽频特性)的信号分离效果较好(参考文献[14],这也是本文作者前期的研究结果);另外又如盲分离对于语音信号的分离适用性也比较广泛,而一般语音信号的频带范围处于300~3 400 Hz。此外,对于同频不同方向的入射信号,需要在本文方法基础上融入对相干源信号的盲分离处理过程,对相干源的处理本身就具有一定的复杂性,如文献[10]中的研究等。这种情况下本文方法的性能会受到盲分离处理结果的影响,完善相干源情况下的方法适应性也是后续研究应重点解决的问题。
4.1 阵元间距的可调节性
在本节的仿真中,令s3的入射方向为-40°,取两组阵元间距,分别为0.5λ和0.7λ,其余参数不变。对本文方法DOA估计并进行符号校正,得到结果如表1所示。同样在这两组阵元间距下,用MUSIC法进行DOA估计的结果如图4所示。

图4 MUSIC法的DOA估计曲线

表1 不同阵元间距时的DOA估计值
对比两种方法的结果可知,LS-ICA方法在两种情况下均能较好地实现DOA估计(在负方向上的角度可以根据校正方法进行符号校正,在下文的仿真中将暂时不考虑负方向的角度),MUSIC方法在阵元间距为0.5λ时可以估计出DOA,在0.7λ时出现虚假谱峰,造成实际的DOA方向难以辨认,该结论也与文献[19]是一致的。这说明,本文方法对于阵元间距的要求具有一定的调节性,该优点为天线尺寸设计带来了灵活性。实际上,对于LS-ICA法,阵元间距增大时会使得方法能估计的角度范围有所减小,但是其在满足估计一定空域的前提下,对天线尺寸所带来的可调节性优势仍然存在,关于这一点不再深入讨论。得出该结论后,在后文的仿真中将只考虑阵元间距为半波长的情况。
4.2 不同SNR下的DOA估计性能
本文方法得到的结果为角度值,用图像表示两种方法不同SNR时的DOA估计性能,如图5所示。

图5 SNR变化时的DOA估计性能
分析图像可知,MUSIC法在SNR小于0 dB时,30°和40°方向的角度信息无法辨认,LS-ICA方法在SNR较小时就能估计出3个角度值,并且其中2个角度值已经具有一定精度。分析图5(a)可知,在SNR大于6 dB时,估计结果已经收敛,由此说明了方法能够适应低SNR下的DOA估计。
为进一步比较两种方法的估计性能,首先定义角度估计的均方根误差(root mean square error,RMSE)为

引入克拉美-罗界(Cramer-Rao bound,CRB)标准进行衡量。由文献[20]可知,在ULA中,单信号源时角度估计的CRB为

事实上,本文讨论的是多源DOA估计,则应该用多源情况下的CRB分析两种方法的性能,但由双源CRB的公式[20]可知
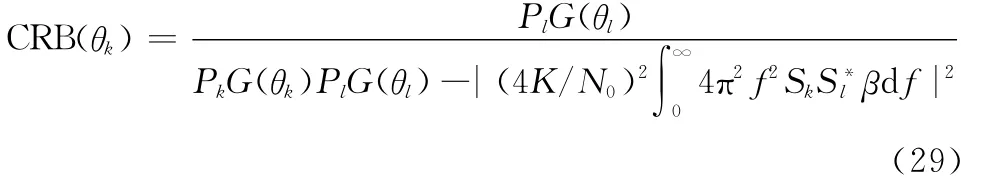
令分母中的后半部分为一正常量ε,则可将式(29)变为

分析得出,双源情况下的CRB会大于单源时的情形,类似也可得出多源时的CRB大于单源,所以为简化分析起见,用单源CRB为参考量来衡量两种方法的DOA估计性能。这样,给出两种方法估计(对30°入射信号方向的估计)的RMSE曲线及CRB,如图6所示。

图6 SNR变化时两种方法DOA估计的RMSE及其与CRB的关系
从图6可以看出,LS-ICA方法性能在低SNR时明显优于MUSIC方法,MUSIC法的RMSE曲线在低SNR时波动较大是因为该情况下不能识别出有效谱峰的个数,进而用错误的角度值作为其角度估计值的结果。当SNR增大时,两种方法的估计性能向CRB靠近。
4.3 角度分辨力
通过前面的仿真实验发现,LS-ICA法在SNR变化时DOA性能优于经典的MUSIC方法,但在SNR达一定大时,二者差别并不明显。接下来就对两种方法的角度分辨力予以讨论。
保持本节开始时的信号形式不变,并且有两路信号10°、40°的角度也不变,剩下一个的信号角度使其在35°~39°之间以1°的步进量进行变化,该情形下空间信号的来波角度较为接近,考虑此时的DOA估计角度分辨力,仿真结果如图7所示。

图7 SNR=10 d B时的角度分辨力
由图7可知,在这种情况下,LS-ICA法得出的角度值已经基本接近真实值,并且在两路入射信号角度越来越靠近时,总能估计出不重叠的3个DOA方向角,当入射信号角度间隔(dg)为1°时,本文方法仍可以辨认来波方向。在图7(b)中,MUSIC法仅能辨认到角度间隔为4°的入射信号方向,小于4°时无法辨认两个方向(谱峰由3个变为2个),此处为了观察分辨能力,10°方向估计的DOA谱峰没有绘制,特作说明。本文方法的角度分辨力约是MUSIC法的4倍(4°/1°=4倍)。
图8中给出的RMSE曲线(对信号入射方向角度不断变化并靠近另一路信号的方向角的估计)也能很好地说明这一点,当两路信号入射角度间隔小于4°时,MUSIC法的RMSE曲线迅速远离CRB,而LS-ICA方法的RMSE曲线始终保持在CRB附近的范围内,该方法具有较好的角度分辨力性能。

图8 信号入射角度间隔变化时两种方法DOA估计的RMSE及其与CRB的关系
4.4 不同数据长度对估计性能的影响
当数据长度足够长时,两种方法基本上都可以实现DOA估计,如第4.2节中的实验,但是角度间隔较大的入射信号,不易反映采样信号序列长度对不同估计性能的影响,故这里仍然采用入射角度相近的信号(10°、36°和40°)进行估计实验,图9为仿真曲线。

图9 数据长度对DOA估计性能的影响
从图9可知,在数据长度(或取样点数)为256以后的数值时(图9(a)),LS-ICA法的估计值开始向真实值收敛。而MUSIC法在数据长度为1 024时(图9(b))可以分辨出这两个相近角度。对采样数据的长度要求越高,其实时性就会下降。本文方法所需的数据长度为MUSIC法的1/4,提高了实时性。
图10所示为不同数据长度(快拍数)时两种方法的RMSE曲线(对36°入射方向角的估计)。在数据长度较小时,MUSIC方法的RMSE较大,其原因是此时没有正确估计出信源个数及角度值,LS-ICA法的RMSE较小,但会出现小范围振荡,这是因为数据长度短时估计的角度值总是在真值之间浮动。随着数据长度的增大,两种方法的RMSE均会减小,且逐渐靠近CRB,LS-ICA法的RMSE曲线总是位于MUSIC法的下方,说明了本文方法估计精度较高。

图10 快拍数变化时两种方法DOA估计的RMSE及其与CRB的关系
4.5 细估计对粗估计精度的提高
由前面的理论可知,在设定天线阵元数为8时,总共可进行7次估计过程,1次为粗估计,其余6次为细估计。图11给出了两种估计过程的精度对比图,其中横坐标序号分别对应粗估计、第1次细估计、第2次细估计、……、第6次细估计,纵坐标为估计的角度值。
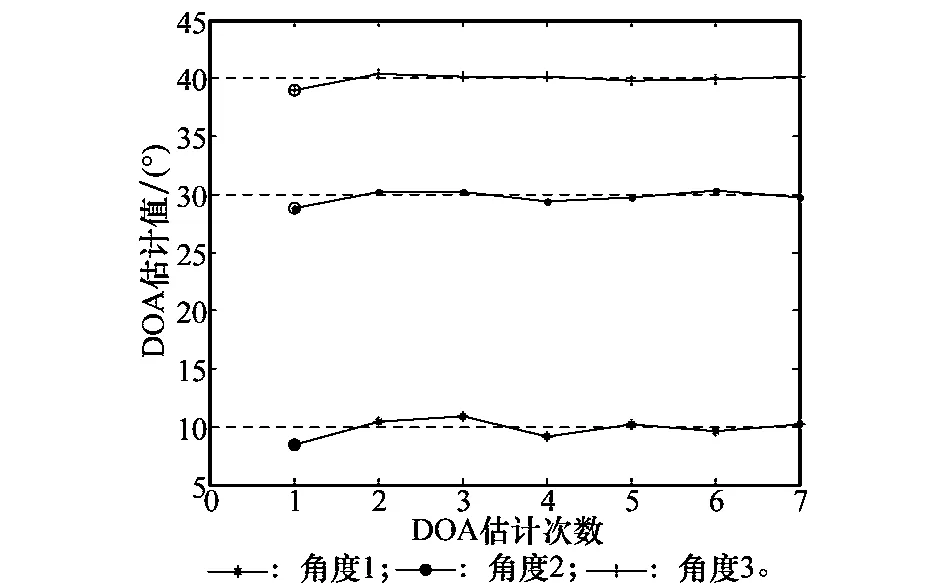
图11 6次细估计与1次粗估计的精度对比
图11表明两点:一是细估计过程进一步提高了估计精度;二是一步粗估计本身也具有了相当精度,可以满足特定场合的实时应用。
对于两种方法的计算复杂度问题,文献[14]中已做过相关的讨论及实验。本文方法在盲分离运算时采用的乘法运算,而MUSIC法中用到的矩阵特征值分解等涉及到矩阵除法运算,在大规模数量级信号处理时,会影响其时效性。所以本文方法与MUSIC法相比仍然具有计算优势,这从文献[14]中的方法执行效率曲线就可得知。
5 结 论
本文从ULA的信号处理问题入手,提出了一种新的基于LS-ICA进行DOA估计的方法,并从多个方面验证了方法的可行性。通过算法设计和仿真实验,可归纳出MUSIC方法与LS-ICA的区别与性能差异:
(1)前者通过谱图搜索极值确定DOA,后者在回归方程中直接求解入射角;
(2)前者对天线尺寸的要求较为苛刻,后者在满足估计空域的情况下使得天线尺寸可调节;
(3)前者角度分辨力不如后者,在本文参数设置下,后者的角度分辨力约为前者的4倍;
(4)前者在空间信号角度分布不均匀时(主要指信号的入射角度间隔较为接近),对数据长度的要求较高,后者较短数据便可实现(256/1024=1/4),实时性较高;
(5)后者在角度精度要求不高的场合下可以采用一步粗估计快速实现DOA估计。
另外,本文也有一些尚待完善的地方,如解决相干源估计的问题、寻找更简易方法进行符号校正的问题,这也是下一步的研究方向。
[1]Si W J,Lan X Y,Zou Y.Novel high-resolution DOA estimation using subspace projection method[J].Journal of China Universities of Posts and Telecommunications,2012,19(4):110- 116.
[2]Yan F G,Jin M,Qiao X L.Source localization based on symmetrical MUSIC and its statistical performance analysis[J].Science China:Information Sciences,2013,56(6):1- 13.
[3]Mahata K.Spectrum estimation,notch filters,and MUSIC[J].IEEE Trans.on Signal Processing,2005,53(10):3727- 3737.
[4]Zhuang X B,Cui X W,Lu M Q,et al.Low-complexity method for DQA estimation based on ESPRIT[J].Journal of Systems Engineering and Electronics,2010,21(5):729- 733.
[5]Zhang T T,Lu Y L,Hui H T.Compensation for the mutual coupling effect in uniform circular arrays for 2D DOA estimations employing the maximum likelihood technique[J].IEEE Trans. on Aerospace and Electronic Systems,2008,44(3):1215- 1221.
[6]Rubsamen M,Gershman A B.Direction-of-arrival estimation for nonunifom sensor arrays:from manifold separation to Fourier domain MUSIC methods[J].IEEE Trans.on Signal Processing,2009,57(2):588- 599.
[7]Xiong Y,Zhang G Y,Tang B,et al.Blind identification andDOA estimation for array sources in presence of scattering[J].Journal of Systems Engineering and Electronics,2011,22(3):393- 397.
[8]Luo Z,Zhang M,Li P F.A novel 2D DOA estimation algorithm based on high-order power of covariance matrix[J].Acta Aeronautica et Astronautica Sinica,2012,33(4):696- 704.(罗争,张旻,李鹏飞.基于协方差矩阵高阶幂的二维DOA估计新算法[J].航空学报,2012,33(4):696- 704.)
[9]Kundu D.Modified MUSIC algorithm for estimation DOA of signals[J].Signal Processing,1996,48(1):85- 90.
[10]Liang G L,Dong S M.Study on algorithms of blind separation and DOA estimation about coherent sources[J].Journal of Harbin Engineering University,2010,31(11):1478- 1484.(梁国龙,董姝敏.相干源盲分离及方位估计的算法研究[J].哈尔滨工程大学学报,2010,31(11):1478- 1484.)
[11]Yan J S,Peng X Y,Wang X P.A virtual array method for direction of arrival estimation based on unitary transformation[J].Journal of Harbin Institute of Technology,2012,44(4):136 -140.(闫金山,彭秀艳,王咸鹏.基于酉变换的虚拟阵列DOA估计算法[J].哈尔滨工业大学学报,2012,44(4):136- 140.)
[12]Liang G L,Ma W,Fan Z.A high resolution robust localization approach of high speed target based on vector sonar[J].Acta Physica Sinica,2013,62(14):144302.(梁国龙,马巍,范展.矢量声纳高速运动目标稳健高分辨方位估计[J].物理学报,2013,62(14):144302.)
[13]Yan F G,Liu S,Jin M,et al.Fast DOA estimation based on MUSIC symmetrical compressed spectrum[J].Systems Engineering and Electronics,2012,34(11):2198- 2202.(闫锋刚,刘帅,金铭,等.基于MUSIC对称压缩谱的快速DOA估计[J].系统工程与电子技术,2012,34(11):2198- 2202.)
[14]Niu D Z,Chen C X,Xu H X,et al.DOA estimation by independent component analysis and least square[J].Systems Engineering and Electronics,2014,36(9):1687- 1695.(牛德智,陈长兴,徐浩翔,等.独立分量分析联合最小二乘的DOA估计[J].系统工程与电子技术,2014,36(9):1687- 1695.)
[15]Palanisamy P,Kalyanasundaram N,Raghunandan A.A new DOA estimation algorithm for wideband signals in the presence of unknown spatially correlated noise[J].Signal Processing,2009,89(10):1921- 1931.
[16]Shan Z,Yum T.A conjugate augmented approach to direction of arrival estimation[J].IEEE Trans.on Signal Processing,2005,53(11):67- 94.
[17]Bobin J,Starck J L,Moudden Y,et al.Blind source separation:the sparsity revolution[J].Advances in Imaging and E-lectron Physics,2008,152(1):221- 302.
[18]Niu D Z,Chen C X,Wang S Z,et al.Research on channel estimation of MIMO system based on FastICA[J].Computer Engineering and Applications,2012,3(5):152- 156.(牛德智,陈长兴,王曙钊,等.FastICA在MIMO信道估计中的应用研究[J].计算机工程与应用,2012,3(5):152- 156.)
[19]Guo Y,Wang H Y,Zhou Z.Effect of array elements spacing on MUSIC algorithm[J].Acta Electronica Sinica,2007,35(9):1675- 1679.(郭跃,王宏远,周陬.阵元间距对MUSIC算法的影响[J].电子学报,2007,35(9):1675- 1679.)
[20]Liu J G,Yuan B C,Yan S G,et al.The CRB of direction estimation for underwater wide band sources[J].Acta Acustica,2010,35(5):539- 546.(刘建国,苑秉成,严胜刚,等.水下宽带源方位估计的克拉美-罗界研究[J].声学学报,2010,35(5):539- 546.)
牛德智(198-4 -),男,讲师,博士,主要研究方向为通信系统与雷达信息处理。
E-mail:niudezhi_001@163.com
陈长兴(1964 -),男,教授,博士,主要研究方向为现代通信理论、信息系统建模与仿真。
E-mail:xachenchangxing@126.com
陈 婷(199-2 -),女,硕士研究生,主要研究方向为信息系统建模仿真。
E-mail:chen-ting2014@163.com
陈 强(198-9- ),男,硕士研究生,主要研究方向为信号与信息处理。
E-mail:chenqiang2013@163.com
任晓岳(198-9 -),男,博士研究生,主要研究方向为信号与信息处理。
E-mail:776596484@qq.com
蒋 金(199-0- ),男,硕士研究生,主要研究方向为电路理论与应用。
E-mail:jin-jiang2013@163.com
程蒙江川(1990- ),男,硕士研究生,主要研究方向为信息处理。
E-mail:CMjiangchuan2013@163.com
Quick DOA estimation with high efficiency based on LS-ICA in ULA
NIU De-zhi1,2,CHEN Chang-xing1,CHEN Ting3,CHEN Qiang1,REN Xiao-yue1,JIANG Jin1,CHENGMENG Jiang-chuan1
(1.College of Science,Air Force Engineering University,Xi’an 710051,China;2.Xi’an Communications Institute,Xi’an 710106,China;3.School of Electronic Engineering,Xi’an University of Posts&Telecommunications,Xi’an 710061,China)
The problem of direction of arrival(DOA)estimation based on uniform linear array(ULA)is studied.A signal processing method by making full use of the receiving data in the antenna array is proposed to estimate angles of spatial signals.The key point is to construct a new model of received signals by adopting the real part of the antenna array cell,next to implement blind source separation for received signals by independent component analysis(ICA),and solve incident angles by the least square(LS)method.The requirement for antenna array cell internal is given in the process of the algorithm.Simulation experiments show that compared with the multiple signal classification(MUSIC)method,the new method is more suitable for adjusting the antenna array cell internal,has better estimation performance in low signal-to-noise ratio(SNR)and degree distinguishing capacity,and achieves high precision by one-step crude estimation and good real time performance.Also,its merit is illustrated by the root mean square error(RMSE)curve and Cramer-Rao bound(CRB)characteristics.Furthermore,estimation precision can be improved by refined estimation course.
uniform linear array;direction of arrival(DOA);signal processing;independent component analysis(ICA);signal-to-noise ratio(SNR)
TN 911.7;TN 957.52
A
10.3969/j.issn.1001-506X.2015.11.03
1001-506X(2015)11-2438-09
2014- 09- 12;
2015- 03- 03;网络优先出版日期:2015- 04- 16。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150416.0932.002.html
陕西省自然科学基础研究计划项目(2014JM8344)资助课题

