基于OI-AGCD的含旋转部件目标ISAR成像
吕贵洲,罗贤全
(军械工程学院电子与光学工程系,河北石家庄050003)
基于OI-AGCD的含旋转部件目标ISAR成像
吕贵洲,罗贤全
(军械工程学院电子与光学工程系,河北石家庄050003)
旋转部件(如直升机的螺旋桨)严重影响逆合成孔径雷达(inverse synthetic aperture radar,ISAR)的成像特性,基于优化初值选择的自适应高斯包络线性调频基分解(optimized initial-adaptive Gaussian chirplet decomposition,OI-AGCD)设计了一种自适应旋转部件回波分离算法。建立了含旋转部件目标步进频率雷达ISAR成像模型,分析了旋转部件与目标主体回波特性差别。基于距离-- 多普勒成像理论、主体和旋转部件回波在高斯基上投影的差异,设计了基于OI-AGCD的旋转部件回波分离算法。仿真数据验证结果表明了该算法去除旋转部件回波的可行性,含旋转部件类目标ISAR成像质量得到了有效提高。
逆合成孔径雷达;自适应分解;时频分析;直升机
0 引 言
逆合成孔径雷达(inverse synthetic aperture radar,ISAR)通常用于固定平台对非合作目标进行成像,如舰船、飞机、空间星体等。ISAR成像高的距离分辨力利用发射宽带信号获得,高的方位分辨率利用较大的角度观测获得。ISAR成像方法分为傅里叶变换法、现代信号谱估计法和非平稳信号处理方法[12]。无论采用何种方法,对目标的要求是小观测角范围内散射点的位置、强度和特性不变,即目标必须是钢体[3]。然而,非钢体运动情况很多,如带有螺旋桨的直升飞机、带有扫描天线的舰船等都包含旋转部件。对于这些情况,钢体假设不再成立,旋转部件回波会给目标成像带来负面影响,因此对旋转部件回波的处理(识别、分离)是得到清晰像的必备步骤。____
针对带有旋转部件目标的雷达成像,文献[4]研究了旋转部件目标的包络对齐问题,提出了通过一组回波形成稳定的参考回波、弱化回波中螺旋桨子回波的影响,实现包络对齐;由于旋转部件的存在,目标回波具有明显的非平稳特征,时频分析方法被广泛应用到子回波分离中。文献[5]采用Wigner-Ville分解(Wigner Ville decomposition,WVD)分析了直升机回波信号的调制特性,对单个旋转点模型数据取得较好结果,但当同时存在多个旋转点时,WVD的交叉项问题难以解决。
为解决WVD等二次型时频分析算法交叉项问题,自适应分解方法被应用到ISAR成像中。文献[6]将自适应高斯基分解(adaptive Gaussian basis representaion,AGR)算法[7]应用到散射和非散射效应的分离中,消除了非散射点在图像中造成的模糊现象。
AGR算法采用的高斯基函数不含调频项,对包含调频信息的信号缺乏有效的处理能力。针对该问题,文献[8]将调频项引入到高斯基函数中,形成了高斯包络线性调频基分解。
文献[12,14]提出自适应高斯包络线性调频基分解(adaptive Gaussian chirplet decomposition,AGCD)算法,利用最优化方法解决多维参数的搜索问题,通过构造和求解超越方程实现多维优化搜索,得到基元Chirplet各参数解析解,在保证分解精度的同时,运算量明显降低,自适应分解的实用性进一步增强。时频分辨率上AGCD算法表现出色,在可由调频类信号建模的信号分析中分辨能力超强[12]。
对于在时频平面上基函数深相交的复杂信号,AGCD由于初值选择问题使得分解结果不合实际,文献[13]提出了基于优化初值选择的AGCD算法,对初值进行优化,提高了精度,同时降低了运算量。
现有的旋转部件回波分离算法[910]主要针对单个旋转点进行处理,在现实情况下采用单个旋转点对如桨叶,尤其是多个叶片的螺旋桨进行建模显然是不合实际的。由于多个旋转点的回波非平稳特征更加复杂,处理这种复杂信号AGCD算法效果较差。本文将基于优化初值选择的自适应高斯包络线性调频基分解(optimized initial-adaptive Gaussian chirplet decomposition,OIAGCD)算法应用到多旋转点回波分离中,实现了多旋转点回波信号分离,大大提高了带有旋转部件的复杂目标的成像质量。
1 OI-AGCD原理及性能
针对自适应分解中的运算量问题,文献[12]采用解四维变量方程组的方法获得分解参量,极大地降低了运算量。但是分解过程中的初值选择对结果影响重大,对深相交复杂信号AGCD能量峰值策略并不适用,文献[13]提出的OI-AGCD算法对其初值选择方法进行了补充,提高了AGCD处理复杂深相交信号的能力。
AGCD及OI-AGCD算法采用的基函数为复高斯包络线性调频信号

式中,tk为基函数的时间中心;ωk为基函数的频率中心;信号宽度由αk决定;βk表示调频斜率。OI-AGCD相对于AGCD具有更优性能,采样率1 MHz,分析信号

式中

该信号表示同一距离单元两个对称旋转点的多普勒频移特征,图1表示不同时频分解算法的分析结果。

图1 复杂机动信号不同时频分析方法分辨性能
从图1可以看出,OI-AGCD对复杂变化规律多普勒信息提取具有更高的分辨力。WVD交叉项明显,而AGCD对复杂信号不具备适应性。
2 旋转部件回波特征分析
2.1 信号模型
在雷达成像中通常采用散射点模型对未知目标进行散射模型的建模。将目标回波表示为一系列散射点回波的叠加,用M个独立散射点对未知目标进行建模,则其回波表达式为

式中,信号E是频率f和时间t的函数;σm为第m个散射点的复散射系数;Rm(t)为散射点的瞬时距离;f为载波频率。假设目标的运动包含平动(t)和转动θm(t),(xm,ym)表示散射点的位置,根据雷达成像中通常采纳的目标为钢体的假定[10]可以得到
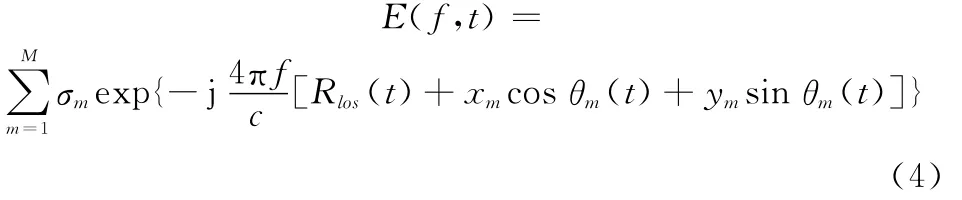
为便于分析带有旋转部件的复杂目标回波,将目标本身和旋转部件分别假定为钢体,并假定旋转部件上的独立散射点个数为N,得到如下的回波[10]表达式
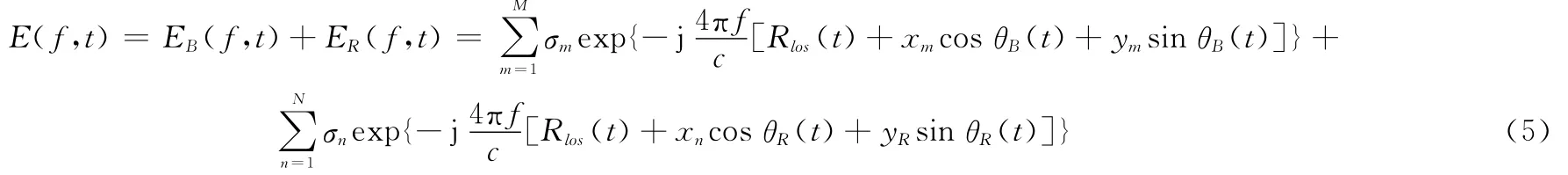
式中,下标B和R分别表示目标主体和旋转部分。显然旋转部分和目标主体共享同一平动分量,对于主体部分,在雷达成像期间通常满足小角度假设,即

假设进行成像处理之前对目标回波进行了标准的运动补偿,补偿后的信号仅仅包含标准的旋转运动,即

这里用0代替目标的平动分量,ωB为目标的归一化旋转角速度,而旋转部分的旋转角仍然用θR(t)表示,这是因为旋转部件的运动不再满足小角度假设。将式(6)、式(7)代入式(5),得到
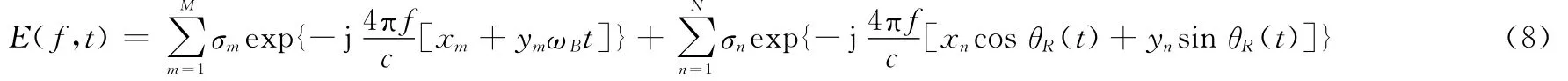
2.2 步进频率雷达旋转部件回波仿真及分析
对步进频率雷达旋转部件回波进行仿真,参数和目标模型如表1和图2所示。

表1 步进频率雷达参数_

图2 旋转部件独立散射点模型
由表1的雷达参数可以得到雷达的最远作用距离为1.5 km,最大非模糊距离窗为150 m,径向距离分辨力为0.59 m。图2中的4个旋转部件上的旋转点(a,b,c,d)围绕旋转中心o作逆时针旋转,旋转角速度为6πrad/s。
考察图2中旋转点b、d的影响,这类似于偶数螺旋桨直升机上对称桨叶的回波数据。以第1和第64个脉冲串的数据为例,第1个脉冲串形成的径向距离像,第64个脉冲串发射时刻的横向距离像、a,o,c 3点对应距离单元的时频分布,完整二维像如图3所示。
从图3(b)可以看出,由于旋转部件的高速旋转使得横向距离像展宽到若干个距离单元,正是由于这种横向距离像的展宽使得旋转部件形成的二维像扩展到椭圆状区域,如图3(d)所示。图3(c)显示的是两个对称旋转点回波的多普勒信息的变化规律,其调制特征非常明显。多个旋转点的存在使得目标的回波数据更加复杂,时频平面上这种回波由多个正弦或余弦规律变化的多普勒时变曲线相互交叉,其信号回波的时变性更强。采用AGCD和OI-AGCD进行100条高斯基分解,得到的时频分布如图4所示。

图3 两个对称旋转点回波分析

图4 对称旋转点回波的AGCD及OI-AGCD时频分布
对比图4(a)和图4(b),OI-AGCD的分解效果明显强于AGCD,旋转部件回波的高斯基参数具有如下特征:
(1)在多普勒信息变化斜率较大的阶段,得到的高斯基的调频斜率β较大,如图3(c)中由A点到B点之间的变化曲线;
(2)多普勒信息变化的转折点处,高斯基的中心频率的模较大,如图3(c)中A点和B点附近;
(3)旋转部件回波的高斯基长度αk较小。
文献[9- 10]以上述(1)(2)两个特征设定准则对旋转部件回波信号进行分离,本文加入高斯基长度判断,进一步去除旋转部件弱回波信号。
3 OI-AGCD旋转部件回波分离
3.1 旋转部件回波分离的必要性
旋转部件回波对目标像形成干扰,造成目标像模糊,给目标成像和识别带来巨大困难。抑制或消除旋转部件回波是处理带有旋转部件目标回波信号的重要手段,现有的算法对处理旋转部件采用了单个旋转点的假设,虽然取得了较好的效果,但是在实际应用中单旋转点的假设过于简单。为此,针对多个旋转点情况提出基于OI-AGCD的旋转部件回波分离算法。
3.2 分离算法
根据OI-AGCD算法对旋转部件回波分解得到的高斯基参数的特征,旋转部件回波分离的ISAR成像算法如下:
步骤1将回波数据按距离单元存储构成二维矩阵S,行为每一个发射脉冲按距离单元存储的回波,列为同一距离单元不同发射脉冲的回波;
步骤2对S的每一列信号作能量剩余小于1%(作为结束条件)的高斯基自适应分解,记分解次数为K,调频斜率最大值为βmax=MAX(βi),i=1,2,…,K,则旋转部件和主体部分与βmax所在的距离单元相同;
步骤3对D中包含旋转部件距离单元(设其为第i个距离单元)回波的信号作K个高斯基自适应分解,分解参数集合P={Pk,1≤k≤K},其中Pk=(Ak,αk,tk,ωk,βk);


从分解参数数组P中去除基函数,得到新分解参数集
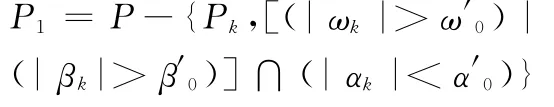
式中,α′0,ω′0和分别对应高斯基信号的长度,中心频率和调频斜率的门限值;


步骤7对D1应用传统的距离多普勒成像算法,得到目标二维像。
3.3 仿真分析
仿真中目标本身及旋转部件的几何结构如图5所示。这里用9个“×”型散射点表示目标本身,用2个“●”型散射点表示旋转部件。仿真中采用的雷达参数如表1所示,目标本身的旋转角速度为0.02 rad/s,旋转部件围绕旋转中心(散射点5)以5πrad/s的角速度转动。
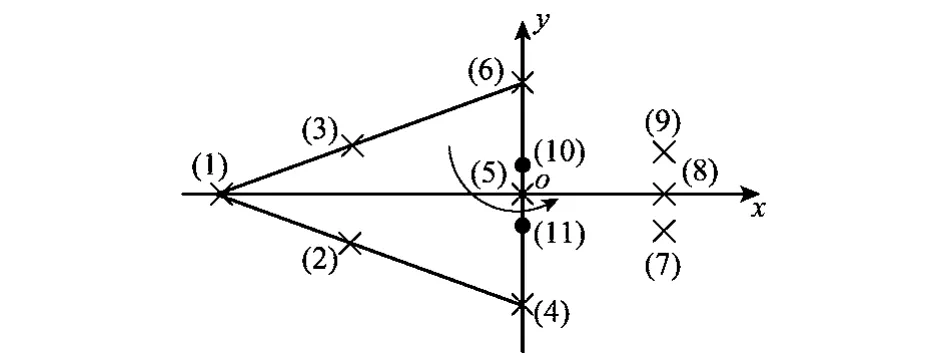
图5 含旋转部件的仿真目标模型
采用传统距离 多普勒方法得到的二维像及第170个距离单元(对应旋转中心)信号的时频分布分别如图6所示。

图6 两个对称旋转点的回波分析
从图6(a)可以看出:中间距离单元3个独立散射点被两个旋转点形成的多普勒噪声所覆盖,这极大地影响了目标成像质量,给目标识别和成像带来了负面影响。采用OI-AGCD旋转部件回波分离算法,对第170个距离单元目标本身和旋转部件的回波数据进行100个高斯基自适应分解,得到时频分布如图7所示。

图7 目标散射点和旋转部件回波OI-AGCD谱
主目标(对应于图5中的4,5,6散射点)和旋转部件回波时频分布特征差别,正是基于这种差别提出旋转部件回波分离算法。第170个距离单元的复合目标回波信号的时频分布如图8(a)所示,高斯基中心频率门限值ω0=1.5 rad/s,调频斜率β0=0.005 rad/s2,得到第170个距离单元分离出旋转部件回波后剩余信号时频分布,如图8(b)所示,去除所有距离单元回波信号中旋转点子回波,目标二维像如图8(c)所示。

图8 第170距离单元复合目标分离后的时频分布及重构二维像
比较图2(a)和图8(b)可以看出,经过OI-AGCD分离算法得到的剩余回波和目标本身的4、5、6 3个独立散射点的回波非常接近,证明OI-AGCD算法分离多旋转点回波数据是有效的。对比图6(a)和图8(c),将旋转部件回波信号分离后,目标本身成像质量得到有效提高。
4 结 论
成像目标包含旋转部件时,相互干扰的旋转部件和目标本身回波极大地影响成像质量和目标识别效果。AGCD在提取旋转部件回波时只能对单个旋转点进行处理,而实际情况采用一个旋转点近似旋转部件是不够的。为了解决多旋转点的回波分离问题,本文首先给出了带有旋转部件的目标回波模型,优化了旋转部件回波分离准则,提出了基于OI-AGCD的旋转部件回波分离算法。多个仿真实例表明该算法在多旋转点回波信号分离中的有效性,通过回波分离,目标钢体部分散射点的聚焦性能得到了提高,得到了高质量的ISAR像。
[1]Wehner D R.High resolution radar[M].London:Artech House Publishers,1987.
[2]Walker J L.Range-Doppler imaging of rotating objects[J].IEEE Trans.on Aerospace and Electronic Systems,1980,16(1):23- 52.
[3]LüX G,Hao S Q,Leng J F,et al.Synthetic aperture radar imaging based on time frequency analysis[J].Electronic and Information Warfare Technology,2012,27(5):22- 26.(吕旭光,郝士琦,冷蛟锋,等.基于时频分析的合成孔径激光雷达成像算法[J].电子与信息对抗技术,2012,27(5):22- 26.)
[4]Lu G Y,Bao Z.Range alignment for targets with moving parts in ISAR imaging[J].Systems Engineering and Electronics,2000,22(6):12- 14.(卢光跃,保铮.ISAR成像中具有游动部件目标的包络对齐[J].系统工程与电子技术,2000,22(6):12- 14.)
[5]LüJJ,Ding J J.Analysis on signal characters modulated by rotating structures of helicopter for air defense radar based on WVD[J].Radar and Countermeasure,2004,10(4):37- 39.(吕金建,丁建江.基于WVD的防空雷达直升机信号特征分析[J].雷达与对抗,2004,10(4):37- 39.)
[6]Sun Z Z,Chen Z P,Zhuang Z W,et al.A method of understanding and processing ISAR image based on time-frequency analysis[J].Journal of Electronics&Information Technology,2003,25(1):1- 8.(孙真真,陈曾平,庄钊文,等.一种基于时频分解的ISAR图像理解与处理方法[J].电子与信息学报,2003,25(1):1- 8.)
[7]Qian S,Chen D.Signal representation using adaptive normalized Gaussian functions[J].Signal Processing,1994,36(6):1- 11.
[8]Qian S,Chen D,Qinye Y.Adaptive chirplet based signal approximation[C]∥Proc.of the IEEE International Conference on Acoustics,Speech and Signal Processing,1998,1781- 1784.
[9]Li J F,Ling H.ISAR Feature extraction from targets with nonrigid body motion using adaptive chirplet representation[C]∥Proc.of the IEEE Antennas and Propagation Society International Symposium,2002:294- 297.
[10]Li J,Ling H.Application of adaptive chirplet repre-sentation for ISAR features extraction from targets with rotating parts[J].Radar,Sonar Navigation,2003,150(4):284- 291.
[11]Stephane G,Mallat H.Matching pursuits with time-frequency dictionaries[J].IEEE Trans.on Signal Processing,1993,41(12):3397- 3415.
[12]Yin Q Y,Qian S,Feng A G.A fast refinement for adaptive Gaussian chirplet decomposition[J].IEEE Trans.on Signal Processing,2002,50(6):1298- 1306.
[13]LüG Z,He Q Wei Z S.Optimized initial-adaptive Gaussian chirplet signal decomposition[J].Signal Processing,2006,22(4):506- 510.(吕贵洲,何强,魏震生.基于优化初值选择的自适应高斯包络线性调频基信号分解[J].信号处理,2006,22(4):506- 510.)
[14]Feng A G,Yin Q Y,LüL.An adaptive fast algorithm for decomposition of signal based on Gaussian chirplet[J].Progress in Natural Science,2002,12(9):982- 988.(冯爱刚,殷勤业,吕利.基于Gauss包络Chirplet自适应信号分解的快速算法[J].自然科学进展,2002,12(9):982- 988.)
[15]Hagelen M T.ISAR-imaging of helicopters at millimeter-wave frequencies[J].Euro Radar Proceeding,2004,16(1),67- 70.
吕贵洲(197-7- ),男,讲师,博士,主要研究方向为电子装备测试与故障诊断、非平稳信号处理、雷达信号处理及雷达成像。
E-mail:lgz2691@163.com
罗贤全(1977- ),男,讲师,博士,主要研究方向为信号处理、电子装备测试与故障诊断。
E-mail:luoweed@163.com
ISAR imaging of targets with rotating parts based on OI-AGCD
LÜGui-zhou,LUO Xian-quan
(Electronic and Optical Department,Ordnance Engineering College,Shijiazhuang 050003,China)
Echoes produced by rotating parts,such as propellers of helicopters,seriously worsen inverse synthesizer aperture radar(ISAR)imaging quality.An algorithm based on optimized initial adaptive Gaussian chirplet decomposition(OI-AGCD)is proposed.Firstly,the ISAR imaging model which involves the target with rotating parts,based on stepped frequency radar,is established.The different performances between the main body and the rotating parts are analized.Secondly,based on range-Doppler imaging theroy and the different projection properties of main body and roating parts on Gaussian bases,the algorithm of cleaning rotating parts’radar echoes based on AGCD is proposed.Finally,simulation results show the effectiveness of the algorithm to eliminate echoes produced by rotating parts and high quality images can be achieved.
inverse synthesizer aperture radar(ISAR);adaptive decomposition;time-frequency analysis;helicopter
TN 911.7
A
10.3969/j.issn.1001-506X.2015.11.11
1001-506X(2015)11-2492-05
2014- 04- 22;
2015- 05- 28;网络优先出版日期:2015- 07- 07。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150707.1451.008.html
国家自然科学基金(61372039)资助课题

