MIMO-ISAR成像空时等效误差校正方法

董会旭，张永顺，冯存前，胡晓伟

（空军工程大学防空反导学院，陕西西安710051）

MIMO-ISAR成像空时等效误差校正方法

董会旭，张永顺，冯存前，胡晓伟

（空军工程大学防空反导学院，陕西西安710051）

针对多输入多输出逆合成孔径雷达（multiple-input multiple-output inverse synthetic aperture radar，MIMO-ISAR）成像中的空时不等效问题，首先建立了空时等效误差模型，并对模型进行了分析，然后推导出空时等效误差的校正模型，得出了空时等效误差的校正矩阵，且该误差校正矩阵只与空时等效失配率有关。采用特显点方位像熵最小对空时等效失配率进行了估计，并利用它构建出空时等效误差的校正矩阵，实现了MIMO-ISAR空时等效误差的校正。仿真验证了这一方法的有效性。

多输入多输出逆合成孔径雷达成像；空时等效失配率；空时等效误差校正

0 引 言

多输入多输出逆合成孔径雷达（multiple-input multiple-output inverse synthetic aperture radar，MIMO-ISAR）成像是新近提出的一种成像方法。它既可以借助多输入多输出（multiple-input multiple-output，MIMO）雷达虚拟等效阵列提高其空间采样的能力，减小成像积累时间，以降低非合作目标运动对成像的影响；又可以利用雷达与目标的相对运动弥补MIMO虚拟阵元的空间欠采样。因而，MIMOISAR成像技术迅速成为国内外学者研究的焦点［18］。

由于MIMO-ISAR成像具备诸多优点，国内外学者针对该成像技术进行了研究：文献［9］首先通过数据重排将多通道数据联合处理，然后利用插值对成像数据进行均匀化处理，最后使用距离-多普勒（range-Doppler，R-D）算法进行成像，对MIMO-ISAR成像技术进行了验证；文献［10］利用相位中心近似（phase center approximation，PCA）原理，将其提出的MIMO阵列等效为收发一体的均匀面阵，并利用空时信号联合处理的方法对目标进行MIMO-ISAR三维成像；文献［11］基于面阵建立了MIMO雷达成像信号模型，分析了在MIMO雷达成像中阵列结构设计、特显点选择准则以及正交波形发射策略等，并实现了MIMO雷达对运动目标的单次快拍成像；文献［12］讨论了MIMO雷达对运动目标的多快拍成像，对成像所需的图像校正方法及目标速度估计进行了分析，提出了利用MIMO-ISAR技术对运动目标三维成像；文献［13］采用MIMO技术的侧视ISAR对微转动目标进行成像，增强了成像的方位分辨率。

在MIMO-ISAR成像过程中，由于目标的非合作性，使得MIMO雷达空间采样与时间积累不能有效等价（即空时不等效），会造成回波数据空间非均匀。文献［14］针对空时不等效对成像的影响进行了定量分析，得出在空时等效失配情况下虚假目标的位置、数量及真假目标间幅度的定量关系式，为空时等效误差校正提供了有益借鉴。但是，对MIMO-ISAR成像空时等效误差的校正方法研究则很少涉及。

针对MIMO-ISAR成像中的空时不等效问题，本文首先建立空时等效误差模型，并对其进行分析，根据频域重构思想推导出空时等效误差的校正模型；然后利用方位像熵最小的方法估计空时等效失配率，构建等效误差校正矩阵，实现对空时等效误差的校正；最后利用Matlab数值仿真验证了这一方法的有效性。

1 空时等效误差建模与分析

不失一般性，建立MIMO-ISAR成像几何模型，发射、接收阵元分布于X轴上，阵列参数设置为：发射、接收阵元数分别为M和N，其中，发射阵元间距为dt，接收阵元间距为dr，发射阵列与接收阵列间隔为dtr，且满足dt＝Ndr，如图1所示。由等效相位中心近似（phase center approximation，PCA）定理，该阵列结构可等效为MN个收发共用阵元组成的均匀线阵［2］。若积累时间内的发射脉冲数为P，则整个系统积累了MN×P个脉冲。

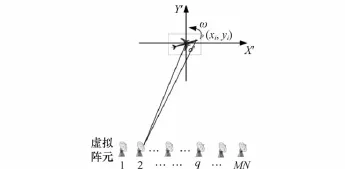
图1 MIMO-ISAR成像几何模型

采用传统ISAR成像方法，利用文献［2］平动补偿方法，将目标运动转化成转台模型，如图1所示。由于MIMOISAR成像可以大幅减小积累时间，目标转动可近似为匀速［2］，那么目标上第i个散射点（xi，yi）相对于第q（q＝1，2，…，MNP）个阵元的距离变化为

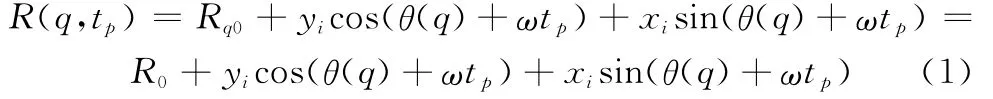
式中，θ（q，tp）为散射点在tp时刻相对于第q个阵元的转台夹角；ω为转速；Rq0为第q个阵元到目标中心的距离，在平动补偿完成时所有阵元到目标中心的距离都相同，记为R0。由于时间积累过程中的转角很小，可近似cos（θ（q）＋ω tp）≈1，sin（θ（q）＋ωtp）≈θ（q）＋ωtp，那么，式（1）近似为

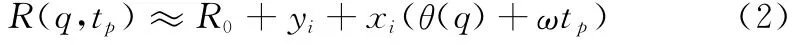
式中，θ（q）表示空间阵元采样引起的转角变化；ωtp表示目标运动引起的转角变化。为方便分析，此处暂不考虑距离徙动的影响，则MIMO-ISAR回波信号模型为

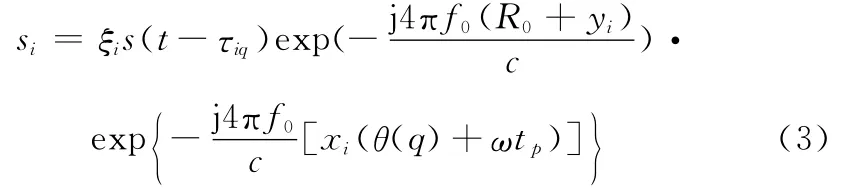
式中，ξi为第i个散射点的散射系数，为便于分析，不妨设ξi＝1；s（t－τiq）为第i散射点的一维距离像包络。由于MIMO虚拟阵列为均匀阵列，因而有θ（q）＝（q－1）Δθ，若MIMO阵列虚拟等效阵元间隔为d0，Δθ≈d0／R0。理想情况下，对回波进行空时等效并做均匀化处理，则式（3）转化为

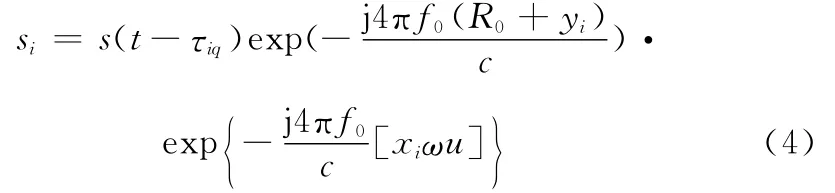
式中，u＝（iu－1）Tq／P，iu＝1，2，…，P。

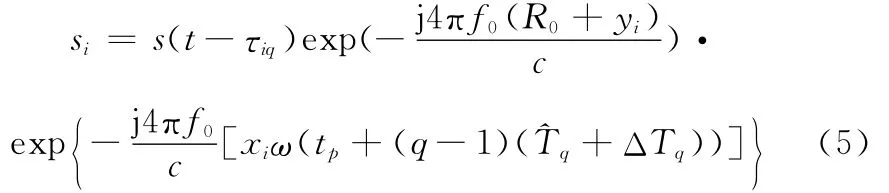
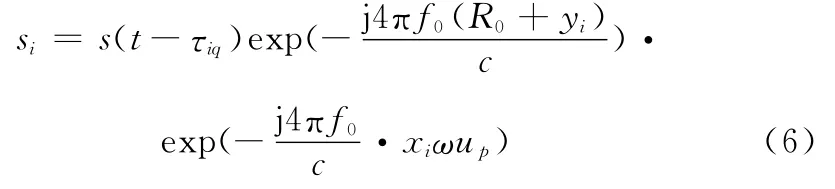
式中

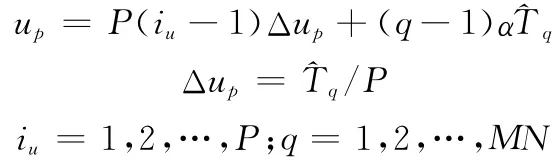
α为失配率［14］，α＝ΔTq／Tq，0≤α＜1。此时，回波数据在横向为周期非均匀采样。

依据up构建回波数据的离散傅里叶变换矩阵

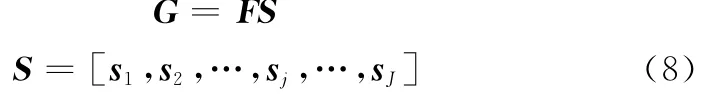
式中，sj表示第j个距离单元的回波数据组成的列向量。由于目标匀速转动，那么在空时等效误差不存在时，式（10）离散傅里叶变换所得G即为目标的二维像，文中称为校正像，记为G0；在等效误差存在时，由于傅里叶变换阵失配，G会出现虚假目标，造成成像质量下降，文中称为误差像，记为Ge。

由文献［15］中周期非均匀采样序列的频谱与均匀采样序列的频谱之间的关系，可得单个距离单元的误差像与校正像存在如下关系：

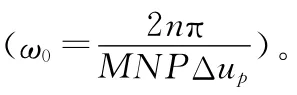
式中

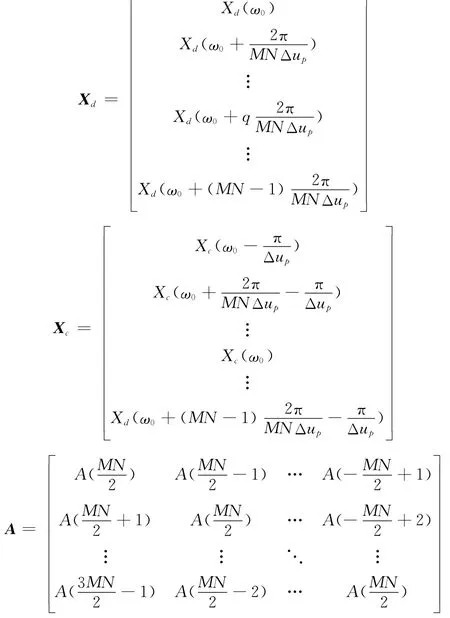
综合式（8）～式（10），可得

即

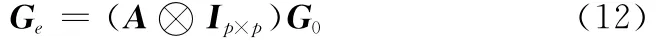
式中，⊗表示kronecker积。令H＝A⊗Ip×p，误差像等于校正像左乘矩阵H，H只与失配率α有关，记H为空时等效误差矩阵，只需估计出失配率α，就可以通过式（12）对空时等效误差进行校正。

2 误差校正方法

通过第1节分析，得出了误差像与校正像之间的关系式。由式（11）、式（12）可知，

式中，H†表示H的广义逆。利用式（13）就可以实现空时等效误差的校正。综合上述分析，能否利用式（13）对空时等效误差进行校正取决于两个关键问题：一是H†求解计算量的问题；二是空时等效失配率α是否已知。

因为H＝A⊗Ip×p，Ip×p为单位阵，考察矩阵A可知，A为Toeplitz矩阵，它的广义逆求解有快速算法，计算量为o（M2）。那么矩阵H＝H†⊗Ip×p，称H†为误差校正阵。

由式（11）、式（13），可得

由于矩阵H、F只与等效失配率α有关，S为回波信号，因此

对校正像G0求图像熵

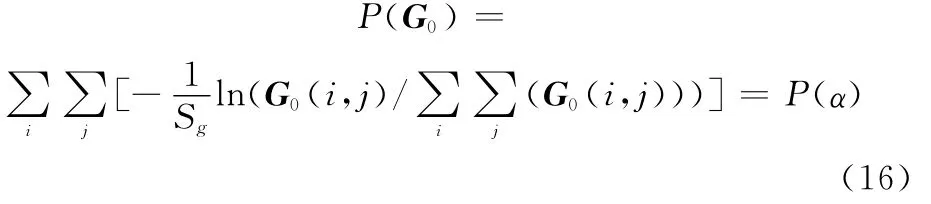
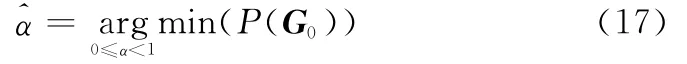
由于求解式（17）需要对α全局搜索，且反复求熵，计算量较大，为减小运算量，可以选取特显点回波g0，求方位像最小熵所对应的α，即

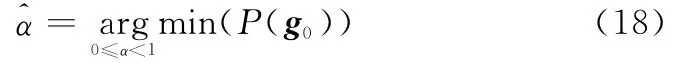
3 仿 真

仿真参数设置：仿真采用3发4收MIMO阵列，发射阵元坐标（单位：m）为（－300，0，0），（－180，0，0），（－60，0，0），接收阵元坐标（单位：m）为（60，0，0），（90，0，0），（120，0，0），（150，0，0）。目标做匀速直线运动，目标阵列方向的运动速度估计误差为7 m／s，即空时等效失配率为0.046 7；目标散射点位置如图2所示。从目标中心到阵列中心的斜距R0设为10 000 m，搜索步长μ＝0.001。

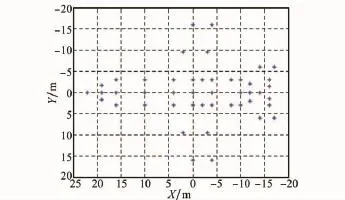
图2 目标散射点位置图

设置雷达参数如表1所示。

表1 雷达参数

仿真结果如图3和图4所示。

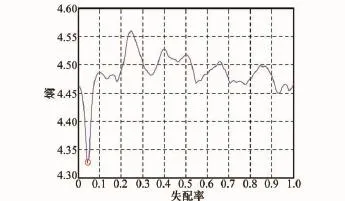
图3 特显点方位像最小熵估计失配率估计

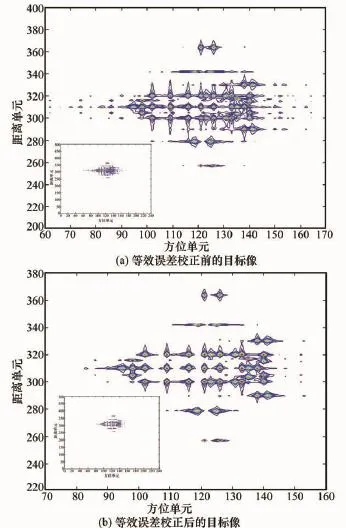
图4 空时等效误差校正前后目标像对比

图3为特显点方位像的熵随空时等效失配率α的变化曲线，最小熵为4.328，熵最小时（图中红圈所示）所对应的α即为空时等效失配率的估计值，仿真所得α估计值为0.046。

图4为空时等效误差校正前后的目标像对比。图4（a）为校正前的目标像，从图中可以看出，由于存在空时等效误差，目标像在方位向会出现很多的虚假像，造成目标像模糊，成像质量下降，仿真求得图4（a）的图像熵为9.368 7；图4（b）为校正后的目标像，仿真求得图4（b）的图像熵为8.896 5。对比图4（a），图4（b）虚假目标被有效抑制，图像清晰度更高，图像熵更小，成像质量提高，证明了本文提出的空时等效误差校正方法的有效性。

4 结 论

本文针对MIMO-ISAR成像中的空时不等效问题，首先建立了空时等效误差模型，并对模型进行了分析，根据频域重构思想推导出空时等效误差的校正模型，得出误差校正矩阵，且误差校正矩阵只与空时等效失配率有关；利用特显点方位像熵最小的方法估计出空时等效失配率，构建误差校正矩阵，实现了MIMO-ISAR空时等效误差的校正。数值仿真验证了这一方法的有效性。

［1］Pastina D，Santi F，Bucciarelli M.Multistatic and MIMO distributed ISAR for enhanced cross-range resolution of rotating targets［J］.IEEE Trans.on Geoscience and Remote Sensing，2010，48（8）：3300- 3316.

［2］Zhu Y T，Su Y，Yu W X.An ISAR imaging method based on MIMO technique［J］.IEEE Trans.on Geoscience and Remote Sensing，2010，48（8）：3290- 3299.

［3］Pastina D，Santi F，Bucciarelli M.MIMO distributed imaging of rotating targets for improved 2-D resolution［J］.IEEE Geoscience and Remote Sensing Letters，2015，12（1）：190- 194.

［4］Tarchi D，Oliveri F，Sammartino P F.MIMO radar and groundbased SAR imaging systems：equivalent approaches for remote sensing［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（1）：425- 435.

［5］Ma C，Yeo T S，Zhang Q，et al.Three-dimensional ISAR imaging based on antenna array［J］.IEEE Trans.on Geoscience and Remote Sensing，2008，46（2）：504- 515.

［6］Pastina D，Santi F，Bucciarelli M，et al.2D-MIMO SAR／ISAR imaging of moving targets with reconfigurable formation of platforms［C］∥Proc.of the European Conference on Synthetic Aperture Radar，2012：223- 226.

［7］Yang J C，Su W M，Gu H.A method for rearrangement of 2D MIMO-ISAR space-time echo based on 2D frequency estimation［J］.Journal of Electronics&Information Technology，2014，36（9）：2180- 2186.（杨建超，苏卫民，顾红.基于二维频率估计的MIMO-ISAR空时二维回波重排方法［J］.电子与信息学报，2014，36（9）：2180- 2186.）

［8］Ma C，Yeo T S，Zhao Y B.MIMO radar 3D imaging based on combined amplitude and total variation cost function with sequential order one negative exponential form［J］.IEEE Trans. on Image Processing，2014，23（5）：2168- 2183.

［9］Zhu Y T，Yu W X，Su Y.An ISAR imaging method based on MIMO technique［J］.Acta Electronic Asinica，2009，37（9）：1885- 1894.（朱宇涛，郁文贤，粟毅.一种基于MIMO技术的ISAR成像方法［J］.电子学报，2009，37（9）：1885- 1894.）

［10］Zhu Y T，Su Y.A type of M2-transmitter N2-receiver MIMO radar array and 3D imaging theory［J］.Science China Information Sciences，2011，41（12）：1495- 1506.（朱宇涛，粟毅.一种M2发N2收MIMO雷达平面阵列及其三维成像方法［J］.中国科学F辑：2011，41（12）：1495- 1506.）

［11］Ma C Z，Yeo T S，Tan C S，et al.Three-dimensional imaging of targets using colocated MIMO radar［J］.IEEE Trans.on Geoscince and Remote Sensing，2011，49（8）：3009- 3021.

［12］Ma C Z，Yeo T S，Tan C S，et al.Three-dimensional imaging using colocated MIMO radar and ISAR technique［J］.IEEE Trans. on Geoscience and Remote Sensing，2012，50（8）：3189- 3201.

［13］Bucciarelli M，Pastina D.Multi-grazing ISAR for side-view imaging with improved cross-range resolution［C］∥Proc.of the IEEE Radar Conference，2011：939- 944.

［14］Chen G，Gu H，Su W M，et al.Analysis on the effect of nonequivalent relationship between space and time in MIMO-ISAR imaging［J］.Journal of Electronics&Information Technology，2013，35（8）：1806- 1812.（陈刚，顾红，苏卫民，等.空时不等效对MIMO雷达采用ISAR技术成像影响的分析［J］.电子与信息学报，2013，35（8）：1806- 1812.）

［15］Jenq Y C.Perfect reconstruction of digital spectrum from nonuniformly sampled signals［J］.IEEE Trans.on Instrumentation and Measurement，1997，46（3）：649- 652.

胡晓伟（198-7- ），男，博士研究生，主要研究方向为微动特征提取、三维成像。

E-mail：601237134＠qq.com

Space-time equivalent errors correction in MIMO-ISAR imaging

DONG Hui-xu，ZHANG Yong-shun，FENG Cun-qian，HU Xiao-wei
（Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China）

In view of the nonequivalent relationship between the space sampling and time sampling in multiple-input multiple-output inverse synthetic aperture radar（MIMO-ISAR），an space-time quivalent errors model is established and analyzed firstly.Subsequently，a formula which can correct the equivalent errors model between space and time is inferred.The error correction matrix is acquired，which only concerns with the spacetime equivalent miss matched rate.Space-time equivalent miss matched rate is estimated by the minimum crossrange image entropy method.Then the errors correction matrix is structured and space-time equivalent errors are corrected.The simulation results verify the validity of the proposed algorithm.

multiple-input multiple-output inverse synthetic aperture radar（MIMO-ISAR）imaging；spacetime equivalent miss matched rate；space-time equivalent errors correction

TN 957

A

10.3969／j.issn.1001-506X.2015.11.10

董会旭（198-7- ），男，博士研究生，主要研究方向为雷达成像新技术。E-mail：dx19871109＠163.com

张永顺（1961- ），男，教授，博士研究生导师，博士，主要研究方向为雷达阵列信号处理、综合电子战。

E-mail：zhyshun＠yahoo.cn

冯存前（1975- ），男，教授，硕士研究生导师，博士，主要研究方向为雷达成像、微动特征提取。

E-mail：fengcunqian＠sina.com

1001-506X（2015）11-2487-05

2014- 12- 04；

2015- 04- 13；网络优先出版日期：2015- 07- 07。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150707.1401.004.html

国家自然科学基金（61382166）；陕西省自然科学基础研究计划（2014JM8308）资助课题