同轴线馈电的球面共形微带天线的数值分析

于 涛，尹成友，刘 汉

（电子工程学院脉冲功率激光国家重点实验室，安徽合肥230037）

同轴线馈电的球面共形微带天线的数值分析

于 涛，尹成友，刘 汉

（电子工程学院脉冲功率激光国家重点实验室，安徽合肥230037）

采用基于矩量法（method of moments，Mo M）的面 线积分方程法分析了同轴线馈电的球面共形微带天线的输入阻抗。面 线积分法在分析过程中具有未知量少，计算时间短的优势。天线贴片电流和探针电流分别采用Rao-Wilton-Glisson（RWG）基函数与三角基函数来模拟。在线面连接处，提出一种新型的连接基函数以保证探针与贴片的电流连续性。激励源采用磁流环模型，并且结合球表面磁并矢格林函数求解激励源在天线表面产生的场。最后，通过实例验证了连接基函数的可行性，并分析了两副球面共形微带天线的输入阻抗，证明所提分析处理的正确性。

球面共形微带天线；面 线积分方程；连接基函数；同轴线激励；数值分析

0 引 言

众所周知，微带天线具有共形于载体表面而不影响载体动力学性能的优势，成为科研工作者的研究热点之一。目前，共形微带天线的研究主要以圆柱［1］、球形［2］、锥形［3］等规则形状为主，而研究方法主要以精确度较高、复杂性大的全波分析为主，例如时域有限差分法（finite difference time domain，FDTD）、矩量法（method of moments，Mo M）等。

采用Mo M分析共形微带天线性能时，一般采用两种方式。一种方式采用体 面积分方程法［4］，将天线整体剖分，即介质体采用四面体剖分，金属面采用三角形剖分，探针采用线段剖分。这种方式过程简单，理论上可以分析任何形状的共形微带天线，但只适合分析尺寸较小的微带天线，当天线尺寸过大时会产生较多未知量，使得计算效率低下甚至超出计算机内存，需要采用各种快速且节省内存的算法［5-6］，过程较为复杂。另一种方式采用面 线积分方程法［7］，相比第一种方法，这种方式只需要将金属贴片和探针剖分，介质体和接地球体的影响体现在分层媒质中的并矢格林函数里。该方法大大减少了未知量的数目，适用于较大尺寸的天线分析，但求解分层媒质格林函数过程稍显复杂。纵观两种方法各存在优缺点，需要根据具体问题采取不同的方式。

本文采用面 线积分方程法分析了较大尺寸的球面共形微带天线的输入阻抗，以避免内存不足的问题。金属贴片和探针上电流分别采用Rao-Wilton-Glisson（RWG）基函数和三角基函数模拟。针对线面连接处以往分析的不便性，提出了一种新型的连接基函数，有效避免了分析过程的复杂性。采用同轴线馈电等效磁流环激励的方式，推导出磁并矢格林函数的表达式以及磁流环在天线上产生的场量。通过计算两副球面共形微带天线的输入阻抗，与文献结果进行对比，说明了分析处理的正确性与有效性。

1 Mo M分析

研究的天线模型如图1所示。第3层导体球半径为r1，介质层厚度为h，第1层为空气层。同轴线外径为b，内径为a，探针为同轴线内导体的简单延伸。同轴线建模通常建立在接地平面上，在同轴线开口处场分量可以近似为只存在横电磁波。这里同轴线外径b相对于半径r1很小，因此可以近似认为只存在横电磁波。实际使用时，接地金属球体为中空的，上下两端各开一个小孔，作为馈电通道。

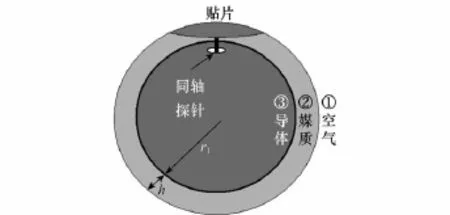
图1 球面共形微带天线示意图

根据天线表面切向场连续，在贴片与探针表面采用伽略金检验的Mo M，有面 线积分方程

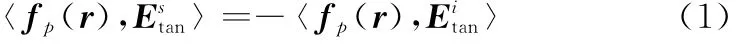
式中，fp（r）为检验函数；为天线表面电流在天线表面（包含贴片和探针）产生场的切向分量；为同轴线激励等效的磁流环在天线表面产生场的切向分量。在本文中

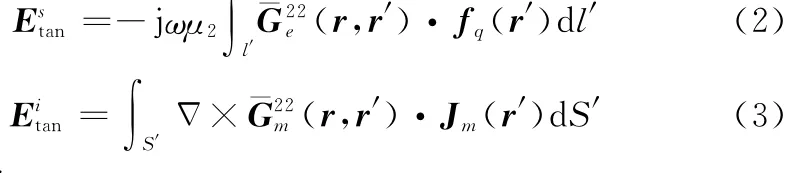
式中，fq（r′）为定义在天线表面的电流基函数；μ2为介质层的磁导率；Jm（r′）为探针底端的磁流；（r，r′）为源点和场点同在介质层时的电并矢格林函数（r，r′）为磁并矢格林函数。上标代表了源场点所在的层数。文献［8］采用矢量波函数法研究了简单的球面边界格林函数，后经学者不断研究完善［9-10］，得到了任意层数的并矢格林函数。笔者采用德拜位同样得到球面分层媒质并矢格林函数，并进行有效的处理［11-12］，这里不再做具体介绍。球面分层媒质中格林函数的通式为

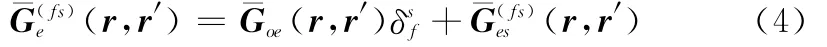
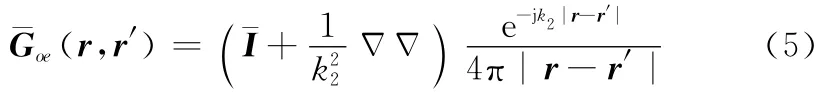
式中，¯I为单位张量。由式（1）可以求出天线的表面电流，鉴于并矢格林函数分成两项处理，阻抗矩阵元素可以表达为

式中，Z1pq为单一媒质中格林函数的贡献；Z2pq表示反射透射效应格林函数的贡献。经化简，这两项可以表示为

V矢量可以表达为

2 连接基函数

基函数的选择是Mo M计算中不可或缺的一部分。针对贴片表面电流采用了RWG基函数模拟，而探针可以采用细条带等效。细条带等效探针具有一定的方便性，利用RWG函数可以很容易保证贴片与探针的电流连续性，只是馈电边为探针与接地球的公共边，由于接地球体并不进行三角形剖分，因此馈电边不是RWG函数的公共边，需要引入边界电荷来保证电荷守恒［15］。文献［16］引言中也阐述了馈电的另外一种模型，采用细线代替探针进行分析。这种模型与实际同轴线模型相符，但存在两方面困难：一方面为线面连接基函数的分析；另一方面为探针底部激励源的处理。

这里主要解决上述两个方面的困难。采用细线段表示探针，探针上采用三角基函数。贴片上采用RWG函数。对于探针与贴片连接处，需要一种特殊的连接基函数以保证电流的连续性。目前较为常用的连接基函数［17-18］如图2所示，探针与贴片的连接点位于多个贴片三角形汇聚的公共点，其表达式为

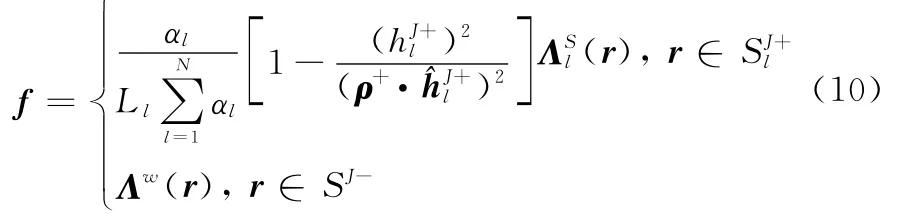
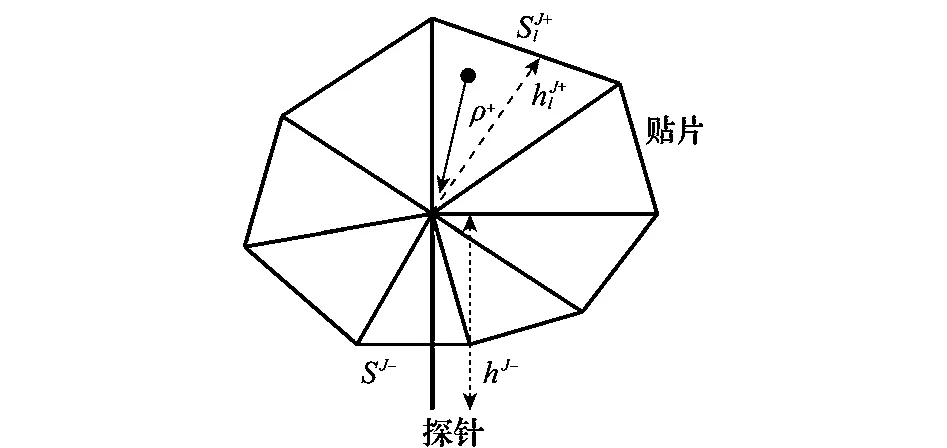
图2 常见的线面模型

这种基函数满足连接基函数的条件，公式复杂，最大的难点在于连接点处的奇异性［17］，当ρ＋→0，基函数本身趋于无穷大。处理奇异性无疑增加了分析的复杂度［18］。

本文提出了一种新型的连接基函数，如图3所示，该基函数要求探针并不位于三角形汇聚的公共点上，而是位于两个三角形的公共边上，这种基函数启发于面面相连的结构，可以表示为

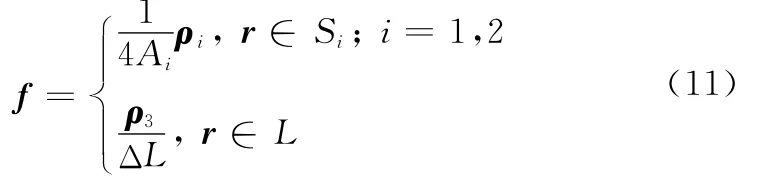
式中，ΔL表示三角基函数所在线段的长度；ρ1、ρ2代表三角形中的点到顶点的矢量；ρ3为线段端点到线段上点的矢量；Ai表示三角形的面积。

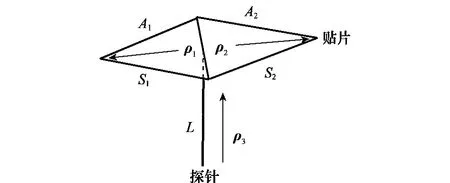
图3 本文连接处模型

根据面散度定理

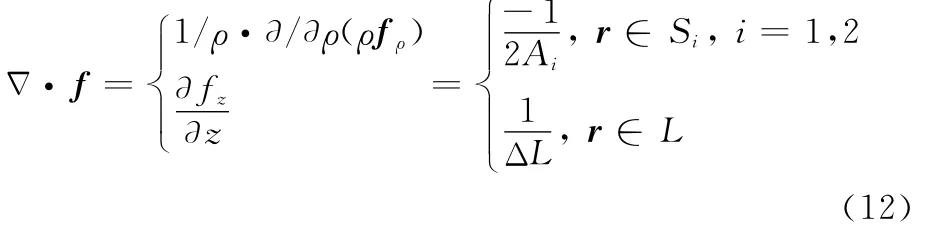
三角形上的电荷量为

线段上的电荷量为

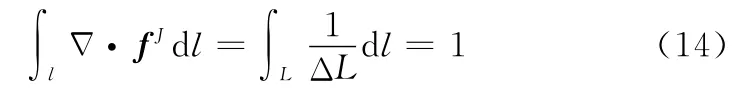
因此，连接基函数总的电荷为零。从上式可以看出，该模型最大的优点是：连接基函数表达式接近于RWG函数，且不存在表达式上的奇异性，对于数值计算中的奇异性可以采用与RWG函数相同的处理方法，不需要单独处理。

通过上面的论述可知，3类基函数用来表示天线表面电流，即RWG基函数、三角基函数和连接基函数，分别模拟贴片、探针以及连接处的电流分布。因此，Mo M中的矩阵等式可以表示为

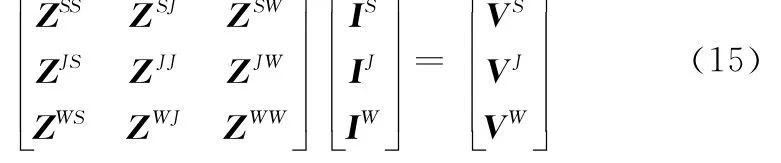
即阻抗矩阵Z分为9大部分，上标S、J、W分别代表面、连接处以及线段。将所在位置的基函数代入式（7）和式（8）计算，求解相应位置的阻抗元素，需要说明的是，三角形上积分可以采用高斯积分，在线段上精确积分可以采用椭圆积分的形式［19］。

3 激励源的处理

对激励源的处理，是为了得到式（9）中的V矢量。采用同轴线激励的方式，近似考虑同轴线内只存在横电磁波，则在同轴线顶端形成磁流环［20］，如图4阴影区所示。

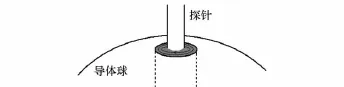
图4 激励源处放大图

在阴影区的场为

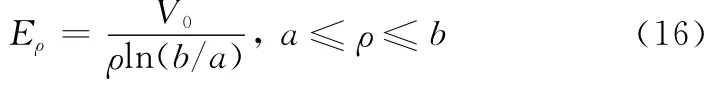
式中，V0为同轴线的输入电压。下标ρ代表柱坐标系，而这里必须采用球坐标系，考虑到b≪r1，且同轴线位于Z轴上，则Eθ≈Eρ。

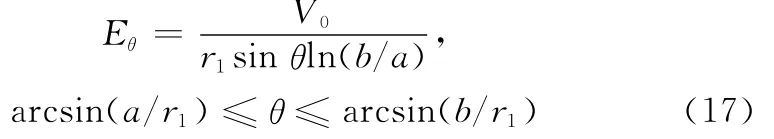
根据边界条件，球表面阴影区的磁流为

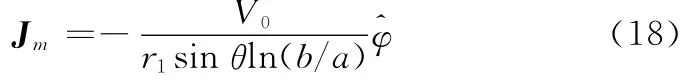
在无穷大平面情况下，一般会根据镜像法等效成两倍磁流大小，然后求解磁流环产生的场。这里为了计算的精确性，不把曲面近似成平面。磁流环在单一媒质内天线轴向方向上产生的场［21］为

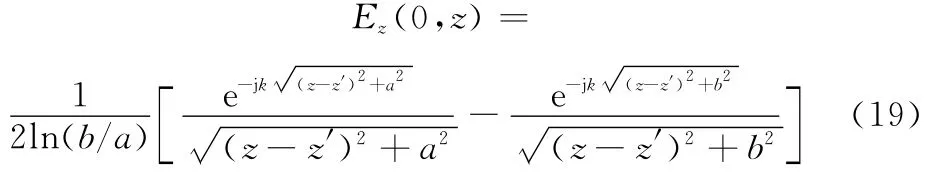
自由空间内磁流环在天线的非轴向方向上产生的场较为复杂，这里不再给出其具体表达式，可以参考文献［21］。

而对于反射透射效应并矢格林函数的场贡献，有

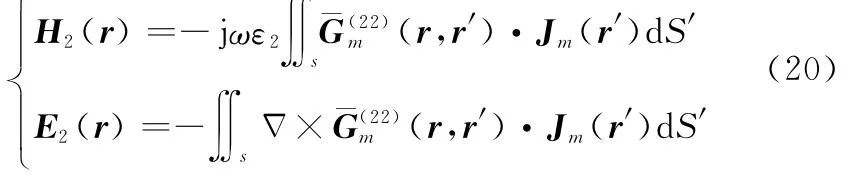
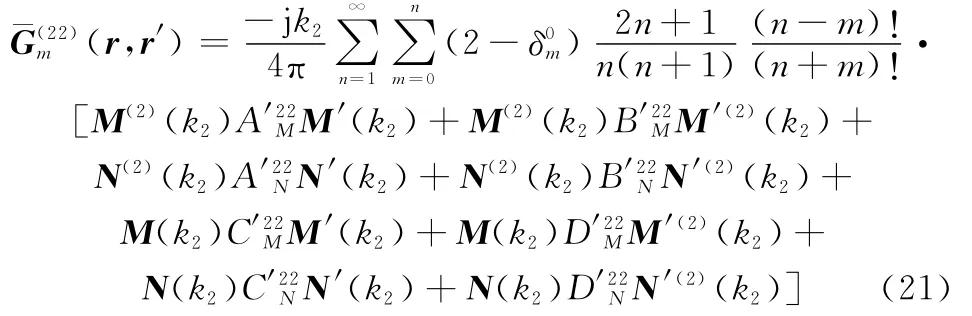
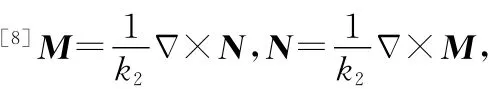
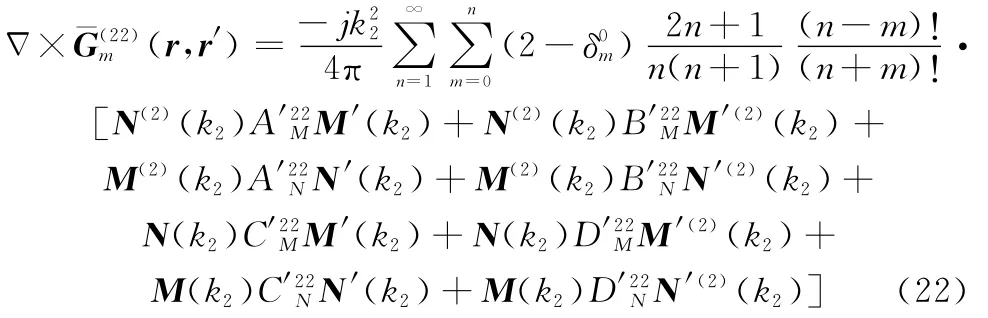
结合此处磁流源只有^φ分量，只需要求解式（22）的，，分量，将矢量波函数代入展开，以^r^φ为例，经复杂代数计算得

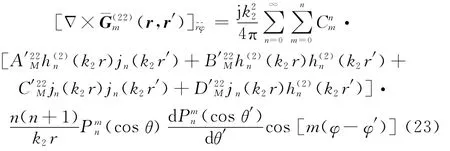
式（20）可进一步表示为

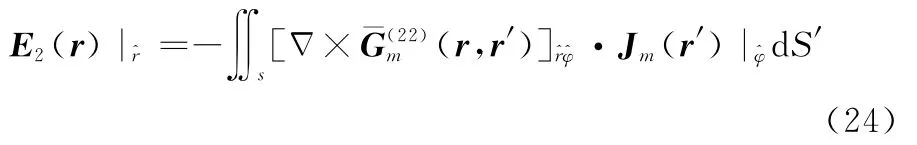
式中，Jm（r′）位于球表面，对于表面积分，首先对φ′进行积分，积分上下限为0～2π，再对θ′积分，积分区域为arcsin（a／r1）～arcsin（b／r1）。对进行积分时，可以发现当m≠0时积分全部为0，只有m＝0时存在积分值，而且d S′＝sinθ′ddθ′，则式（24）经化简可以表达为

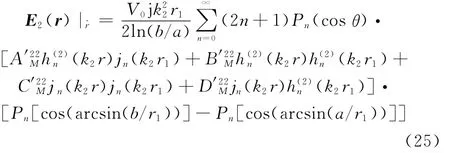
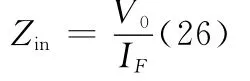
式中，IF为馈电处的电流值。

4 计算结果

首先，为了验证连接基函数的可行性，本文计算了一副位于长方体表面的单极子天线，如图5所示，单极子天线的长度为83.8 mm，半径为1 mm，金属长方体的长宽分别为83.8 mm、116.7 mm，高为150 mm。单极子天线位于中心位置。计算的输入阻抗的实部和虚部分别如图5和图6所示。

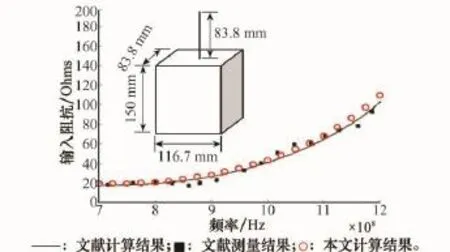
图5 单极子输入阻抗实部

图6 单极子输入阻抗虚部

通过验证可以看出，本文连接基函数模型算得结果与文献［22］模型结果以及实测结果相吻合，证明了本文所提模型的可行性。本文的处理过程要比文献方法简便得多。

经过上述分析，计算了一副球面共形微带天线的输入阻抗，天线的示意图如图1所示。球体的半径为5 cm，介质厚度为0.32 mm，共形贴片的弧半径为1.88 cm，激励探针距离天线中心为0.94 cm，介质的相对介电常数εr＝2.47，相对磁导率μr＝1，探针半径0.5 mm。计算的输入阻抗与文献其他方式得到的结果相吻合，如图7所示，采用Photoshop软件将图拟合在一起，图中R表示输入阻抗的实部，X表示输入阻抗的虚部，计算结果验证了分析的正确性。

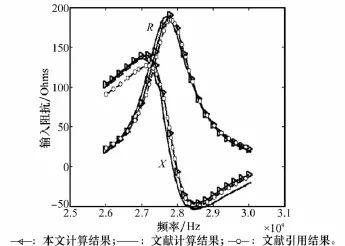
图7 与文献［9］输入阻抗对比图

为进一步验证分析的正确性，分析矩形贴片微带天线的输入阻抗，球体半径为18.5 cm，矩形贴片尺寸5.1 cm× 5.1 cm，介质为泡沫塑料，介电常数约为1，厚度为0.52 cm。探针距离贴片中心为1.95 cm。计算的输入阻抗与文献［2］实测结果相吻合，如图8所示，验证了本文计算的正确性。

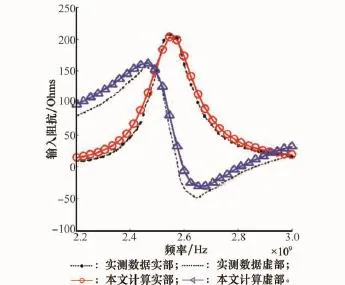
图8 与文献［2］实测数据对比图

5 结 论

采用Mo M分析了球面共形微带天线的输入特性。采用RWG基函数和三角基函数模拟天线表面电流，针对线面连接处电流的连续性，提出一种新型的连接基函数，有效降低了研究的复杂度。采用同轴线馈电等效磁流环激励的方式，推导出磁并矢格林函数的表达式以及磁流环在天线上产生的场量。分析了两副球面共形微带天线的输入阻抗，结果与文献结果相吻合，说明了本文分析处理的正确性与有效性。

［1］Arkadiusz B，Pawel K，Fritz B，et al.Sectorial cylindrical patch antenna for broadband at sea wireless nodes installed on vessels［C］∥Proc.of the International Symposium on Antennas and Propagation，2012：227- 230.

［2］Sipus Z，Burum N，Skokic S，et al.Analysis of spherical arrays of microstrip antennas using moment method in spectral domain［J］.IEE Proceedings Microwave Antennas Propagation，2006，153（6）：533- 543.

［3］He M，Xu X W，Lu Q.Application of conformal FDTD algorithm to analysis of conically conformal microstrip antenna［C］∥Proc.of the International Conference on Microwave and Millimeter Wave Technology，2008：1- 4.

［4］Zhang K，He M，Xu X W，et al.An efficient solution of the volume-surface integral equation for electromagnetic scattering and radiation of the composite dielectric-conductor objects with reduced number of unknowns［J］.IEEE Trans.on Antennas and Propagation，2013，61（2）：798- 808.

［5］Wang Z G，Sun Y F，Wang G H.Analysis of electromagnetic scattering characteristics from con-ducting targets using improved fast dipole method and characteristic basis function method［J］.Journal of Electronics&Information Technology，2013，35（9）：2272- 2276.（王仲根，孙玉发，王国华.应用改进的快速偶极子法和特征基函数法分析导体目标电磁散射特性［J］.电子与信息学报，2013，35（9）：2272- 2276.）

［6］Hu J，Li Y K，Nie Z P，et al.Modal characteristic basis function method for solving scattering from multiple conducting bodies of revolution［J］.IEEE Trans.on Antennas and Propagation，2014，62（2）：870- 877.

［7］Wu J，Khamas S K，Cook G G.Moment method analysis of a conformal curl antenna printed within layered dielectric cylindrical media［J］.IEEE Trans.on Antennas and Propagation，2013，61（7）：3912- 3917.

［8］Dai Z D，Lu S.Dyadic Green’s functions in electromagnetic theory［M］.Wuhan：Wuhan University Press，2005.（戴振铎，鲁述.电磁理论中的并矢格林函数［M］.武汉，武汉大学出版社，2005.）

［9］Li L W，Kooi P S，Leong M S，et al.Electromagnetic dyadic Green’s function in spherically multilayered media［J］.IEEE Trans.on Microwave Theory and Techniques，1994，42（12）：2302- 2310.

［10］Khamas S K.Electromagnetic radiation by antennas of arbitrary shape in a layered spherical media［J］.IEEE Trans.on Antennas and Propagation，2009，57（12）：3827- 3834.

［11］Yin C Y，Yu T，Tang W.Solving dyadic Green’s functions for spherically multilayered media I：introduction of dyadic Green’s functions［J］.Journal of Microwave，2014，30（3）：9- 14.（尹成友，于涛，唐伟.球形分层媒质中并矢格林函数的求解I：并矢格林函数的推导［J］.微波学报，2014，30（3）：9- 14.）

［12］Yu T，Yin C Y.Solving dyadic Green’s functions for spherically multilayered media II：fast calculation for dyadic Green’s functions［J］.Journal of Microwave，2014，30（4）：20- 24.（于涛，尹成友.球形分层媒质中并矢格林函数的求解II：并矢格林函数快速计算［J］.微波学报，2014，30（4）：20- 24.）

［13］Khamas S K.Asymptotic extraction approach for antennas in a multilayered spherical media［J］.IEEE Trans.on Antennas and Propagation，2010，58（3）：1003- 1008.

［14］Yu T，Yin C Y，Liu H Y.Analysis for probe-fed microstrip antennas in multilayered spherical media based on Mo M［J］.Journal of Applied Sciences，2013，31（5）：544- 550.（于涛，尹成友，刘海义.探针馈电的分层球状微带天线矩量法分析［J］.应用科学学报，2013，31（5）：544- 550.）

［15］Yu T，Yin C Y.Establishment of thin strip feed model for spherical microstrip antenna analysis［J］.Systems Engineering and Electronics，2014，36（9）：1712- 1716.（于涛，尹成友.球状微带天线分析中细条带馈电模型的构建［J］.系统工程与电子技术，2014，36（9）：1712- 1716.）

［16］Hwu S U，Wilton D R，Rao S M.Electromagnetic scattering and radiation by arbitrary conducting wire-surface configuration［C］∥Proc.of the IEEE International Symposium Digest on Antennas and Propagation Society，1988：890- 893.

［17］Guo J L，Liu Q Z，Zhou B.Conical monopole antennas on finite ground planes［J］.Acta Electronica Sinica，2005，33（3）：560- 562.（郭景丽，刘其中，周斌.有限导体地面上的圆锥单极子天线［J］.电子学报，2005，33（3）：560- 562.）

［18］Francesca V，Wilton D R.Optimized numerical evaluation of singular and near-singular potential integrals involving junction basis functions［J］.IEEE Trans.on Antennas and Propagation，2011，59（1）：162- 171.

［19］Wilton D R，Champagne N J.Evaluation and integration of the thin wire kernel［J］.IEEE Trans.on Antennas and Propagation，2004，54（4）：1200- 1206.

［20］Ted S.The magnetostatic frill source［J］.IEEE Trans.on Antennas and Propagation，2011，59（9）：3313- 3317.

［21］Hui H T，Edward K N Y，Chan K Y.On the numerical calculation of the magnetic current frill model［J］.Radio Science，2001，36（6）：1683- 1686.

［22］Wan J X，Zhang Y，Liang C H.Method of moment analysis of connect between wire antennas and arbitrary shape conductors［J］.Chinese Journal of Radio Science，2003，18（5）：523- 528.（万继响，张玉，梁昌洪.任意导体与线天线连接问题的Mo M分析［J］.电波科学学报，2003，18（5）：523- 528.）

于 涛（198-6 -），男，博士研究生，主要研究方向为电磁场理论、共形微带天线的理论研究和数值分析。

E-mail：yutaosunxiaoyan＠126.com

尹成友（1964 -），男，教授，博士研究生导师，博士，主要研究方向为天线与电波传播、近地复杂线天线分析、微带天线理论及数值分析、数据融合及阵列信号处理。

E-mail：cyouyin＠sina.com

刘 汉（198-8- ），男，博士研究生，主要研究方向为超宽带微带天线的理论分析与仿真计算。

E-mail：lujiangliuhan＠sina.com

Numerical analysis of spherical conformal microstrip antenna fed by coaxial line

YU Tao，YIN Cheng-you，LIU Han
（State Key Laboratory of Pulsed Power Laser Technology，Institute of Electronic Engineering，Hefei 230037，China）

The input impedance of spherical conformal microstrip antennas fed by the coaxial line is analyzed using the surface-wire integral equation method based on method of moments（Mo M）.The surface-wire integral equation method has advantages of few unknowns and short calculation time in the analysis process.The equivalent currents on the antenna patch and probe are simulated by the Rao-Wilton-Glisson（RWG）basis function and the triangle basis function respectively.A novel junction basis function is proposed at the junction to keep the current continuity from patch to probe.The field on the surface of the antenna produced by magnetic frill source is calculated based on the magnetic dyadic Green’s functions.Finally，the junction basis function is validated in terms of feasibility，and the input impedance of spherical conformal microstrip antennas are analyzed based on two examples.Calculated results show the validity of the proposed method.

spherical conformal microstrip antenna；surface-wire integral equation；junction basis function；coaxial line extraction；numerical analysis

TN 520

A

10.3969／j.issn.1001-506X.2015.11.02

1001-506X（2015）11-2432-06

2014- 12- 24；

2015- 05- 02；网络优先出版日期：2015- 06- 18。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150618.0908.005.html

总装备部预研基金资助课题