伸缩翼飞机变形飞行的建模与滑模变增益控制

殷 明，陆宇平，姚克明，2，何 真

（1.南京航空航天大学自动化学院，江苏南京210016；2.江苏理工学院电气信息工程学院，江苏常州213001）

伸缩翼飞机变形飞行的建模与滑模变增益控制

殷 明1，陆宇平1，姚克明1，2，何 真1

（1.南京航空航天大学自动化学院，江苏南京210016；2.江苏理工学院电气信息工程学院，江苏常州213001）

研究了伸缩翼飞机变形飞行过程的动力学建模与鲁棒控制问题，以分析机翼变形对飞机性能的影响机理，并实现机翼变形时的平稳飞行。首先通过气动仿真分析构建了伸缩翼飞机气动参数与机翼变形的关联函数，进而建立了变形飞行的动力学模型。在此基础上提出了一种新的滑模变增益控制（sliding mode gain-scheduled control，SMGSC）策略，更好地保证闭环系统的全局稳定和鲁棒性能。仿真结果表明，机翼伸缩能直接改变飞机的气动特性和运动模态；SMGSC能更好地保持伸缩翼飞机变形飞行时的状态稳定，并消除复合干扰的影响；伸缩翼飞机通过机翼变形可以减少50%的燃油消耗实现同样的飞行任务，具有重要的性能优势。

伸缩翼飞机；变形飞行；动力学建模；滑模变增益控制；燃油消耗

0 引 言

可变形飞行器是指能够在飞行中实时改变部分外形结构的飞行器，变形方式包括翼面鼓包、翼梢扭转、机翼伸缩、折叠、后掠等［1］。由于其具有调节气动性能，满足多任务需求的潜在能力，已成为国内外飞行器研究的热点方向。

美国NASA、DARPA等机构自20世纪末期开始有关可变形飞行器的科研计划［2-4］，近些年一些国内外大学也开展了各自的研究［5-9］。这些研究大多集中于变形机构自身的设计与实现，对于变形对飞行器性能的实际影响分析尚不完善，而如何在飞行器实施变形的同时保持平稳飞行更成为亟待研究的问题。由于变形对飞行器结构的改变，变增益控制［1012］成为可能的选择，但其受工作区间网格划分和控制器插值方法的影响，不一定能保证全局稳定与鲁棒性能。考虑到变形飞行的强耦合、非线性、不确定性等特点，一些先进控制策略，如切换控制［13］、鲁棒控制［14］、自适应控制［1516］等得到初步应用，但当存在较大干扰时，控制效果将难以保证。借助滑模控制的强鲁棒性和滑模面的可达性［17］，滑模干扰观测器被设计用于估计系统干扰和进行补偿控制［18］，并在高超声速飞行器［19］、光电跟踪系统［20］等对象中得到了一定应用。

本文研究了一款伸缩翼飞机在机翼变形时保持平稳飞行的建模与控制问题。首先仿真计算机翼伸缩时的飞行器气动参数，建立变形与气动的关联函数模型；进而构建伸缩翼飞机纵向非线性模型，其中包含机翼变形的因素，并转换为线性变参数（linear parameter-varying，LPV）形式，分析机翼伸缩对飞行器性能的影响机理。针对变形过程的不确定性和外部干扰，提出一种新的滑模变增益控制（sliding mode gain-scheduled control，SMGSC）策略，避免一般网格划分和插值选择对控制设计的影响，同时利用滑模干扰观测进行补偿控制，保证伸缩翼飞机变形飞行过程的全局稳定，并更好地抑制复合干扰。最后通过数值仿真验证所设计的SMGSC的优越性，并说明伸缩翼飞机的性能优势。

1 伸缩翼飞机气动建模与变形飞行动力学分析

以美国L-17教练机（见图1）为伸缩翼飞机原型，设定其能够在飞行中同步伸长或缩短两侧机翼（见图2），并且最长翼展是最短翼展的两倍。伸缩翼飞机的基本属性见表1。定义翼展变形率ξ＝Δb／bmin表示机翼伸缩的程度，其中bmin是最短翼展，Δb是翼展变形量，从而ξ∈［0，1］。

图1 美国L-17教练机

图2 机翼伸缩示意图

1.1 机翼伸缩时的气动参数仿真与建模

为分析机翼伸缩对飞机气动特性的影响，通过Datcom气动分析软件仿真计算伸缩翼飞机在飞行包线内不同工作点、不同ξ下的各项气动参数，将所得全部数据导入Matlab，并进行相应拟合处理，得到升力系数CL、阻力系数CD、俯仰力矩系数Cm，分别表示为

式中，α为迎角；q为俯仰角速度；V为飞行速度；δe为升降舵偏角。

表1 伸缩翼飞机基本属性

进一步分析式（1）中的各项气动参数，发现其主要受翼展变化和飞行速度的影响，进而通过最小二乘拟合方法建立气动参数与翼展变形率ξ和马赫数Ma的关联函数

式（1）和式（2）的研究结果表明，相比常规飞机，伸缩翼飞机的气动参数还与ξ密切相关，即机翼伸缩能直接改变飞机自身的气动特性，这是其与常规飞机的重要区别。

1.2 伸缩翼飞机变形飞行的动力学建模

建立了与机翼伸缩相关的气动参数函数之后，进而构建伸缩翼飞机变形飞行的纵向非线性动力学模型

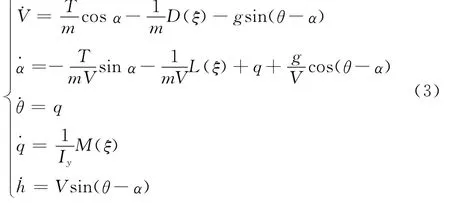
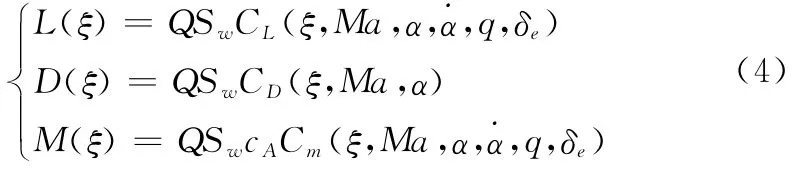
式中，Q为动压；各气动系数是第1.1节建立的气动参数函数。

分析式（3）、式（4）可知，伸缩翼飞机的动力学模型中增加了机翼变形的因素，这表明在变形飞行时由于机翼伸缩引起额外的气动特性变化，产生附加的动力学效应，将会影响整体的飞行趋势。这种变形与飞行的耦合关联正是可变形飞行器的本质特点，也是控制器设计的重点。

根据非线性系统LPV建模的Jacobian线性化方法［21］，对伸缩翼飞机非线性模型式（3）在飞行包线内各工作点分别进行线性化处理，再经过拟合、化简，建立变形飞行LPV模型

式中，状态变量x＝［ΔV，Δα，Δθ，Δq，Δh］T；输入变量u＝［Δδe，Δδt］T；各矩阵系数分别为

考虑到建模误差、外部干扰以及机翼伸缩引起的附加不确定性等因素，将伸缩翼飞机变形飞行LPV模型式（5）进一步表述为

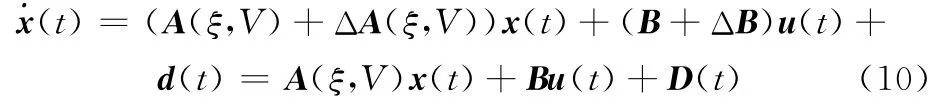
式中，D（t）＝ΔA（ξ，V）x（t）＋ΔBu（t）＋d（t）称为复合干扰。

1.3 机翼伸缩对飞机性能的影响分析

分析伸缩翼飞机LPV模型式（10），可知在飞行包线内，改变飞机特性、影响飞机性能的主要参数是飞行速度和机翼伸缩。进一步分析变形飞行时式（10）的系统特征根的变化情况（以飞行速度60 m／s，飞行高度3 km为例，如图3所示），发现飞机的纵向运动模态随着机翼伸展而发生迁移，特别是长周期模态由稳定区域逐渐进入到不稳定区域。这表明，在飞行速度、高度不变的情况下，仅靠伸缩机翼就能明显改变飞机自身的系统特性，这种改变是机翼伸缩对飞机性能的本质影响，也是常规飞机所没有的特点。

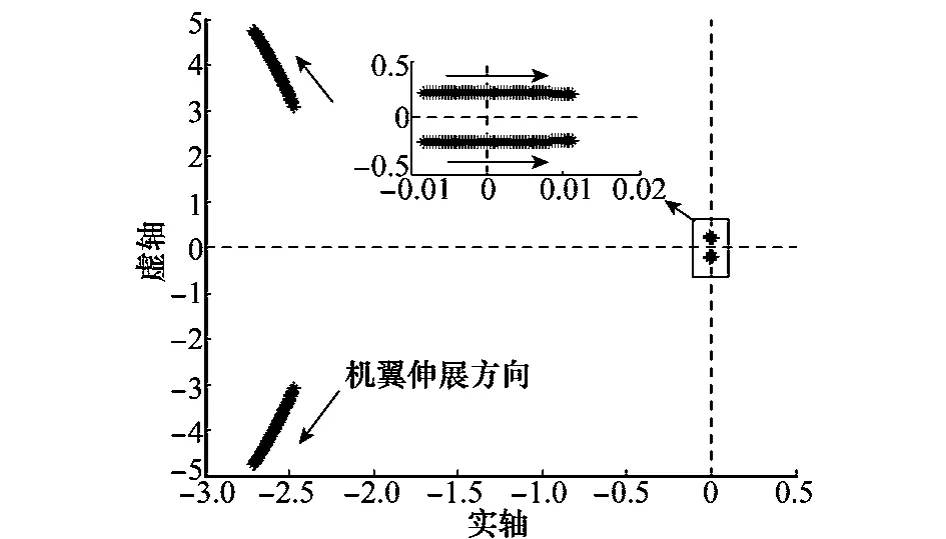
图3 伸缩翼飞机变形飞行的纵向运动模态变化趋势

2 滑模变增益控制器设计

一般的变增益控制需要划分系统工作区间，选择若干工作点分别设计控制器，并通过插值方式实现全局控制［10-12］。由于没有统一的划分与插值原则，因此设计过程复杂，全局稳定和鲁棒性也不一定能得到保证。针对伸缩翼飞机变形飞行的不确定性和外部干扰，并结合LPV模型式（10）的仿射结构，本节提出一种基于滑模干扰补偿的变增益控制策略SMGSC，无需网格划分与控制插值，能从理论上保证系统在整个变参空间的全局稳定，并通过对复合干扰的观测估计提供鲁棒控制能力。

2.1 SMGSC设计与结构

不失一般性，考虑一类不确定LPV系统

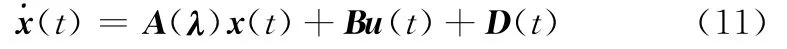
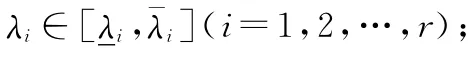
对于LPV系统式（11），控制器设计的目标是：

（1）保证闭环系统在λ的整个变化范围内都是全局稳定的；

（2）保证闭环系统具有对复合干扰的鲁棒抑制能力。

根据上述设计目标，本文提出如下结构的SMGSC：

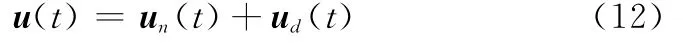
该控制器包括两个部分：un（t）是变增益控制部分，目的是保证闭环系统在全局内稳定；ud（t）是滑模干扰补偿控制部分，目的是观测复合干扰并提供补偿控制。

图4给出了将SMGSC式（12）引入伸缩翼飞机变形飞行非线性模型式（3）后的控制系统结构。

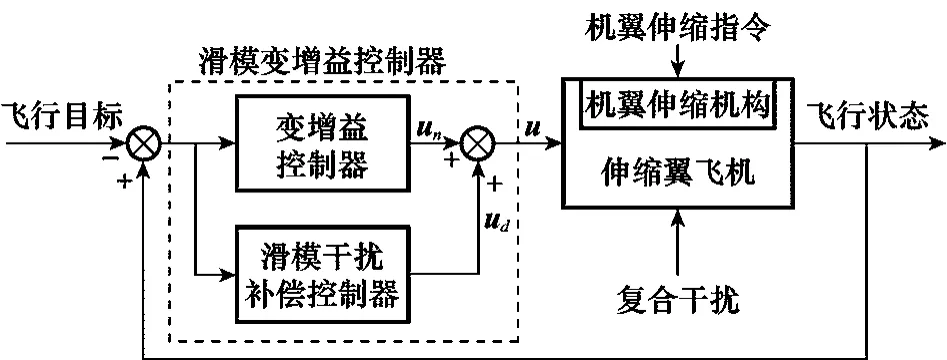
图4 伸缩翼飞机变形飞行控制系统结构

SMGSC式（12）的具体结构为

式中，K（λ）＝K0＋λ1K1＋…＋λrKr；B＋是B的M-P广义逆；v（t）＝［v1（t），v2（t），…，vn（t）］T是复合干扰D（t）的滑模观测值。

2.2 闭环系统稳定性分析

将SMGSC式（12）代入LPV系统式（11），得到闭环系统

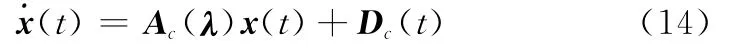
式中，Ac（λ）＝A（λ）－BK（λ）为标称闭环系统矩阵；Dc（t）为复合干扰观测误差。

定理1对于不确定LPV系统式（11），构造辅助滑模变量S（t）＝［S1（t），S2（t），…，Sn（t）］T

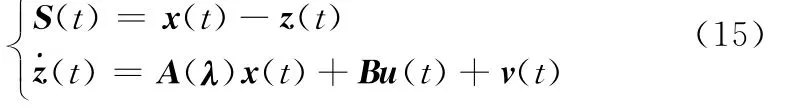
式中

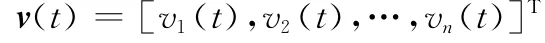
并且

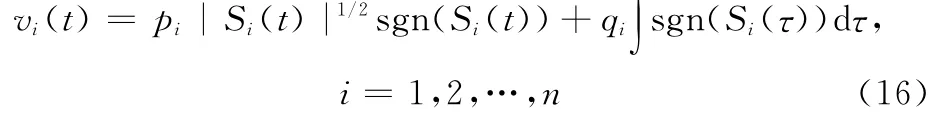
如果存在对称正定实矩阵P和实矩阵Qj（j＝0，1，…，r），满足下述2r个线性矩阵不等式（linear matrix inequality，LMI）条件

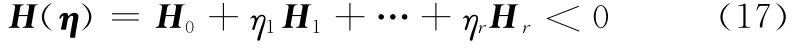
式中

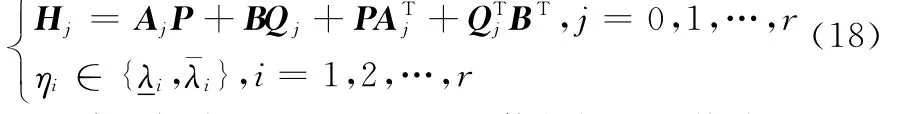
则可以设计形如式（12）的SMGSC，使得闭环系统式（14）对于所有可能的λ都是全局二次稳定的，并且具有对复合干扰的鲁棒性。此时，SMGSC式（12）的设计参数为

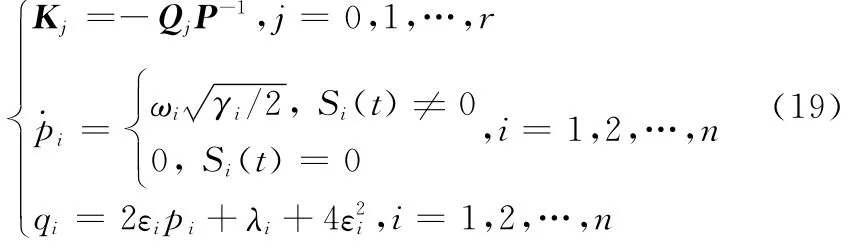
式中，ωi，γi，εi，λi（i＝1，2，…，n）为任意正的常数。

证明首先证明闭环系统式（14）具有对复合干扰的鲁棒性。

对辅助滑模变量式（15）求导，得到

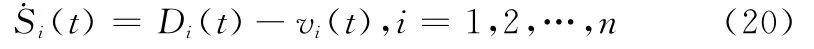
将式（16）代入式（20），得到

根据自适应超扭曲算法理论［22-23］，当式（21）的参数选择满足式（19）的条件时，辅助滑模变量Si（t）及其导数（t）均可在有限时间内收敛至0，表明vi（t）能观测到Di（t）的实际值，从而闭环系统干扰估计误差Dc（t）可在有限时间内收敛至0，即对复合干扰具有极高的鲁棒性。

其次证明闭环系统式（14）对所有可能的λ都是全局二次稳定的。由于复合干扰观测误差能在有限时间内收敛至0，因此只需证明标称闭环系统的全局二次稳定性。

如果式（17）的LMI条件有解，那么根据凸理论［10］，对于所有可能的λ均成立

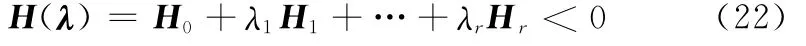
将式（18）和式（19）代入式（22），整理得到

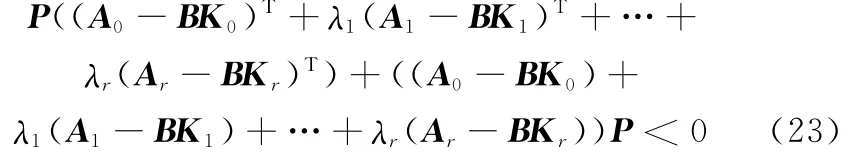
即

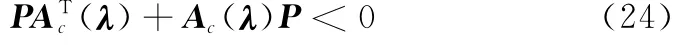
对式（24）进行相合变换，得到

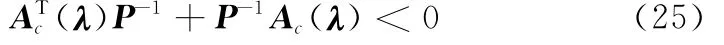
满足Lyapunov二次稳定性要求［10］，因此闭环系统对所有可能的λ都是全局二次稳定的。

证毕

定理1的SMGSC构造中借鉴了自适应超扭曲滑模观测器的设计理念［22-23］，实现了辅助滑模变量及其一阶导数在有限时间内收敛到0，并避免了一般超扭曲算法中需要预先获得未知干扰导数上界的局限性［24-25］。

3 伸缩翼飞机变形飞行仿真与分析

为检验所设计的SMGSC对伸缩翼飞机变形飞行的控制效果，设定如下仿真过程：伸缩翼飞机在3 km高度以0.15Ma（49.3 m／s）的速度平飞，根据机翼伸缩指令在30 s内从最短翼展（ξ＝0）逐渐伸长至最长翼展（ξ＝1），保持20 s后再逐渐收缩回最短翼展；整个过程中始终保持飞行速度与高度的稳定。为考察SMGSC的鲁棒性能，在翼展伸展完成后加入1 000sin t N的干扰力和8000sin t N·m的干扰力矩，同时飞机参数加入10%的不确定性。

3.1 控制器参数设计

根据定理1，对伸缩翼飞机LPV模型式（10）设计形如式（12）的SMGSC，首先依据伸缩翼飞机设计范围ξ∈［0，1］和V∈［30 m／s，70 m／s］，通过Matlab解算LMI约束条件式（17），获得一组可行解，并结合不确定性和外部干扰的情况选择合适的滑模观测器参数，经过仿真调试，最终确定SMGSC的参数设计为

3.2 仿真结果与分析

将第3.1节设计的SMGSC引入伸缩翼飞机变形飞行的原始非线性动力学模型式（3），构成闭环系统，仿真期望的飞行过程。同时采用切换变增益控制与最优控制方法仿真同样的变形飞行过程以作对比。

机翼伸缩指令与实际响应如图5所示。

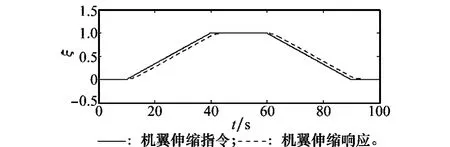
图5 机翼伸缩指令与实际响应

伸缩翼飞机变形飞行过程的仿真结果如图6所示。

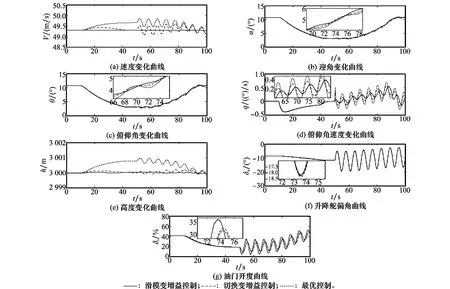
图6 伸缩翼飞机变形飞行过程图

3.2.1 无复合干扰情况

由图6可知，在未加入复合干扰的机翼伸展过程中，最优控制器下的伸缩翼飞机直接偏离了原先的飞行速度与高度；切换变增益控制器下虽然最终能回到原先状态，但也经过了20 s以上的超调过程；SMGSC则能非常好地稳定整个变形飞行过程，始终保持速度和高度的恒定。同时注意到在机翼伸展完成后，油门输出降低了约50%，这表明伸缩翼飞机能通过机翼变形以更小的燃油消耗实现同样的飞行状态，这正是可变形飞行器区别于常规飞行器的优势体现。

3.2.2 有复合干扰情况

在加入复合干扰的机翼收缩过程中，最优控制器和切换变增益控制器下的伸缩翼飞机都产生了明显振荡，而SMGSC仍能很好地保持飞行速度与高度的稳定，几乎没有任何波动，迎角、俯仰角等的变化也更为平稳，极大地提高了伸缩翼飞机的鲁棒性能。

图7给出了SMGSC对复合干扰的部分观测曲线，其中DV，Dq分别表示速度通道和俯仰角速度通道的复合干扰，可见观测值与实际值高度一致，表明了SMGSC对干扰观测的有效性，同时也验证了SMGSC对复合干扰的强鲁棒性。

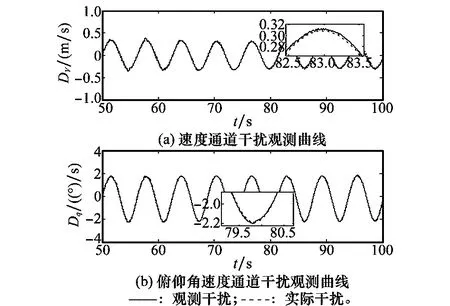
图7 滑模变增益控制器复合干扰观测曲线

4 结 论

本文根据伸缩翼飞机的Datcom气动特性仿真数据，构建了气动参数关于机翼变形状态的函数关系，进而建立了伸缩翼飞机在变形飞行过程中的非线性模型及LPV模型，在此基础上结合滑模观测理念提出了一种新的SMGSC方法，设计了相应的飞行控制器，进行了变形飞行的数值仿真对比实验，得到了以下结论：

（1）伸缩翼飞机的气动特性受机翼变形的直接影响，飞机运动模态也因此发生改变，这是机翼伸缩能够调节飞机性能的本质机理。

（2）提出的SMGSC策略避免了一般变增益控制对于网格划分与控制插值的不确定性，能从理论上保证系统在整个变参空间的全局稳定，并通过对复合干扰的观测估计提供极强的鲁棒控制能力。

（3）在SMGSC的控制下，伸缩翼飞机能在机翼伸缩的同时更好地保持期望的飞行状态，消除复合干扰的影响，提高飞行稳定性和鲁棒性；同时可以减少50%的燃油消耗实现同样的飞行任务，体现了可变形飞行器的性能优势。

［1］Barbarino S，Bilgen O，Ajaj R M，et al.A review of morphing aircraft［J］.Journal of Intelligent Material Systems and Structures，2011，22（9）：823- 877.

［2］Kudva J N.Overview of the DARPA smart wing project［J］.Journal of Intelligent Material Systems and Structures，2004，15（4）：261- 267.

［3］Rodriguez A R.Morphing aircraft technology survey［R］.Reston：American Institute of Aeronautics and Astronautics，2007.

［4］Bowman J，Sanders B，Cannon B，et al.Development of next generation morphing aircraft structures［R］.Reston：American Institute of Aeronautics and Astronautics，2007.

［5］Jouannet C，Lundström D，Amadori K，et al.Morphing wing design，from study to flight test［R］.Reston：American Institute of Aeronautics and Astronautics，2009.

［6］Matteo N D，Guo S，Ahmed S，et al.Design and analysis of a morphing flap structure for high lift wing［R］.Reston：American Institute of Aeronautics and Astronautics，2010.

［7］Wang Q，Chen Y，Tang H.Mechanism design for aircraft morphing wing［R］.Reston：American Institute of Aeronautics and Astronautics，2012.

［8］Wu J，Lu Y P.A distributed coordinated control scheme for morphing wings with sampled communication［J］.Chinese Journal of Aeronautics，2010，23（3）：364- 369.

［9］Yin M，Lu Y P，He Z，et al.Modeling and sliding mode control of morphing aircraft for morphing-aided maneuver［J］.Systems Engineering and Electronics，2015，37（1）：128- 134.（殷明，陆宇平，何真，等.变体飞行器变形辅助机动的建模与滑模控制［J］.系统工程与电子技术，2015，37（1）：128- 134.）

［10］Apkarian P，Gahinet P，Becker G.Self-scheduled H∞control of linear parameter-varying systems：a design example［J］.Automatica，1995，31（9）：1251- 1261.

［11］Chen J F，Liu K.Gain-scheduled robust controller design for AMB-rotor system based on LMI［J］.Journal of National University of Defense Technology，2011，33（6）：134- 138，144.（陈峻峰，刘昆.基于LMI的磁轴承 转子系统鲁棒增益调度控制器设计［J］.国防科技大学学报，2011，33（6）：134- 138，144.）

［12］Wu C F，Shao P Y，Ma S H.An effective design of LPV based robust gain-scheduling controller for morphing-wing UAV［C］∥Proc.of the 32nd Chinese Control Conference，2013：2655- 2660.

［13］Wang T，Wang Q，Jiang W L，et al.Gain scheduled control of morphing vehicle based on switched polytopic system［J］.Journal of Beijing University of Aeronautics and Astronautics，2014，40（1）：75- 79.（王通，王青，江未来，等.基于切换多胞模型的变体飞行器增益调参控制［J］.北京航空航天大学学报，2014，40（1）：75- 79.）

［14］Abdulrahim M，Lind R.Control and simulation of a multi-role morphing micro air vehicle［R］.Reston：American Institute of Aeronautics and Astronautics，2005.

［15］Gandhi N，Cooper J，Ward D，et al.A hardware demonstration of an integrated adaptive wing shape and flight control law for morphing aircraft［R］.Reston：American Institute of Aeronautics and Astronautics，2009.

［16］Valasek J，Lampton A，Marwaha M.Morphing unmanned air vehicle intelligent shape and flight control［R］.Reston：American Institute of Aeronautics and Astronautics，2009.

［17］Xu C，Lu Y P，Liu Y B，et al.Dynamic modeling and sliding mode control of multi-moving-body spacecraft using screw theory［J］.Systems Engineering and Electronics，2012，34（12）：2535- 2540.（许晨，陆宇平，刘燕斌，等.多运动体航天器旋量理论动力学建模与滑模控制［J］.系统工程与电子技术，2012，34（12）：2535- 2540.）

［18］Cheng L，Jiang C S，Du Y L，et al.The sliding mode disturbance compensated GPC method for a class of uncertain systems［J］.Control Theory&Applications，2010，27（2）：175- 180.（程路，姜长生，都延丽，等.一类不确定系统基于滑模干扰补偿的广义预测控制［J］.控制理论与应用，2010，27（2）：175- 180.）

［19］Zhang R M，Sun C Y，Zhang J M，et al.Second-order terminalsliding mode control for hypersonic vehicle in cruising flight with sliding mode disturbance observer［J］.Journal of Control Theory and Applications，2013，11（2）：299- 305.

［20］Ren Y，Liu Z H，Zhou R.Applications of low speed opto-electronic tracking systems based on sliding mode disturbance observer［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39（6）：835- 840.（任彦，刘正华，周锐.滑模干扰观测器在低速光电跟踪系统中的应用［J］.北京航空航天大学学报，2013，39（6）：835- 840.）

［21］Marcos A，Balas G J.Development of linear-parameter-varying models for aircraft［J］.Journal of Guidance，Control，and Dynamics，2004，27（2）：218- 228.

［22］Shtessel Y B，Moreno J A，Plestan F，et al.Super-twisting adaptive sliding mode control：a Lyapunov design［C］∥Proc.of the IEEE 49th Conference on Decision and Control，2010：5109- 5113.

［23］Wu K，Fan J S，Zhang H X，et al.A new disturbance observer design based on higher-order sliding mode control［J］.Journal of Projectiles，Rockets，Missilesand Guidance，2012，32（4）：199-202.（吴坤，范金锁，张合新，等.基于高阶滑模的新型干扰观测器设计［J］.弹箭与制导学报，2012，32（4）：199- 202.）

［24］Levant A.Universal single-input-single-output（SISO）slidingmode controllers with finite-time convergence［J］.IEEE Trans.on Automatic Control，2001，46（9）：1447- 1451.

［25］Hall C E，Shtessel Y B.Sliding mode disturbance observerbased control for a reusable launch vehicle［J］.Journal of Guidance，Control，and Dynamics，2006，29（6）：1315- 1328.

殷 明（198-5- ），男，博士研究生，主要研究方向为先进飞行器建模与控制。

E-mail：dragonyinming＠nuaa.edu.cn

陆宇平（195-7- ），男，教授，博士研究生导师，主要研究方向为智能变形体控制技术、高超声速飞行精确控制。

E-mail：yplac＠nuaa.edu.cn

姚克明（197-8- ），男，讲师，博士后，主要研究方向为复杂多体系统协调控制、飞行器控制与自主导航。

E-mail：ykm_1997＠163.com

何 真（198-1- ），女，副教授，博士，主要研究方向为先进飞行控制、复杂系统建模与控制。

E-mail：hezhen＠nuaa.edu.cn

Modeling and sliding mode gain-scheduled control for telescopic-wing aircraft in flight during morphing

YIN Ming1，LU Yu-ping1，YAO Ke-ming1，2，HE Zhen1
（1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.College of Electric and Information Engineering，Jiangsu University of Technology，Changzhou 213001，China）

To analyze the effect of wing deformation on the aircraft performance，and realize steady flight of the aircraft during morphing，the dynamic modeling and the robust control for the telescopic-wing aircraft in flight during morphing are studied.First，the aerodynamic parameters of the telescopic-wing aircraft are established as functions of wing deformation via simulation and analysis.The dynamic models of the telescopic-wing aircraft in flight during morphing are constructed subsequently.Then，a novel sliding mode gain-scheduled control（SMGSC）strategy is proposed to guarantee the global stability and robustness of the closed-loop plant.The simulation results show that，the aerodynamic performance and the motion modes of the telescopic-wing aircraft can be affected by the wing deformation.The proposed SMGSC can provide a higher stability and a stronger disturbance rejection for the telescopic-wing aircraft in flight during morphing.The telescopic-wing aircraft can perform the same flight task with 50%less fuel consumption through wing deformation，which means a great advantage over conventional aircraft.

telescopic-wing aircraft；flight during morphing；dynamic modeling；sliding mode gain-scheduled control（SMGSC）；fuel consumption

V 249.1

A

10.3969／j.issn.1001-506X.2015.11.20

1001-506X（2015）11-2554-07

2014- 12- 25；

2015- 02- 27；网络优先出版日期：2015- 04- 28。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150428.1653.004.html

国家自然科学基金（91016017，61304139）；江苏省自然科学基金（BK20130234，BK20130806）；江苏省高校自然科学基金（13KJD510003）资助课题