基于多变量决策树交通事件持续时间预测模型

向红艳，金 明

(1. 重庆交通大学 交通运输学院，重庆 400074；2. 重庆工业职业技术学院 车辆工程学院，重庆 401120)



基于多变量决策树交通事件持续时间预测模型

向红艳1，金 明2

(1. 重庆交通大学 交通运输学院，重庆 400074；2. 重庆工业职业技术学院 车辆工程学院，重庆 401120)

基于粗集理论和决策树方法，建立了交通事件持续时间的多变量决策树预测模型。通过分析交通事件的属性特点，运用粗集理论中的属性约简方法，确定了交通事件的核心属性；运用等价关系相对泛化原理构造了多变量组合检验，并根据变量依赖度确定了最优变量组合；以多变量组合判据代替单变量判据建立了决策树模型，利用决策树高度和节点样本数对树的规模进行控制，优化了决策树结构。实例应用表明，该模型对交通事件持续时间的分类和预测能力较强，预测精度较高。

交通工程；持续时间；粗糙集；多变量决策树；预测

0 引 言

高速公路交通事件管理是高速公路日常运营管理与控制的重要组成部分。随着我国高速公路运营里程的迅猛增长，各种原因导致的高速公路交通事件数量日益增多。高速公路交通事件造成的人员伤亡和经济损失巨大，其社会影响十分显著。高速公路交通事件主要包括交通事故、自然灾害以及其他突发事件等。交通事件的持续时间是高速公路管理部门和道路使用者十分关注的指标，是实施交通事件管理和应急救援的重要依据。持续时间预测结果有利于帮助高速公路管理者快速制定决策以减轻交通事件造成的拥堵、出行延误，减少二次事故发生率，降低人员伤亡和财产损失。

关于交通事件持续时间的预测方法主要有：回归分析法[1-2]，概率分布法[3-5]，单变量决策树法[6-7]。交通事件持续时间的影响因素主要包括交通事件类型、发生时间、地点、占道、人员伤亡、车辆、环境、救援、天气等，由于上述影响因素相互作用及耦合关系十分复杂，造成现有方法的预测精度十分有限。因此，决策树方法是数据挖掘中应用最广泛的方法之一。

决策树采用优先策略自上而下进行不断细分和输出预测结果。刘伟铭，等[6]建立了不同类别交通事件的单变量决策树模型，提出了基于单因素显著性判据的节点分类判别方法，分别预测了火灾、故障、人员伤亡等类别交通事件的持续时间；C．Zhan，等[7]提出了基于M5P方法的单变量决策树模型，该方法通过整合决策树法与回归分析法，采用不同分类情况下多个多元线性回归模型计算交通事件的持续时间，提高了预测精度，其结果优于简单决策树模型。然而，上述模型均以单以变量作为决策判据建立模型，导致所建立的决策树判别规则十分复杂，容易造成树形庞大，计算效率低。同时，单变量决策树忽略了要素之间的相关性，还有可能造成变量的重复检验，影响预测效果。基于此，笔者结合粗集理论中的属性约简和等价关系泛化原理，建立基于粗糙集的多变量决策树预测模型，以改进交通事件持续时间的预测效果。

1 交通事件的持续时间特征

1.1 持续时间的定义

交通事件持续时间可以分为4个阶段：①报警时间，是指从交通事件发生到管理人员接到报警的时间；②响应时间，是指接到报警开始一直到救援队伍到达现场之间经历的时间；③现场处理时间，是指救援队伍现场抢救伤员，清理障碍的时间；④恢复交通事件，是指从现场清理完毕到交通完全恢复正常的时间。

但现有资料大多数无法统计高速公路交通事件发生后到报警前的这一段时间，现场清理完成到交通状态恢复正常的时间也无法准确统计。因此，笔者将研究的高速公路交通事件持续时间确定为：以高速公路管理部门接到报警为开始时间，以交通事件现场处理完毕工作人员全部撤离为结束时间。这一时间主要包括响应时间和现场处理时间，不包括报警时间和恢复交通事件，交通事件持续时间与事件类别、严重程度、发送地点、发生时间有关。交通事件的持续过程见图1。

图1 交通事件的持续过程

1.2 交通事件持续时间的特征

根据我国高速公路交通事故的统计资料进行分析，结果表明：高速公路交通事件的持续时间分布具有一定的规律性。其中持续时间短(<30 min)的交通事件占绝大多数，随着持续时间增长，交通事件数量呈现逐渐减少的趋势。根据K．Ozbay，等[8]的研究，交通事件的持续时间总体上近似服从对数正态分布，具有向左偏移的特征。不同类别的交通事件持续时间具有不同的均值和变异系数，其变化特征差异较大；同一类别相同严重程度的交通事件，其持续时间总体上服从呈正态分布[6]。交通事件的持续时间的影响因素十分复杂，不仅与交通事件本身的性质有关，还与救援实施的进度有关，准确预测交通事件持续时间，有助于缓解交通事件造成的出行延误、交通拥堵等问题。

2 基于粗集的多变量决策树模型

粗集理论具有处理模糊性、不确定和不完整数据的强大能力[9-11]。笔者尝试建立一种基于粗集理论与决策树算法整合的多变量组合预测模型。其具体方法为：在传统方法基础上，运用粗集中的属性约简方法，构造决策变量相对核；在建立决策树过程中，允许两个或多个属性变量的组合检验，根据等价关系泛化原理，产生更快速、有效的决策判据；通过限制节点记录数和树的最大高度，对决策树的结构进行修剪和优化。多变量决策树的优点在于考虑了变量之间的相关性，通过变量组合降低了算法的复杂性，减小了树的规模，提高了计算速度。

2.1 交通事件属性变量的约简

设交通事件样本集合为U，x表示任意交通事件样本，x∈U。设表示描述交通事件的属性集合为R={R1，R2，…，Rn}。为消除属性集合中不必要的冗余属性，运用属性约简算法构造属性变量相对核。

对任意属性Ri，设U/Ri为根据Ri的取值对U进行的一个划分，将序对(U，Ri)称为一个近似空间。设[x]Ri为包含x的Ri的等价类，对任意集合X∈U，定义以Ri为基础的集合X的上、下近似集合为：

(1)

设T表示决策属性(即持续时间)，U/T表示根据决策变量T的取值对U进行的划分。令P表示约简后的核心属性集，则P的T正区域为：

(2)

式中：IND(P)，IND(T)分别表示P，T中元素的交集。对集合R中的元素进行逐一检验，如果：

POSIND(P)[IND(T)]=POSIND(P-Ri)[IND(T)]

则Ri为不必要的属性，予以剔除。取R中剩下元素得到交通事件属性相对核P：

P=∪{Ri∈R:POSIND(P)[IND(T)]≠

POSIND(P-Ri)[IND(T)]}

(3)

2.2 构建多变量组合检验

设交通事件的持续时间用T表示，T为决策属性。按照T的取值将持续时间分为h级，T={T1，T2，…，Th}。根据T对U进行划分：U/T={Yt}，t=1,2，…，h；满足T(Yt)=Tt。从P中选择任意k个变量，利用等价关系相对泛化原理建立多变量组合检验C，见式(4)。

C=P1∧P2∧…∧Pk，(k=1，2，…，m)

(4)

以C对U进行新的划分，得：

U/IND(C)={X1，X2，…，Xr}

(5)

令Z={Z1，Z2，…，Zh，Z(h+1)}，对任意Xj∈U/IND(C) (j=1，2，…，r)进行检验，判断其是否属于U/T中的元素；若Xj⊆Yt(t=1，2，…，h)，将Xj的元素归入Zt，将不属于任何U/T子集的元素一起归入集合Z(h+1)。Z即为根据变量组合C在U上确定的新的等价关系，是C相对于T的泛化。如式(6)、式(7)：

Zt=∪Xj∈U/IND(C){Xi;Xj∈Yt}，(t=1，2，…，h)

(6)

Z(h+1)=∪Xj∈U/IND(C){Xi;Xj∉Yt,∀t}

(7)

选择依赖度最大的变量组合作为最优组合，记为C*，见式(8)：

Card[POSCq(T)]/Card(U)，(q=1,2,…)

(8)

式中：γ(Cq,T)表示决策属性T对变量组合Cq的依赖度；Card(U)表示集合U中的元素个数。

2.3 建立多变量持续时间决策树

令N表示决策树的节点；UN表示节点上的当前交通事件样本集合；lN表示交通事件样本个数。在建树过程中通过限制树的最大高度和每个节点的最少样本数来控制树的生长。令树的最大高度为Nmax，节点必须包含的最少记录数为lmin。以下是构建多变量决策树的具体步骤。

1)创建决策树根节点，N=1；

2)根据式(1)～式(3)对节点N上的当前样本集合UN进行属性约简，得到属性相对核PN；

3)采用式(4)、式(5)构造节点N的最优多变量检验CN*。

4)用式(6)、式(7)计算等价关系Z，并为节点UN分配类别，共有(h+1)类；

5)分别计算子集Zi(i=1,2,…,h)所对应的持续时间；

6)判断是否满足条件：Nlmin，如果满足，至7)，否则，至8)；

7)令N=N+1，UN=Z(h+1)，回2)；

8)结束，计算集合Z(h+1)所对应的持续时间。

其中，当决策树叶节点上的交通事件集合为Zt时，对应的持续时间预测结果为Tt,t=1，2，…，h。当决策树叶节点上的交通事件集合为Z(h+1)时，按照T的等级对Z(h+1)进行划分，选择Z(h+1)/T中元素最多的子集所对应的持续时间作为预测结果，具体见式(9)：

(9)

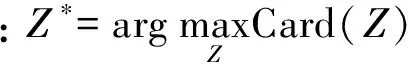
3 实例应用

采用某双向4车道高速公路2012年全年的交通事件数据进行应用分析。所用数据来源于高速公路管理部门交通事件统计报表以及部分文本整理资料。案例包含有效组样本数据833组，平均延误时间为53 min，样本数据80%用于决策树构造， 20%用于预测效果验证。

对描述交通事件的变量进行赋值和离散化处理。将持续时间T将分为5个等级，即：T={A，B，C，D，E}。其中：A(T≤30 min)，B(30 min300 min)，具体见表1。

表1 交通事件属性描述及赋值

注：表中未列出交通事件的非核心属性，包括：所属公司、路段名称、行车方向、车道数、涉及车辆总数、车型、聚众人数、处置措施、二次事故、特殊路段等。

运用式(1)～式(3)对交通事件初始属性集进行约简，得到属性相对核：P= (P1，P2，…，P11)，见表1。令决策树最大高度Nmax=10，节点样本数最小值lmin=15，节点多变量组合数k≤3。建立多变量决策树如图2，图2中，椭圆形表示决策节点，括号内的数字表示当前训练样本数，长方形表示叶节点，括号内字母表示叶节点对应的持续时间等级，括号内的数字表示该叶节上的交通事件样本数。

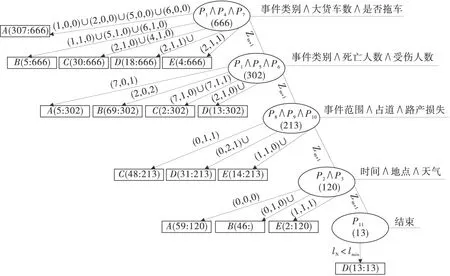
图2 多变量决策树结构

为评价模型的预测效果，选用预测准确率和误报率作为评价指标。其中，预测准确率为模型可准确预测持续实际范围的交通事件数与交通事件总数之比，误报率为未能准确预测的交通事件数与事件总数之比，具体见式(10)、式(11)：

(10)

σ=1-μ

(11)

式中：μ为预测准确率；σ为误报率；S为用于测试的交通事件总数；Sa为叶节点a上预测准确的交通事件数；w为叶节点总数。

运用构造的决策树对验证数据进行预测，按照持续时间等级对测试数据进行分组，各组验证样本的预测结果见表2。

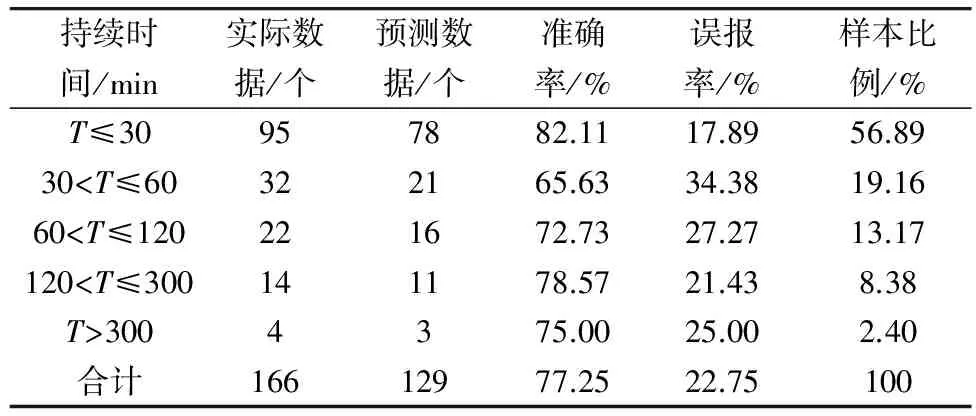
表2 预测结果分析

表2的结果表明：多变量决策树通过对核心属性的组合，有利于快速分类和分级，预测平均准确率为77.25%。其中：对T≤30 min的交通事件预测准确率大于80%；对持续时间较长(120 min300 min)的交通事件预测准确率大于75%。由于持续时间本身具有随机性，在更小时间范围上的精确预测变得十分困难，持续时间30 min

与H．L．Chang，等[12]的预测效果相比较，结果见表3。由表3可见，与单变量决策树比较，多变量决策树的高度降低28.57%，叶节点数量减少40.74%，因此加快了交通事件的分类和分级运算速度。

表3 单变量、多变量决策树的比较

4 结 语

利用粗糙集理论中的属性约简法和多变量构造检验方法，建立了具有较强分类和预测能力的多变量决策树模型。该模型可有效避免交通事件初始属性集合中冗余属性的干扰，所建立的决策树规模、结构更加合理。研究中发现交通事件持续时间的核心影响因素包括交通事件类别、是否涉及大货车、车辆是否损坏、人员伤亡、占道、路产损失、地点、时间、天气。交通事件的持续时间的变化范围较大，多变量决策树能真实反应交通事件持续时间的变化特征，可快速识别持续时间短、较短、中、长、较长的不同类别交通事件，具有较高的预测精度。由于样本数量和描述交通事件的指标有限，笔者尚未结合区域社会经济、交通管理水平对不同地区交通事件的持续时间进行分析，下一步将考虑上述因素的影响对这一问题进行研究。

[1] Garib A,Radwan A E,Al-Deek H.Estimating magnitude and duration of incident delays [J].Journal of Transportation Engineering,1997,123(6):459-466.

[2] Smith K W,Smith B L.Forecasting the Clearance Time of Freeway Accidents[D].Virginia:University of Virginia,2001.

[3] Nam D,Mannering F.An exploratory hazard-based analysis of highway incident duration[J].Transportation Research Part A:Policy and Practice,2000,34(2):85-102.

[4] Hojati A T,Ferreira L,Washington S,et al.Hazard based models for freeway traffic incident duration[J].Accident Analysis & Prevention,2013,52:171-181.

[5] 康国祥,方守恩.基于风险分析的交通事件持续时间预测[J].同济大学学报:自然科学版,2012,40(2):241-245. Kang Guoxiang,Fang Shouen.A hazard-based analysis of traffic incident duration prediction[J].Journal of Tongji University:Natural Science,2012,40(2):241-245.

[6] 刘伟铭,管丽萍,尹湘源.基于决策树的高速公路事件持续时间预测[J].中国公路学报,2005,18(1):99-103. Liu Weiming,Guan Liping,Yin Xiangyuan.Prediction of freeway incident duration based on decision tree[J].China Journal of Highway and Transport,2005,18(1):99-103.

[7] Zhan C,Gan A,Hadi M.Prediction of lane clearance time of freeway incidents using the M5P tree algorithm[J].Intelligent Transportation Systems,IEEE Transactions on,2011,12(4):1549-1557.

[8] Ozbay K,Kachroo P.Incident Management in Intelligent Transportation Systems [M].Boston,MA:Artech House,1999.

[9] 苗夺谦,王珏.基于粗糙集的多变量决策树的构造方法[J].软件学报,1997,8(6):425-431. Miao Duoqian,Wang Jue.Rough sets based approach from multivariate decision tree construction[J].Journal of Software,1997,8(6):425-431.

[10] 童世鑫,丛浩哲,陈雨人.高速公路交通事件清除时间模糊逻辑预测模型[J].重庆交通大学学报:自然科学版,2011,30(1):85-88. Tong Shixin,Cong Haozhe,Chen Yuren.Fuzzy logic prediction model for clearance time of freeway traffic incidents[J].Journal of Chongqing Jiaotong University:Natural Science,2011,30(1):85-88.

[11] 孙连超,邵毅明,颜雪丽,等.基于TCT的公路交通事故黑点鉴别方法研究[J].重庆交通大学学报:自然科学版,2012,31(1):63-67. Sun Lianchao,Shao Yiming,Yan Xueli,et al.Identification of highway traffic accident black-spots based on traffic conflict technique [J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(1):63-67.

[12] Chang H L,Chang T P.Prediction of Freeway Incident Duration based on Classification Tree Analysis[J].Journal of the Eastern Asia Society for Transportation Studies,2013,10:1964-1977.

A Traffic Incident Duration Time Predication Model Using Multivariable Decision Tree

Xiang Hongyan1, Jin Ming2

(1. School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074, China; 2. School of Automotive Engineering, Chongqing Industry Polytechnic College, Chongqing 401120, China)

Using theory and method of rough set and decision tree, a multivariable decision tree model was developed for traffic incident duration time prediction. Through analyzing the incident attributes, the attribute reduction algorithm in rough set theory was used to get the core attributes of the incident. By using the generalization principle of equivalence relation, a multivariable combination test was formed. By comparing the dependence of different variable combinations, the optimal variable combination was determined. Then, multivariable combination criterion instead of single variable criterion was used to set up the decision tree, and through limiting tree height and number of tree leaves, the scale of tree was controlled, so, the tree’s structure was optimized. The case study shows that this model has a good performance in classifying and forecasting traffic incident duration time, and it has good accuracy in duration time forecasting.

traffic engineering; duration; rough set; multivariable decision tree; predication

10.3969/j.issn.1674-0696.2015.03.23

2014-07-01；

2014-09-22

向红艳(1980—)，女，湖北恩施人，副教授，博士，主要从事交通运输规划与管理方面的研究。E-mail: xiang-@126.com。

U491.1

A

1674-0696(2015)03-112-05