无信号交叉口交通冲突分析

张 邻，黄选伟，吴伟明

(南昌航空大学 数学与信息科学学院，江西 南昌 330063)



无信号交叉口交通冲突分析

张 邻，黄选伟，吴伟明

(南昌航空大学 数学与信息科学学院，江西 南昌 330063)

为了研究无信号交叉口冲突车辆间驾驶员的决策行为，从博弈角度出发，根据影响驾驶员决策行为的性格因素，以及不同策略之间相对的势因素，通过时间细化，建立基于重复博弈下影响驾驶员决策行为的效用函数。通过驾驶员在交叉行进过程中的决策行为，分析不同驾驶员决策行为组合的效用，确定博弈过程中存在Nash均衡，得到动态博弈中驾驶员的最优决策。例证表明：冲动型的驾驶员在各决策时间段内更愿意选择加速抢先策略；温和型的驾驶员在各决策时间段内偏好于加速抢先策略或保持匀速策略；谨慎型的驾驶员在各决策时间段内偏好于选择保持匀速策略或减速礼让策略。

交通工程；无信号交叉口；重复博弈；交通冲突；Nash均衡

0 引 言

无信号交叉口在整个交通网络中起着举足轻重的作用，如果运行不良则会影响整个交通系统的运行。由于没有信号灯控制，驾驶员的主观决策行为，直接影响着无信号交叉口的运行情况，驾驶员必须自己判断进入交叉口的安全时刻，寻求在交通流中进入交叉口的安全机会，使车辆安全、快速地通过交叉口。因此，深入研究无信号交叉口驾驶员的决策行为可以改善无信号交叉口的通行效率、减少无信号交叉口交通事故，同时也为分析无信号交叉口车辆间的相互冲突提供理论支持，所以，对于无信号交叉口驾驶员决策行为的研究具有非常重要的现实意义。

许多学者对驾驶员决策行为进行研究[1-4]。Mutat Demir，等[5]提出了一种驾驶模拟器为不同性格的驾驶员提供模拟驾驶环境，建立了驾驶员的行为模型，这能让驾驶员在一个安全的环境中练习驾驶，减少交通事故的发生，但是其没有结合驾驶员的行为模型来评估驾驶模拟器的有效性，且驾驶模拟和现实的交通环境还存在很大差别；Chen Chang-kuna，等[6]运用元胞自动机模型对T型交叉口行人的疏散行为进行研究，结果表明行人密度对交叉口行人的疏散行为影响较大，但只是对信号交叉口行人的疏散行为进行了研究，没有考虑无信号交叉口机动车与机动车之间无序的冲突互动。王晓原,等[7]运用冲突点法进行驾驶员的决策行为仿真，深入分析多源信息刺激下驾驶员协同行为；陈富坚,等[8]运用博弈论知识建立交叉口驾驶员的决策行为模型，通过混合策略的Nash均衡解，引入信号灯轮换均衡机制的设置标准；郭伟,等[9]利用场图工具建立了交叉口驾驶员行为模型，并设计了基于博弈论的协调算法。这些模型将冲突车辆间驾驶员的决策行为均简化为“单次决策”，不能准确的刻画交叉口冲突车辆间驾驶员复杂的心理过程，忽略了冲突车辆间驾驶员决策行为的相互影响。刘小明,等[10]从更小时空尺度考虑无信号交叉口驾驶员插车行为，并建立了基于博弈论[11-12]的无信号交叉口驾驶员插车行为模型,分析了不同驾驶员类型组合在插车博弈过程中的Nash均衡，及相应的驾驶员行为，但是其交通冲突时间的界定指标选取为定值，而此值应与冲突车辆的速度有关。上述这些模型从微观角度，合理的刻画交通状态演化或交通控制效果，但这些模型没有考虑驾驶员决策时空尺度，没有考虑不同性格类型驾驶员在不同冲突位置的决策行为差异，适用性不强。

基于上述原因，笔者根据博弈论知识以及驾驶员的性格和心理特征，对无信号交叉口驾驶员决策行为进行多时段分析，考虑不同类型驾驶员决策行为的差异，并结合冲突车辆到冲突点的距离因素，建立了基于动态重复博弈的驾驶员决策行为模型，通过实例，应用模型模拟驾驶员的最优决策行为。

1 无信号交叉口机动车辆间博弈分析

无信号交叉口的车、自行车和人的通行，是车、自行车和人的相互博弈过程，其中，机动车与机动车的博弈是典型的“重复博弈”的过程，驾驶员为了尽快地通过冲突区域进行一系列的决策，该过程是完全信息下的动态博弈过程。

图1为一双向2车道无信号交叉口，N代表北，S代表南，W代表西，E代表东。对于直行车流，在交叉口冲突区内有4个冲突点A，B，C，D，其中，A为N→S与W→E两直行车流的冲突点；B为S→N与W→E两直行车流的冲突点；C为S→N与E→W两直行车流的冲突点；D为N→S与E→W两直行车流的冲突点；L1为n1到A点的距离；L2为n2到A点的距离；L为冲突区域的半径(常数)，这里的冲突区域指的是以冲突点为圆心，以机动车间相互产生影响的临界距离为半径的圆[7]，可简单表示为：

(1)

式中：vm为由于道路条件限制，车辆所能达到的最大速度；t为驾驶员的反应时间，一般取为0.5s；am为车辆的最大减速度；w为机动车间的安全距离，一般取为2m。

正常情况下，机动车的加速度a=2.5m/s2，紧急情况下a=7.3m/s2[7]，这里取am=7m/s2，令vm=60km/h，根据式(1)，得L=30m。

图1 无信号交叉口示意

假设此时交叉口无视野遮挡，N→S方向有1个车辆n1，W→E方向有1个车辆n2，假设n1的驾驶员发现n2时，n1到A点的距离为d1，n2到A点的距离为d2，且此时n1与n2的速度分别为v1和v2，加速度分别为a1和a2。

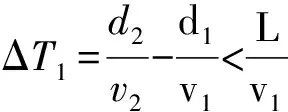
(2)

式中：Δt为每一时段的时间长度。

(3)

(4)

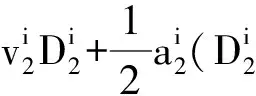
(5)

同理可得:

(6)

(7)

(8)

(9)

因此，n1与n2到达冲突点A的时间差ΔTi为：

(10)

2 机动车间博弈模型的建立

重复博弈是指同样结构的博弈重复多次，在重复博弈中，所有参与人都能观测到博弈过去的历史，并且所有参与人都是同时采取行动。令无信号交叉口冲突区域的参与人l博弈的策略空间为：

n1与n2两个参与人重复博弈过程中，他们的效用不仅与自己的策略有关，还和对方的策略有关，因此，n1与n2的效用函数可分别表示为：

在车辆通过无信号交叉口的过程中，驾驶员均希望能安全尽快地通过交叉口，其中安全是首要因素。因此，可以从安全这一方面来衡量效用。

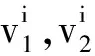
(11)

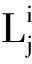
若n1先到达冲突点A：

(12)

若n2先到达冲突点A：

(13)

式中：j=1,2;i=1,2,…，k;G[·]表示对计算结果的数据处理。

3 算 例

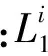
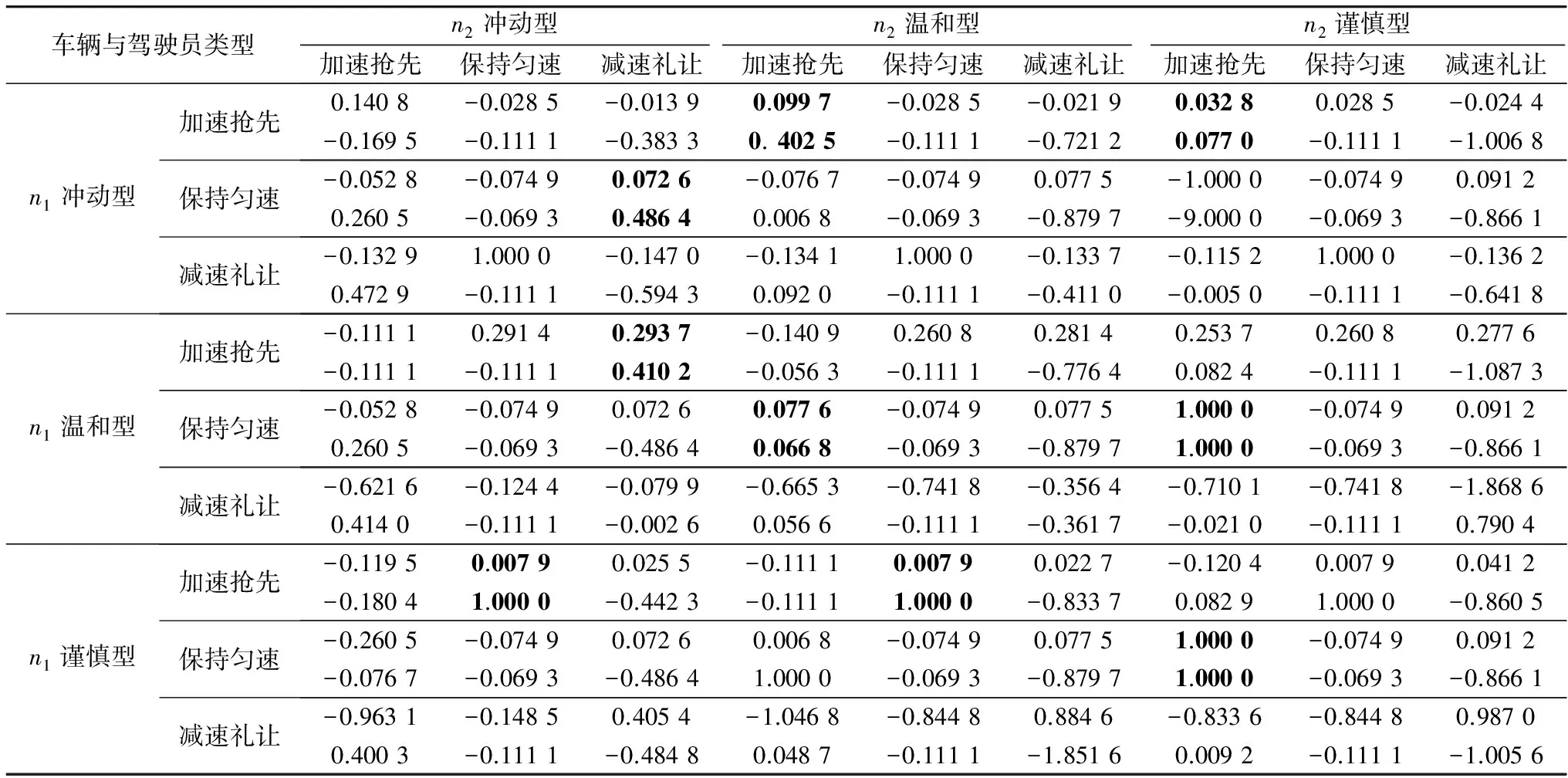
表1 博弈效用值

由表1知，在n1与n2的驾驶员博弈过程中，存在Nash均衡，如表中的加粗部分的数据就是双方采取各种策略对应的均衡效用。

表2是根据表1参与博弈双方获得的效用，得到双方对应的最优策略。如当n1与n2的驾驶员为(冲动型，温和型)时，n1与n2的驾驶员的最优策略为：n1的驾驶员选择加速抢先，n2的驾驶员选择加速抢先。

表2 博弈过程中不同驾驶员类型组合的最优策略

图2表示不同驾驶员性格类型及不同策略间n1与n2的效用值的变化趋势。

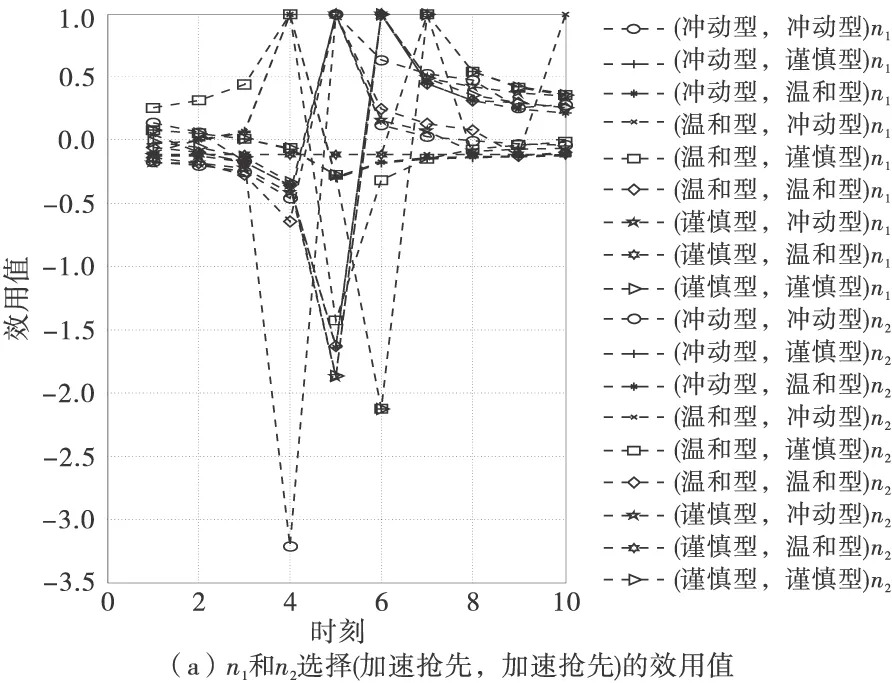
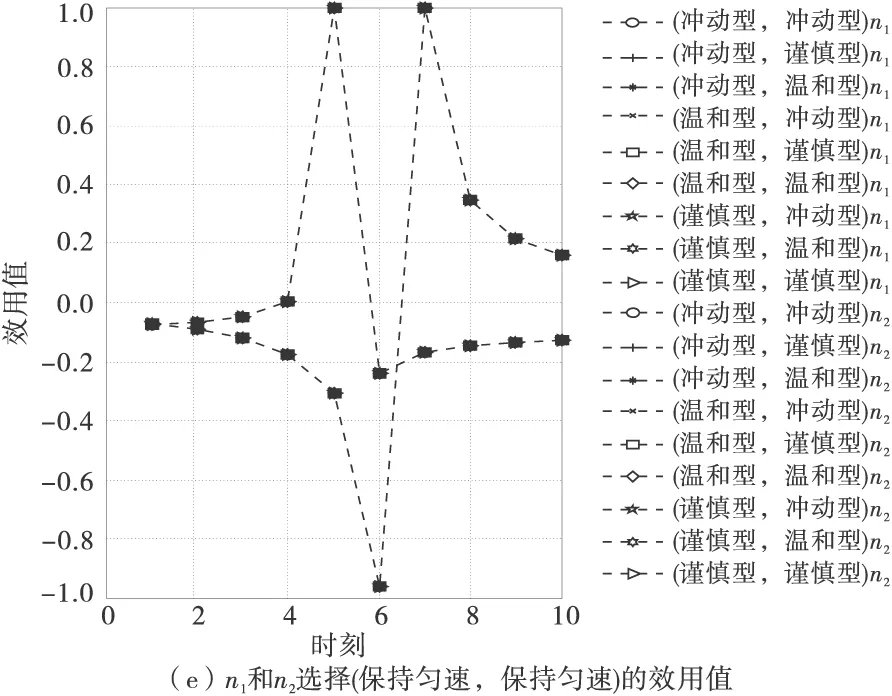
图2 不同驾驶员类型和策略下n1与n2的效用值

由图2可见：以n1与n2选择(加速抢先，加速抢先)策略为例，若n1与n2为(冲动型，冲动型)，在前3个时间段内，n1与n2的效用值呈下降趋势，且在时刻4达到下峰值，n1与n2之间存在交通冲突且交通冲突越来越严重，时刻4～时刻5，n1与n2的效用值呈上升趋势且到达上峰值，n1与n2之间的交通冲突逐渐得到缓解，时刻5～时刻9，n1与n2的效用值呈下降趋势，n1与n2之间不存在交通冲突但效用值在逐渐减小，时刻9之后n1与n2的效用值均在小范围内波动基本趋于稳定，n1与n2之间不存在交通冲突。在整个时间段内，n1的效用值变化在时刻4最为突出，改变行为策略的可能性较大，n2的效用值变化在时刻5最为突出，改变行为策略的可能性较大。

若n1与n2为(冲动型，谨慎型)，在前3个时间段内，n1的效用值呈上升趋势且到达上峰值，n2的效用值呈下降趋势，时刻4～时刻5，n1与n2的效用值均呈下降趋势且n1的效用值到达下峰值，时刻5～时刻6，n1的效用值呈上升趋势，n2的效用值呈下降趋势且到达下峰值，时刻6～时刻7，n1与n2的效用值均呈上升趋势且n2的效用值到达上峰值，时刻7之后n1与n2的效用值均在小范围内波动基本趋于稳定。在整个时间段内，n1的效用值变化在时刻4最为突出，改变行为策略的可能性较大，n2的效用值变化在时刻6最为突出，改变行为策略的可能性较大，同理分析知，若n1与n2为(冲动型，温和型)，n1与n2安全通过冲突点的可能性较大，所以n1与n2在博弈开始时可能选择(加速抢先，加速抢先)策略。

分析图2知，对于不同的驾驶员性格类型组合与不同的行为策略，n1与n2改变策略的时刻也各有差异，如冲动型的驾驶员选择(加速抢先，加速抢先)策略时，其改变行为策略集中在时刻4和时刻5，温和型的驾驶员选择(加速抢先，加速抢先)策略时，其改变行为策略集中在时刻5和时刻6，因此，不同的驾驶员性格类型组合，在不同的时刻的最优行为策略也有较大差异，对他们通过交叉路口时给出的建议也会有所不同。

对于(冲动型，冲动型)的驾驶员组合，为了确保安全的通过交叉路口，双方应尽量减慢车速，在每一个决策时间段内，通过对方的决策行为适时改变自己的决策，分析表明，在博弈开始的前几个决策时间段内，驾驶员双方选择(保持匀速，减速礼让)的可能性很大，在之后的几个决策时间段内选择(加速抢先，保持原速)，博弈过程即将结束的几个决策时间段内选择(加速抢先，减速礼让)安全通过交叉路口；对于(冲动型，温和型)的驾驶员组合，分析图2中驾驶员效用值变化趋势，双方在整个博弈过程中的决策行为与(冲动型，冲动型)的驾驶员组合的决策行为大致相同。

同理，根据不同的驾驶员性格类型组合在每个时刻的决策行为可以看出，冲动型的驾驶员在各决策时间段内选择加速抢先的可能性较大；温和型的驾驶员在各决策时间段内偏好选择加速抢先、保持匀速，谨慎型的驾驶员在各决策时间段内偏好选择保持匀速、减速礼让。通过模拟表明，模型能很好的反映冲突车辆间不同性格的驾驶员所做的决策。

4 结 语

根据车辆通过无信号交叉口过程中不同驾驶员间的决策行为相互作用关系，将车辆间的冲突时间分成若干个更小的时间段，分析驾驶员在每一时间段内的策略行为。在重复博弈下，分析影响驾驶员决策行为的性格因素，建立不同策略之间相对势因素的效用函数，从博弈角度探讨驾驶员在交叉行进过程中的决策行为，建立了基于动态重复博弈下无信号交叉口的驾驶员行为策略模型，通过分析不同驾驶员决策行为组合的效用，确定博弈过程中存在Nash均衡，得到动态博弈中驾驶员的最优决策行为。

笔者提出的模型能够在一定程度上反映不同条件下驾驶员行为的变化过程，为研究冲突车辆通过无信号交叉路口时驾驶员的决策行为提供了理论参考。另外，可以改善无信号交叉口的通行效率、减少无信号交叉口交通事故、减少交叉口的行车延误、提高整体交通安全水平，但在建模过程中只考虑2辆车的博弈过程，并且对影响模型的相关因素做了相应的简化，更为合理的多车博弈模型，以及应用实例的实证模拟需要将来进一步研究。

[1] Gheorghiu A,Havarneanu C.Driving behaviour of a sample of young Romanian drivers[J].Procedia-Social and Behavioral Sciences,2011,33(1):697-701.

[2] Casucci M,Marchitto M,Cacciabue P C.A numerical tool for reproducing driver behaviour:experiments and predictive simulations[J].Applied Ergonomics,2009,41(2):198-210.

[3] Vingilis E,Seeley J,Wiesenthal D L,et al.Street racing video games and risk-taking driving:an internet survey of automobile enthusiasts[J].Accident Analysis and Prevention,2013,50(1):1-7.

[4] Türker özkan,Timo Lajunen T,Joannes E l,et al.Cross-cultural differences in driving behaviors:a comparison of six countries[J].Transportation Research Part F:Psychology and Behavior,2006,9(3):227-242.

[5] Murat Demir,Abdullah Çavu.A new driver behavior model to create realistic urban traffic environment[J].Transportation Research Part F:Psychology and Behavior,2012,15(3):289-296.

[6] Chen Chang-Kuna,Li Jian,Zhang Dong.Study on evacuation behaviors at a T-shaped intersection by a force-driving cellular automata model[J].Physica A:Statistical Mechanics and its Applications,2012,391(7):2408-2420.

[7] 王晓原,邢丽.机非混行环境下驾驶员行为建模及仿真[J].中国公路学报,2009,22(2):98-104. Wang Xiaoyuan,Xing Li.Modeling and simulation for driving behavior in mix-traffic environment[J].China Journal of Highway and Transport,2009,22(2):98-104.

[8] 陈富坚,郭忠印,柳本民,等.基于博弈论的道路交叉口信号灯设置标准[J].同济大学学报:自然科学版,2011,39(6):830-836. Chen Fujian,Guo Zhongyin,Liu Benmin,et al.Game analysis of standards for setting traffic signal lights at road intersection[J].Journal of Tongji University:Natural Science,2011,39(6):830-836.

[9] 郭伟,杨明,王冰,等.基于博弈论的路口多车协作算法[J].华中科技大学学报:自然科学版,2011,39(增刊2):385-391. Guo Wei,Yang Ming,Wang Bing,et al.Game theory based cooperative driving algorithm for intersection[J].Journal of Huazhong University of Science and Technology:Natural Science 2011,39(Sup2):385-391.

[10] 刘小明,王秀英.基于重复博弈的无灯控交叉口驾驶员行为模型[J].中国公路学报,2011,24(4):94-100. Liu Xiaoming,Wang Xiuying.Vehicle-cross action model in intersection without traffic light based on reduplicate game[J].China Journal of Highway and Transport,2011,24(4):94-100.

[11] 张邻,杜文,向红艳.基于合同模式交通分配模型和求解算法[J].公路交通科技,2010,27(2):97-102. Zhang Lin,Du Wen,Xiang Hongyan.Traffic assignment model and solution algorithm in transportation network based on contract model[J].Journal of Highway and Transportation Research and Development,2010,27(2):97-102.

[12] 魏连雨,李壮.基于路网特征的高速公路计重收费费率确定[J].重庆交通大学学报:自然科学版,2014,33(6):122-126. Wei Lianyu,Li Zhuang.Determination of freeway weight toll rate based on network characteristics[J].Journal of Chongqing Jiaotong University:Natural Science,2014,33(6):122-126.

Analysis of Traffic Conflict in Non-Signalized Intersection

Zhang Lin, Huang Xuanwei, Wu Weiming

(College of Mathematics and Information Science, Nanchang Hang Kong University, Nanchang 330063, Jiangxi, China)

In order to study the driver’s decision-making behaviors of the conflict vehicles in non-signalized intersection, according to the driver’s personality factors and the relative potential factors in the different strategies which affect the driver to make decisions, as well as the time refinement, the utility function of the driver’s behaviors based on the dynamic reduplicate game theory was built up from the view of game theory. As the decision-making behavior by the driver in the process of cross-road, analyzing the different combination of the utility of the driver’s decision-making behavior, Nash equilibrium was existed in a single game process, and the driver’s optimal decision behaviors in a dynamic game was obtained. The illustration shows that impulse drivers in the decision-making period of time are more willing to choose to accelerate the first strategy; mild drivers prefer to choose accelerate the preemptive strategy or maintain uniform strategy; cautious drivers prefer to choose to maintain uniform strategy or deceleration comity strategy.

traffic engineering; non-signalized intersection; reduplicate game; traffic conflict; Nash equilibrium

10.3969/j.issn.1674-0696.2015.03.22

2013-12-28；

2014-02-27

国家自然科学基金项目(51368046，71161005)；江西省教育厅科学技术研究项目(GJJ11518)

张 邻(1973—)，男，安徽庐江人，副教授, 博士，主要从事交通规划方面的研究。E-mail:zagln0@163.com。

U491

A

1674-0696(2015)03-105-07