基于改进蚁群算法的高速公路疏散路径研究

李巧茹，张 倩，陈 亮，崔 宁

(1．河北工业大学 土木工程学院，天津 300401；2．河北省土木工程技术研究中心，天津 300401)



基于改进蚁群算法的高速公路疏散路径研究

李巧茹1，2，张 倩1，陈 亮1，2，崔 宁1

(1．河北工业大学 土木工程学院，天津 300401；2．河北省土木工程技术研究中心，天津 300401)

根据高速公路应急疏散的特点，在交通分配中应用改进蚁群算法模型。首先引入路段交通量和通行时间函数作为算法转移规则的一部分，从而在进行搜索时优先考虑容量大和通行时间较短的路径。其次通过实验分析蚁群算法参数对计算结果和收敛速度的影响，给出了最优的参数组合。最后将最优参数组合应用于改进蚁群算法中，并通过仿真实验将改进蚁群算法与基础蚁群算法的路径搜索结果进行对比。结果表明：采用最优参数组合的蚁群算法不但加快了搜索速度，而且优化了全局最优解，通过基于GIS的高速公路应急疏散系统进行路径分析，得到系统最优的可视化疏散路径。

交通工程；疏散路径；蚁群算法；参数分析

0 引 言

出行者在高速公路上进行应急疏散路径选择时，需要根据道路的实时信息进行疏散路线判断，采用动态路径分析模型，并且结合合理的路径搜索算法以最短时间进行路径信息分析。王旭，等[1]将蚁群算法应用于路径规划中，通过仿真实验比较蚁群算法和Dijksrta算法，发现蚁群算法可以较快地找到一条近似最优路径；刘勇[2]指出人工智能算法是模拟自然界中生物为优化其生存状态，而进行适应环境的无意识寻优行为的优化仿生算法，这类算法具有不确定性，或理解为伴有一定的随机性，这种不确定性体现在自然界生物的生理机制，在求解某些复杂问题时优于Floyd算法和Dijksrta算法等确定型算法；徐勋倩，等[3]将蚁群算法应用于动态交通网络的用户均衡配流问题，但对非平衡问题没有做相应研究；孙华灿，等[4]提出将基础蚁群算法引入容量限制模型中，将交通分配的确定性与用户出行的随机性融入路径的搜索过程，并通过实例证明其可行性。这些文献证明了蚁群算法进行路径分析时有较好的随机性、适用于大规模网络，并且对于相同规模的网络其比传统路径算法用时短。

传统蚁群算法在求解路径优化问题中存在收敛速度慢、容易陷入局部最优路径等不足，然而由于蚁群算法具有正反馈、分布式计算等优势，其参数组合问题已经成为不同应用者关注的焦点[5-7]。胡耀民，等[8]通过引入信息素更新算子并改进能见度启发因子α，改进了蚁群算法，能准确找出满足路径质量约束的最优路径，但其运行速度较慢；胡启国，等[9]通过重新设计算法的状态转移规则和信息素更新规则，解决了蚁群算法容易陷入局部最优解和搜索时间过长的问题，但其旨在解决最优冗余分配问题。

综上所述，笔者针对高速公路疏散路径问题采用路径分配模型在基础蚁群算法的基础上进行局部更新和全局更新两种信息素更新方式，并采用和分析不同的信息素挥发系数ρ，σ。以河北省高速公路调查数据为基础，建立容量限制动态分配模型，改进路径搜索和交通量分配算法；在基础蚁群算法的基础上引入了μij变量对蚁群的转移规则进行改进，从道路的实际情况出发，进行动态信息素分配，提高算法的收敛速度。通过多组实验数据分析改进模型中的参数最优组合，并以ArcGIS Engine、Visual Studio+C#为开发环境，搭建高速公路应急疏散系统进行疏散路径分析。

1 基于改进蚁群算法路径分析模型

容量限制分配是非平衡模型中的一种动态分配模型，这种分配模型在考虑路段路阻的前提下，可以通过对路径搜寻方法以及交通量加载方法进行改进，并且在交通分配模型中将最优分配与用户随机分配两种方式分配相结合。笔者在孙华灿，等[4]的研究基础上对蚁群算法的转移规则和信息素更新方式进行改进，以提高算法的收敛性和收敛精度。

1.1 交通路阻

在公路上出行者所花费的时间与该路段上的交通流量成正比，其时间与交通量之间的关系可表达为：

ta=f(qa)

(1)

式中：ta为通过路段a所花费的时间；qa为路段a上的交通量。

对于行驶在公路上的时间函数模型有基于交通3参数的路阻函数模型，我国学者将非机动车因素考虑进BPR函数中而提出的路阻函数模型，但是使用最为普遍的还是由美国联邦公路局开发的路阻函数，BPR模型表达式为：

(2)

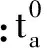
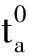
1.2 适用于路径分析的蚁群算法

蚁群算法中的基本变量为[10]：m为蚁群中的蚂蚁数量；n为交通网络中的节点数；τij为边(i,j)上蚁群释放的信息轨迹强度；Δτij(t)为蚂蚁在边(i,j)上留下的单位长度的信息素含量(信息素增量)；α2为信息启发因子，可以表示运动轨迹的重要程度，α2值越大说明蚂蚁趋向于其他蚂蚁所走路径的概率越大；β2为期望启发式因子，反映能见度的重要程度，β2值越大说明转移概率越接近于贪心规则。

1.2.1 转移规则的改进

在基本蚁群算法中，蚂蚁根据随机比例规则进行下一步路径选择，而在改进后的蚁群系统中使用的是伪随机比例规则。第k只在某节点选择下一个允许到达的节点j的规则如式(3)：

(3)

(4)

(5)

(6)

式中：p为蚂蚁k由节点i转移到节点j的转移概率；q为[0,1]上均匀分布的随机数；q0∈[0,1]，为一个参数；allowedk表示蚂蚁k下一步能选择的城市或节点，且allowedk={1,2,3, …,n}-tabuk，tabuk为蚂蚁设置的禁忌表，它记录了当前时刻蚂蚁所搜索过的城市(节点)，约束蚂蚁不能在此次循环中第二次访问这些城市；dij为节点i到节点j之间的距离；tij为从节点i到节点j的行驶时间；qij为节点i到节点j之间的交通容量；μij为路阻的函数，它的引入保证了算法在路径搜索时更倾向于通行时间短和交通容量较大的路段。

在算法的开始阶段，初始化参数时，各路段的初始信息素相差不大，使得ηij和μij可以提供有助于在循环初期算法快速收敛的局部信息。在迭代进行的过程中，信息素会随着路径的搜索而不断改变，这时ηij和μij在体现解信息方面的重要性在不断提高。鉴于此，提出对ηij和μij设计一种倒指数关系曲线以体现其重要性，同时由于在算法迭代过程中行驶时间和交通量对路径影响较大，所以在设计中μij的权重比ηij的权重相对要大一些，故而关系曲线如式(7)、式(8)：

(7)

(8)

式中：NC=1，2，…，NC_max，为当前迭代。

1.2.2 信息素更新方式的改进

由概率选择公式可知，当在一个选择交叉点上时，若其中一个选择的信息素浓度高于其他选择时，蚂蚁选择这个解的概率大，随着循环的不断进行，这条路径上的信息素浓度不断加强，则会导致蚂蚁不断地重复选择同一条路径而出现停滞现象。同时若是某条路径上的信息素浓度过低对进行全局搜索也是不利的。因此根据最大-最小蚁群系统的优化思想，将信息素浓度的取值设定在[τmin, τmax]范围内，要求每一次循环过后，信息素浓度必须符合这个限制：若τij(t)>τmax，取τij(t)=τmax；若τij(t)<τmin，则取τij(t)=τmin。对信息素浓度进行上限设置，避免在路径搜索过程中各路段之间的信息素浓度差异过大；对信息素浓度进行下限设置，避免当某些选择的概率非常小时信息素不至于为0，尽量降低停滞现象发生的机率。τmin和τmax的计算如式(9)、式(10)：

(9)

(10)

式中：Lnn为采用最邻域算法求解初始路径的最短距离。

每一次迭代完成后找出新的最优解Lgb，则τmax按式(11)更新：

(11)

考虑到在迭代不断进行的过程中，信息素浓度的变化，将各路径的初始值设为τmax，可以避免信息素浓度相对之间差异的不断增加，还可以提高算法在初期的寻优能力，改善蚂蚁系统求解最优值的性能。

1)在搜索过程中，若某一条道路上的信息素浓度过高，则会引起路径算法早熟，出现局部最优的情况，因此有必要引入局部更新规则。在局部更新规则中，当蚂蚁k完成某一个路段的搜索后，其所经过路段的信息素按局部更新规则更新。信息素更新规则如下：

(12)

(13)

式中：τ0为初始信息素浓度；N为路网中的节点个数；Lnn为初始最短路径的长度；ρ为信息素局部挥发系数，取值在[0，1]之间，表示信息素挥发的快慢。

2)对信息素进行全局更新是指当所有蚂蚁均完成对所有路径搜索之后，在全局信息素更新中仅允许生成最优解的蚂蚁对信息素进行释放。公式如下：

(14)

(15)

式中：δ∈[0,1]，表示全局信息素衰减系数；R为常数；Lgb为目前迭代中找出的全局最优解。

2 模型的参数分析

由于在算法进行过程中，蚂蚁在选择下一个行驶路段时会根据信息素信息进行判断，因此在每次实验中只改变一个参数，其他参数不变，重复对每一组做20次试验，然后比较所得结果的平均值，目的是消除偶然因素对算法参数的影响。根据高速公路道路网的规模，选取76个节点(最优解108 159)，在ArcGIS中读取这些点状物的坐标，作为算法分析的基础数据，选定起始点和终点不变，根据经验将初始参数设置为α2=1、ρ=0.1，δ=0.1、m=10，NC_max=5 000。笔者提出的改进算法中，大多数变量参数是随着迭代过程中信息素、交通量、路段通行时间的变化而改变。由于没有精确的公式进行初始设置，部分参数根据应用领域的不同而采用不同的取值，因此笔者对α2，ρ，σ，m这4个参数进行实验分析，从而获得参数的最优组合。

2.1 启发因子的实验分析

笔者对α2以0.5为间隔取10个不同的值进行结果比对。α2反映的是在算法进行过程中信息素对蚂蚁进行路径选择的相对重要程度，而当其取值较小时，会减弱信息素对蚂蚁的影响，这时蚂蚁主要受启发信息的影响，容易过早的收敛于局部最优解；当α2的取值较大时，信息素在蚂蚁的移动过程中发挥主要作用，有时会淹没启发信息，所以此时蚂蚁选择已走过路径的概率增大，使得算法结果变差。

图1为算法搜索的迭代次数与全局最优解随α2变化的趋势。由图1可知全局最优解以及算法的迭代次数随着α2不断增大呈近似线性增长的趋势。当α2较小时，算法过早收敛，且容易陷入局部最优解；当α2较大时，收敛速度较慢，由于正反馈作用，使得全局最优解比较大。综合考虑全局最优解及迭代次数，当α2∈[1,2]时，算法的求解性能较好，本研究取α2=1.5。

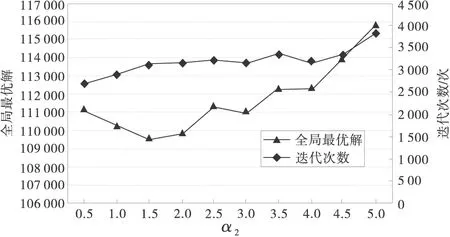
图1 α2对算法运行结果的影响

2.2 局部信息素挥发系数的实验分析

ρ是局部信息素挥发系数，反映某一只蚂蚁完成一次循环后信息素消失的快慢，它是在某一只蚂蚁完成所有节点访问后，对该蚂蚁所走过的路径上的信息素浓度进行调整。当ρ较小时，该蚂蚁所走过的路径上信息素残留较大，容易吸引其他蚂蚁向同一条路径行驶，使算法收敛于局部最优解；当ρ较大时，这条路径上的信息素挥发较快，降低其中某些路段的被选中概率，使得算法收敛速度降低。

图2为ρ的不同取值引起的迭代次数和全局最优解的变化。从图2可知全局最优解在ρ较小或较大时比较敏感，变化趋势较大，因此从最优解的角度取值在区间[0.15，0.5]时，算法比较稳定；若将迭代次数考虑进去，ρ=0.15比较合适。

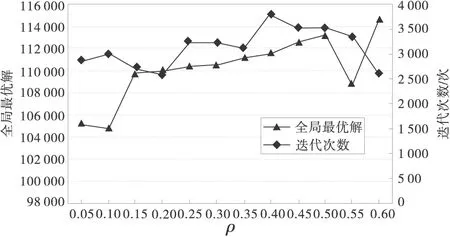
图2 ρ对算法运行结果的影响

2.3 全局信息素挥发系数的实验分析

δ的取值大小对蚁群算法的全局搜索能力和收敛速度有着重要的影响，王颖，等[11]指出δ对蚁群算法的影响是具有双重性的。当δ较小时，将使得未被搜索过的路径上的信息轨迹强度减弱，减小算法的搜索空间，加大陷入局部最优解的可能性，反而增强收敛速度；当δ较大时，搜索过的路径上的信息轨迹强度减弱，扩大了蚁群的搜索范围，从而减低了算法的收敛性，但同时也减小了陷入局部最优解的可能性。

图3是全局挥发系数对算法结果的影响。当δ值较小时，全局最优解较大，且迭代次数也较多；当δ值较大时，全局最优解呈线性增长，这说明δ的增大使得蚂蚁再次选择已搜索过路径的可能性增大，降低了算法的随机性和进行全局搜索路径的能力。从图3中可知当δ在[0.1，0.4)和(0.4,0.5]区间内算法的计算性能稳定，收敛速度和收敛性较好。而且通过对20组值进行最优解及最优解出现次数的分析，可知当δ=0.2时，算法的性能最好。

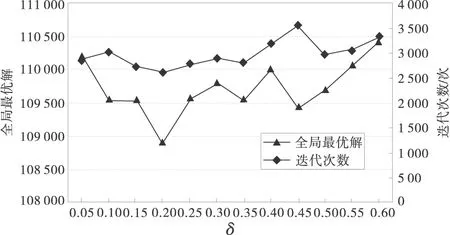
图3 δ取值对算法运行结果的影响

2.4 蚂蚁数量的参数分析

蚁群算法是从多个候选解组成的群体在不断进化的过程中寻找到最优解的，它的优势即为并行搜索[12]。蚂蚁数目较多时，可以增强算法的全局搜索能力和其稳定性，然而当数目过多时，会出现已搜索过的路径上的信息素浓度变化较为接近，降低算法的正反馈作用，使得收敛速度减慢；而当蚂蚁数目过少时，使得已搜索和未被搜索的路径上的信息素浓度差异较大，尤其是当路网规模较大时，将会减弱算法的全局搜索能力和随机性，虽然可以提高算法的收敛速度，但却导致算法稳定性变差。

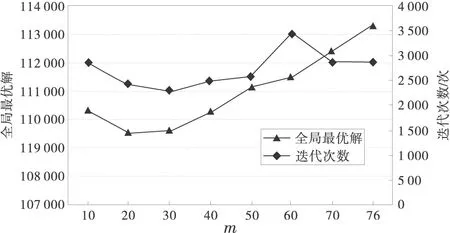
图4 m取值对算法运行结果的影响

表1 蚂蚁数量m与搜索时间的关系

因此通过设定初始值对算法中的参数进行分析，可得到蚁群算法的最优组合为α2∈[1,2]，ρ∈[0.15，0.5]，δ∈[0.1，0.4)∪(0.4,0.5]，m∈ [10，40]。根据实验对最优值与初始值进行对比，最优组合参数为：α2=1.5，ρ=0.15，δ=0.2，m=30；初始设置参数：α2=1，ρ=0.1，δ=0.1，m=10；迭代次数均为5 000。图5是参数更新前后对算法运行结果的影响，参数更新前后的分析结果见表2。

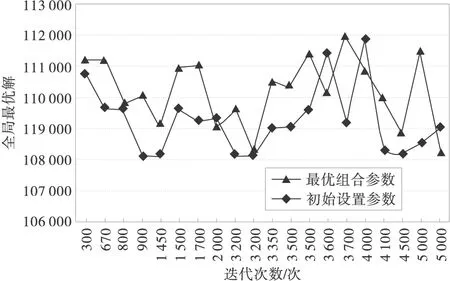
图5 参数更新前后对算法运行结果的影响

表2 参数更新前后的分析结果

对图5和表2分析可知，对蚁群算法的参数采用最优组合后，不但提高了算法的收敛速度，同时也提高了全局搜索能力和算法的稳定性。因此进行路径分析时模型参数的初始值采用最优组合参数。

3 实例分析

3.1 GIS平台及系统设计的基本原理

ArcGIS 10.1是美国环境系统研究公司(Environmental Systems Research Institute, Inc. 简称ESRI)开发的地理信息系统软件，ArcGIS Engine是一个简单的并且可以脱离应用程序ArcObjects编程环境，是建立嵌入式GIS组件的自定义应用程序的类库。Microsoft Visual Studio 2010是面向组件模型COM使用C#语言的一种开发工具，在Visual Studio中新建一个Windows窗体应用程序，可以添加TOCControl、ToolbarControl、MapControl、LicenseControl控件和相关引用。

高速公路应急疏散路径分配以ArcGIS 10.1、ArcGIS Engine以及C#为分析及开发平台。主要技术为：①根据河北省交通图制作ArcGIS的路网矢量图，设置路网属性；②使用ArcCatalog构建网络数据集，为路径分析做准备；③使用C#语言于Visual Studio 2010软件平台编写模型算法程序；④借助ArcGIS Engine进行系统设计，调用ArcGIS 10.1服务引用，实现路径分配。

3.2 高速公路应急疏散路径分析

选取河北省域内交通局域网作为研究对象，其中包含的高速公路与国省干线有G4京港澳高速、G18荣乌高速、G5京昆高速、S52保阜高速(保沧高速)、G107国道、S232省道、S331省道、S335省道、S334省道、S382省道、S241省道、S237省道。通过ArcGIS的网络分析工具条，设置停靠点如图6，假设S52上从P2点向东方向与G107之间出现单向断交情况。根据道路的属性信息，在界面右侧设置需要进行疏散的交通量，疏散点为P1，事故点为P2，目的地为P3，然后进行分析求解。蚁群算法的参数设置见表3，路径分配结果见图6和表4。

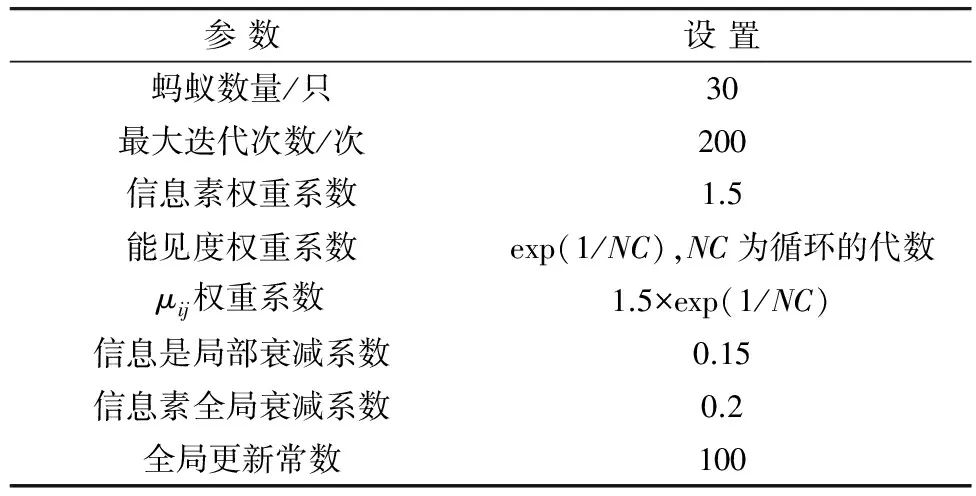
表3 蚁群模型参数设置

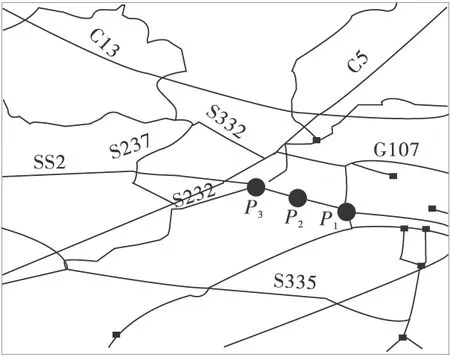
图6 系统分配结果显示

表4 分配结果

3.3 蚁群算法在应急疏散路径中的分析

取路网中节点坐标为基础数据进行计算，比较采用最优参数组合的改进蚁群算法和基础蚁群算法的性能。图7是两种蚁群算法的分析结果。

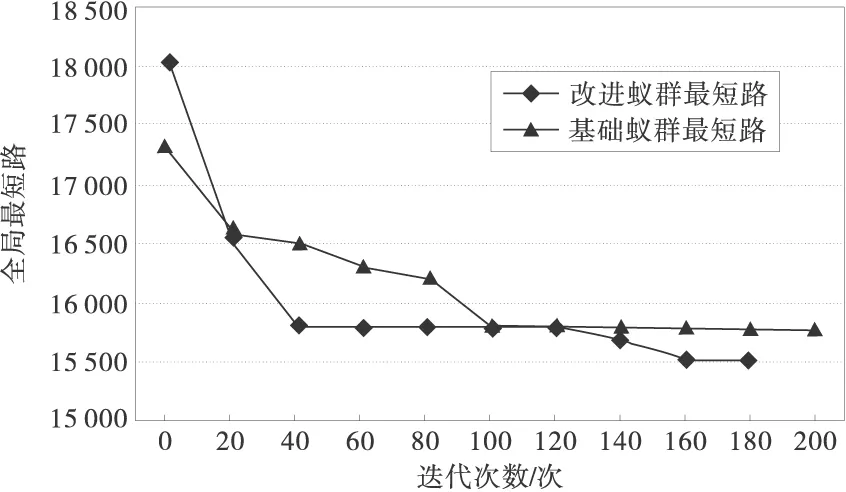
图7 两种蚁群算法的分析结果

对图7进行分析可知，改进蚁群算法在迭代次数为40次与120次之间保持稳定，不再更新最优解，但在140次迭代之后再次开始全局更新直至接近160次时搜索到全局最优解，待全局最优解不再更新之后停止迭代，算法结束；而基础蚁群算法在100次与140次循环之间保持稳定，从第160次迭代开始最短路径长度发生微小变化之后，在第200次迭代时停止，算法结束。由此可知改进的蚁群算法节省了20次迭代所用的时间，加快了算法的运行和收敛速度。

改进蚁群算法虽在蚁群开始移动初期搜索的最短距离大于基础蚁群，但在算法进行过程中逐渐显示优势，蚁群搜索的最短路径长度出现较明显的差异。改进蚁群算法的全局最优解的路径比基础蚁群全局最优解的路径长度缩短近300 m，优化了全局最优解并且提高了收敛精度。

4 结 论

在分析高速公路路段阻抗的基础上，从路径分配模型参数研究入手，采用改进的蚁群算法求解交通事件发生时高速公路应急疏散路径问题，得到如下结论：

1)采用改进的蚁群算法可以提高算法的搜索速度和收敛性，本研究引入μij函数作为蚂蚁的转移规则，可以更好的体现容量限制分配中路阻的影响作用，使蚂蚁在进行下一个路段选择时更倾向于通行时间短，交通容量大的路段，更加切合驾驶员行驶过程中的路径选择行为。

3)以ArcGISEngine和C#作为分析及开发平台，设计高速公路应急疏散系统，对应急疏散路径进行分析，实现系统可视化疏散路径，便于出行者对疏散路径的理解和选择，同时方便管理者决策。

[1] 王旭,崔平远,陈阳舟．基于蚁群算法求路径规划问题的新方法及仿真[J]．计算机仿真,2005,22(7):60-62.WangXu,CuiPingyuan,ChenYangzhou.Anewmethodandsimulationforpathplanningproblembasedonantcolonyalgorithm[J].ComputerSimulation,2005,22(7):60-62.

[2] 刘勇．基于蚁群算法的应急救援最优路径研究[D]．武汉:中国地质大学,2010. Liu Yong.The Research on the Optimal Path of Emergency Rescue Based on Ant Colony Algorithm[D].Wuhan:China University of Geosciences,2010.

[3] 徐勋倩,黄卫．蚂蚁算法处理动态交通网络用户均衡配流问题[J]．公路交通科技,2005,1(1):111-114. Xu Xunqian,Huang Wei.Ant algorithm for users equilibrium assignment model of dynamic traffic network[J].Journal of Highway and Transportation Research and Development,2005,1(1):111-114.

[4] 孙华灿,李旭宏,刘艳忠,等．容量限制分配的蚁群优化算法[J]．东南大学学报:自然科学版,2009,39(1):177-180. Sun Huacan,Li Xuhong,Liu Yanzhong,et al.Ant colony optimization arithmetic of capacity restraint traffic assignment[J].Journal of Southeast University:Natural Science,2009,39 (1):177-180.

[5] 詹士昌,徐婕,吴俊.蚁群算法中有关算法参数的最优选择[J].科技通报,2003,19(5):381- 386. Zhang Shichang,Xu Jie,Wu Jun.The optimal selection on the parameters of the ant colony algorithm[J].Bulletin of Science and Technology,2003,19(5):381- 386.

[6] 徐红梅,陈义保,刘加光,等.蚁群算法中参数设置的研究[J].山东理工大学学报:自然科学版,2008,22(1):7-11. Xu Hongmei,Chen Yibao,Liu Jiaguang,et al.The research on the parameters of the ant colony algorithm[J].Journal of Shandong University of Technology:Natural Science,2008,22(1):7-11.

[7] 叶志伟,郑肇葆.蚁群算法中参数α,β,ρ设置的研究——以 TSP 问题为例[J].武汉大学学报:信息科学版,2004,29(7):597-601. Ye Zhiwei,Zheng Zhaobao.Configuration of parametersα,β,ρin ant algorithm[J].Geomatics and Information Science of Wuhan University,2004,29(7):597-601.

[8] 胡耀民,刘伟铭.基于改进型蚁群算法的最优路径问题求解[J].华南理工大学学报:自然科学版,2010,38(10):105-110. Hu Yaomin,Liu Weiming.Solving of optimal path problem based on improved ant colony algorithm[J].Journal of South China University of Technology:Natural Science,2010,38(10):105-110.

[9] 胡启国,胡小华,吴泳龙．改进蚁群算法在系统可靠度最优冗余分配的应用[J].重庆交通大学学报:自然科学版,2013,32(3):543-546. Hu Qiguo,Hu Xiaohua,Wu Yonglong.Application of improved ant colony algorithm in system reliability optimization of redundancy allocation[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(3):543-546.

[10] Bonabeau E,Dorigo M,Theraulaz G.Swarm Intelligence:From Natural to Artificial Systems[M].New York:Oxford University Press,1999,10-32.

[11] 王颖,谢剑英.一种自适应蚁群算法及其仿真研究[ J].系统仿真学报,2002,14(1):31-33. Wang Ying,Xie Jianying.An adaptive ant colony optimization algorithm and simulation[J].Journal of System Simulation,2002,14 (1):31-33.

[12] 覃刚力,杨家本.自适应调整信息素的蚁群算法[J].信息与控制,2002,31(3):198-201. Tan Gangli,Yang Jiaben.An improved ant colony algorithm based on adaptively adjusting pheromone [J].Information and Control,2002,31(3):198-201.

Study on Highway Evacuation Route Based on Improved Ant Colony Algorithm

Li Qiaoru1,2, Zhang Qian1, Chen Liang1,2, Cui Ning1

(1. College of Civil Engineering, Hebei University of Technology, Tianjin 300401, China; 2. Civil Engineering Technology Research Center of Hebei Province, Tianjin 300401, China)

According to the characteristics of expressway emergency evacuation, improved ant colony algorithm was applied in traffic assignment models. Firstly, the function of traffic flow and capacity was introduced as a part of the algorithm state transition rules. Consequently the paths with larger capacity and shorter travel time were chosen preferentially when searching. Secondly, the influences of ant colony algorithm parameters on calculation results and the convergence speed were studied by experimental analysis, then the optimal combination of algorithm parameters were presented accordingly. Finally, the optimal parameter combination was applied to the improved ant colony algorithm, and the searching results were compared with the basic ant colony algorithm through simulation experiments. The results show that ant colony algorithm with the optimal combination parameter has advantages in accelerating the search speed and optimizing the global optimal solution. The visual emergency evacuation paths are available through the path analysis via expressway emergency evacuation system based on GIS.

traffic engineering; evacuation route; ant colony algorithm; parametric analysis

10.3969/j.issn.1674-0696.2015.03.19

2013-11-21；

2014-03-06

河北省人力资源与社会保障厅留学人员科技活动项目(D2011001)；河北省高等学校科学技术研究重点项目(ZD2014078)

李巧茹(1972—)，女，河北石家庄人，副教授，博士，主要从事交通运输规划管理与控制方面的研究。E-mail：qiaoruli129@126.com。

U495

A

1674-0696(2015)03-086-07