新疆融雪型灾害对沿河路基局部冲刷深度计算

吴国雄，王 韬，周 宇，余 苗

(重庆交通大学 土木建筑学院，重庆 400074)



新疆融雪型灾害对沿河路基局部冲刷深度计算

吴国雄，王 韬，周 宇，余 苗

(重庆交通大学 土木建筑学院，重庆 400074)

以新疆山区小流域为研究对象，在正确估算最大融雪径流量的基础上，对沿河路基结构物在纵横水流交汇处附近的水流特征、冲刷机理及冲刷深度和范围的影响因素进行了分析；通过室内模型试验，得到了单个影响因素与路基边坡坡底冲刷深度的关系图，对纵、横两个方向的不同流量、流速和河流水深、山坡坡度、路基边坡、路基宽度和泥沙粒径等条件下沿河路基的冲刷进行了试验模拟，并根据试验结果，建立了沿河路基在纵横水流交汇处最大冲刷深度的计算公式，验证其有效性。

道路工程；融雪型洪灾；沿河路基；纵横水流；冲刷机理；局部冲刷深度

洪水灾害是当今世界上发生最频繁和危害最大的自然灾害之一[1-5]。我国南方多雨山区，暴雨造成的坡面水流和河道水流对铁路和公路的冲刷破坏最严重[6]，而在我国新疆等积雪广布、春洪和雪灾多发的地区，每到春融季节融雪型洪灾频频发生[7]，积雪融化补给河流[8]，常发生春季融雪形成的大量洪水冲刷路基而造成沿河线路路基大范围的坍塌破坏，对河床和路基的冲刷也较为强烈，轻者会造成线路及其设施的破坏，影响交通安全，重者直接会断道而中断交通，对人民生命财产的安全等造成重大的损失。

暴雨或融雪型洪水对沿河线路路基造成的水毁具有其自身特殊性：既有横向来至山坡汇流而形成的洪水，又有纵向来至河流的洪水，山坡洪水和河流洪水的共同作用对路面的冲刷及路基边坡的淘刷而破坏路基的整体稳定性。笔者针对新疆小流域内，在正确估算小流域的最大融雪径流量的基础上[9]，分析沿河路基冲刷影响因素[10-11]，对路基在纵横水流交汇处附近的水流特征、冲刷机理进行了分析。通过室内模型试验[12-13]，得到了单个影响因素与路基边坡坡底冲刷深度的关系图，对纵横两个方向的不同流量、流速和河流水深、山坡坡度、路基边坡、路基宽度和泥沙粒径等条件下沿河路基的冲刷进行了试验模拟，根据试验结果并结合理论分析，建立了纵横水流交汇处沿河路基最大冲刷深度的计算公式并进行了验证。

1 沿河路基水流交汇处局部冲刷模型试验

本次试验是室内模型试验，试验地点为重庆交通大学内河航道国家工程中心。模型为自行设计，主要由主河槽、有机玻璃水槽和路基组成，如图1。

图1 试验模型布置

试验采用循环供水系统模式，实验室水泵最大可提供100 L/s的流量。整个试验循环系统有2 m×2 m的稳流蓄水池、量水堰、尾部调节阀门、循环水道、水位测针等系列装置。模型水槽的槽头设有前池和稳流栅，槽尾设有尾水池(沉沙池)，以保证水流的稳定。流量由水槽槽首的三角薄壁堰和槽尾调节阀门来调控，试验水位采用水位测针进行监控与测量，水流流速采用LS-6级流速仪测量，水深、路基冲刷深度和路基边坡坡底局部冲刷深度采用光纤式Ⅱ型测深仪进行量测。

1)流量。河流纵向水流量由底宽为60 cm的直角三角形薄壁堰来控制，如图2。

图2 直角三角形薄壁堰

山坡横向水流量由底宽为30 cm的直角三角形薄壁堰来控制，其流量计算式如式(1)：

Q=C0H5/2

(1)

(2)

式中：C0为直角三角形薄壁堰的流量系数；Q为流量，m3/s；H为堰顶水头，m；P1为上游堰高，m；B为堰上游引渠宽，m。

2)水深。为了研究不同水深情况下纵横水流交汇处的冲刷特点，河流纵向水流量的堰顶水深分别采用0.123 3，0.142 0，0.166 0m。山坡横向水流量的堰顶水深分别采用0.065，0.081，0.096m。

3)坡底。由于山区河流河床比降较大，并结合场地，水槽坡底纵比降采取2%。

4)泥沙。试验采用无黏性砂作为试验砂，中值粒径d50=0.5，1.5，7.75，29.5mm。

此试验主要是在不同的横向山坡流量、纵向河流水深、泥沙、流速和几何边界条件下，观测路基冲毁程度、护墙墙底的冲刷范围及深度、冲刷发展的过程及护墙附近的水流形态。在水流冲刷的作用下，山坡水流直接冲毁路面、交汇处形成螺旋水流对护墙墙底被淘刷的效果很明显。

从冲刷的时程来看，冲刷深度在前1h左右变化较大，之后增加速率逐渐变小，试验冲刷5～6h后，冲刷深度基本稳定，之后冲刷发展就十分缓慢，且变化程度很小。可见，采用5～6h的冲刷历时是比较合理的。

2 沿河路基水流交汇处局部冲刷特征及冲刷深度影响因素分析

2.1 水流交汇处局部冲刷特征

横向融雪水流沿山坡冲向路基，在惯性力的作用下沿着路基边坡流向河道，受到纵向河道水流的制约，两个方向水流在路基坡脚处汇合，使得交汇处水流形态发生变化。如图3，山坡水流经过边坡、路面缓冲和路基后，若以山坡沟心为中心线，会形成中间水流流量和流速较大、两端较小的态势。河流中的纵向行进靠近交汇处，由于横向山坡水流O1到O段的流速和流量逐渐增大，两向水流结合后会形成A1到A2段成型螺旋水流，横向水流的一部分将纵向水流表层推开至远离坡脚，减小横向水流向坡脚的下蚀阻力，两方向大部分水流形成逐渐增大并向下侵蚀淘坡脚的螺旋流。同时，由于O1到O段纵向流表层已被推开，而A2到B1段的表层螺旋水流还来不及回到坡面，且O到O2段的水流流量和流速最大，导致A2到B1段比A1到A2段的表层水离墙面更远，纵向流对横向流下蚀坡脚的阻力就更小，故形成的螺旋水流对墙底的冲刷能力比O1到O段大。从A2到B1段下层水流的冲刷力将出现逐渐减小的趋势，整个坡底被冲刷淘蚀的最大地点将会出现在A2偏后位置。随着上游两方向形成的螺旋水流对坡脚的淘刷，使得部分泥沙下移，逐渐堆积在B1到B2段，加上O2到O3的横向流量和流速逐渐减小，且有泥沙的阻挡作用，因而该段交汇水流对坡脚淘刷能力较小。

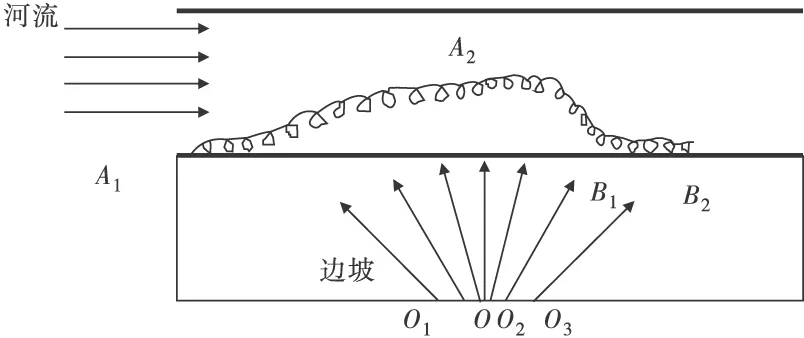
图3 交汇处的水流形态

2.2 水流交汇处冲刷深度的影响因素

水流交汇处路基的局部冲刷由路基边坡和防护工程、水流、河床泥沙共同作用，使附近河床产生局部变形，因此，影响局部冲刷深度的因素可以归纳为水流、河床质和几何边界条件等3个方面。

2.2.1 水流因素

1)河流上游行进水深h

试验表明，在其它条件不变的情况下，河流中上游的行进水深较小时，交汇处局部最大冲刷深度随水深的增加而增加。但当水深增大到一定程度时，由于河流对山坡水流的阻挡作用，局部最大冲刷深度不再随上游水深的增加而增大，如图4。

图4 行进水深与路基边坡坡底冲刷深度关系

2)流速V

当水流行进流速达到床面泥沙起冲流速时，开始产生局部冲刷，以后冲刷坑深度随流速的增大而增加。但当行进流速大于床面泥沙的起动流速以后，由于床面泥沙对冲刷坑产生某种补偿作用，使得局部冲刷深度随流速的增大而增加的趋势明显减缓。国内外对桥墩和丁坝局部冲刷研究已证明，当V达到起动流速后，泥沙开始以沙坡形式向前推移。因此，进入冲刷坑的泥沙时多时少，导致冲刷坑也相应地时深时浅(hs值是波动的)，当V增大到一定数值，沙坡消失，泥沙以层状向前移动，此时，hs的增大才停止，随后有所减少。

3)流量Q

此处流量是指交汇处山坡横向最大融雪径流量，主要与融雪面积和积雪厚度、降雨量大小和地形特征等因素有关。在其他条件不变情况下，流量越大，通过路面后形成的单宽流量和势能愈大，冲刷的范围和坡脚的冲刷深度愈大，如图5。

图5 山坡流量与路基边坡坡底的冲刷深度关系

2.2.2 河床质因素

河床泥沙可分为非黏性泥沙和黏性泥沙。非黏性泥沙对冲刷深度的影响因素主要是泥沙的粒径，包括级配、平均粒径等，而黏性泥沙还与黏性土的含量、特性、类型、黏土的固结和压缩状态有关[14]。

目前普遍认为，泥沙特征对冲刷的过程影响很大。如果泥沙很粗，实际水流未达到使其起动条件，就不会发生冲刷；或者河床由粒径不同的砾石和泥沙组成，细的颗粒可能被水流冲走，粗的颗粒不能起动而被留下来，逐渐形成一个覆盖层，当其覆盖层达到一定厚度时，足以保护下层泥沙不会被冲走，此时停止冲刷；或河床泥沙比较细，能全部起动，则冲刷现象会迅速发生，但冲刷达到一定程度之后，流速降低，水深增加，水流条件不会使泥沙继续起动时，则停止冲刷。

泥沙的粒径对局部最大冲刷深度和起动流速有着明显影响，当中值粒径增大时，起动流速也会增大，对应的冲刷深度反而减小，如图6。

图6 河沙中值粒径d50与路基边坡坡底冲刷深度关系

2.2.3 几何边界因素

几何边界特征因素主要有山坡坡度m1、山坡主水流与道路路基的交角θ、路基宽度W和路基边坡坡度m2。试验表明：山坡坡度愈陡，汇成水流的动能转化成势能就越大，冲刷强度就越大；路基越宽，对水流的缓流作用就越强，对坡脚的冲刷相对愈小；路基边坡愈缓，对于减小局部最大冲刷深度作用就越明显。除了这些以外，防护措施的结构形式、几何尺寸等对冲刷深度也有影响，如设置阶梯，逐步减小横向山坡水流的冲刷能量等，如图7、图8。

图7 边坡坡度与路基边坡坡底冲刷深度关系

图8 路基宽度与路基边坡坡底冲刷深度关系

3 沿河路基水流交汇处局部冲刷深度计算公式

根据完成的不同几何边界、水流和泥沙条件下的路基边坡坡脚交汇水流处局部冲刷试验的资料来看，影响纵横水流交汇处冲刷深度的因素较多。初步可用式(3)来表示：

hs=f(Q,m1,m2,W,h,d50,V,θ)

(3)

式中：hs为交汇处局部最大冲刷深度，从平均河床面高程计，m；m1为山坡坡度系数；m2为路基边坡坡度系数；W为路基宽度系数；h为交汇处上游水深，m；d50为河沙中值粒径，mm；Q为山坡横向最大融雪径流量，L/s；V为交汇处上游行进流速，m/s；θ为主水流与道路路基的交角，(°)。

通过对局部冲刷影响因素的多元逐步回归分析和量纲分析，剔除影响不显著的影响因素，寻求沿河路基横纵水流交汇处局部最大冲刷深度hs与主要影响因素的关系，如式(4)：

(4)

式中：km1为山坡坡度系数；km2为路基边坡坡度系数；kW为路面宽度系数；Fr为行进水深佛汝德数，Fr=V2/gh；a，b，c，k分别为待定指数、系数；其他参数同前。

根据试验结果，图9分别为对山坡坡度系数、路基边坡坡度系数、路基宽度系数分析的结果，得到各自与纵横交汇处路基局部冲刷深度关系曲线，关系如式(5)～式(7)：

km1=0.083 1e-1.003 9m1

(5)

km2=0.295 8e-1.339 9m2

(6)

kW=0.062 9e-0.398m2

(7)

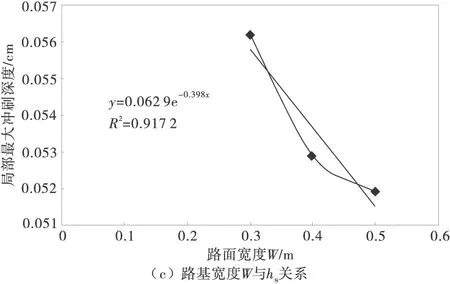
图9 山坡坡度系数、路基边坡坡度系数、路基宽度系数与局部最大冲刷深度的关系

对式(4)两边取对数，则有式(8)：

(8)

根据本次试验搜集到的局部资料进行多元线性回归，可得到各参数结果：k=357.889，a=0.207，b=0.218，c=0.674 1。

将上述参数代入式(4)得：

hs=357.889(0.083 1e-1.003 9m1)(0.295 8e-1.339 9m2)·

(9)

简化得：

(10)

式(10)考虑了流速、水深、路基宽度、粒径因素、山坡坡度系数、路基边坡坡度系数、山坡融雪流量，但式(10)只适用于山坡洪水与河流交汇冲刷处路基尚未冲断情况下的坡脚局部冲刷深度的计算。

图10是实测冲刷深度与利用式(10)预测冲刷深度的对比，其相关系数R= 0.907 3，可见两者吻合较好。

图10 hs实测值与hs预测值的对比

4 结 论

1)试验分析表明，山坡洪水与河流交汇处的沿河路基坡脚冲刷深度的影响因素较为复杂，主要有河道水流条件、河床质特征、山坡洪水流量和道路几何边界等，其中，山坡洪水流量和道路几何边界影响较为显著，由此而形成的路基交汇处局部冲刷特征与一般河道路基的冲刷特征差异较大。

2)室内水槽模型试验表明，山坡水流直接冲毁路面、交汇处形成螺旋水流，对护墙墙底淘刷效果较为明显。从冲刷时程看，冲刷深度在前1 h左右变化较大，而在其以后增加速率逐渐变小，冲刷5～6 h后冲刷深度基本稳定，之后冲刷发展十分缓慢，可见，采用5～6 h的冲刷历时是比较合理的。

3)通过对多因素条件下沿河路基交汇处坡脚局部冲刷进行分析，运用量纲理论和回归分析方法得出了沿河路基坡脚的局部最大冲刷深度计算公式，利用该公式计算的交汇处局部冲刷深度与实测值吻合较好。同时，该公式考虑了流速、行进水深、路基宽度、粒径因素、山坡坡度、路堤边坡、山坡洪水流量等因素，能估算山洪和河水综合作用下路基局部冲刷深度并指导路基防护设计。

[1] 水利电力部水文局.中国水资源评价[M].北京:水利电力出版社,1987. Ministry of Water Resources Hydrology Bureau.Evaluation of Water Resources in China[M].Beijing:China Water & Power Press,1987.

[2] 骆承政,乐嘉祥.中国大洪水——灾害性洪水述要[M].北京:中国书店,1996. Luo Chengzheng,Le Jiaxiang.Flood in China-Introduction of Devastating Flood[M].Beijing:China Bookstore,1996.

[3] 张行南,罗健,陈雷,等.中国洪水灾害危险程度区划[J].水利学报,2000(3):1-7. Zhang Xingnan,Luo Jian,Chen Lei,et al.Zoning of Chinese flood hazard risk[J].Journal of Hydraulic Engineering,2000(3):1-7.

[4] 张欧阳,许炯心,张红武,等.洪水的灾害与资源效应及其转化模式[J].自然灾害学报,2003,12(1):25-30. Zhang Ou’yang,Xu Jiongxin,Zhang Hongwu,et al.Flood hazards and resources effects and their inter-transform mode[J].Journal of Natural Disasters,2003,12(1):25-30.

[5] 高吉喜,潘英姿,柳海鹰,等.区域洪水灾害易损性评价[J].环境科学研究,2004,17(6):30-34. Gao Jixi,Pan Yingzi,Liu Haiying,et al.Assessment on regional vulnerability to flood[J].Research of Environmental Sciences,2004,17(6):30-34.

[6] 黄志才,吴国雄,程尊兰.川藏公路沿河路基水毁成因分析与工程防护[J].水土保持通报,2003,23(4):21-23. Huang Zhicai,Wu Guoxiong,Cheng Zunlan.Research on causes and prevention methods of water damage to Sichuan-Tibet highway[J].Bulletin of Soil and Water Conservation,2003,23(4):21-23.

[7] 刘志辉.基于“3S”技术的新疆融雪洪水预测预警及决策支持研究[D].徐州:中国矿业大学,2009. Liu Zhihui.The Prediction,Early-Warning for Snowmelt Flood and Decision Support based on ‘3S’ Technologies in Xinjiang[D].Xuzhou:China University of Mining and Technology,2009.

[8] 张一驰,李宝林,包安明,等.开都河流域融雪径流模拟研究[J].中国科学D辑:地球科学,2006,36 (增刊2):24-32. Zhang Yichi,Li Baolin,Bao An’ming,et al.Research on the simulation of Kaidu River`s snowmelt runoff[J].Science in China Series D:Earth Sciences,2006,36 (Sup2):24-32.

[9] 于海鸣,刘建基.新疆丘陵区小流域春季融雪设计洪水估算[J].水利规划与设计,2005(3):25-28. Yu Haiming,Liu Jianji.Estimating design flood of the spring snow melt in Xinjiang[J].Water Resources Planning and Design,2005(3):25-28.

[10] 田伟平,李惠萍,高冬光.沿河路基冲刷机理与冲刷深度[J].长安大学学报:自然科学版,2002,22(4):39-42. Tian Weiping,Li Huiping,Gao Dongguang.Scour depth and mechanism of highway subgrade along river[J].Journal of Chang’an University:Natural Science Edition,2002,22(4):39-42.

[11] 吴国雄,黄志才.沿河路基局部冲刷深度计算研究[J].中国公路学报,2005,18(4):12-15. Wu Guoxiong,Huang Zhicai.Research on local scour depth calculation of roadbed along river[J].China Journal of Highway and Transport,2005,18(4):12-15.

[12] 杜明格,刘国东.无资料地区径流量计算方法的探讨[J].重庆交通大学学报:自然科学版,2007,26(4):138-141. Du Mingge,Liu Guodong.Discussion on the runoff calculation method for the area no data recorded[J].Journal of Chongqing Jiaotong University:Natural Science,2007,26(4):138-141.

[13] 童思陈,高建,许光祥,等.弯道水流纵向垂线平均流速分布的计算[J].重庆交通大学学报:自然科学版,2009,28(1):126-129. Tong Sichen,Gao Jian,Xu Guangxiang,et al.Calculation of the longitudinal depth averaged velocity distribution of curved conduit flow[J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(1):126-129.

[14] Ansari S A.Influence of cohesion on scour and bridge piers[J].Journal of Hydraulic Research,2002,40 (6):717-729.

Local Scour Depth Calculation of Roadbed along River Causing by Snowmelt Disasters in Xinjiang

Wu Guoxiong, Wang Tao, Zhou Yu,Yu Miao

(School of Civil Engineering & Architecture, Chongqing Jiaotong University, Chongqing 400074, China)

Xinjiang mountain watershed was taken as the object of the research. On the foundation of exactly estimating the max snowflow discharge, the influence factors of structures along the river embankment in the aspect of water flow characteristics, scour mechanism and scour depth and scope near the junction were analyzed. Indoor lab experiments were carried out to simulate the scour. Firstly, the relationship between each influence factor and the slop erosion depth was found out. Then the slop erosion under different flow quantity, flow rate, water depth, hill slop gradients, side slope gradient, subgrade depth and sand particle size were simulated. Finally the maximum erosion depth was gained by the above lab results and theoretical analysis, and its validity was checked.

road engineering; snowmelt floods; river side subgrade; water from longitudinal and lateral direction; scour mechanism; local scour depth

10.3969/j.issn.1674-0696.2015.03.12

2014-04-09；

2014-04-11

重庆交通大学交通土建工程材料国家地方联合工程实验室开放基金项目(LHSYS-2012-006)；重庆市高校优秀成果转化项目(KJZH14104)

吴国雄(1966—)，男，湖北崇阳人，教授，博士，主要从事道路工程方面的研究。E-mail: wgx_ph.d@163.com。

U416.1

A

1674-0696(2015)03-057-06