发动机变阻尼扭振减振器的轴系扭振抑制分析

舒歌群，王 斌，梁兴雨

发动机变阻尼扭振减振器的轴系扭振抑制分析

舒歌群，王 斌，梁兴雨

(天津大学机械工程学院，天津 300072)

以发动机曲轴系扭转振动为研究对象，分析了扭振减振器阻尼比参数的变化对轴系扭转振幅放大系数的影响，并开展了轴系变阻尼扭振减振器的设计工作．计算结果表明：装配变阻尼扭振减振器后，系统的自振频率和临界转速都相应有所升高；当变阻尼扭振减振器在各临界转速下选取最佳阻尼值时，轴系自由端各阶扭转振幅均有明显降低，显著改善了发动机的扭转振动特性，验证了变阻尼扭振减振器对轴系扭转振动抑制的有效性．

变阻尼；扭振减振器；轴系扭振；强迫振动

一直以来，对发动机曲轴系振动的研究主要围绕扭转振动进行，常见的减振方法[1]是在曲轴自由端安装阻尼扭振减振器，如硅油减振器、橡胶减振器等．近年来，随着发动机向高速化、高效化、低污染等方向发展，再加上增压中冷技术、废气再循环、高压缩比、长行程等新技术的应用，增加了发动机曲轴系所承担的机械负荷．这些新技术对发动机的可靠性提出了新的要求[2]．越来越多的学者对原有阻尼扭振减振器进行了深入研究[3-4]，研究方向从定值阻尼减振器发展到变阻尼扭振减振器[5-6]；也有学者利用曲轴飞轮端或联轴器进行扭振抑制研究[7-8]，但并没有得到普遍应用．

尽管很多人已经通过理论和实验研究提高了定值阻尼扭振减振器的减振效果，但关于发动机曲轴系变阻尼扭振减振器的研究却鲜见报道．本文以曲轴自由端安装变阻尼扭振减振器的轴系扭振模型为研究对象，探讨了变阻尼扭振减振器对发动机轴系扭振特性的影响．

1 建立集总参数模型

对发动机曲轴系扭转振动的分析，常将整个轴系当量简化成无阻尼单自由度系统[1]．在曲轴自由端安装扭振减振器后，以轴系1阶扭转共振频率为研究对象，整个轴系可以简化成2自由度强制振动系统，如图1所示.

图1 轴系等效模型Fig.1 Equivalent model of crankshaft system

根据D’Alombert原理[9]，图1所示系统的运动微分方程为

式中：gϕ、dϕ分别为发动机当量轴系和扭振减振器的扭角角度；gI、dI分别为发动机当量轴系和扭振减振器的转动惯量；gK、dK分别为发动机当量轴系和扭振减振器的扭转刚度；dδ为阻尼系数；M′为干扰力矩；w为干扰力频率．式(1)可用矩阵表示为

设式(2)之解为

将式(3)代入式(2)整理后，得

求解矩阵方程(4)，可得

所以有

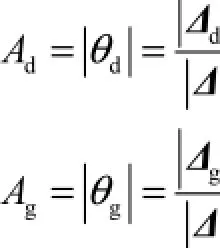
式中：dA为扭振减振器惯性体的振幅；gA为发动机当量静振幅．由此可求出发动机曲轴的扭转振幅放大系数为

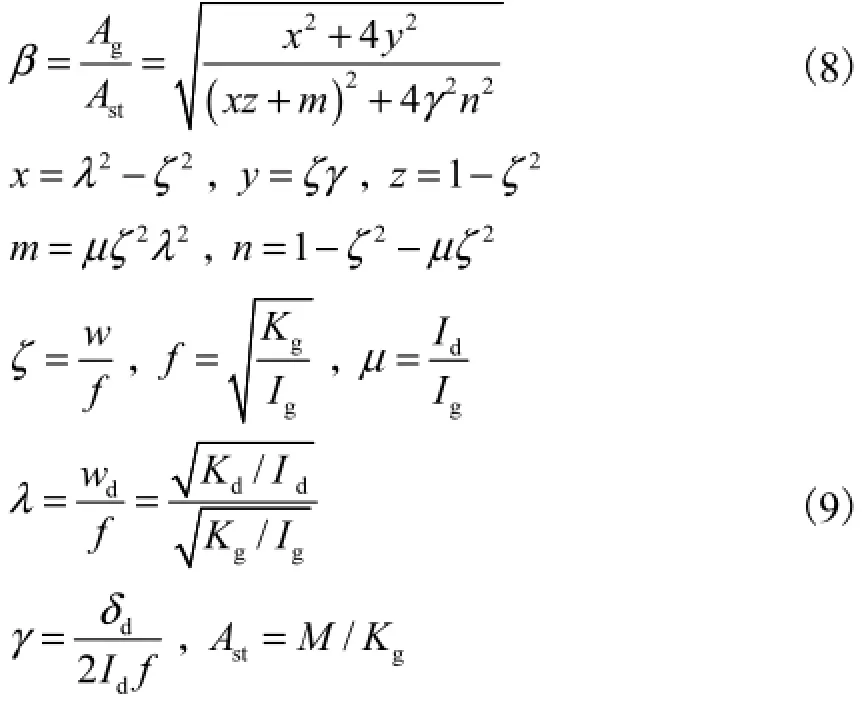
式中：stA为轴系当量静振幅；f为曲轴轴系自振频率；ζ为频率比；λ为扭振减振器定调比；μ为惯量比；γ为阻尼比.

2 参数分析

由式(8)可知，轴系扭转振幅放大系数是扭振减振器定调比、阻尼比、惯量比与轴系强制振动的频率比的综合函数，其扭转振幅放大系数随频率比的变化与定调比、惯量比和阻尼比系数有关．为了使减振器有良好的减振效果，必须恰当地选择这3个参数．其中，定调比是减振器的重要参数，可按式(9)设计．欲使轴系扭振振幅在发动机工作转速范围内的变化较为平坦，避免出现较大峰值，一般使定调比在0.75～1.00之间[10]，有时为了降噪甚至可以选择大于1.00的定调比．

对于变阻尼扭振减振器来讲，可通过改变阻尼值使减振器在轴系各个临界转速(共振转速)下都有较好的减振效果，所以在分析变阻尼扭振减振器对轴系扭振的影响时，其惯量比、定调比可视为一常数，只需分析不同频率比的情况下阻尼比对扭转振幅放大系数的影响，所以，本文研究了当减振器惯量比、定调比不变时，在不同轴系频率比的情况下，改变扭振减振器的阻尼比，其扭转振幅放大系数曲线的变化规律，如图2所示．

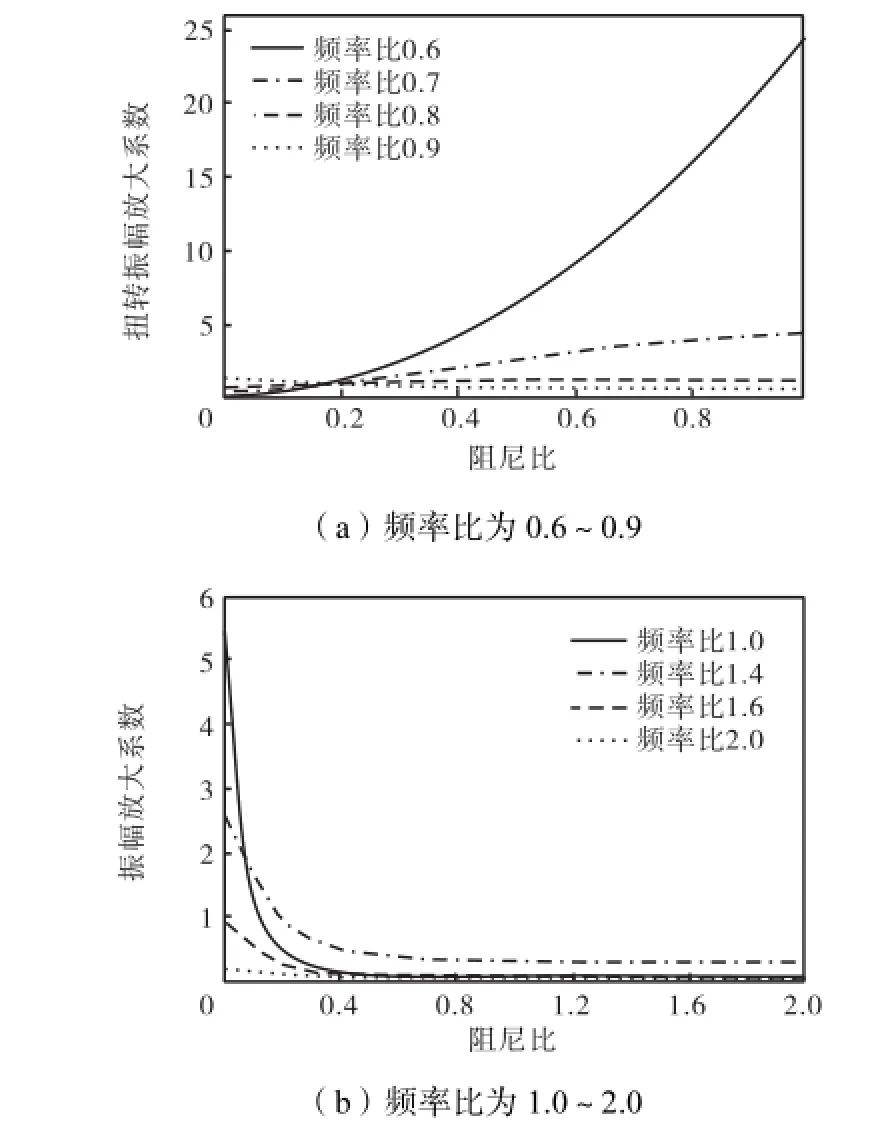
图2 阻尼比对扭振减振器振幅放大系数的影响Fig.2 Influence of different values of γon torsional amplitude amplification coefficient

当变阻尼扭振减振器惯量比、定调比取某一常数时，由图2(a)可知，对于不同轴系频率比来讲，扭转振幅放大系数曲线一般呈现单增或单减的趋势．当频率比小于0.7时，扭转振幅放大系数随减振器阻尼比的增大而增大，频率比越小，其增幅越大；而当轴系频率比大于0.7时，扭转振幅放大系数随阻尼比的增大而减小．由图2(b)可知，当频率比等于1.0时，其扭转振幅放大系数曲线减幅最大，并且在较小阻尼比值处的扭转振幅放大系数明显大于其他频率比下的扭转振幅放大系数，这说明在频率比等于1.0的情况下，阻尼比在0～0.2取值范围内的变化对扭转振幅放大系数有较大的影响．所以，在设计变阻尼扭振减振器时，需分析扭振减振器阻尼比参数的变化对轴系扭转振幅放大系数的影响，并在不同频率比的情况下选取适当阻尼比值来达到理想的减振效果．

3 算例及结果分析

3.1 曲轴系扭转振动分析

本文以某发动机曲轴系为例，采用第1节中集总参数模型，使用系统矩阵法进行计算，将发动机曲轴系离散为7个集中质量模型，如图3所示．其中：I1为皮带轮、正时齿轮以及曲轴自由端连接头转动惯量之和，kg⋅m2；I2～I5分别为单位气缸当量扭转惯量，kg⋅m2；I为飞轮连接端和飞轮的转动惯量之和，6kg⋅m2；K～K分别为各质量间连接轴段的扭转刚15度，N⋅m/rad；δn,n+1为第n、n＋1集中质量之间的阻尼系数，N⋅m⋅s/rad，n＝1，…，5．

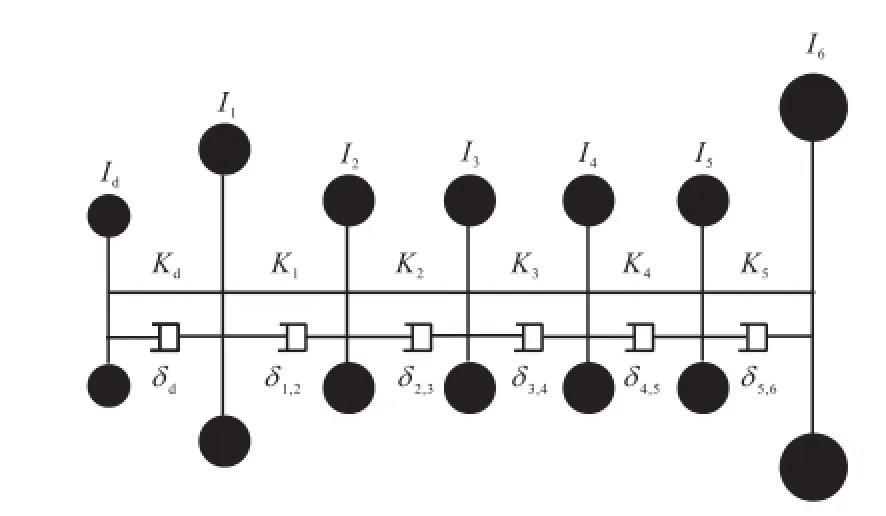
图3 发动机轴系当量系统Fig.3 Engine shafting equivalent system

该离散化模型各参数值如表1所示．

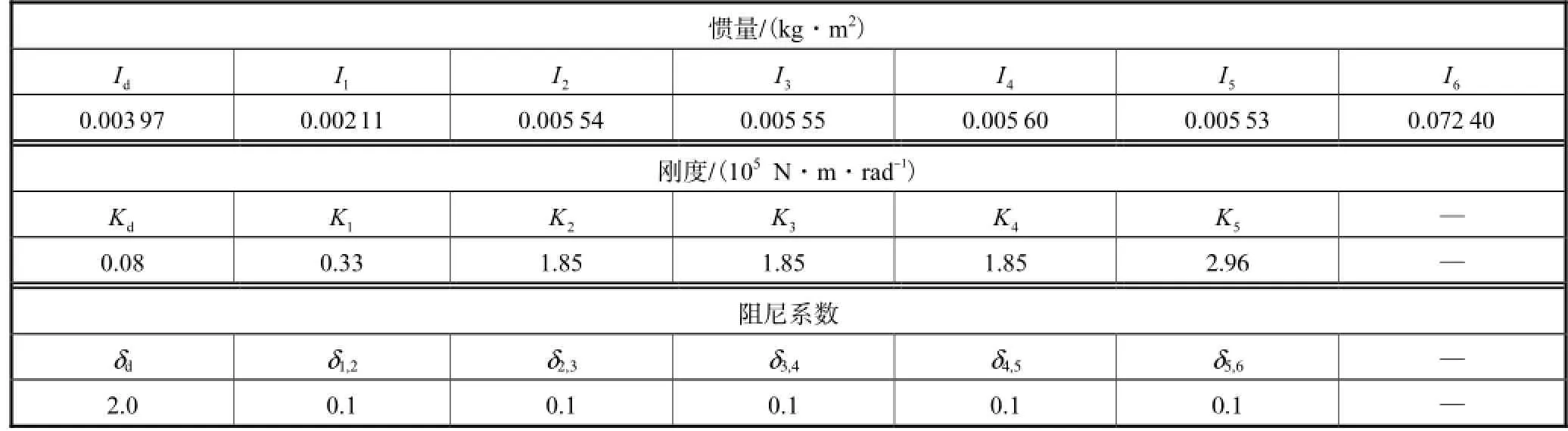
表1 发动机曲轴简化模型参数Tab.1 Engine crankshaft simplified model parameters

对此离散模型进行的扭转振动分析包括自由振动分析和强迫振动分析．首先，自由振动分析可以确定系统的自振频率和临界转速(共振转速)，是后文进行强迫振动和扭振减振器分析的依据．通过计算，扭振减振器惯量比为1.87，定调比为0.63，发动机不装配减振器时轴系前2阶自振频率分别为w1=482.0×104rad/s和w=179.6×104rad/s ；装配减振器时的轴2系前2阶自振频率分别为w1=185.3×104rad/s 和w=149.2×104rad/s ，其振型如图4所示．

2

图4 轴系扭振自振频率和振型Fig.4 Model and frequency of crankshaft torsional vibration

由图4可以看出，发动机在装配扭振减振器后，系统的自振频率和振型都有所变化，但仍需计算不装配减振器时系统的自振频率，并通过式(9)来确定适合的减振器定调比；而加装减振器后系统的自振频率可以用来确定系统的临界转速．本文发动机作为扭振计算的工作转速范围为1,000～5,500,r/min，主要研究4～9谐次干扰力矩对轴系产生的共振，发动机在装配扭振减振器后，发动机将主要与轴系1阶频率发生扭转共振，可能出现的临界转速(共振转速)如表2所示．

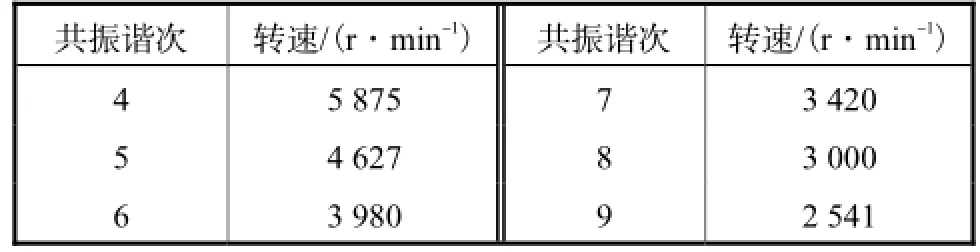
表2 轴系共振转速Tab.2 Shaft resonance rotation speed

对轴系的强迫振动分析，可以在计算中加入该谐次的简谐力矩矩阵，即可计算出该谐次下的强迫振动振幅．图5对比了发动机在不装配和装配扭振减振器的情况下曲轴自由端强迫振动的振幅．

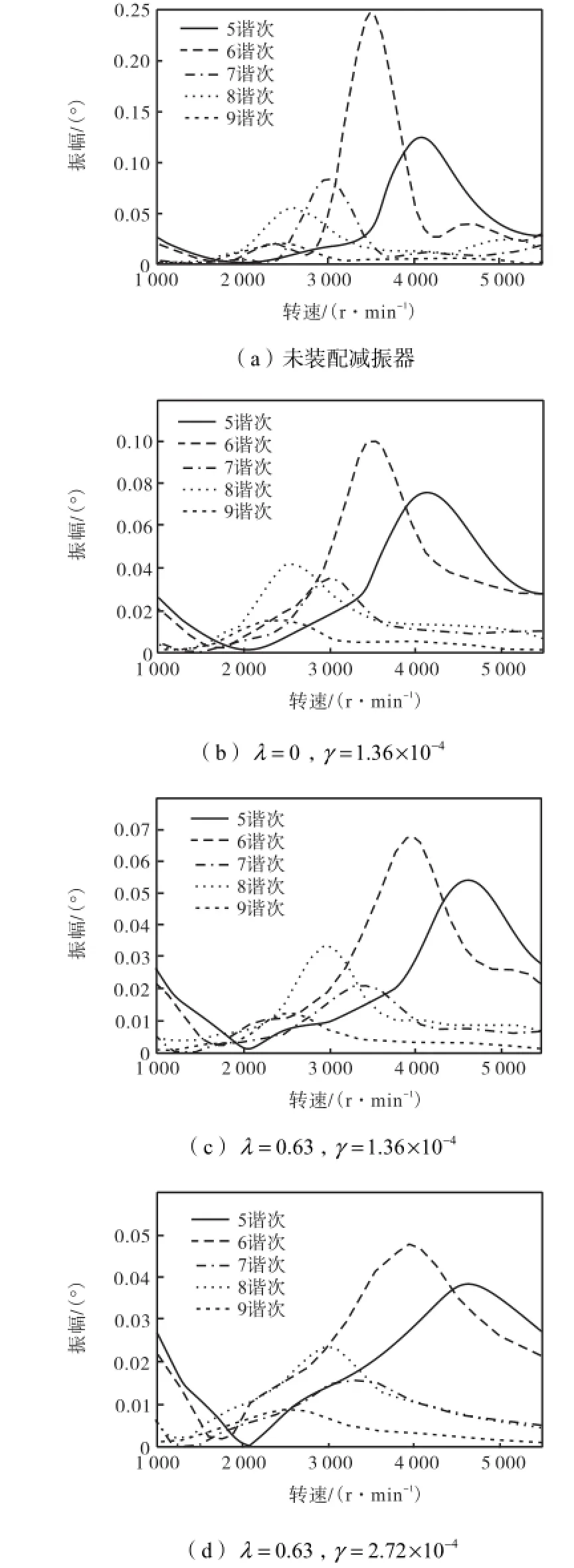
图5 发动机曲轴自由端强迫振动的振幅Fig.5 Forced vibration magnitude of crankshaft system free end

由图5(a)可知，发动机在未装配减振器时各谐次干扰力矩都会在其对应临界转速下达到最大扭转振幅值，如6谐次在3,500,r/min下振幅最大，达到0.247,6,°．从图5(a)、5(c)可看出，发动机在装配定值定调比、阻尼扭振减振器后，各谐次干扰力矩的临界转速(共振转速)都有所变化，如4谐次临界转速就超出了发动机工作转速范围，可以不予考虑．这与前文中提到的加装减振器后轴系的自振频率产生变化的情况相吻合．并且从图5(a)、5(d)可以看出扭振定调比的改变才是临界转速变化的主要原因，阻尼的主要作用是降低共振振幅，所以在计算轴系临界转速前确定扭振减振器的定调比是十分必要的．

3.2 轴系变阻尼扭振减振器分析

3.2.1 变阻尼扭振减振器各临界转速下最佳阻尼值

由图5可知，定值阻尼扭振减振器只能对某一谐次(如6谐次)干扰力矩在其对应临界转速下有较好的减振效果，而对其他谐次和临界转速的减振效果并不理想．所以，需要对扭振减振器做进一步分析，计算出扭振减振器在各临界转速下产生最佳减振效果时的阻尼值，称为最佳阻尼值，如图6所示.

图6 发动机各临界转速下最佳阻尼值Fig.6 Optimum damping value under the shaft critical rotation speed

3.2.2 变阻尼扭振减振器减振效果

图7为加装变阻尼扭振减振器后轴系自由端各谐次振幅曲线，从图中可看出，加装变阻尼扭振减振器后，系统的临界转速较之未加装扭振减振器发生了变化，更重要的是，当扭振减振器在各临界转速下取最佳阻尼值时，自由端扭转振幅均有明显的降低．

图7 加装变阻尼扭振减振器后轴系自由端强迫振动的振幅Fig.7 Forced vibration magnitude of crankshaft system free end with variable damping torsional vibration damper

表3为发动机在无减振器、加装定阻尼扭振减振器和变阻尼扭振减振器后，各谐次临界转速和扭振振幅对比．从表中可看出匹配定阻尼扭振减振器的曲轴系将5谐次振幅从0.124,8,°降到0.054,3,°，降低了56.25%；6谐次从0.247,5,°降到0.067,7,°，降低了72.65%．文本所匹配的变阻尼扭振减振器将5谐次降低到0.025,9,°，降低了79.25%；6谐次降低到0.034,0,°，降低了86.26%，并且发动机在工作转速范围内各谐次扭转振幅之和均达到0.15,°以下，改善了发动机的扭转振动特性．

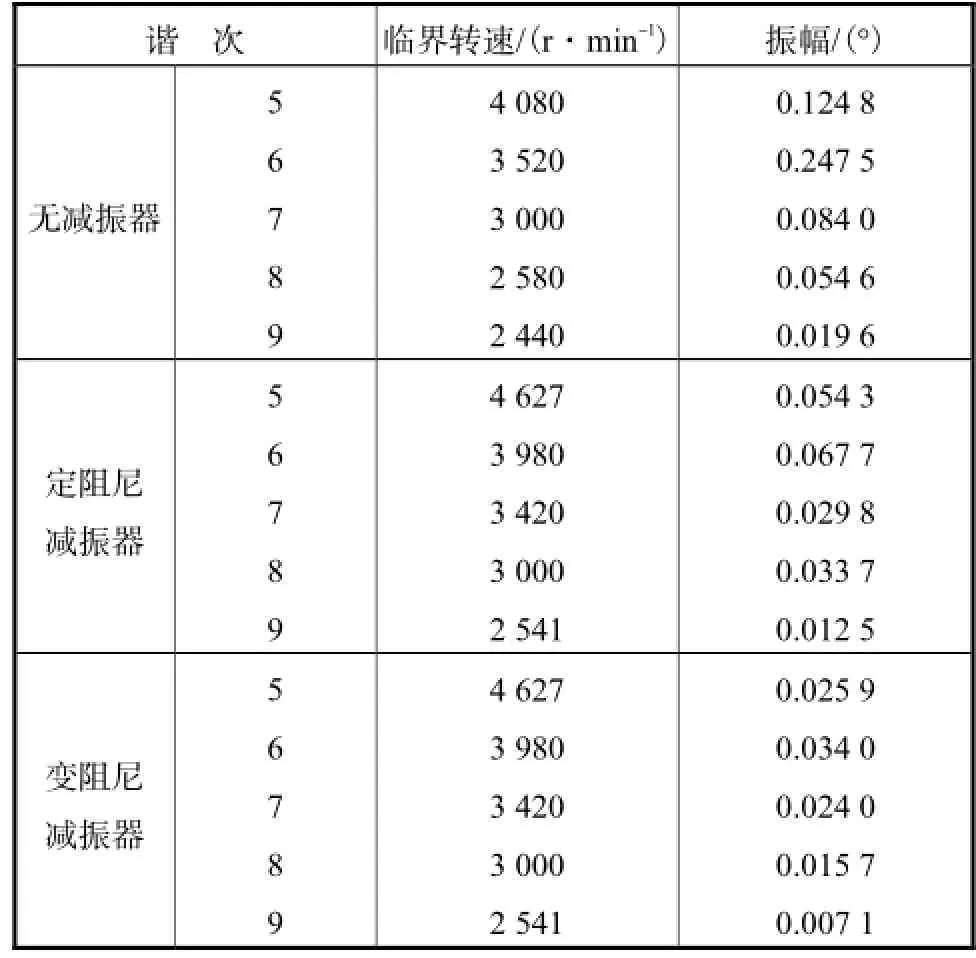
表3 减振结果对比Tab.3 Comparison of damping results

4 结 论

(1) 发动机在装配扭振减振器后，系统的自振频率和振型都有所变化，但还是需要计算出不装配减振器时系统自振频率来确定适合的减振器定调比；而加装减振器后系统的自振频率可以用来确定系统的临界转速．

(2) 发动机在加装变阻尼扭振减振器后，轴系临界转速将产生变化，并且可以知道其定调比的改变才是临界转速变化的主要原因，而阻尼的主要作用是降低共振振幅，对临界转速的影响不大．所以在计算轴系临界转速前需先确定扭振减振器的定调比．

(3) 发动机在装配变阻尼扭振减振器后，当减振器在各临界转速下取最佳阻尼值时，其各谐次减振效果非常明显，5谐次降低了79.25%，6谐次降低了86.26%，7谐次降低了71.43%，并且发动机在工作转速范围内各谐次扭转振幅之和均达到0.15°以下，改善了发动机的扭转振动特性．

［1］ 汪长民，杨继贤，孙业保，等. 车辆发动机动力学[M]. 北京：国防工业出版社，1983.

Wang Changmin，Yang Jixian，Sun Yebao，et al. Dynamics of Vehicle Engine[M]. Beijing：National Defence Industry Press，1983(in Chinese).

［2］ 宋希庚. 内燃机轴系扭转轴向耦合振动[D]. 大连：大连理工大学机械工程学院，1988.

Song Xigeng. Coupled Torsional and Axial Vibration of Internal Combustion Engine[D]. Dalian：School of Mechanical Engineering，Dalian University of Technology，1988(in Chinese).

［3］ 阎家宾. 发动机曲轴扭转振动的减振器[J]. 世界橡胶工业，1998，25(4)：26-30.

Yan Jiabin. Engine crankshaft torsional vibration damper [J]. World Rubber Industry，1998，25(4)：26-30(in Chinese).

［4］ 刘圣田，吕振华，邵 成，等. 双质量飞轮式扭振减振器[J]. 汽车技术，1997(1)：23-27.

Liu Shengtian，Lü Zhenhua，Shao Cheng，et al. Double mass flywheel type torsional vibration damper[J]. Automobile Technology，1997(1)：23-27(in Chinese).

［5］ Homik W. Damping of torsional vibrations of ship engine crankshafts—General selection methods of viscous vibration damper[J]. Polish Maritime Research，2011，18(3)：43-47.

［6］ Östman Fredrik，Toivonen H T. Torsional system parameter identification of internal combustion engines under normal operation[J]. Mechanical Systems and Signal Processing，2011，25(4)：1146-1158.

［7］ Hu Jianjun，Qin Datong，Zhao Yusheng，et al. Study on natural torsional vibration characteristics of dual mass-flywheel radial spring type torsional vibration damper[C]// SAE Paper. Detroit，MI，USA，2009：2009-01-2062.

［8］ 苏 芳，马建敏，刘 颖. 柔性联轴器对振动系统响应的影响[J]. 噪声与振动控制，2012(1)：163-166.

Su Fang，Ma Jianmin，Liu Ying. Effect of flexible couplings on response of a vibration system[J]. Noise and Vibration Control，2012(1)：163-166(in Chinese).

［9］ 贾启芬，刘习军. 机械与结构振动[M]. 天津：天津大学出版社，2007.

Jia Qifen，Liu Xijun. Mechanical and Structural Vibration[M]. Tianjin：Tianjin University Press，2007(in Chinese).

［10］ 李 梅. 发动机曲轴系动力学分析与动态性能优化[D]. 上海：上海交通大学机械工程学院，2009.

Li Mei. Crankshaft Kinetics Analysis and Dynamic Performance Optimization[D]. Shanghai：School of Mechanical Engineering，Shanghai Jiao Tong University，2009(in Chinese).

(责任编辑：金顺爱)

Torsional Vibration Reduction Analysis of Variable Damping Torsional Vibration Damper for Engine Crankshaft

Shu Gequn，Wang Bin，Liang Xingyu
(School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

Taking the crankshaft torsional vibration of engines as research object，we analyzed the effect of variation of damping ratio parameters of torsional vibration damper on the amplitude amplification coefficient of crankshaft torsional vibration. The design of variable damping torsional vibration damper was also carried out in this paper. The results show that after the variable damping torsional vibration damper is installed，both the natural frequency and critical rotation speed of the system increase. When the optimal damping value is selected for every critical rotation speed of the variable damping torsional vibration damper，it will lead to an obvious reduction in torsional amplitude of different orders at crankshaft system free end，which improves the torsional vibration features of the engine，and indicates that it is effective to depress the torsional vibration by means of using variable damping torsional vibration damper.

variable damping；torsional vibration damper；crankshaft torsional vibration；forced vibration

TK402

A

0493-2137(2015)01-0019-06

10.11784/tdxbz201307059

2013-07-29；

2013-08-26.

国家高技术研究发展计划(863计划)资助项目(2012AA111702)．

舒歌群（1964— ），男，教授，sgq@tju.edu.cn.

梁兴雨，lxy@tju.edu.cn.

时间：2014-01-06.

http：//www.cnki.net/kcms/doi/10.11784/tdxbz201307059.html.