基于ARIMA的电力视频流量分析和预测
崔振辉,李林川,赵承利,杨 挺
基于ARIMA的电力视频流量分析和预测
崔振辉1,2,李林川1,赵承利3,杨 挺1
(1. 天津大学智能电网教育部重点实验室,天津 300072;
2. 国网天津市电力公司,天津 300010;3. 天津航海仪器研究所,天津 300131)
针对电力视频业务的流量特性,提出一种基于差分自回归移动平均(ARIMA)模型的电力视频业务流量分析和预测方法.首先利用差分法对视频流量数据进行平稳化处理,然后依据数据序列的自相关函数和偏自相关函数确定模型参数,从而建立能够有效预测电力视频业务流量的分析模型.仿真实验表明,该方法充分考虑了电力视频业务流量的自相似性、周期性、突发性及趋势性等特点,有效提高了流量预测拟合的精度.
电力视频业务;流量分析;ARIMA;自相似
随着网络技术的不断发展,用户实时性、互动性需求不断增加,视频业务逐渐成为现代网络通信的重要组成部分,应用范围越来越广泛,视频业务流量的分析与预测也具有越来越重要的意义.
在电力生产领域,随着智能电网建设的不断深入,现代电网信息化、数字化、自动化、互动化的特征日益凸显[1-2],变电站远程遥视、设备在线监测、网络视频会议等视频业务[3-4]逐渐成为电力生产、企业运营中的必要组成部分.视频业务流量的特点是高带宽需求和严格的网络低时延保障,随着不断增多的视频流注入到电力通信网络,电力通信网络的流量属性发生显著变化.研究建立精确的电力视频流量分析和预测方法,有助于网络流量的分析和预测,对提升通信传输性能和效率、保障电力视频业务稳定性及可靠性具有关键意义.
研究表明:电力视频业务流量具有多尺度特性(自相似和短相关),同时还具有突发特性.传统的泊松模型、马尔可夫模型、回归模型(AR模型、MA模型、ARMA模型)只具有短相关性,难以描述电力视频流量的突发性和自相似特性.差分自回归移动平均(autoregressive integrated moving average,ARIMA)模型则是一种融合了时间序列分析和回归分析的优化时间预测模型,可以处理有季节性、周期性等趋势方面的非平稳序列,并且在对网络行为预测和控制方面具有模型及参数估计简单、建模效率高等特点[5-8].本文提出一种基于ARIMA的电力视频业务流量分析和预测方法,仿真实验表明,该方法充分考虑了电力视频业务流量的自相似性、周期性、突发性及趋势性等特点,有效提高了流量预测拟合的精度.
1 通信流量特性
表征通信流量特性的重要特征量包括尺度特性(如自相似性[9])和多尺度特性(如长相关性、多重分形性),随着流量分析和研究的发展,周期性、混沌性等特性也逐渐受到重视.
1.1 自相似性和长相关性
如果某种结构或过程的特征从不同的空间尺度或时间尺度来看都是相似的,或者某系统或结构的局域性质或局域结构与整体相似,则认为该系统具有自相似性.其定义为:一个连续时间的随机过程Y(t)={Y(t),t∈T},若Y(t)在不同时间尺度上的统计特性不变,即Y(t)满足:Y(t)=α-HYαt,∀α>0,0≤H<1. 其中H称为Hurst参数,一般而言,H值越大,表示自相似程度越高,突发性也越高.
此外,网络流量还具有长相关性,主要指自相似过程中的持续现象,即突发特性在所有时间尺度上都存在的现象.长相关性侧重于业务量的统计特性,而自相似性主要指离散或连续过程有限维分布的尺度不变特性,偏重于数学表述上,因此长相关性和自相似性是不等价的.电力视频业务普遍存在自相似和长相关特性,业务流量在不同的时间周期内具有相似性,在大范围的时间尺度上具有突发性,表现为明显的高业务量时段和空闲时段.
1.2 多重分形性
随着网络流量复杂性的增加,研究发现自相似性已不能满足描述复杂流量的需求,进而采用多重分形测度或维数来描述流量特性.多重分形是指网络流量分布不均匀,在不同时间尺度下的流量表现出明显的差异性.Riedi等[10]通过对TCP流量的数值分析,发现网络流量在较大时间尺度上表现为长相关性,而在较小的时间尺度上突发性和复杂性更为突出.多重分形性延伸和细化了网络流量中的自相似行为,体现了不同时间尺度的流量特点,通过更加灵活的方式描述局部时间内的不规则现象.近年来,电力通信网络规模迅速扩展,视屏业务应用范围越来越广泛,视频业务流量在时间和空间上的差异性越来越明显.研究电力视频业务流量的多重分形特性,建立有效的分析预测模型,对整体网络的设计和流量管理具有重要的意义.
1.3 周期性
网络流量的周期性是指流量随时间的变化而表现出来固定的变化规律.造成流量周期性的原因主要有数据的周期间隔采集、通信业务的固有属性等因素.由于电力生产、经营业务具有固定的周期,例如设备在线监测、营业厅及施工现场视频采集、网络视频会议等工作内容,导致电力视频业务具有明显的周期性.
2 基于ARIMA的建模分析
2.1 ARIMA模型描述
ARIMA模型是由Box等[11]提出的一种时间序列预测方法,是差分运算与ARMA模型的结合,任何非平稳序列只要能够实现差分后平稳,即可对差分后的序列进行ARIMA模型建模.
设Z=(Z1,Z2,Z3,…,Zn-1,Zn)为等时间间隔1,2,3,…,n-1,n采集到的VoIP流量序列,αt为流量误差序列,ARIMA模型可表示为

式中:B为后移算子;∇d为向后差分算子;d为差分阶数;假定∇=1-B ,则有
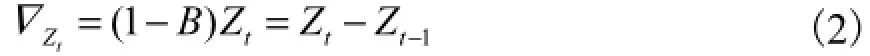
2.2 建模分析
基于ARIMA模型进行建模的过程中[12-16],首先需要对电力视频业务流量中的非平稳时间序列通过差分法进行平稳化处理,然后再按照平稳时间序列模型进行性能分析.其次是模型的定阶,一般ARIMA(,,)pdq模型的定阶方法是依据自相关函数ACF和偏自相关函数PACF的绝对值,并通过图形对比分析确定参数p、d、q的值.
首先进行平稳化处理,差分算子可以表示为
式中:Δ为差分算子;Δd=Δd-1(x-x)=
p取值通过相关函数确定;d的取值范围为{0,1,2},一般取为1;q取值通过偏自相关函数确定.一般利用自协方差函数的自相关函数作为自相关性的评价标准.
设自协方差函数为R(h),针对平稳序列{yt},则有
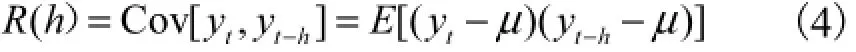
式中h为任意整数.
将自协方差函数进行标准化,得到自相关函数

偏自相关函数的估计kkϕ计算公式为
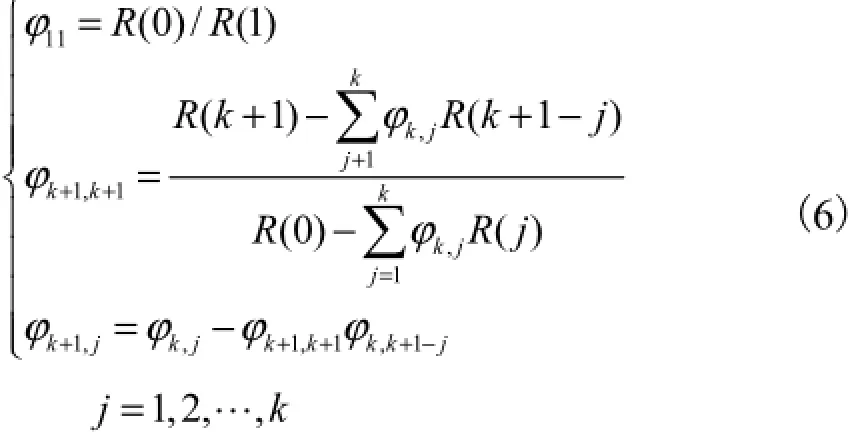
通过自相关及偏自相关函数可以绘制对应的函数图,进而可以分析出时间序列各阶滞后的自相关和偏自相关函数值,同时计算出置信区间.
本文采用的定阶方法主要通过自相关函数{ρk}和偏自相关函数{ϕk,k}的结尾性判断模型的阶数.对于平稳时间序列{yt},当p=0时,即模型为MA(q)模型,则模型的自相关函数{ρk}在q步截尾;当q=0时,模型即为AR(p)模型,此时模型的偏自相关函数在p步截尾.因此对于自相关函数和偏自相关函数有3种情况:①如果样本的自相关函数{ρk}在q步截尾,则可以判定p=0,模型为MA(q);②如果样本的偏自相关函数{ϕk,k}在p步截尾,则可以判定q=0,模型为AR(p);③如果样本的自相关函数{ρk}和样本的偏自相关函数{ϕk,k}均拖尾,则可判定为ARMA(p,q)模型.综上所述,基于ARIMA的建模流程如图1所示.
2.3 残差检验和预测
模型建立后,要对模型的适应性进行检验.模型的适应性是指模型已经完全或基本上反映了系统的动态性,从而模型中的残差tε是白噪声序列,即模型的适应性检验实际上是tε的独立性检验.目前的残差检验方法主要有两种:Ljung-Box检验法与判读残差的自相关和偏自相关函数图.
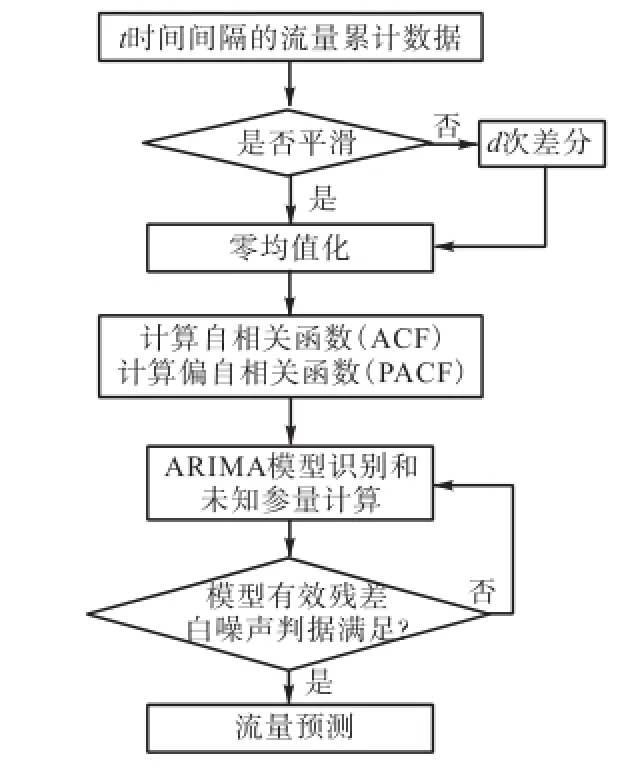
图1 基于ARIMA的建模流程Fig.1 Modeling process based on ARIMA
1) Ljung-Box检验法
原假设:残差序列为白噪声序列,即

计算LB(Ljung-Box)统计量为

若拒绝原假设,表明残差序列中还残留有相关信息,拟合模型不显著;若没有拒绝原假设,则表明拟合显著.
2) 判读残差的自相关和偏自相关函数图
同时还可以通过判读残差的自相关和偏自相关函数图来进行白噪声检验.若残差的自相关函数和偏自相关函数值均落在95%的置信区间内,则认为残差序列为白噪声序列.
残差检验合格的流量模型就可以用来对电力视频业务流量进行分析和预测,有效掌握近期网络流量走向,从而有针对性地预留网络资源、节约带宽、提高利用效率.在面对突发数据时,既保证业务的带宽需求,又防止由于网络阻塞造成的不必要损失,同时也可以采取合理的丢弃算法或措施,舍弃次要数据,保障关键业务数据的传输质量.
3 针对电力视频流量的分析预测模型
3.1 数据承载业务分析
视频业务是近几年在电力生产中出现的新型业务,在电力视频监控和企业信息化运营方面起着重要的作用.现阶段的电力视频业务主要包括变电站的远程遥视、设备状态的在线监测和网络视频会议等内容,数据源为采用H.320、H.264技术的电视会议系统和视频点播以及低品质的视频监控.
3.2 流量数据的采集与预处理
本文提取承载视频监控业务的SDH设备数据流量,时间间隔为1,min/次,周期为24,h(即为一工作日),共计1,440个流量数据,如图2所示,流量在垂直方向存在剧烈跳动,呈现非平稳特性.
进一步分析得出原始数据序列的自相关函数图和偏自相关函数图,如图3和图4所示.可以看出,原始数据序列存在着趋势性、周期性,自相关函数图也表现出趋势性,有拖尾趋势,同时也可以发现其周期性.
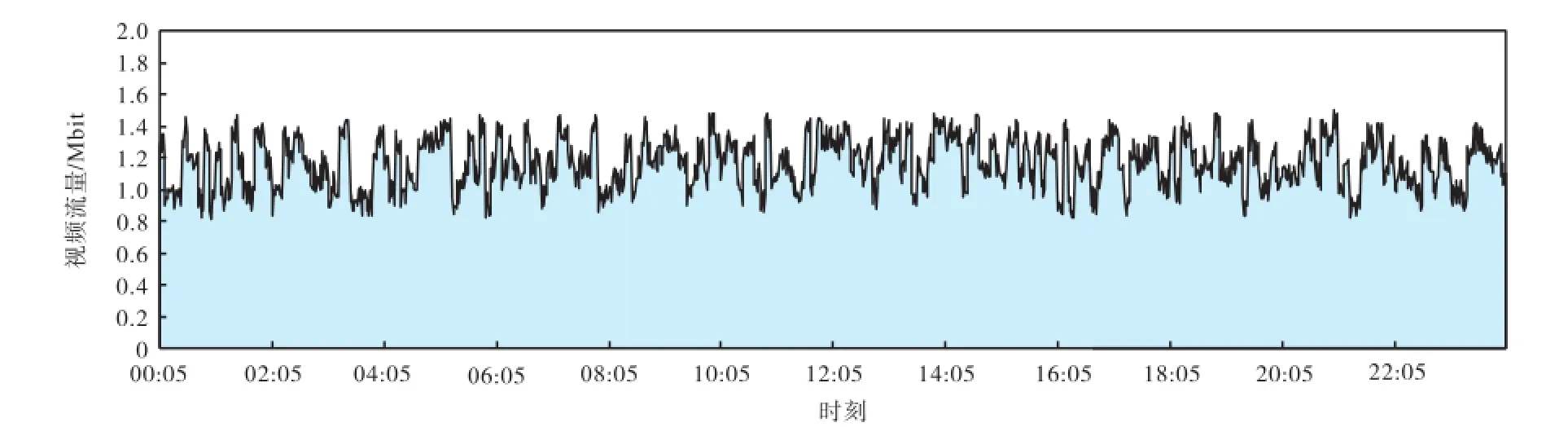
图2 电力视频流量数据Fig.2 Power video traffic data
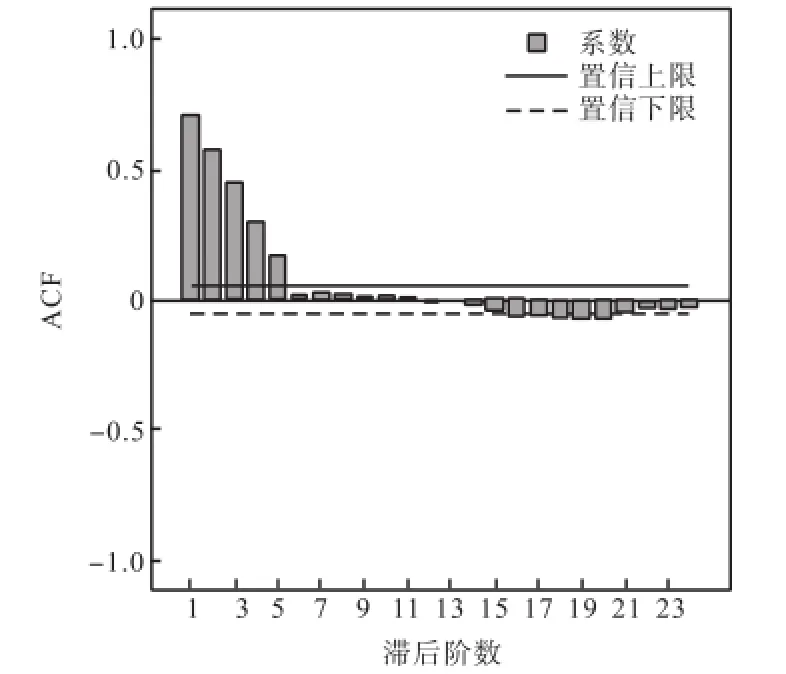
图3 自相关函数图Fig.3 Autocorrelation function
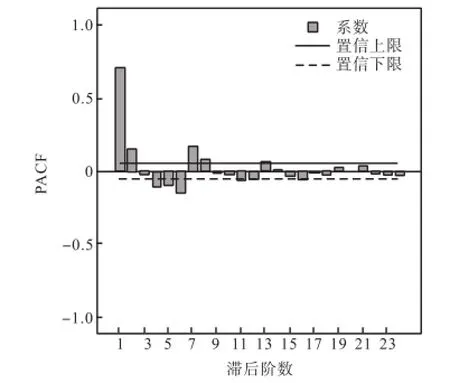
图4 偏自相关函数图Fig.4 Partial autocorrelation function
从偏自相关函数图来看,除1阶函数值之外,2阶、4阶、5阶、6阶、7阶、8阶、11阶、13阶均不为0,说明序列中除趋势性外还存在着某些特殊的相关性.
为消除序列中的趋势性,对该数据序列进行1阶逐级差分处理,处理后数据的自相关函数图和偏相关函数图如图5和图6所示.分析可知,1阶差分后自相关函数图中只有1阶和6阶显著不为0,其他各阶均趋于0.偏自相关函数也整体呈现出拖尾式,只有1阶和6阶、7阶显著不为0,说明序列中的趋势性已经基本消除,符合建模要求.
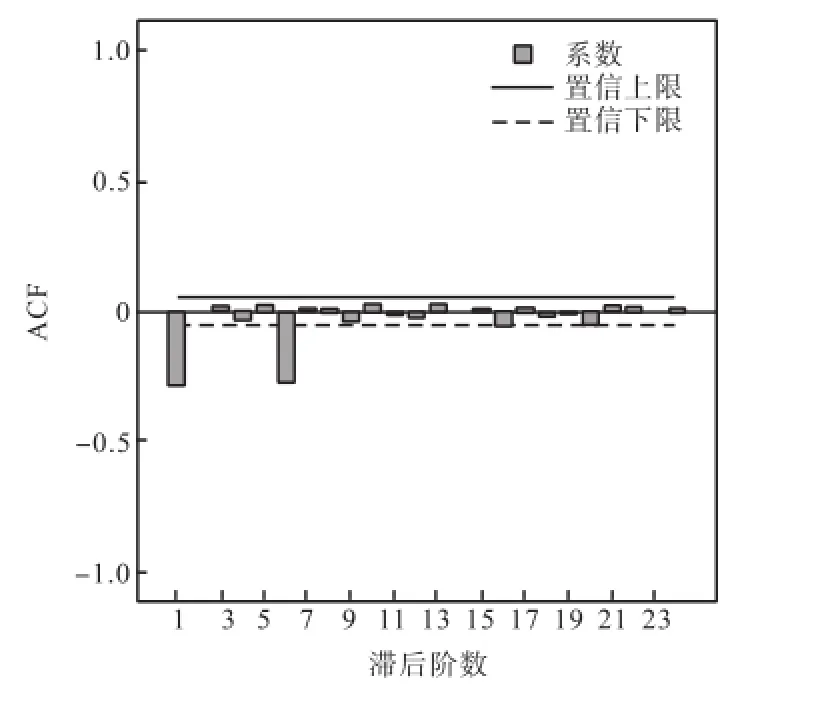
图5 1阶差分后的自相关函数图Fig.5 Autocorrelation function after first difference

图6 1阶差分后的偏相关函数图Fig.6 Partial autocorrelation function after first difference
3.3 模型参数的确立
分析1阶差分后序列的自相关函数图和偏自相关函数图可知,自相关函数图整体呈现拖尾的趋势,1阶以后的函数值明显趋于0,但是在6阶处又出现函数值显著不为0的情况;偏自相关函数图整体呈现拖尾的趋势,其中1阶、6阶、12阶处的函数值显著不为0.因此考虑两种情况,一种是简单考虑自相关函数图,令6q=,即模型为MA(6);另一种是考虑偏自相关函数中体现出的周期性,周期为6.
在数据处理的过程中,仅进行了1阶逐级差分,所以d和D季节差分次数分别取1和0.从1阶差分后的自相关函数图看,1阶以后的函数值明显趋近为0,因此q取值为1;同时,在第1个周期结束、第2个周期开始的6阶,可以看出函数值不为0,因此Q(季节性移动平均阶数)取值为1.通过偏自相关函数图可以看出,第1个周期阶内,2阶以后的函数值明显趋于0,所以p取2;而在第2个周期的2阶处,函数也显著不为0,在第3个周期阶的2阶处处于置信区间内,但是1阶仍显著不为0,所以P(季节性自回归阶数)取1或2.
通过上述分析确定模型的参数p、d、q、P、D、Q分别为1、1、2、1、0、1或1、1、2、2、0、1,周期为6.
3.4 建立模型
通过SPSS软件,分别对ARIMA(0,1,6)(0,0,0)、ARIMA(1,1,2)(1,0,1)6和ARIMA(1,1,2)(2,0,1)6进行建模,3个模型都满足ARIMA模型的平稳条件和可逆条件,模型设定合理.但在残差检验过程中发现ARIMA(1,1,2)(1,0,1)6和ARIMA(1,1,2)(2,0,1)6不能满足残差序列白噪声的检验.本文采用Ljung-Box检验,检验结果如表1所示.

表1 各模型Ljung-Box检验结果比较Tab.1 Comparison of Ljung-Box test results
要求Ljung-Box检验统计量离散度大于0.05,因此选择ARIMA(0,1,6)(0,0,0)进行建模,得到数据如表2所示.
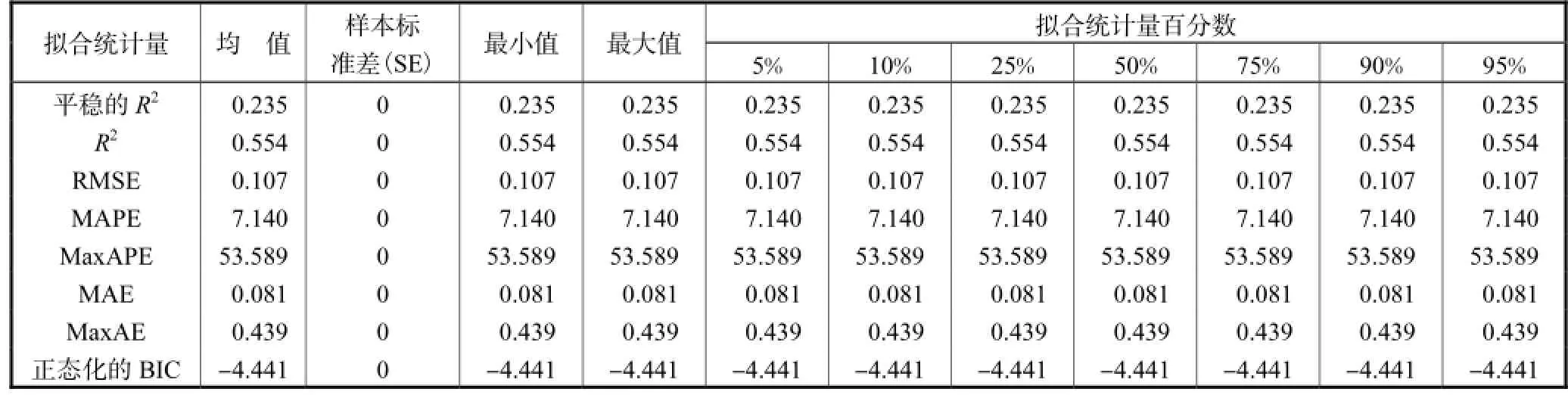
表2 ARIMA(0,1,6)(0,0,0)模型拟合Tab.2 Fitting of ARIMA(0,1,6)(0,0,0)
表2给出了模型的8个拟合优度指标的均值、最小值、最大值和百分数,从2个2R值来看,ARIMA (0,1,6)(0,0,0)拟合情况良好.
表3给出了ARIMA(0,1,6)(0,0,0)模型的参数估计值,该模型主要是一阶差分后的MA(6),其显著性水平依次是0、0.295、0.418、0.002、0、0,基本都比较显著,因此选择ARIMA(0,1,6)(0,0,0)模型进行预测分析.

表3 ARIMA模型参数Tab.3 Model parameters of ARIMA
4 模型的检验及仿真分析
4.1 残差检验
对于模型的整体性效果,可以通过对残差序列的分析得出结论,如果序列的自相关和偏自相关函数值显著为0,同时该序列为随机序列,则该模型为一个理想模型.
本文所建模型残差序列的自相关函数图和偏自相关函数图如图7所示,横轴为滞后阶数,纵轴为残差ACF和PACF函数值,图中2条横线中间表示95%置信区间.可以看出,自相关和偏自相关函数各阶函数值均处于随机区域,同时趋近于0,具有典型的随机性,符合判定条件.

图7 残差序列的自相关和偏自相关函数图Fig.7 Autocorrelation and partial autocorrelation function of residual sequence
同时,Ljung-Box检验结果如图8所示,可以看出,所有的离散度都在0.05以上,因此残差是白噪声,与最初假设相符.
4.2 模型预测分析
在建立模型时,把拟合数据保存下来,用于模型的拟合程度分析,采用ARIMA(0,1,6)(0,0,0)模型,即
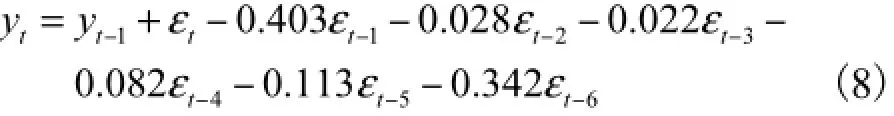
式中ty为视频流量经数据初步处理和分数差分后的时间序列.
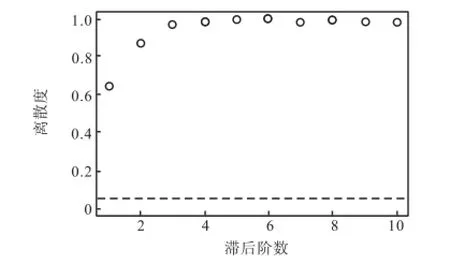
图8 Ljung-Box检验结果Fig.8 Ljung-Box test results
该模型观测值与拟合值的拟合序列如图9所示,图中灰线为观测值,即经分数差分后时间序列的实际值,黑色为模型的拟合值,从图9中可以看出,该模型对数据序列具有较好的拟合效果.

图9 电力通信网视频业务流量拟合分析Fig.9 Traffic fitting analysis of the power video
5 结 语
电力视频流量的建模与预测对提高电力视频业务的传输效率和提升网络资源利用效率具有重要意义.ARIMA模型对非平稳序列具有良好的处理效果,同时模型及参数估计简单、建模效率高,本文提出一种基于ARIMA的电力视频业务流量分析和预测方法,详细介绍了建模的分析过程和步骤,并采用实际电力视频业务数据进行分析和预测拟合仿真.仿真实验表明,该方法充分考虑了电力视频业务流量的自相似性、周期性、突发性及趋势性等特点,有效提高了流量预测拟合的精度,具备较高的理论意义和应用价值.
参考文献:
[1] 樊剑辉. 智能化配电网管理系统通信模式的研究[J].电力系统通信,2009,30(205):20-25.
Fan Jianhui. Study on communication mode of smart distribution network management system[J]. Telecommunications for Electric Power System,2009,30(205):20-25(in Chinese).
[2] 李文伟. 电力数据通信网的业务流量分析[D]. 上海:上海交通大学信息安全工程学院,2007.
Li Wenwei. The Traffic Analysis of Power Data Communicational Network Service[D]. Shanghai:College of Information Security,Shanghai Jiao Tong University,2007(in Chinese).
[3] 王 斌,楼颖稚. 视频监控的发展及在电力系统中的应用[J]. 电力系统通信,2004,25(11):57-60.
Wang Bin,Lou Yingzhi. Development and application of the video supervision in the electric power system[J]. Telecommunications for Electric Power System,2004,25(11):57-60(in Chinese).
[4] Yoo S J. Efficient traffic prediction scheme for real-time VBR MPEG video transmission over high-speed networks[J]. IEEE Trans on Broadcasting,2002,48(1):10-18.
[5] 董 燕,孙恩昌,孙艳华,等. 基于傅里叶模型的最佳网络流量预测[J]. 计算机应用研究,2010(4):1419-1421.
Dong Yan,Sun Enchang,Sun Yanhua,et al. Optimum prediction of network traffic based on Fourier model[J]. Application Research of Computers,2010(4):1419-1421(in Chinese).
[6] 唐 斐. 基于分形的网络流量模型的分析与研究[D].北京:北京邮电大学信息与通信工程学院,2008.
Tang Fei. Analysis and Research of Network Traffic Model Based on Fractal Theory[D]. Beijing:School of Information and Communication Engineering,Beijing University of Posts and Telecommunications,2008(in Chinese).
[7] Tsybakov B. Traffic Modeling and Analysis[D]. New York:Dept of Electrical Computer and Systems Eng,Rensselaer Polytechnic Inst,1998.
[8] Pang Mingbao,Zhao Xinping. Traffic flow prediction of chaos time series by using subtractive clustering for fuzzy neural network modeling[C]// 2nd International Symposium Intelligent Information Technology Application. Shanghai,China,2008:23-27.
[9] Mandelbrot B. Self-similar error clusters in communication systems and the concept of conditional stationarity[J]. IEEE Trans on Communication Technology,1965,13(1):71-90.
[10] Riedi R H,Véhel J L. TCP Traffic is Multifractal:A Numerical Study[R]. Houston:Rice University,1997.
[11] Box G E P,Jenkins G M,Reinsel G C. Time Series Analysis:Forecasting and Control[M]. 3rd ed. Englewood Cliffs:Prentice-Hall,1994.
[12] 金 旗,裴昌幸,朱畅华. ARIMA模型法分析网络流量[J]. 西安电子科技大学学报,2003,30(1):6-10.
Jin Qi,Pei Changxing,Zhu Changhua. ARIMA analysis method in network traffic[J]. Journal of Xidian University,2003,30(1):6-10(in Chinese).
[13] Babu C N,Reddy B E. Predictive data mining on average global temperature using variants of ARIMA models[C]//2012 International Conference on Advances in Engineering,Science and Management. Nagapattinam Tamil Nadu,India,2012:256-260.
[14] Amin A,Colman A,Grunske L. An approach to forecasting QoS attributes of web services based on ARIMA and GARCH models[C]//2012 IEEE 19th International Conference on Web Services. Honolulu,HI,USA 2012:74-81.
[15] Corradi M,Garroppo R G,Giordano S,et al. Analysis of f-ARIMA processes in the modeling of broadband traffic[C]// IEEE International Conference on Communications. Helsinki,Finland,2001:964-968.
[16] Nagarajan K. Fractional ARIMA Process and Its Applications in Network Traffic Modeling[EB/OL]. http:// citeseer. nj. nec. com/332607. html,1998-08.
(责任编辑:孙立华)
Traffic Analysis and Forecasting of Power Video Services Based on ARIMA Model
Cui Zhenhui1,2,Li Linchuan1,Zhao Chengli3,Yang Ting1
(1. Key Laboratory of Smart Grid of Ministry of Education,Tianjin University,Tianjin 300072,China;2. State Grid Tianjin Electric Power Company,Tianjin 300010,China;3. Tianjin Navigation Instruments Research Institute,Tianjin 300131,China)
Given the characteristics of power video services,a power video traffic analysis and prediction method was proposed based on the autoregressive integrated moving average(ARIMA)model. First,the video traffic data went through the smoothing process through different methods. Then the model parameters were determined by the autocorrelation function and partial autocorrelation function of the data sequence. Thus an effective prediction power video traffic analysis model was established. Simulation results show that the model can meet the characteristics of self-similarity,periodicity,suddenness and trends in power video traffic,and has effectively improved the fitting precision of traffic projections.
power video service;traffic analysis;autoregressive integrated moving average(ARIMA);selfsimilarity
TM734
A
0493-2137(2015)01-0049-07
10.11784/tdxbz201309034
2013-09-10;
2013-11-22.
国家自然科学基金资助项目(61172014);国家国际科技合作与交流专项资助项目(2013DFA11040);天津市自然科学基金重点资助项目(12JCZDJC21300).
崔振辉(1982— ),男,博士研究生,工程师,xiaocui_82@126.com.
杨 挺,yangting@tju.edu.cn.
时间:2014-03-25.
http://www.cnki.net/kcms/doi/10.11784/tdxbz201309034.html.

