异质Stackelberg寡头竞争下创新产品技术许可策略研究
王 静,包振华
(辽宁师范大学 数学学院,辽宁 大连 116029)
异质Stackelberg寡头竞争下创新产品技术许可策略研究
王 静,包振华
(辽宁师范大学 数学学院,辽宁 大连 116029)
基于异质产品Stackelberg寡头竞争模型, 建立了拥有新产品创新技术在位厂商与潜在竞争对手间的技术许可博弈模型. 模型中假设潜在竞争对手可以接受许可,也可通过自我研发创新技术进入市场参与竞争. 根据潜在竞争对手研发成本的高低,研究了创新厂商的最优两部制收费策略.研究结果表明:潜在竞争者总会接受创新技术许可,最优许可策略依赖于研发成本、市场参数以及产品的替代系数.
Stackelberg寡头模型;两部制收费;异质产品;研发成本
1 引 言
技术许可作为技术要素流动的主要形式,是技术发挥经济主导力量的有效途径.技术许可的核心问题之一是许可技术合约中价格条款的确定.通常,技术许可合约收费方式包括固定费用许可、纯产量提成许可和两部制收费三种, 其中两部制法是指同时包含固定费用和可变费用两种费用的许可方式.现实中,由于考虑到技术产业化过程具有一定的相关风险,技术许可的许可方和接受方往往采用两部制收费方式,即购买专利的厂商首先支付一定的入门费,然后按照实际产出支付可变费.Rostoker根据150家高新技术企业关于技术许可机制的一项实证研究发现, 约13%使用固定费许可,39%使用产量提成许可,46%使用两部制收费[1].
在理论研究中,产品市场的结构通常基于寡头垄断市场进行的.Wang研究了质量提高型内部创新者在产品市场从事Cournot竞争的许可决策问题,证明了提成许可优于固定费用许可[2];阎和朱构建了拥有质量提高型技术创新的外部创新者与Cournot双寡头垄断产品生产厂商间的技术许可博弈模型[3];李红珍等基于上游原料供应商具有重要市场势力以及下游同质产品Cournot产量竞争结构对创新许可决策博弈进行了研究[4];Wang和Yang则基于差异产品的Bertrand价格竞争研究了质量提高型内部创新者的技术许可问题[5];Filippini[6]以及Ferreira和Bode[7]则研究了Stackelberg领先结构下内部创新者的技术许可策略.
最近,Kitagawaa[8]等提出了一个新的创新技术许可决策模型,即假设拥有新产品创新技术的厂商使用两部制法许可创新技术.与以往文献不同,文中假设潜在竞争对手在不侵权的条件下可以自我研发该技术进入市场并生产不完美替代产品.由于在现实经济实践中,研发过程存在较大的不确定性且存在技术溢出效应,该文按照高研发成本及低研发成本两种情况给出Cournot寡头竞争模型的市场均衡分析. 本文在文献[8]的基础上, 基于Stackelberg产量竞争结构对该许可博弈模型进行研究.
2 模型建立
假设市场上有厂商1(领头厂商)和厂商2(追随厂商)两家企业,其中厂商1拥有生产某种新产品的创新技术,而厂商2没有此技术.厂商1可以将此创新技术许可给潜在的竞争对手2使用,两厂商间的许可博弈模型包括3个阶段:
阶段1 厂商1决定是否将创新技术许可给厂商2使用;
阶段2 若厂商1不许可,则厂商2可能采取两种策略:退出市场或自我研发该创新技术而进入市场,研发成本为J>0.若厂商1同意许可,厂商2也可能采取两种策略:同意或拒绝许可. 如果拒绝,厂商2可以选择退出市场或者自我研发新技术进入市场.
阶段3 若厂商2进入市场,它和厂商1关于新产品进行Stackelberg竞争;若2退出市场,则1成为新产品的垄断厂商.
假定厂商1采用两部制收费方式进行技术许可,即厂商2在接受技术转让后需要向厂商1支付固定费用F≥0以及单位产出费用r≥0,其中F独立于厂商2的产品产量,以下将此许可方式记为(r,F).尽管两家厂商使用相同的创新技术生产新产品,假设其生产的产品具有水平差异性,即市场的逆需求函数为
pi=θ-qi-aqj,i,j=1,2,i≠j,
其中pi为厂商i的产品价格,qi为厂商i的产品产量,a∈[0,1)表示两家厂商的产品差异性程度.当a→1时,表示两家厂商的产品差异性愈小;当a=0时,表示两家厂商的产品为独立性产品. 当厂商2接受厂商1的两部制收费(r,F),则厂商2应该支付给厂商1的费用为rq2+F.
为方便分析,采用以下几个假设条件:
假设1 两厂商采用新技术生产新产品的边际成本标准化为0;
假设2 当厂商2不在意是否进入市场时,假设其选择进入市场;
假设3 当厂商2不在意是否接受技术许可时,假设其接受许可;
假设4 当厂商1不在意是否将新技术许可给厂商2时,选择不许可.
零成本假设在本质上和线性成本技术是一致的,若考虑规模经济等非线性因素时这个假设则不成立.假设2的意思是,若进入市场与否对厂商2而言利润一致,则厂商2选择进入市场,假设3和4有类似的解释.
3 预备性引理
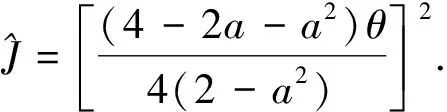
(1)

(2)
证明 首先考虑厂商2进入市场和厂商1关于产量进行Stackelberg竞争. 给定领头厂商1的产量q1的情况下,追随厂商2确定最优的最终产品产量q2使其利润最大化:
由最大化一阶条件,得追随厂商的相机行动规则为
(3)
领头厂商1预测到追随厂商2将根据式(3)选择最佳产量,所以直接将式(3)代入自己的利润函数,其问题为:
求解最大化一阶条件,得厂商1的最优产量为
(4)
将式(4)代入式(3)中,得厂商2的最优产量为
(5)
将式(4)和(5)分别代入厂商1和厂商2的利润函数中整理即得式(2).
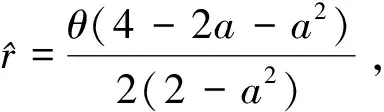
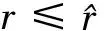
+F,
(6)
(7)

(8)
证明 类似于引理1的证明,当厂商1同意许可创新技术而厂商2接受许可时,在给定厂商1的产量q1的情况下,厂商2的问题变为
由最大化一阶条件,得厂商的相机行动规则为
(9)
厂商1预测到厂商2将根据式(9)选择最佳产量,其问题变为:
将式(9)代入上式并求解最大化一阶条件,得厂商1的最优产量为
(10)
将式(10)代入式(9)中,得厂商2的最优产量为
(11)
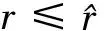
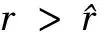
4 高研发成本下的均衡分析

(12)
对于领头厂商1而言,其目标是选择(r,F)使得Π1(r,F)最大化. 由式(6)和(12)知,固定费用F应该取为
(13)
将式(13)代入式(6)整理得
Π1(r,F)
(14)
其中k(a)=32-32a-8a2+12a3-a4. 易知式(14)分子的最大值点在
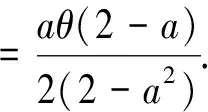
(15)

(16)
(17)
将式(15)和(16)代入式(7)知厂商2的均衡利润为零.
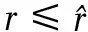

5 低研发成本下的均衡分析

(18)
现在考虑r的情况.厂商2接受许可的充要条件为). 由式(7)和式(18)知这等价于
+J.
(19)
注意到许可合同(0,J)显然满足条件式(19),由于J>0,因此
经简单的计算得知
Δ=θ2(4-2a-a2)2-16(2-a2)2J.
则式(18)意味着Δ≥0,因此由式(19)以及二次函数的性质知使得Fl(r)≥0的单位产出费用r应该满足
(20)
Π1(r,F)
+J.
(21)
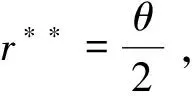

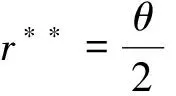
(22)
(23)
将r**和式(21)代入到式(7)中得厂商2的均衡利润为
(24)

+2J,
(25)
(26)
将前面的分析总结为定理2.
6 结 论
现有关于技术许可策略的文献绝大多数关注成本降低型创新技术或质量提高型技术,关于新产品创新的研究相对较少.对在位创新厂商在Stackelberg竞争框架下的两部制收费策略的优化进行了研究.与以往研究不同,在模型中假设潜在竞争对手可以通过自我研发新技术进入市场参与竞争.模型的主要特征在于新产品技术的研发成本,当研发成本过高时采用这种方式进入市场对于潜在竞争者来说是不可取的.通过考虑高研发成本和低研发成本两种情形,给出了两部制收费下的市场均衡分析.这些结论可以为企业的策略选择提供重要的理论参考依据.
[1]MROSTOKER.Asurveyofcorporatelicensing[J].TheJournalofLawandTechnology,1984,24( 2):59-92.
[2]XHWANG.FeeversusroyaltylicensinginaCournotduopolymodel[J].EconomicsLetters, 1998,60(1):55-62.
[3] 闫庆友, 朱丽丽. 古诺竞争条件下质量提高型技术许可策略研究[J].科技进步与对筞,2011,28(19):16-19.
[4] 郭红珍,黄文杰,张荣乾.上游市场结构与下游Cournot厂商创新者固定费用特许的互动研究[J].数量经济技术经济研究, 2005,20(10): 125-134.
[5]XHWANG,BZYANG.OnlicensingunderBertrandcompetition[J].AustralianEconomicPapers, 1999,38(2):106-19.
[6]LFILIPPINIi.LicensingcontractinaStackelbergmodel[J].TheManchesterSchool, 2005, 73(1):582- 598.
[7]FFERREIR,RBODE.Licensingendogenouscost-reductioninadifferentiatedStackelbergmodel[J].CommunicationsinNonlinearScienceandNumericalSimulation, 2013, 18(2):308-315.
[8]TKITAGAWA,YMASUDAB,MUMEZAWAC.Patentstrengthandoptimaltwo-parttarifflicensingwithapotentialrival[J].EconomicsLetters, 2014, 123(2): 227-231.
Study on Licensing Strategies of New Product Innovation in a Differentiated Stackelberg Duopoly
WANG Jing, BA Zheng-hua
(School of Mathematics,Liaoning Normal University,Dalian,Liaoning 116029, China)
Based on a differentiated Stackelberg duopoly, this paper established a licensing game model in which an incumbent innovator competing with a potential rival can develop the technology for the new product, or accept the licensing to enter the market. Depending on the two scenarios for the development cost, the optimal two-part tariff licensing strategies for the innovator were investigated. It concludes that the technology is always licensed and the optimal licensing contract depends on the development cost incurred by the rival, the market parameter and the substitution coefficient.
Stackelberg duopoly;two-part tariff; product differentiation;development cost
2015-08-22
王 静(1978—),女,辽宁大连人,讲师,博士生E-mail:wjlnnu@126.com
F224; F016
A

