两大部类持续扩大再生产的优化
陶为群
(中国人民银行南京分行,南京 210004)
两大部类持续扩大再生产的优化
陶为群
(中国人民银行南京分行,南京 210004)
基于经典的马克思两大部类社会再生产公式,建立了离散确定型的持续扩大再生产的优化问题的动态规划模型.在生产资料部类的不变资本产出率高于另一部类的条件下,动态规划的指标函数是作为决策变量的生产资料部类积累率的单调函数,因而可以使用逆序解法或者顺序解法, 获得唯一的最优策略和最优指标函数.借助《资本论》中的一个举例,计算验证了最优解.
政治经济学,持续扩大再生产;优化;动态规划;逆序解法
1 引 言
马克思的两大部类社会扩大再生产理论与模型对于研究国民经济增长具有重要指导意义,两大部类持续扩大再生产的优化问题可以为国民经济持续增长的优化提供理论指导.这一优化问题本质上是一个两大部类扩大再生产的静态最优化问题序列,因此,它的解也是这一序列的静态最优化问题的序列解.两大部类持续扩大再生产优化问题的根本意义,是通过寻求序列化的最优策略(控制)而获得扩大再生产的动态最优增长路径.李海明、祝志勇(2012)把马克思扩大再生产理论与一般动态均衡分析方法结合,建立了马克思社会扩大再生产动态均衡模型,并运用最优控制方法推导模型的最优解[1].不过,他们的研究存在两个方面的不足,因而很大地削弱了获得的结果.第一, 假定了 “两大部类可变资本之比不变”.鉴于陶为群、陶川(2012)已经论证了在“两大部类可变资本之比不变” 条件下,扩大再生产的决策变量取值是被两大部类可变资本之比所唯一确定的[2],因而这个假定实际上就把扩大再生产的动态最优化问题简化成为确定状态变量的最佳初始值,改变了动态最优化问题的根本意义.第二,把两大部类扩大再生产动态模型设计成一个连续确定型模型,因而改变了经典的马克思再生产公式是离散确定型模型的基本设定.陶为群、陶川(2013) 使用“价值系数法” 简便地获得了经典的马克思两大部类扩大再生产的静态优化问题的最优解[3],并且陶为群(2015)证明了两大部类扩大再生产持续进行的充分必要条件[4].事实上,两大部类持续扩大再生产的优化问题,是一个以扩大再生产持续进行作为前提的两大部类扩大再生产的静态最优化问题序列.他们这两方面的研究结果,为求解两大部类持续扩大再生产的优化问题做了铺垫.在生产资料部类的不变资本产出率高的条件下,两大部类持续扩大再生产的优化问题可以构成一个离散确定型的动态规划,并且使用逆序解法求解(编篡委员会,2001)[5].
2 两大部类扩大再生产的当年资本积累均衡和结构状态变化

j=Ι,ΙΙ.
(1)
根据式(1)和每个部类内部,总产值的各构成部分之间保持固定不变关系,可以获得社会再生产的当年资本积累均衡方程:
(2)
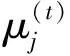
(3)
用两大部类新创造价值之间的比例
(4)
表示两大部类总产品之间的结构状态,φ(t)是社会再生产系统中的状态变量.φ(t)与资本有机构成、剩余价值率参数hj,ej共同体现了两大部类再生产系统的完整结构.由于总产值增量的各构成增量之间也保持同样的固定不变关系,将式(3)和φ(t)的表达式代入资本积累均衡方程式(2),得到:
(5)

(6)
式(6)就是扩大再生产的解.陶为群(2015)证明了[4],对于任何t年,在第Ⅰ部类资本利润率不高于第Ⅱ部类即eΙ/(1+hΙ)≤eΙΙ/(1+hΙΙ)的情形下,社会扩大再生产持续进行的充分必要条件是
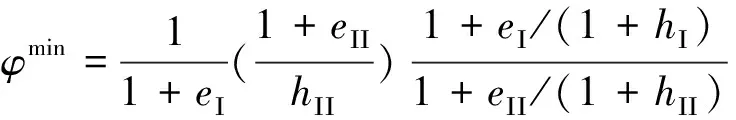
(7)
(8)
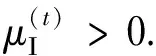
φ**≤φ(t)<φmax,式中
(9)
(10)

(11)
2个部类的新增产出总和是
(12)
能够最一般地表示社会扩大再生产的结果.因而第t+1年相对于第t年全社会的产出增长率是
(13)
将式(11)和φ(t)的表达式(4)代入式(13),得到:
(14)

(15)
资本积累使下一年社会再生产的产出增加,而2个部类的新增产出会使2大部类结构状态发生变化.下一年的两大部类结构状态与当年的状态和下一年的两个部类产出增长率有关.
(16)
当第t年实现了扩大再生产,可将式(11)代入式(16),得到:
(17)

(18)
持续扩大再生产是一序列静态意义下的社会扩大再生产的前后衔接.由于资本积累会使两大部类结构状态发生变化或者不发生变化,因而状态转移方程可以作为纽带,通过第Ⅰ部类的资本积累把前后2个相邻年份的社会扩大再生产的衔接起来.
3 两大部类持续扩大再生产的动态规划及逆序解法
全社会的产出增长能够代表经济发展.以y(t)表示第t+1年相对于第t年的经济发展速度.则
(19)
将式(15)代入式(19),得到经济发展速度与决策变量之间的关系式:
(20)
第t+1年的产出与当年的经济发展速度和第t年的产出具有确定的关系:
Y(t+1)=Y(t)y(t)
(21)
考察持续n+1年的扩大再生产,对于k=1,2,…,n,根据式(21),第k+1年的全社会产出是被第1年的产出和此后各年的全社会经济发展速度所确定.
(22)
根据式(20),决策变量影响着发展速度,因而经济发展速度可以作为指标函数.
当考察持续n+1年的社会扩大再生产,根据式(22)需要确定n个年份对于前一年的发展速度, 因而阶段变量是n.扩大再生产的状态变量从第k年的φ(k)到第k+1年的φ(k+1)之间,对应的阶段指标是第k+1年相对于第k年的经济发展速度y(k)(k=1,2,…,n).当从第k年的两大部类的结构状态φ(k)出发,采用后部k段子策略,则后部指标函数是:
(23)
由于指标函数是阶段指标的乘积,因而可以分离,根据式(23),有:
k=1,2,…,n-1.
(24)
在一定条件下,式(18)、(20)和(24)可以构成一个持续n+1年的社会扩大再生产的动态规划,并且可以使用逆序解法求解.
根据式(23)可以确定,在从第k年的状态φ(k)到第n+1年的终止状态的后部子过程,最优指标函数是
(25)
使用逆序解法,根据式(24)和(25)可以列出持续n+1年的社会扩大再生产的逆序动态规划方程:
k=n,n-1,…,2,1
(26)
式(26)当中的第二式为边界条件.式(20)和(26)构成动态规划的逆序解法的基本方程.
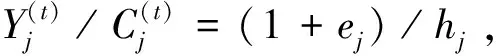
(27)


).根据式(8)和式(10),可以明确地写出qΙ(φ(t)).在第Ⅰ部类资本利润率不高于第Ⅱ部类即eΙ/(1+hΙ)≤eΙΙ/(1+hΙΙ)的情形下,
t=1,2,…,n.
(28)
在第Ⅰ部类利润率高于第Ⅱ部类即eΙ/(1+hΙ)>eΙΙ/(1+hΙΙ)的情形下,
t=1,2,…,n.
(29)
于是在第n年的最优决策是:
(30)
×Max(y(n-1)).
(31)

4 两大部类扩大再生产的动态规划最优策略和整体最优函数
根据后部子过程的最优指标函数式(25)和逆序动态规划方程式(26),原过程的整体最优函数是:
(32)
由于初始年状态变量φ(1)是既定的,因而根据以上解析结果以及式(28)或者式(29),可以确定:
(33)
进而根据状态转移方程式(18)和式(28)或者式(29),可以顺序逐年迭代确定:
t=1,2,…,n-1 .
(34)
将式(33)和(34)代入整体最优函数f1(φ(1)),f1(φ(1))就得以最终确定.
(35)
根据式(33)和(34),也最终确定从第1年到第n+1年原过程的最优策略.
(36)
式(36)清晰地表明:持续n+1年扩大再生产的动态优化问题的最优解,是一序列的静态最优化问题的序列解.扩大再生产的初始状态φ(1)和原过程的最优策略共同确定了持续扩大再生产的最优增长路径.
从以上解析的过程看到,持续n+1年的社会扩大再生产优化的动态规划也可以使用顺序解法求解.
综合以上解析的结果,在第Ⅰ部类的不变资本产出率高于第Ⅱ部类的条件下,只要初始年状态变量φ(1)满足扩大再生产的充分必要条件式(7)或者式(9),那么式(20)、(25)、(26)可以构成一个持续扩大再生产优化的动态规划,并且可以使用逆序解法或者顺序解法求解.全部过程的最优策略由式(33)、(34)和(36)表示;整体最优函数的取值由式(33)、(34)和(35)共同表示.最优策略和整体最优函数的取值都是被两个部类的资本有机构成、剩余价值率参数和初始年结构状态φ(1)唯一确定.
考虑连续n+1年的扩大再生产优化,应当以在n+1年里相对于初始产出Y(1)的各年新增产出总和最大作为目标函数;也就是以n+1年里的各年产出总和最大作为目标函数.根据式(22),n+1年里各年产出总和是
(37)
在第Ⅰ部类的不变资本产出率高于第Ⅱ部类的条件下,只要初始年状态变量φ(1)满足扩大再生产的充分必要条件式(7)或者式(9),则第k+1年的最大产出是
k=1,2,…,n.
(38)
各年产出的总和最大值是
(39)

5 数值计算两大部类持续扩大再生产的最优解
下面借助马克思《资本论》第二卷第二十一章中的第二例[6],对以上获得的持续扩大再生产的动态规划的最优解,进行数值计算验证.此例设定两个部类结构参数hⅠ=5,hⅡ=5.017 5,eⅠ=eⅡ=1,满足第Ⅰ部类的不变资本产出率高于第Ⅱ部类的条件.马克思用此例做了连续三年的计算,说明一般情形下两个部类的扩大再生产过程.该例是本文所论析的第Ⅰ部类的资本利润率高于第Ⅱ部类即eΙ/(1+hΙ)>eΙΙ/(1+hΙΙ)的情形.直接引用该例中的第1年(起始年)数据,列在表1中的第1年的前3列.根据式(9),计算出φ**=0.199 8,φmax=0.398 6;于是两大部类社会再生产的结构状态变量取值区间是半开区间[0.199 8, 0.398 6 ).第1年两大部类社会再生产的结构状态变量φ(1)=0.285, 处于上述半开区间内,满足两大部类扩大再生产持续进行的充分必要条件式(9).


表1 举例验算两大部类持续扩大再生产的最优解
6 结 论
综合以上研究结果表明,基于经典的马克思两大部类社会再生产公式,可以建立离散确定型的持续扩大再生产的优化问题的动态规划模型,并且在生产资料部类的不变资本产出率高的条件下,使用逆序解法或者顺序解法获得唯一的最优解.最优解是被两个部类的资本有机构成、剩余价值率参数和初始年结构状态所确定.
[1] 李海明,祝志勇.扩大再生产的动态最优模型[J],经济科学,2012(6):12-22.
[2] 陶为群、陶川.马克思经济增长模型中的特征值及其理论蕴涵[J].经济评论,2011(3):5-11.
[3] 陶为群,陶川.两大部类扩大再生产中的广义拉格朗日乘子[J].经济数学,2013,30(4):49-54.
[4] 陶为群. 两大部类扩大再生产的按比例发展定理 [J].经济数学,2015,32(2):60-65.
[5] 编篡委员会.现代数学手册经济数学卷[M].武汉:华中科技大学出版社,2001:351-363.
[6] 马克思.资本论(第二卷) [M].北京:人民出版社,2004:579-585.
The Optimization of the Two-sector Continuous Expanded Reproduction
TAO Wei-qun
(Nanjing Branch, The People’s Bank of China, Nanjing, Jiangsu 210004, China)
Based on classical Marx's two-sector reproduction scheme, this paper established a dynamic programming model of the optimization problem of the continuous expanded reproduction. The model is a dispersed and determined type. Depending on the condition that the constant capital output ratio of the capital goods sector is higher than that of another sector , the target function in the dynamic programming is a monotone function of the accumulation rate of the capital goods sector , which is treated as a decision variable. Therefore, only the optimum strategy and optimum target function can be obtained by the inverted sequence solution. An example from Marx's "Das kapital" was drawn upon to verify the optimum solution.
political economy; continuous expanded reproduction; optimization; dynamic programming; inverted sequence solution
2015-06-07
陶为群(1955—),男,江苏南京人,研究员,硕士 E-mail:taoweiqun@aliyun.com
F224,F014.3
A
——基于三大部类再生产图式的结构分析*

