框支密肋复合墙结构振动台试验与数值模拟分析
何玉阳,袁 泉
(北京交通大学 土木建筑工程学院,北京 100044)
框支密肋复合墙结构是由底部框架和上部密肋复合墙组成的一种新型结构体系。黄炜等[1-2]通过对密肋复合墙结构的试验研究及理论分析表明:密肋复合墙结构中的填充砌块、密肋框格及隐形框架整体工作性能较好,在地震作用下能够逐渐发生损伤破坏并耗散地震能量,从而改变结构的振动特性,提高结构的抗震性能。
历次震害分析表明,建筑结构失效倒塌是引起大量人员伤亡和经济损失的根本原因。模拟地震振动台试验在结构抗震性能研究中具有重要的意义,试验可以较真实的模拟结构在地震作用下的破坏过程、破坏机理、薄弱环节等,进而对结构设计提出改进建议,同时模拟地震振动台试验也是验证数值模拟有效性、可行性的重要手段,因此国内外学者进行了大量的各种结构的模拟地震振动台试验[3-8]。
本文在框支密肋复合墙结构的整体抗震性能振动台试验的基础上,以ABAQUS软件为计算平台,建立非线性有限元模型,对结构在试验的几种典型工况下的地震反应进行数值模拟计算,并将试验结果与数值模拟计算结果进行对比分析。
1 振动台模型试验简介
1.1 模型设计
模型的相似关系按原型的1/6选取二托三结构,共5层平面尺寸为1.78 m×1.10 m,其他层框架柱侧面长120mm,第一层层高0.6 m、第二层层高0.7 m,其它层层高均为0.5 m。固定在振动台上的模型如图1。

图1 模型加载图Fig.1 Load of model
1.2 试验加载方案
根据实际模型所处场地条件和研究需要,本实验选取比较典型的Taft波,El-Centro波,人工波进行振动台试验。其中,人工波根据规范反应谱和场地条件要求自行生成。
考虑模型相似关系,考虑地震波主要频带不超出振动台可再现范围(0.1~50 Hz),而且输入点在4096个以下,对原始波分段采样和按周期(时间)相似比0.29进行频率压缩,幅值根据加速度幅值相似比2.5调幅,调整和压缩的各地震波波形如图2(a),(b),(c),(d)。
在每级加载前都进行白噪声激励,以获得相应的频率和振型。试验时测试各级荷载下的自振频率,并记录了模型各层的加速度和层间位移,整个测试过程所有工况见表1。

表1 加载工况Tab.1 Loading mode
2 有限元模型的建立
本文运用有限元软件ABAQUS建立非线性有限元模型。模型中墙体采用实体单元C3D8R,钢筋采用桁架单元T3D3。使用Embedded Element功能将钢筋骨架嵌入剪力墙,整体结构有限元模型见图3,钢筋有限元模型见图4。
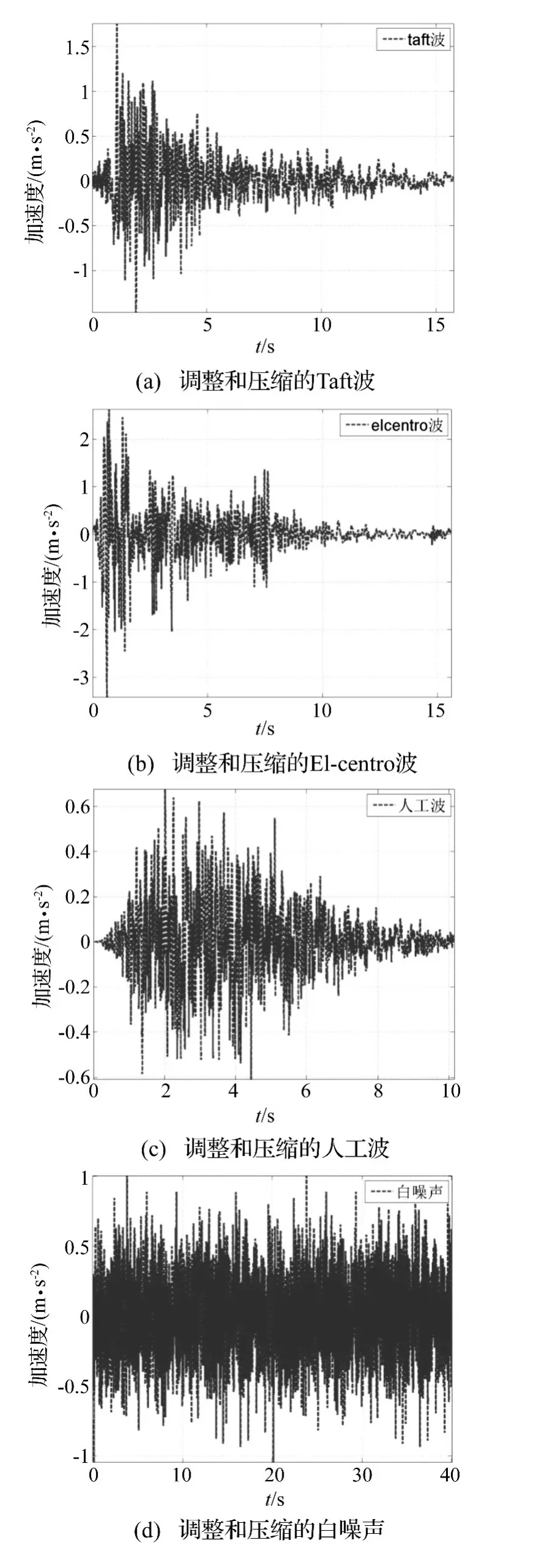
图2 调整和压缩的各地震波波形Fig.2 Adjust and compression seismic waveform
3 试验结果与数值模拟对比分析
3.1 各工况下的加速度对比分析
表2给出了在不同工况下,试验和有限元模拟的结构各层加速度数值的对比情况。从表中的数据来看,第一层、第二层、第三层的加速度响应比第四、第五层小,顶层加速度最大,第三层加速度突增,特别是在1.2 g工况下,相比工况1.0 g,第三层、第四层、第五层加速度成非线性突增,说明框支密肋复合墙结构第三层已经出现较大程度的破坏。此现象表明,第三层为较为薄弱,刚度相对第二层有突变,随着地震动强度的增加,第三层的加速度增加速率最快,有可能发生脆性破坏。

图3 整体结构有限元模型Fig.3 The overall structure finite element model

图4 钢筋有限元模型Fig.4 Reinforced the finite element model
有关各工况下结构各层加速度的具体图示,本文选取了使结构出现裂缝的0.65 g地震波和使结构达到最大破坏的1.2 g地震波,分别如图5和图6所示。由表2以及图5和图6得出,试验数据和有限元模拟有很好的对比。

表2 不同工况下结构各层的加速度Tab.2 Under the different conditions of each layer of the structure acceleration
3.2 各工况下的层间位移角对比分析

图5 0.65 g作用下加速度对比图Fig.5 Acceleration contrast figure under the condition of0.65 g
图7 展示了 EL-Centro波在工况 0.65 g~1.2 g下试验采集的和有限元模拟的层间位移角对比图,由对比可知:试验采集的和有限元模拟的层间位移角的大小分布规律一样,第一层、第二层、第三层的层间位移角比四、五层的大,最大值出现在第二层和第三层,表明第二层、三层为整个结构的薄弱层。
按照《建筑抗震设计规范》要求,弹性层间位移角限值取1/800,弹塑性层间位移角限值取1/100。本文按相似比1/6将其缩放后,分别为2.1×10-4和16.7×10-4,以此对各工况的数据进行分析,发现,第一层、第二层、第三层、第四层、第五层均超过规范的弹性限值,同时又远远小于规范的弹塑性限值,说明整个结构均已进入塑性状态,结构的第二层、第三层出现突增的现象,说明结构在第二层、第三层出现了严重的破坏,产生了较大的塑性变形,消耗了大部分的能量,导致第四、五层的地震响应降低。随着地震加速度的增大,各层的层间位移角逐渐增大,整个结构虽渐渐达到极限承载能力状态,但仍满足大震不倒的抗震要求。试验数据和有限元数据有很好的对比。
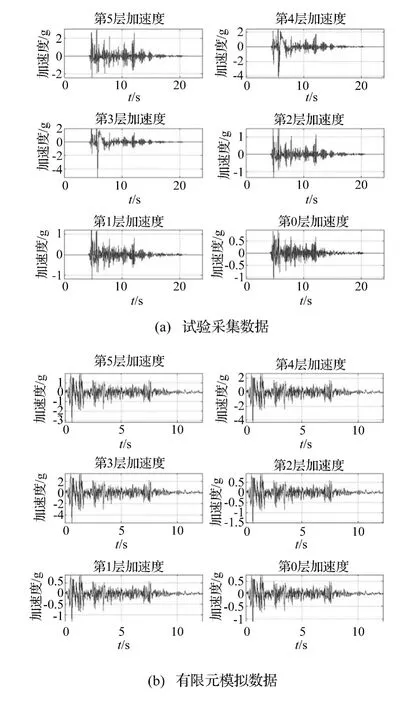
图6 1.2 g作用下加速度对比图Fig.6 Acceleration contrast figure under the condition of1.2 g
3.3 各工况下的破坏形态对比分析
在工况0.65g下:从试验现象来看,第一层剪力墙开始出现水平裂缝和斜裂缝;第二层的上部柱角开始出现斜裂缝;第三层密肋复合墙底部出现一条水平裂缝;在有限元模拟的图9中亦呈现出类似破坏样式。
在工况0.75 g下:从试验现象来看,第一层剪力墙的水平裂缝和斜裂缝,其宽度和长度均有所发展,墙体底部渐渐形成一条贯穿性的水平裂缝;第二层的上部柱角水平裂缝进一步延伸,连梁上部开始出现斜裂缝;第三层密肋复合墙底部水平裂缝长度进一步延伸,肋格与填充砌块的接触部分开始出现大量水平裂缝和垂直裂缝;在有限元模拟的图10中,可明显发现第一层剪力墙处裂缝开展方式以及第三层密肋复合墙底部的水平裂缝与试验破坏图极为相似,试验的结构破坏形态和有限模拟的结构破坏形态有很好的对比。

图7 各工况地震波作用下结构层间位移角对比图Fig.7 The effect of each working condition under seismic wave structure layer displacement angle comparison chart
在工况0.85 g下:从试验现象来看,第一层剪力墙的水平裂缝和斜裂缝扩大延伸更加明显,相继出现了许多新的水平裂缝;第二层的框架柱的中上部出现了新的斜裂缝,同时剪力墙原有的垂直裂缝及斜裂缝进一步扩大延伸,第二层连梁的垂直裂缝及斜裂缝进一步扩大;第三层密肋墙板中裂缝在原有基础上不断扩展和增加,第四层的密肋复合墙板也出现了不同程度的斜裂缝和水平裂缝。上述现象在其有限元模拟图11中也得到了很好的体现。
在工况1.0 g下:从试验现象来看,第一层的剪力墙和框架柱,其水平裂缝和斜裂缝均在原有基础上继续扩大延伸,且不断有新的裂缝出现;第二层的框架柱的斜裂缝继续扩大延伸,剪力墙的斜裂缝和垂直裂缝继续扩大延伸;第三层密肋复合墙中肋格与填充砌块间的水平裂缝和垂直裂缝大部分已相互贯通;第四层密肋复合墙中肋格与砌块间的裂缝也相继增多,但墙板底部的水平裂缝发展不明显。上述现象在其有限元模拟图12中亦得到了很好的体现。
在工况1.2 g下:从试验现象来看,第一层剪力墙的水平裂缝和斜裂缝相互贯通,并出现一条主斜裂缝贯穿整片墙体,第一层的框架柱的水平裂缝贯穿整根柱;第二层的框架柱的斜裂缝继续扩大延伸,剪力墙的斜裂缝和垂直裂缝扩大延伸并已贯通成一条主裂缝;第三层密肋复合墙底部的水平裂缝已经贯通,墙板中肋格与砌块都呈现了一定程度的破坏,这一点完全符合密肋复合墙结构墙板、肋格、砌块三道防线的破坏机理;第四层密肋墙底部的水平裂缝发展较明显。从有限元模拟的结果来看,第一层、第二层、第三层损伤破坏最为明显,第四层、第五层次之,这说明本结构的薄弱层为第一层、第二层、第三层,破坏形式以剪切破坏为主。试验的结构破坏形态和有限模拟的结构破坏形态图13有很好的对比。

图8 试验情况下结构各层破坏形态Fig.8 The test case structure of each layer damage morphology

图9 0.65 g作用下有限元模拟破坏形态Fig.9 Finite element simulation of failure modes under the condition of 0.65 g

图10 0.75 g作用下有限元模拟破坏形态Fig.10 Finite element simulation of failure modes under the condition of0.75 g

图11 0.85 g作用下有限元模拟破坏形态Fig.11 Finite element simulation of failure modes under the condition of0.85 g

图12 1.0 g作用下有限元模拟破坏形态Fig.12 Finite element simulation of failure modes under the condition of1.0 g
4 结论
本文根据框支密肋复合墙结构的实际模型按照相似比1/6缩放后构建有限元模型,并对其按工况0.65 g、0.75 g、0.85 g、1.0 g、1.2 g 进行非线性有限元时程分析,通过对试验结果与有限元分析结果进行对比分析,得出:

图13 1.2 g作用下有限元模拟破坏形态Fig.13 Finite element simulation of failure modes under thecondition of1.2 g
(1)本文运用有限元软件ABAQUS建立非线性有限元模型。模型中的混凝土墙体和柱均采用实体单元C3D8R,混凝土采用损伤模型,钢筋采用桁架单元T3D3,通过有限元数据和实验数据对比,这种混凝土损伤模型不但降低了数值分析的难度和耗时,而且能够很好的模拟框支密肋复合墙结构的破坏形态和过程,可以为今后该结构的工程应用提供更好的设计基础。
(2)在对模型结构进行模拟过程中,其破坏时对应的地震加速度峰值为1.0 g,因此,其对应的原型结构的破坏地震加速度为1.0 g/2.5=0.4 g,说明结构可以承受八度设防地区大震的冲击,同时由结构各层层间位移角远远小于规范中的弹塑性限值,可知结构可以满足规范大震不倒的要求。
(3)由有限元模拟混凝土的损伤程度得出,第一层、第二层、第三层的损伤面积和程度较大,由层间位移角得出最大的层间位移角出现在第二层、第三层,并且第一层的剪力最大,已发生剪切破坏。第三层密肋复合墙的破坏模式完全符合其墙板、肋格、砌块三道防线的抗震机理。
[1]黄炜,陈国新,姚谦峰,等.基于统一强度理论的密肋复合墙体开裂荷载计算[J].工程力学,2008,25(7):94 -99.HUANG Wei,CHEN Guo-xin,YAO Qian-feng,et al.Calculation on cracking load of multi-ribbed composite wall based on twin shear unified strength theory[J].Engineering Mechanics,2008,25(7):94 -99.
[2]郭猛,姚谦峰.框架-密肋复合墙结构新体系研究[J].地震工程与工程振动,2009,29(5):73 -78.GUO Meng,YAO Qian-feng.Research on frame-multi-ribbed composite wall structure new system [J]. Earthquake Engineering and Engineering Vibration,2009,29(5):73-78.
[3]Martinelli P,Filippou F C.Simulation of the shaking table test of a seven-story shear wall building [J]. Earthquake Engineering and Structural Dynamics,2009,38(5):587-607.
[4]Chung Y L,Takuya N,Toko H,et al.Seismic resistance capacity of high-rise buildings subjected to long-period ground motions:E-defense shaking table test[J].Journalof Structural Engineering,2010,136(6):637 -644.
[5]李荣华,邸庆霜,杨树标,等.钢筋混凝土框架振动台试验模型的数值模拟研究[J].河北工程大学学报:自然科学版,2009,26(2):22 -25.LI Rong-hua, DI Qing-shuang, YANG Shu-biao, et al.Numerical simulation of a RC frame shaking table test model[J].Journal of Hebei University of Engineering:Natural Science Edition,2009,26(2):22 -25.
[6]赵亚敏,苏经宇,周锡元,等.碟形弹簧竖向隔震结构振动台试验及数值模拟研究[J].建筑结构学报,2008,29(6):99-106.ZHAO Ya-min,SU Jing-yu,ZHOU Xi-yuan,et al.Shaking table test and numerical analysis of vertical isolated building model with combined disk spring bearing[J].Journal of Building Structures,2008,29(6):99 -106.
[7]赵亚敏.三维基础隔震结构体系理论与振动台试验研究[D].北京:北京工业大学,2007.
[8]朱杰江,吕西林,邹昀.上海环球金融中心模型结构振动台试验与理论分析的对比研究[J].土木工程学报,2005,38(10):18-26.ZHU Jie-jiang,LÜ Xi-lin,ZOU Yun.Shake-table test and theoretical analysis for Shanghai World Financial Center scale model[J].China Civil Engineering Journal,2005,38(10):18-26.
[9]袁泉,何玉阳.框支密肋复合墙结构模型振动台试验研究[J].振动与冲击,2014,33(22):72 -77.YUAN Quan,HE Yu-yang.Earthquake simulation test on multi-ribbed composite wall supported on frame[J].Journal of Vibration and Shock,2014,33(22):72 -77.

