基于时域谱单元的功能梯度材料结构波传播分析

徐 超，王 腾

(西北工业大学 航天学院，西安 710072)

功能梯度材料的宏观材料特性表现出空间连续变化的性质。材料成分和性质的变化会改变弹性波在结构中的传播行为，研究弹性波在功能梯度等非均匀材料结构中的传播特性对发展新材料结构的损伤检测和健康监测方法具有重要的意义［1］。

与传统均质材料不同，功能梯度材料的弹性模量、泊松比等宏观性质都随空间位置而变化，采用解析解或半解析方法研究功能梯度材料结构中的波传播行为十分困难。文献［2］基于Hamilton变分原理和高阶剪切变形理论推导了在点冲击下无限大功能梯度材料板应力波的近似解析解。文献［3］采用一阶剪切变形理论和小应变的应变－位移关系，研究了四边固支板中，不同功能梯度材料指数对波传播行为的影响。文献［4］采用连续材料模型，利用Legendre多项式展开方法获得了功能梯度材料板的频散和功率流解。文献［5］应用幂级数展开方法研究了Lamb波在功能梯度材料板结构中的传播行为。然而，这些工作多局限于一维梯度材料，并且研究对象均为边界条件和几何较为简单的结构。

谱单元法是求解复杂结构弹性波传播行为的一种新型数值方法。文献［6］最早在计算流体问题研究中提出了谱单元法，其充分结合了谱方法的快速收敛和有限元法对复杂结构适应性好的优点，特别适合求解瞬变和高频动力学问题。文献［7］将谱单元推广用于弹性波传播的模拟，并求解了一维均匀材料杆结构中的波传播问题。文献［8－10］则进一步地将谱单元法用于二维和三维结构波传播问题。由于功能梯度材料性质在结构中的空间变化特性，应用谱单元法求解功能梯度材料的结构波传播问题的研究还不多。文献［11－12］采用频域谱单元建立了新的功能梯度材料梁单元，用于冲击载荷下功能梯度梁的波传播问题。文献［12］建立了一种基于切比雪夫多项式时域谱单元，并将其用于求解平面功能梯度材料结构中的波传播问题。

本文推导了一种具有任意四边形形状的Gauss－Lobatto－Legendre多项式时域谱单元用于功能梯度材料结构中弹性波传播行为的模拟。分别采用连续材料模型、分层离散模型和均匀化模型建模功能梯度材料宏观性质空间变化特性。将数值计算结果与理论解进行了对比以验证单元有效性，研究了面内受水平激励的功能梯度材料板结构的波传播特性，对比了三种材料建模方法的差异。

1 任意四边形谱单元推导

1.1 位移、形状插值

如图1所示，与传统有限元不同，自然坐标系下标准谱单元的节点非等距地分布于区域Λ∈［－1，1］2内，单元上节点坐标位置根据特殊多项式的零点确定。非等距节点布置能有效克服等距节点布置在插值时引起的龙格效应。这里采用 Gauss－Lobatto－Legendre多项式确定单元中各节点的坐标位置。以ξ方向为例，Gauss－Lobatto－Legendre 多项式为

式中:Pn－1(ξ)为n－1阶勒让德多项式。单元阶次不同，对应的节点坐标位置不同，如当n=5时，节点ξ方向坐标为

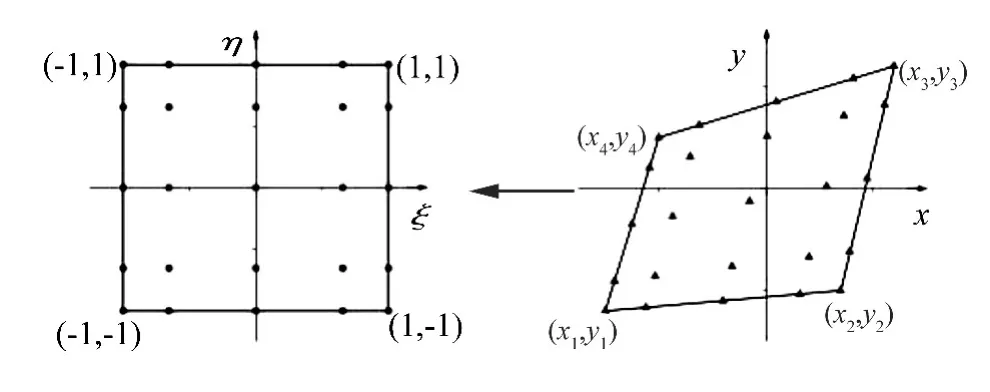
图1 2D谱单元及5×5节点分布Fig.1 2D spectral element with 5 ×5 nodes

同理，单元η方向上的节点坐标也可类似确定。

仍采用拉格朗日插值函数对单元内位移场进行插值，即

式中:u，v分别为 x，y方向的位移。ψm(ξ，η)=φi(ξ)φj(η)，m=1，2，...，n2，φ 为单变量拉格朗日插值函数。

实际应用中，剖分离散后的单元几何形状可能不是标准的边长为1的正方形。考虑单元形状为任意四边形的情况，需进行形状插值建立任意四边形单元与标准谱单元的几何映射关系。

设任意四边形四个角节点的坐标为(xk，yk)，k=1，2，3，4，采用一阶拉格朗日插值函数建立单元形状插值关系:

1.2 功能梯度材料模型

考虑材料性质一维变化的功能梯度材料，其弹性模量E、泊松比ν和密度ρ都沿某一方向规律变化。对于二维情况，不失一般性，假设材料性质沿y方向变化。由于功能梯度材料的特点，进行数值计算时需要采用特殊的材料模型。常用材料建模方法有三种:

(1)均匀化模型:忽略掉材料性质的梯度变化，采用材料性能的平均值作为均匀化的材料属性。

(2)分层离散模型:将功能梯度材料沿材料性质变化方向离散为若干材料层，材料层内各单元材料性质都为同一常数。原则上讲，分层模型解会随着分层数增加趋于解析解，相应的计算效率也会下降。

(3)连续材料模型:将材料属性考虑为坐标的连续函数，则单元内材料性质也是坐标的连续函数，材料密度矩阵μe和弹性矩阵De可表示为:

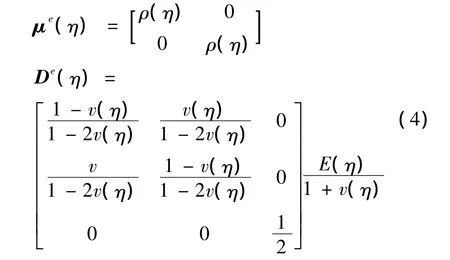
一般地，采用体积分数函数g(y)来描述材料属性的变化。这里设f(y)为空间某一材料属性值，在单元内部，则由式(3)可知有f(y(η))。假设fu，fd分别为结构上下表面的材料属性值，则有

g(y)一般为幂函数形式，即

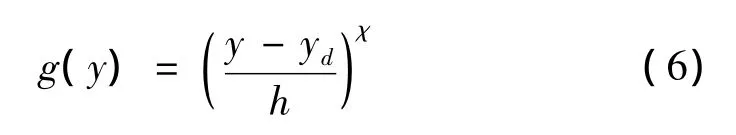
式中:yu，yd代表结构上下界面的坐标，h=yu－yd。χ表示材料分布的不同梯度，当χ=0为均匀材料。

本文将分别采用上述材料建模方法研究功能梯度材料结构中的波传播特性，对比不同的材料模型对结构中波传播行为的影响。

1.3 单元刚度和质量矩阵

利用上述位移和形状插值函数，根据Hamilton原理建立变分方程，可推导获得单元质量矩阵Me，单元刚度矩阵Ke和单元上的等效外力Fe表达式为:

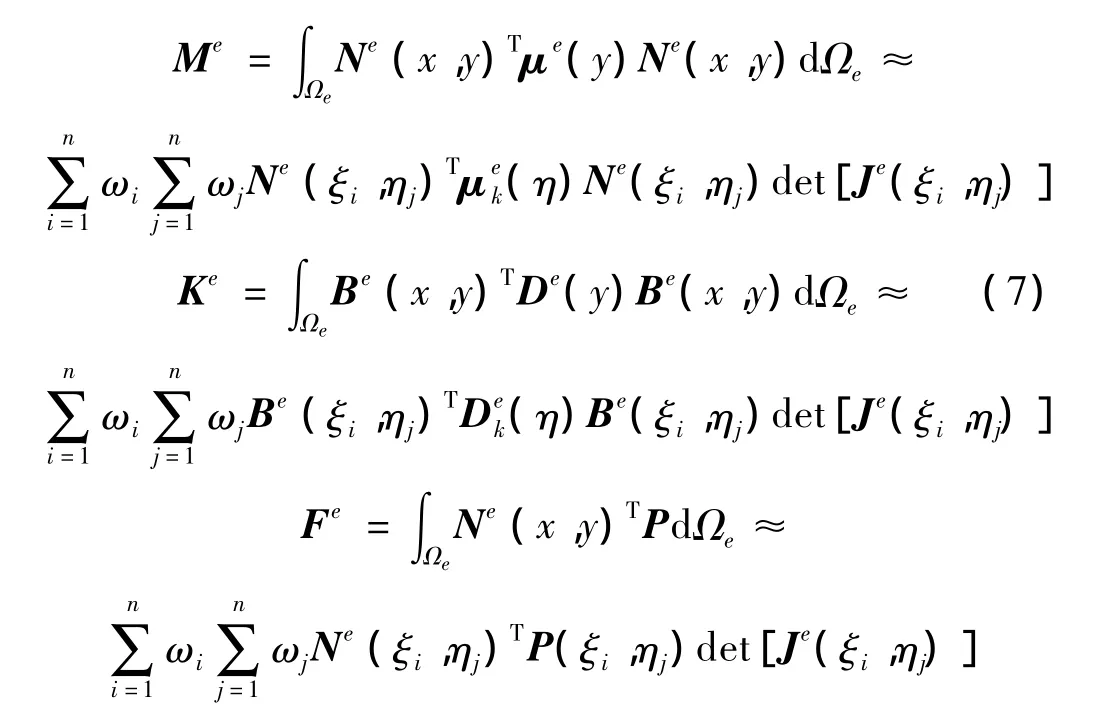
式中:Be矩阵为几何矩阵，可以由位移－应变几何关系求出:

式(7)中 μe(η)，De(η)如为连续材料模型时采用式(4)－(6)的，其值由积分点位置确定;如为材料模型Ⅰ和Ⅱ时，取为相应均匀化后的常数值。

式(7)中J为雅克比矩阵，描述任意四边形单元与标准谱单元的几何关系，根据式(3)有

对式(7)采用 Gauss－Lobatto－Legendre(GLL)数值积分求解，积分系数ωi＞0，可由下式确定:

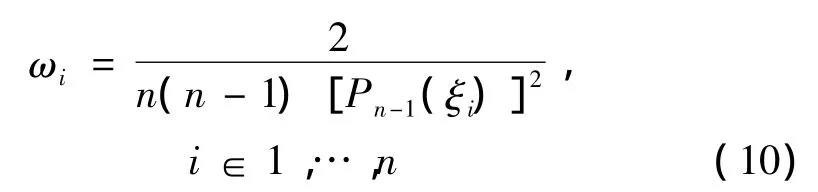
由于勒让德多项式的正交性，单元质量矩阵为对角矩阵，这可显著降低波动力响应时域求解的计算耗费，较切比雪夫多项式时域谱单元有明显优势。

2 数值算例

2.1 中心受垂直冲击载荷的无限大FGM板

为了验证所推导单元的有效性，考虑一中心受载的无限大FGM板。文献［2］采用弹性板壳理论，考虑高阶剪切变形与转动惯量的影响，推导获得了极坐标下的解析解。本文采用平面应变模型，利用前文推导的连续材料模型谱单元离散板结构，将获得的数值解与解析解进行对比。

如图2所示，板厚度为0.02 m，材料属性沿厚度方向线性变化，即χ=1。板上、下界面材料属性分别为铝和氧化锆，弹性模量分别为70GPa、151GPa，密度分别为 2700 kg/m3、3000 kg/m3，泊松比为常值 0.3。冲击激励形式为5个周期经过调制的正弦信号。

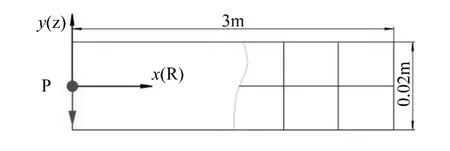
图2 板的二维模型Fig.2 Two－dimensional model of plate

应用谱单元数值求解时，单元尺寸为0.01×0.067 m，每个单元节点数为5×5，积分步长取2×10－8s，监测距加载处x=2 m处的响应和解析解对比。采用文献［2］中的无量纲方法，无量纲后的时域响应如图3(a)、(b)所示。其中，图3(a)给出了x方向的位移响应，图3(b)给出了y方向的位移响应。由图可知，数值解和解析解吻合较好，验证了本文推导单元的有效性。需要说明的是，这里是依据平面应变假设进行数值求解，给出了近似解，目的是验证单元的波传播描述能力。由于连续材料模型的单元精度也受单元规模和积分阶次制约，给出的解也是数值近似解，因此图3种仍存在小量误差。

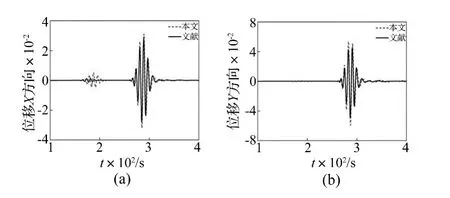
图3 在x=2 m处，板上表面X方向的位移和中面Y方向的位移Fig.3 The displacements x on top surface and deflection y on middle plane of plate at x=2 m

2.2 面内一端受水平激励的FGM板

2.2.1 模型描述

如图4所示，一个陶瓷－铬混合功能梯度板在xy面内的截面，其材料属性见表1。板厚20mm，长2 m，在左端施加水平的均匀分布载荷，激励信号为中心频率为50 kHz经汉宁窗调制的正弦信号，时长三个周期，信号峰值109N/m，见图5。采用7×7节点谱单元计算，单元尺寸为0.005×0.05 m。动力学方程采用中心差法求解，积分步长为2×10－2μs。

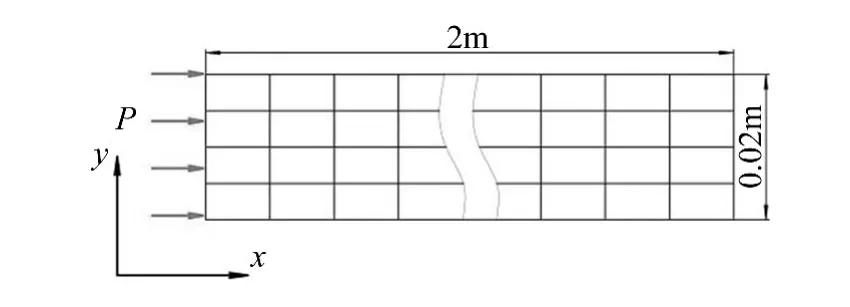
图4 板xy截面及计算网格Fig.4 Plane xy of plate and computational grids

图5 中心频率为50 kHz的激励波形Fig.5 The excitation with the center frequency 50 kHz

公开文献中对于FGM板时域求解的方法仍主要集中于分层取均值等分层离散方法［14］，本文采取三种材料模型进行对比求解。三种材料模型采用同一网格，同一单元阶次，同一积分方法，只是单元材料属性模型不同，从而通过波场、时域响应，相速度频散对比，研究其对功能梯度材料结构波传播行为的描述能力差异。

表1 FGM材料属性Tab.1 Functional Graded Materials properties

2.2.2 波场及时域响应

左端施加激励后，导波会沿着板截面传播，同时受到上下边界的约束。

图6给出了采用三种不同的材料模型计算出的结构在200μs时x、y方向的位移场云图。在二维结构中，由于泊松效应，水平方向的激励在水平和垂直方向都引起结构的振动。在水平方向，能量主要集中在以对称模式S0波传播的模态上;在垂直方向，能量主要集中以反对称模式A0波传播的模态上。

由图6可以看出，在水平和垂直方向，采用三种材料模型计算得到波场云图并不相同。在x方向，200μs时，采用连续材料模型计算得到的波前位置最靠后，表明计算的波速较采用均匀模型和分散离散模型低。特别注意的是，采用均匀化材料模型只能计算得到对称模式的波包，无法计算出紧随其后的反对称模式波包。在y方向，也有类似的结果。

为了进一步定量研究不同模型对波动响应的影响，取板上表面的中点作为数值结果时域响应的提取点(因一般压电传感器贴在结构上表面，监测局部响应)，给出其0～400μs的位移响应，结果如图7所示。

图7(a)、(b)分别给出了监测点x、y方向0～400 μs的位移响应。由图可知，分层离散模型和连续模型得到的纵波和横波均含有两个波包，即对称和反对称模态的波，其中纵波幅值大于横波，先出现的波包大于后出现的;而采用均匀化模型只能计算出一个波包。采用均匀化材料模型与采用分层离散模型计算得到的波幅值和相位较为一致，而与采用连续材料模型计算的波形结果差别较大。

采用不同计算模型而导致波场、时域响应产生差异的主要原因在于，功能梯度结构的宏观材料属性沿板厚度方向线性变化，结构中相当于存在很多材料界面，使得结构中同时出现对称和反对称模态的波。均匀化模型假设材料属性不变，因此只能得到单一模态的波;分层离散模型，采用分层均匀化的方法建模材料属性的空间变化特性，模拟精度取决于结构离散程度;连续模型在单元内、外部同时考虑材料属性的连续变化，能够准确复现功能梯度材料结构中的波传播行为。

图6 不同材料模型下t=200μs时结构的位移场，单位μm。Fig.6 Displacements(unit:μm)field with the three models of material properties at 200μs

图7 不同模型计算下监测点x，y方向的位移响应Fig.7 Displacements of the receiver under the different models in x and y direction

2.2.3 相速度的频散

高频导波在板中传播会发生频散现象，即波速、频率会随着传播距离发生变化。进一步地，利用板上表面各个响应提取点(均布的41个点)的前400μs x、y方向的时域响应，去除边界反射波的影响，采用Zero－Crossing方法［15－16］，可以计算出相速度在传播过程中随频率的变化，研究不同材料模型对导波相速度频散的影响。

图8(a)、(b)分别给出了采用三种不同模型求解得到的x方向位移响应S0模式下、y方向位移响应A0模式下的相速度。可以看到，每一种模型求解得到的相速度在一定频域内，大小基本保持不变，没有出现明显的频散现象。模型Ⅰ、Ⅱ相速度比较接近;而模型Ⅲ与模型Ⅰ、Ⅱ相比，差异较大。

从以上相速度结果可以发现，首先出现的A0、S0模式下波的相速度频散现象不明显;不同模型间的相速度数值差异，说明采用均匀化假设和有限程度的分层离散求解功能梯度材料结构波传播的相速度的误差较大。

图9中给出了采用模型Ⅱ、Ⅲ求解得到的y方向S0模式波的相速度。可以看到，一定频率范围内，每一种模型求解得到的相速度大小随频率增大而增大，出现明显的频散现象。采用分层离散模型计算得到的相速度高于采用连续材料模型计算得到的值。

图8 三种模型求解得到x方向S0模式、y方向A0模式的相速度Fig.8 Phase velocity of mode S0 in x direction and mode A0 in y direction solved by the three models

图9 模型Ⅱ、Ⅲ求解得到y方向A0模式的相速度Fig.9 Phase velocity of mode A0 solved by the modelⅡ、Ⅲ in the y direction

3 结论

本文推导了一种任意四边形形状的二维Gauss－Lobatto－Legendre时域谱单元，采用连续材料模型在单元内部考虑材料属性的连续变化，并将其用于超声导波在功能梯度板结构中的波传播分析。分别比较了均匀化模型、分层离散、连续材料模型对结构波场、时域响应、相速度频散行为的影响。主要结论如下:

(1)与理论解比较，验证了推导单元的有效性。

(2)三种模型比较，均匀化模型无法准确描述功能梯度材料结构中的波场行为;采用分层离散模型计算的波响应幅值、相位和相速度均与采用连续材料模型计算的结果有差异。采用连续材料模型能更好模拟功能材料宏观材料性质空间连续变化的特征。

(3)功能梯度材料中对称模式纵波、反对称模式横波的相速度频散现象不明显，对称模式横波的相速度频散明显。

［1］仲政，吴林志，陈伟球.功能梯度材料与结构的若干力学问题研究进展［J］.力学进展，2010，40(5):528－541.ZHONG Zheng，WU Lin－zhi，CHENG Wei－qiu.Progress in the study on mechanics problems of functionally graded materials and structures［J］.Adv Mech，2010，40(5):528－541.

［2］Sun D，Luo S N.Wave propagation and transient response of a FGM plate under a point impact load based on higher－order shear deformation theory［J］.Composite Structures，2011，93(5):1474－1484.

［3］孙丹，罗松南.四边固支功能梯度板中波的传播［J］.振动与冲击，2011，30(4):244－247.SUN Dan， LUO Song－nam. Wave propagation in a rectangular functionally graded material plate with clamped supports［J］.Journal of Vibration and Shock，2011，30(4):244－247.

［4］Lefebvre J E，Zhang V，Gazalet J，et al.Acoustic wave propagation in continuous functionally graded plates:an extension of the Legendre polynomial approach［J］.Ultrasonics， Ferroelectrics and Frequency Control， IEEE Transactions on，2001，48(5):1332－1340.

［5］Cao X，Jin F，Jeon I.Calculation of propagation properties of Lamb waves in a functionally graded material(FGM)plate by power series technique［J］.NDT ＆ E International，2011，44(1):84－92.

［6］Patera A T.A spectral element method for fluid dynamics:laminar flow in a channel expansion［J］. Journal of Computational Physics，1984，54(3):468 －488.

［7］Palacz M，Krawczuk M.Analysis of longitudinal wave propagation in a cracked rod by the spectral element method［J］.Computers＆ Structures，2002，80(24):1809－1816.

［8］Kudela P，Krawczuk M，Ostachowicz W.Wave propagation modelling in 1D Structures using spectral finite elements［J］.Journal of Sound and Vibration，2007，300(1):88－100.

［9］Komatitsch D，Martin R，Tromp J，et al.Wave propagation in 2－D elastic media using a spectral element method with triangles and quadrangles［J］.Journal of Computational Acoustics，2001，9(2):703－718.

［10］Peng H，Meng G，Li F.Modeling of wave propagation in plate structures using three－dimensional spectral element method for damage detection［J］.Journal of Sound and Vibration，2009，320(4):942－954.

［11］Chakraborty A，Gopalakrishnan S.A spectrally formulated finite element for wave propagation analysis in functionally graded beams［J］.International Journal of Solids and Structures，2003，40(10):2421 －2448.

［12］Chakraborty A，Gopalakrishnan S.A higher－order spectral element for wave propagation analysis in functionallygraded materials［J］.Acta Mechanica，2004，172(1 －2):17 －43.

［13］Hedayatrasa S，Bui T Q， Zhang C， et al. Numerical modeling of wave propagation in functionally graded materials using time－domain spectral Chebyshev elements［J］.Journal of Computational Physics，2014，258:381－404.

［14］Chen W Q，Wang H M，Bao R H.On calculating dispersion curves of waves in a functionally graded elastic plate［J］.Composite Structures，2007，81(2):233 －242.

［15］Mažeika L，Draudvilien L，Žukauskas E.Influence of the dispersion on measurement of phase and group velocities of Lamb waves［J］.Ultrasound，2009，64(4):18 －21.

［16］Mažeika L，Draudvilien L.Analysis of the zero－crossing technique in relation to measurements of phase velocities of the Lamb waves［J］.Ultrasound，2010，66(2):7 －12.