基于辨识路面的矿用自卸车平顺性优化

朱一帆，谷正气，2，张 沙

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082;2.湖南工业大学，湖南 株洲 412007)

矿用自卸车是现代矿山的重要运输设备，属于非公路车辆，其常年运行在比较恶劣的矿山路面上，这对矿用自卸车的平顺性能提出了较高的要求。

对于矿山车辆，路面不平度是汽车行驶时最主要的激励［1］，准确路面信息的获取是进行车辆平顺性和操纵稳定性分析和评价的关键。近年来许多学者对路面不平度辨识进行研究，Castelnovi等［2］利用激光反射识别路面，通过激光发射和接收时间差，计算出路面粗糙度;王亚等［3］提出两种将单轮辙路面不平度时域模型拓展为双轮辙路面不平度时域模型方法;高建等［4］通过车轮减速时滑移率识别路面;Wang等［5］等利用轮胎动态压力传感器测量轮胎路面交互响应，对城市道路不平度进行估计;韩建保等［6］通过识别轮胎表面橡胶随时间的变形来识别路面;Ngwangwa等［7］将人工神经网络方法应用到路面不平度辨识问题中;Swart等［8］提出基于路面声波反射识别路面的方法。针对矿区路面的特殊性，很多路面不平度识别方法存在一定难度或缺陷，无法在工程实际中运用，因而需要进一步的研究。

本文结合以上学者的研究成果，提出利用遗传算法优化的BP神经网络由易于测量的座椅加速度辨识矿山路面不平度的方法。建立矿用自卸车刚柔耦合仿真模型，将仿真得到的座椅加速度作为网络理想输入样本，基于逆变换原理拟合出的路面不平度作为网络理想输出样本，通过网络训练，建立两者之间非线性映射模型。在整车道路试验验证辨识结果合理的基础上，利用多岛遗传算法对矿用自卸车油气悬架和座椅结构参数进行不确定性优化，平顺性得以改善。

1 矿用自卸车刚柔耦合模型建立

车架是矿用自卸车主要承载部分，其运动变形对自卸车整车性能评定影响很大，基于实际情况，进行整车建模时将车架处理为柔性体［9］。

在Solidworks中建立车架三维模型，导入Hypermesh中对其进行网格划分，考虑到真实车架模型非常复杂，需进行几何简化，并采用壳单元对其进行离散，设置不同的厚度值的单元属性来替代车架各不同厚度的钢板。车架各元件板厚主要为:筋板厚度为16mm，纵梁厚度为25mm，龙门梁厚度为30mm，车架吊耳厚度为50mm，与后牵引梁连接的纵梁以及前牵引梁厚度为45mm等。车架材料采用SUMITEN610F高强度低合金调质钢，具体参数如表1所示。

表1 车架材料参数Tab.1 Parameters of frame material

建立的车架有限元模型如图1所示，其中以四边形单元为主，但由于模型的复杂性，存在少量三角形单元进行过渡。

图1 车架有限元模型Fig.1 Finite element model of the frame

以Hypermesh为求解器，得到模态中性文件，经ADAMS处理即可生成柔性体车架。根据多体动力学原理，在ADAMS软件中建立自卸车其他系统模型，通过外部节点间接定义柔性车架与外部连接件的约束［10］。图2为在 ADAMS中建立的整车刚柔耦合模型。

图2 整车刚柔耦合模型Fig.2 Rigid-flexible vehicle model

其中，通过四个Bushing模拟座椅悬架刚度和阻尼特性。轮胎型号为40.00R57，其刚度阻尼参数通过米其林公司提供的试验拟合数据获取，将相关参数输入编制的轮胎tir文件，最后导入动力学模型。油气悬架的非线性刚度和阻尼曲线在matlab中编程拟合生成，如图3、图4所示，然后由Spline曲线导入模型中。

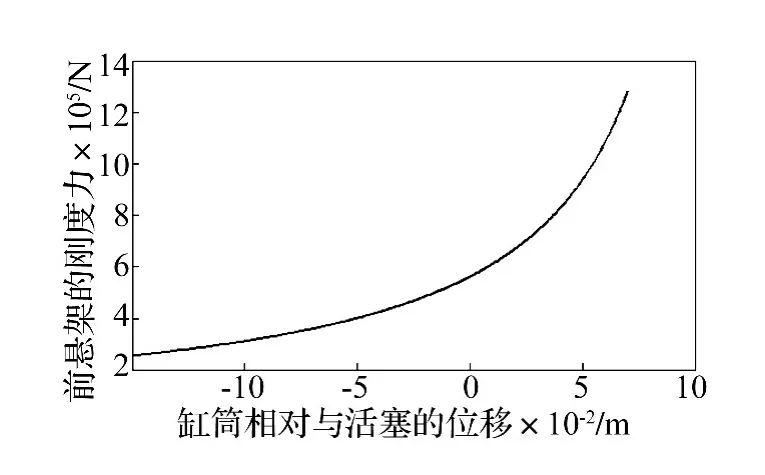
图3 前悬刚度特性曲线Fig.3 Front suspension stiffness characteristic curve

图4 前悬阻尼特性曲线Fig.4 Front suspension damping characteristic curve

2 BP神经网络路面辨识模型

BP神经网络是一种多层前馈网络，可以实现从输入到输出的任意非线性映射，具有较强的学习能力和容错鲁棒性［11］。对神经网络的设计主要包括网络结构模型设计、系统训练样本集获取、网络训练与测试。

2.1 BP网络结构模型设计

神经网络结构模型设计主要包括神经网络输入参数、输出参数、隐层数、隐层节点数以及网络参数的确定等［12］。网络结构如图 5 所示，h1m、h2n、h3q分别是神经网络的输入层、隐含层和输出层，xm为样本输入，yn为样本输出。

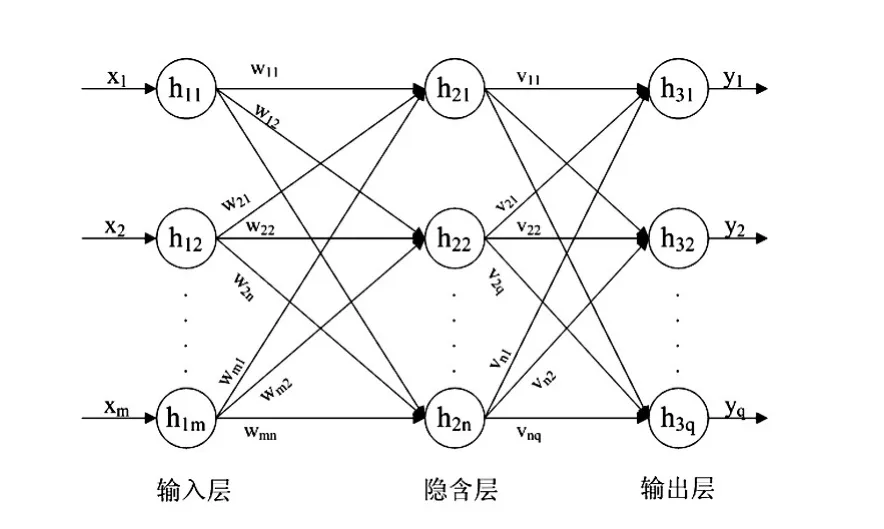
图5 BP网络结构图Fig.5 BP network structure

以座椅加速度作为该神经网络的输入参数，路面不平度作为输出参数。输入到输出层采用的是S形函数传递，其表达式为

其中:ai为输入层经过隐含层传递函数后的输出，ak为隐含层经过输出层传递函数后的输出，w和b分别为权值和阀值。

理论已经证明，具有一个 S形隐含层加上一个线性输出层网络，可以逼近任何有理函数［13］，故选取两层神经网络进行逼近。对于隐层神经元数目，经多次试验确定，选取为20个。

2.2 系统训练样本集的获取

自卸车运行路面为矿山路面，路面不平度主要集中在C、D、E三级范围内，将路面不平度系数Gq(n0)在500×10－6m3～5000×10－6m3范围内均匀取200个值，结合文献［14］利用逆变换的方法得到路面不平度xm随路面走向的曲线，作为网络理想输出样本。根据ADAMS中路面生成原理，编写VB路面谱程序生成rdf文件，通过图2刚柔耦合模型进行模拟仿真，得到相应的座椅加速度曲线，作为网络理想输入样本。在此共获得200组样本值，将其进行归一化处理，随机取其中190组进行训练，剩余10组用来测试。

2.3 BP网络训练方法

将网络实际输出z与期望输出y的均方差作为网络训练误差评价函数，如式(3)所示

式中:m和q分别为样本数及输出参数数目，zij和yij分别为第j个样本的第i个参数的实际输出和期望输出。应用附加动量及自适应学习率的学习算法来训练网络［15］。权值矩阵的迭代变化为

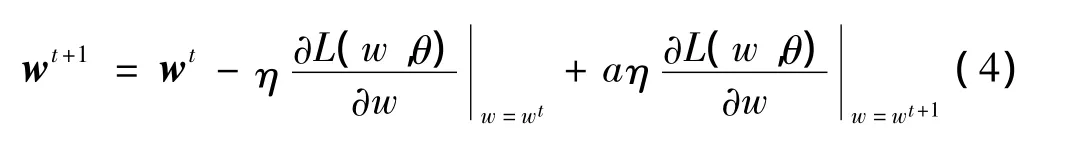
式中:a，η，t分别为动态因子、学习速率及迭代步数，wt+1和wt分别为第t+1及t个迭代对应的权值矩阵。

根据每迭代步误差L(w，b)是否降低，η进行相应改变，如果L(w，b)降低，则在下一步迭代步中η乘以1.01 的系数，否则，η 乘以0.99。

3 遗传算法优化

为了获得较好的初始权值和阈值，利用擅长全局搜索的遗传算法对BP神经网络的权值和阈值进行优化，可以有效辟免算法陷入局部极小值，提高收敛速度与精度［16］。图6为遗传算法优化BP网络流程图。

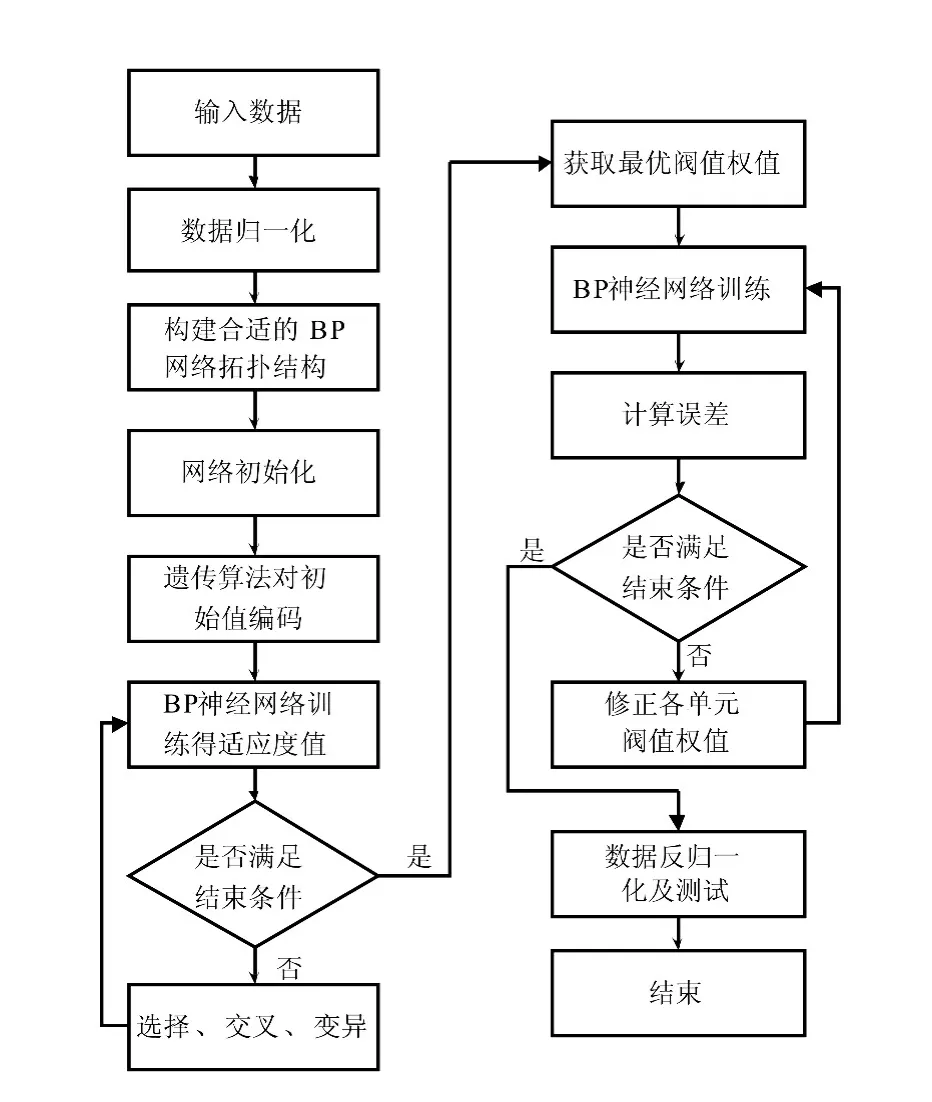
图6 遗传算法优化BP网络流程图Fig.6 Genetic algorithm optimized BP network flowchart

采用精度高的实数值编码方法，适应度函数为误差评价函数的倒数，对个体进行选择、交叉、变异等遗传操作处理，并遵循适者生存的原则，在潜在的解决方案种群中逐次产生一个近似最优的方案［17］，以此进行种群的进化，最终获得最优权值和阈值。

选择:个体i选择概率pi为

式中:Fi为个体i的适应度值，N为种群个体数。

交叉:采用实数交叉法对第i个染色体gi和第j个染色体gj在n位进行交叉操作，则交叉之后变为

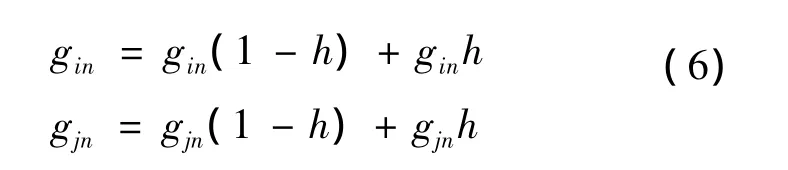
式中:h为［0，1］之间随机数。

变异:第m个个体的第n个基因amn变异操作方法如下

式中:v为一个随机数，u为当前迭代次数，Gmax是最大进化次数，gmin为基因 gmn的下限，gmax为基因 gmn的上限，r为［0，1］间的随机数。

4 GA-BP在路面辨识中的应用

4.1 辨识方法

将驾驶员座椅垂向加速度au作为输入样本，对应的路面不平度xm作为输出样本。采用第3节所述的遗传优化算法，取种群大小为30，进化代数为60次，交叉概率为0.4，变异概率为0.2。个体适应度进化过程如图7所示，当遗传算法进化到大约45代时，个体适应值趋于稳定，得到最优权值阀值。

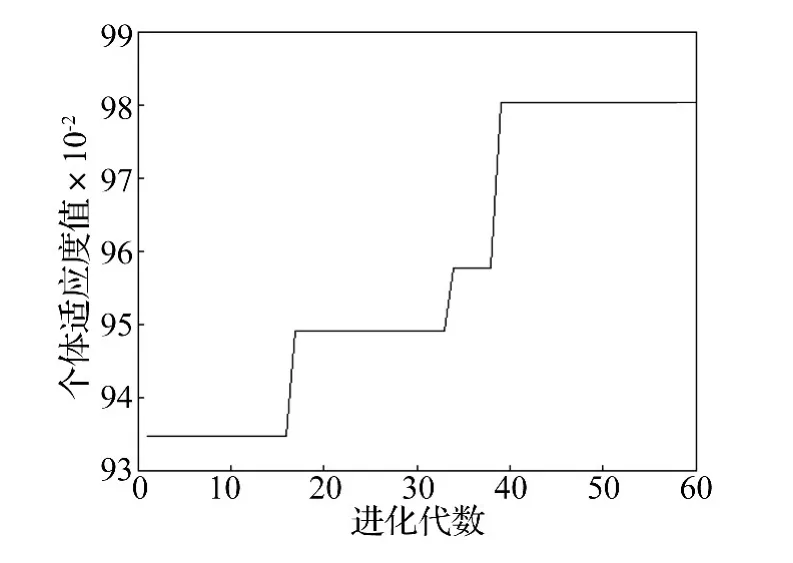
图7 个体适应度进化过程Fig.7 The evolution of individual fitness

对190组样本进行训练，建立驾驶员座椅加速度与路面不平度的非线性映射关系。对辨识路面xb从功率谱密度和路面不平度两方面进行对比分析，网络训练分析流程如图8所示。

4.2 辨识结果

图9～10给出了利用标准BP网络和遗传算法优化BP网络对D级路面辨识结果。其中R表示测试路面与辨识路面相关性系数，e表示相对误差值。图11为利用BP网络和GA～BP对10组测试样本进行路面不平度预测得出的相关系数及相对误差。从图9～11可看出，利用GA优化BP网络辨识路面与测试路面吻合度好，相关系数大约在97%左右，相对误差大约在2%左右，与标准BP网络辨识相比，预测精度提高，更加接近期望值。

图8 网络训练流程图Fig.8 Network training flowchart

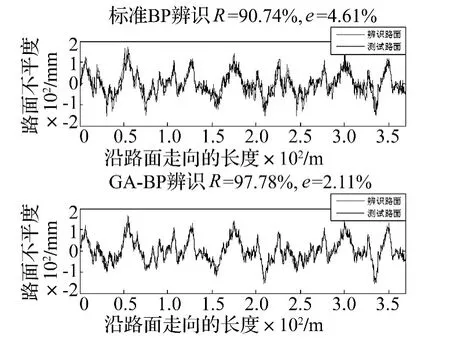
图9 D级路面不平度辨识结果Fig.9 Class D road roughness identification results

图10 D级路面功率谱密度辨识结果Fig.10 Class D power spectral density of the identification result

4.3 试验验证

为了验证GA-BP神经网络辨识路面的准确性，在矿区实际路面上对自卸车进行了不同试验车速下(10 km/h，20 km/h，30 km/h)整车满载道路行驶试验，如图12所示。

图11 路面不平度预测相关系数及相对误差Fig.11 Road roughness prediction correlation coefficient and the relative error

图13为试验得到的30 km/h车速下驾驶室座椅垂向加速度，将其作为输入样本代入已训练好的GA-BP神经网络进行计算，得辨识矿山路面的不平度如图14所示，将该辨识路面导入图2所示自卸车刚柔耦合模型，得到座椅垂向加速度仿真值，如图15所示。

图12 矿用自卸车满载道路试验Fig.12 Fully loaded dump truck road test

可以清楚地看出，试验与仿真得出的座椅垂直方向加速度波动范围一致，均为 －2.0 m/s2～2.0 m/s2。将上述两组座椅垂直方向加速度数据导入adams后处理中进行FFT变换得到加速度功率谱密度曲线，如图16所示。仿真结果与试验结果基本吻合，频率成分都集中在低频，峰值为 0.187 m2/(Hz·s4)与 0.196 m2/(Hz·s4)，验证了辨识结果的准确性。

图13 试验座椅垂向加速度响应Fig.13 Vertical acceleration response of test seat

图14 矿山路面不平度辨识结果Fig.14 Mine road roughness identification results

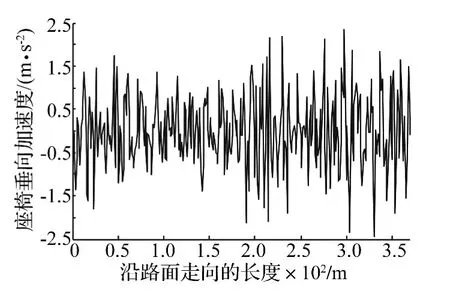
图15 座椅垂向加速度仿真结果Fig.15 Seat vertical acceleration simulation results

图16 仿真与试验加速度功率谱密度曲线Fig.16 Simulation and test acceleration power spectral density curve

表2是驾驶室座椅不同车速下三个方向加速度均方根仿真值与实验值对比(X为行驶方向、Y为自卸车横向、Z为垂向)。其中仿真路面分别为辨识路面与矿用车仿真常用C级、D级路面。可以看出，座椅垂向加速度的辨识路面仿真结果更加接近实验值，与C级、D级路面仿真结果比较，精度提高约12.3%，且对于X、Y方向，辨识路面仿真结果与实验值比较接近，进一步验证了辨识路面的可靠性，因此辨识路面能更加真实反应实际矿山路面，提高了模型的建模精度。但由表2可以看出，座椅振动加速度垂直方向均方根值偏大，根据文献［18］判断出人体主观感觉为相当不舒适，故需对自卸车减振系统进行优化。

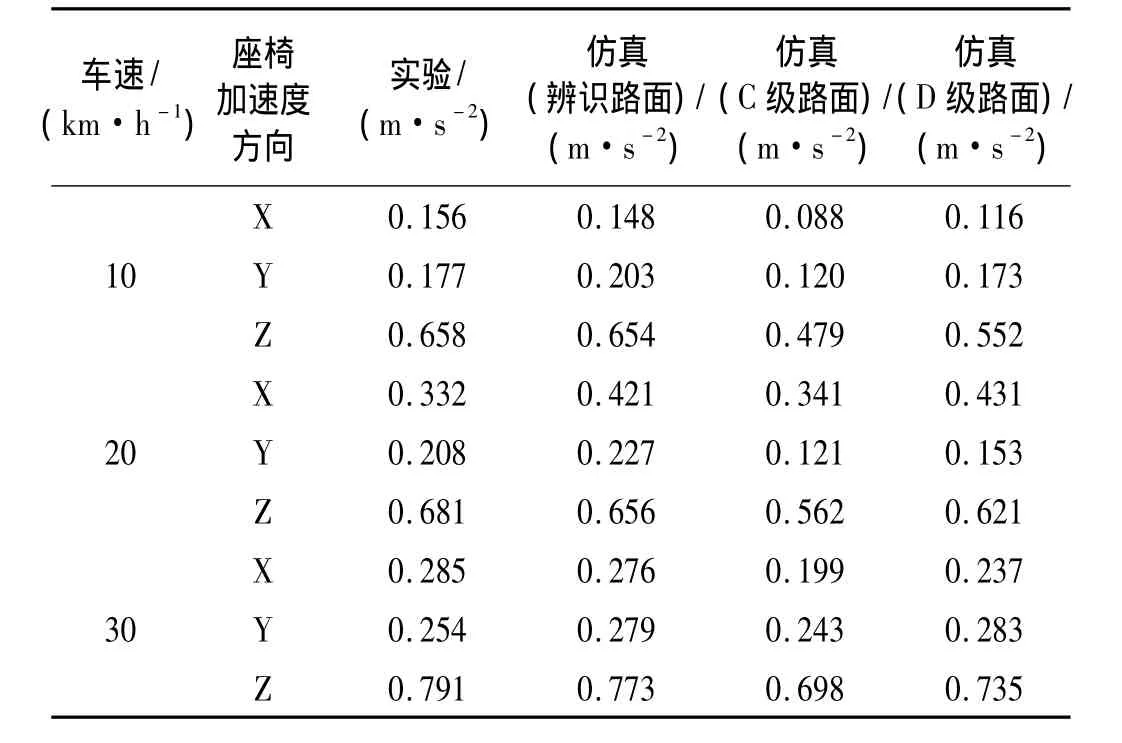
表2 座椅加速度均方根值仿真与实验对比Tab.2 Seat acceleration rms value comparison of simulation and experimental

5 平顺性不确定性优化

矿用自卸车载货吨位较大，且其装载方式具有很大随机性，导致自卸车簧载质量易发生较大变化，轮胎的气压和车辆行驶速度会直接导致轮胎刚度和阻尼的变化，簧载质量和轮胎刚度阻尼可视为不确定性变量，其耦合在一起对系统响应产生显著影响。本文进行平顺性优化时考虑了上述不确定因素，借助多岛遗传算法对油气悬架和座椅参数进行优化。

5.1 优化变量和不确定性量

对油气悬架非线性刚度和阻尼特性影响较大的为其阻尼孔直径和充气高度［19］，故选取前后悬架的充气高度hf、hr，阻尼孔直径df、dr以及座椅刚度k与阻尼c组成六维优化变量X。将自卸车运行过程中变化较大的轮胎刚度kt、阻尼ct及簧载质量M选取为三维不确定变量U。优化变量与不确定变量的取值范围如表3、表4所示。

表3 各优化变量取值范围Tab.3 Each range of optimization variables

表4 不确定变量取值范围Tab.4 Range of uncertain variables

5.2 目标函数和约束条件

根据ISO2631－1:1997(E)标准，将座椅三个轴向的总加权加速度a最小作为平顺性评价目标函数，由于存在不确定量U，故不确定目标函数表达式为:

其中:av为三个轴向的总加权加速度均方根值，avx，avy，avz分别为纵向、侧向、垂向加权加速度均方根值。

针对任一组优化变量X，因为存在不确定量U，且αv为 U的连续函数，故 αv可能取值范围为区间［amix(X)amax(X)］，其中 amin(X)，amax(X)分别为 αv在不确定变量U上的最小与最大取值。进行不确定性优化的关键是将不确定性目标函数转换为确定性目标函数。故本文将式(9)不确定性目标函数转化为确定性目标函数，即:

自卸车在行驶过程中的侧倾和俯仰运动对行驶稳定性影响较大，为保证汽车的正常行驶，要求车身侧倾角不超过6°～7°，车身的俯仰角小于1°～3°，且悬架动挠度fd和车轮相对动载荷Fd在适当的范围内变化。

式中:σfd与σFd分别为悬架动挠度与车轮相对动载荷均方根值，［fd］为悬架动挠度的许用值，取15。

5.3 不确定性优化

根据优化拉丁方法确定60组优化变量和不确定变量样本，通过基于辨识路面的ADAMS刚柔耦合模型仿真分析，得到总加权加速度均方根值αv，根据以上60组样本点和响应值建立优化变量和不确定变量与座椅加速度响应的Kriging近似模型。任取两组采样样本进行仿真分析，近似模型的相对误差见表5，该模型误差小于2.5%，可以用于后续的不确定优化。

表5 近似模型验证Tab.5 Approximate model validation

基于以上建立的近似模型，借助多岛遗传算法，以式(10)为目标函数，式(11)为约束条件，对座椅参数和油气悬架进行优化设计。优化时遗传算法操作参数如下:种群40，代数200，岛数为10，交叉概率 0.8，变异概率0.03，经优化得到座椅与油气悬架参数如表6所示。

表6 优化后悬架和座椅参数Tab.6 The optimized parameters of suspension and seats

5.4 优化结果分析

图17是自卸车模型以30 km/h在辨识路面仿真得到座椅加速度时域与频域响应优化前后结果对比。

图17 优化前后平顺性结果对比Fig.17 Results contrast of before and after optimization

从图17中可清楚地看出，优化后的座椅时域加速度响应显著降低，经计算均方根由0.773 m/s2降为0.484 m/s2，下降了37.4%，功率谱密度的峰值减小了0.033 m2/(Hz·s4)，从而提高了矿用自卸车的平顺性，改善了矿用自卸车的乘坐舒适性。

6 结论

(1)本文结合矿用自卸车整车刚柔耦合模型，利用GA-BP神经网络由便于测量的座椅加速度对矿山路面不平度进行了有效辨识，该方法操作简单、易于实现。与标准BP网络相比，遗传算法的优化提高了网络的预测能力。

(2)通过整车满载道路行驶试验，确定辨识的矿山路面不平度的可信性。辨识路面和C级、D级路面的仿真结果对比表明，辨识路面能更加真实模拟实际矿山路面，对提高建模精度具有重要的实际意义。

(3)以辨识矿山路面作为路面激励，通过多岛遗传算法对油气悬架和座椅结构参数进行不确定性优化研究，优化后座椅垂直加速度均方根值下降了37.4%，平顺性得到很大改善。

［1］段虎明，石峰，谢飞，等.路面不平度研究综述［J］.振动与冲击，2009，28(9):95－101.DUAN Hu-ming，SHI Feng，XIE Fei，et al.A survey of road roughness study［J］.Journal of Vibration and Shock，2009，28(9):95－101.

［2］Castelnovi M，Arkin R，Collins T R.Reactive speed controlsystem based on terrain roughness detection［C］//Robotics and Automation，2005.ICRA 2005.Proceedings of the 2005 IEEE International Conference on.IEEE，2005:891－896.

［3］王亚，陈思忠，郑凯锋.时空相关路面不平度时域模型仿真研究［J］.振动与冲击，2013，32(5):70－74.WANG Ya，CHEN Si-zhong，ZHENG Kai-feng.Simulation research on time domain model of road roughness with timespace correlation［J］.Journal of Vibration and Shock，2013，32(5):70－74.

［4］高建，殷承良，张勇，等.基于路面自动识别的ABS自适应神经模糊控制器仿真研究［J］.汽车技术，2006，6:4－7.GAO Jian，YIN Cheng-liang，ZHANG Yong，et al.The simulation research of ABS self-adapting nerve fuzzy control unit base on road automatic identification［J］.Automobile Technology，2006，6:4－7.

［5］Wang Q，McDaniel J G，Sun N X，et al.Road profile estimation of city roads using DTPS［C］//SPIE Smart Structures and Materials+ Nondestructive Evaluation and Health Monitoring.International Society for Optics and Photonics，2013:86923C －86923C －8.

［6］韩建保，张鲁滨，李邦国.轮胎路面附着系数实时感应识别系统［J］.车辆与动力技术，2005，2:62－64.HAN Jian-bao，ZHANG Lu-bin，LI Bang-guo.Electronic sensing system for realTime identification of the tire-road adhesion［J］.Vehicle ＆ Power Technology，2005，2:62－64.

［7］Ngwangwa H M，Heyns P S，Labuschagne F J J，et al.Reconstruction of road defects and road roughness classification using vehicle responses with artificial neural networks simulation［J］.Journal of Terramechanics，2010，47(2):97－111.

［8］Swart P L，Lacquet B M，Blom C.An acoustic sensor system for determination of macroscopic surface roughness［J］.Instrumentation and Measurement，IEEE Transactions on，1996，45(5):879－884.

［9］杨明亮，徐格宁.基于约束刚柔耦合系统的叉车振动研究［J］.机械工程学报，2011，47(20):89－94.YANG Ming-liang，XU Ge-ning.Vibration study of fork-lift truck based on the constraint-rigid-flexible coupling System［J］.Journal of Mechanical Engineering，2011，47(20):89－94.

［10］宋桂霞.汽车钢板弹簧柔性体建模与仿真研究［J］.农业装备与车辆工程，2011，6:008.SONG Gui-xia.Flexible body modeling and simulation study on automobile leaf spring［J］.Agricultural Equipment ＆Vehicle Engineering，2011，6:008.

［11］陈建政，林建辉.在线连续测量轮轨接触点的神经网络方法［J］.振动与冲击，2007，26(5):90－92.CHEN Jian-zheng， LIN Jian-hui. Online continuous measurement of rail wheel contact point based on neuro network method［J］.Journal of Vibration and Shock，2007，26(5):90－92.

［12］韩利芬，高晖，李光耀，等.神经网络与遗传算法在拉延筋参数反求中的应用［J］.机械工程学报，2005，41(5):171－176.HAN Li-fen，GAO Hui，LI Guang-yao，et al.Application of neural network and genetic algorithm to inverse solution of parameters of drawbead［J］. Journal of Mechanical Engineering，2005，41(5):171－176.

［13］钱立军，袭著永，赵韩.基于BP神经网络的发动机排放预测［J］.汽车工程，2005，27(1):28－30.QIAN Li-jun，XI Zhu-yong，ZHAO Han.Engine emissions prediction based on back propagation neural network［J］.Automotive Engineering，2005，27(1):28－30.

［14］刘献栋，邓志党，高峰.基于逆变换的路面不平度仿真研究［J］.中国公路学报，2005，18(1):122－126.LIU Xian-dong， DENG Zhi-dang，GAO Feng. Study of simulation of road roughness based on inverse transform［J］.China Journal of Highway and Transport，2005，18(1):122－126.

［15］Xu D，Yap F F，Han X，et al.Identification of spring-force factors of suspension systems using progressive neural network on a validated computer model［J］.Inverse Problems in Engineering，2003，11(1):55－74.

［16］吴仕勇.基于数值计算方法的BP神经网络及遗传算法的优化研究［D］.昆明:云南师范大学，2006.

［17］琚亚平，张楚华.基于人工神经网络与遗传算法的风力机翼型优化设计方法［J］.中国电机工程学报，2009(20):106－111.JU Ya-ping，ZHANG Chu-hua.Optimal design method for wind turbine airfoil based on artificial neural network model and genetic algorithm［J］.Proceedings of the CSEE，2009(20):106－111.

［18］余志生.汽车理论［M］.北京:机械工业出版社，2009.

［19］向华荣.基于油气悬架的车辆平顺性研究［D］.南京:江苏大学汽车交通工程学院，2005.