主轴－刀柄－刀具系统刀尖频响函数的预测方法研究

王二化，吴 波，胡友民，王 军，杨叔子

(1.常州信息职业技术学院 机电工程学院，江苏 常州 213164;2.华中科技大学 数字制造装备与技术国家重点实验室，武汉 430074)

为保证切削过程的稳定性，通常用稳定性Lobe图来确定切削过程中稳定和不稳定的切削区域，而稳定性Lobe图的绘制需要首先获取机床的动力学知识(刀尖频响函数)。刀尖频响函数可以通过激振实验方法获得［1－2］，但对于大量主轴、刀柄和刀具组合来说，需要对每一种组合重复相同的实验，在生产实际中很难实现。为了解决这个问题，美国标准和技术研究院Schmitz等［3－4］提出了动柔度耦合子结构分析方法(RCSA)，接着，一些研究人员［5－7］对其进行了一些改进。在这些刀尖频响函数预测模型中，一般通过模态叠加法计算刀柄和刀具端点频响函数，这种方法有两个方面的缺陷:① 引入模态误差，降低子结构端点频响函数精度;② 模态叠加法计算量较大，影响预测效率。

本研究是在课题组胡峰、吴波等相关研究基础上［8－9］，针对模态叠加法中出现的问题，本研究以Timoshenko梁理论、传递矩阵法和RCSA耦合技术为基础，提出了一种新的刀尖频响函数预测方法。由于避免了大量复杂的模态分析，该算法在精度和效率方面都具有较大优势，有助于快速地得到高精度的刀尖频响函数，为保证切削过程的稳定提供必要的理论依据和技术支持。

1 基于Timoshenko梁的传递矩阵理论

在结构动力学分析中，常用的梁结构包括欧拉－伯努利梁和Timoshenko梁两种形式。欧拉－伯努利梁适用于高度远小于跨度的细长结构，但对于跨度长度比较小的结构，计算精度就很难满足实际需要。针对主轴、刀柄和刀具结构特点，利用考虑剪切变形和转动惯量的Timoshenko梁理论［10］建立各子结构动力学模型，根据参考文献［11－12］，作者通过单段Timoshenko梁运动学方程和动平衡条件计算各子结构左右两端截面之间的传递矩阵。

1.1 单段Timoshenko梁的传递矩阵

以两端自由的Timoshenko梁段作为研究对象，计算其左右两端的传递矩阵，梁段如图1所示。

图1 Timoshenko梁模型Fig.1 Timoshenko beam model

Timoshenko梁段的运动方程如下所示

其中:y(x，t)为梁上任一点的瞬时位移;A是梁段横截面积;m为单位长度的梁段质量;E是杨氏弹性模量(假设各向同性);G是剪切模量;k是剪切系数;I是二阶截面惯性矩，l为梁段长度，Mi－1，Qi－1分别为梁段左端面的弯矩和剪切力，Mi，Qi分别为梁段右端面的弯矩和剪切力。

两端自由Timoshenko梁段的动平衡方程为

根据Timoshenko梁段运动和动平衡方程，可以推导出梁段左截面状态矢量为

同样，梁段右端面的状态矢量为

其中，矩阵T1和T2如表达式(3)和(4)所示，可得梁段左端面和右端面之间的关系如下

因此，可得两端自由Timoshenko梁段左端面和右端面之间的传递矩阵如下所示。

1.2 弹性支撑元件的传递矩阵

在主轴建模过程中，除了两端自由Timoshenko梁左右端面之间的传递矩阵外，还需考虑轴承等弹性支撑元件左右端面的传递矩阵。本节以等效刚度ky和等效粘性阻尼系数cy支撑的无质量Timoshenko梁段为研究对象，分析其受力情况，如图2所示。

图2 弹性支撑结构及其受力分析图Fig.2 Structure and the force analysis diagram of elastic supporting

其中:Mi－1和Mi分别为施加在弹性支撑左端面和右端面上的弯矩;Qi－1和Qi分别为弹性支撑左端面和右端面上的剪切力;yi－1为弹性支撑左端面上的直线位移;ω是角频率。根据平衡和兼容条件，弹性支撑左右端面的位移、转角、弯矩和剪力之间的关系如下所示

弹性支撑左右端面状态矢量的传递矩阵为

2 建立刀尖频响函数预测模型

如上所述，本研究利用多段Timoshenko梁建立主轴、刀柄和刀具模型，并通过传递矩阵法计算各子结构端点频响函数，最后利用RCSA法耦合各子结构预测刀尖频响函数。

2.1 获取各子结构端点频响函数

通过上述Timoshenko梁和弹性支撑元件的传递矩阵理论，获取各子结构左右端面总体传递矩阵，并通过适当变换，计算各子结构端点频响函数。

首先定义子结构端点频响函数H，N，L和P如下

其中:y和θ分别为子结构端点直线位移和角位移;f和m分别为作用在端点0和k上的力和弯矩。

以主轴为研究对象，利用多段Timoshenko梁理论和弹簧阻尼单元建立主轴动力学模型如图3所示。

图3 弹簧和阻尼支撑的主轴动力学模型Fig.3 Dynamic model of the spindlesupported by springs and dampers

其中:kyf和cyf分别为主轴前轴承的直线刚度和阻尼;kyr和cyr分别为主轴前轴承的直线刚度和阻尼;0，1，2，…，11代表多段 Timoshenko梁的各个截面;［T1］，［T3］，…，［T8］，［T10］，［T11］分别表示分布质量梁段左右端面状态矢量传递关系，［T2］和［T9］表示弹性支撑单元的传递矩阵。

通过单段Timoshenko梁和弹性支撑单元传递矩阵计算方法，可得主轴子结构的整体传递关系如下所示

为了计算主轴端点频响函数，将0点到11点状态矢量的传递方程修改为

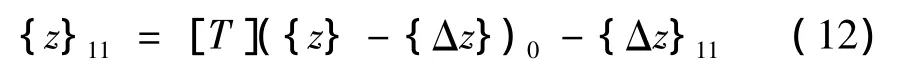
为了获取刀尖频响函数H00和N00，方程(12)可以简化为

方程(13)的后两个表达式如下所示

刀尖频响函数H00和N00可以得到

利用相似的方法，刀尖频响函数 L00和 P00可以得到

利用同样的方法，可以得到剩余的12个刀尖频响函数。

主轴端点频响函数矩阵可以表示如下

同样利用多段Timoshenko梁建立刀柄和刀具动力学模型，如图4所示。

图4 刀柄和刀具动力学模型Fig.4 Dynamic model of the holder and tool

其中:0，1，2，…，6等分别为各段 Timoshenko梁端面，［T1］，［T2］，［T3］，…，［T6］等分别为各段 Timoshenko梁左右端面之间的传递矩阵。

利用和计算主轴端点频响函数相似的方法，可以得到刀柄和刀具端点频响函数，其频响函数矩阵分别为

2.2 RCSA子结构耦合理论

得到主轴、刀柄和刀具三个子结构的端点频响函数矩阵后，利用RCSA方法获取主轴－刀柄－刀具系统的刀尖频响函数［7］，三部件耦合结构如图5所示。为了获得更加精确的刀尖频响函数，主轴－刀柄与刀柄－刀具之间结合面直线与转动刚度和阻尼均需考虑。为了建立一个更加真实的模型，主轴中的刀柄部分看成是主轴的一部分，刀柄中的主轴部分看成是刀柄的一部分。

图5 主轴、刀柄和刀具的弹性耦合结构Fig.5 Elastic coupling structure of the spindle，holder and tool

主轴－刀柄结合面动力学的复刚度矩阵可以表示如下

利用RCSA方法，主轴－刀柄耦合系统SH端点频响函数如下所示

得到主轴－刀柄耦合系统SH端点频响函数后，利用相似的方法，主轴－刀柄－刀具系统的端点频响函数矩阵可以得到。装配体刀尖频响函数矩阵的第一个元素如下所示［7］

其中:Kht是刀柄－刀具结合面的复刚度矩阵，如下所示

3 案例研究和讨论

3.1 刀尖频响函数计算

为了论证本研究提出的刀尖频响函数预测方法，本章选择参考文献［7］使用的案例进行刀尖频响函数预测研究，本案例使用的主轴－刀柄－刀具系统如图6所示。

图6 案例研究的各子结构及其装配体Fig.6 Each substructure and the assembly of case study

选择钢作为主轴，刀柄和刀具的材料，密度ρ=7800 kg/m3，杨氏模量 E=200GPa，泊松比 v=0.3。轴承、结合面动态参数及主轴、刀柄和刀具结构尺寸如表1～3所示。

表1 轴承及各结合面平均动态参数Tab.1 Average dynamic parameters of the bearing and interfaces

表2 轴承距主轴右端面的距离Tab.2 Distancesofthebearings fromtherightendofthespindle

表3 子结构尺寸:(1)主轴，(2)刀柄，(3)刀具Tab.3 Substructuredimensions:(1)spindle;(2)holder;(3)tool

其中，各子结构梁段都是从图形右边开始编号，刀具悬臂长度为85mm。

根据本案例提供的各子结构尺寸、轴承、结合面动态参数，利用本研究提出的刀尖频响函数预测方法，计算主轴－刀柄－刀具系统刀尖频响函数。研究发现，在刀尖频响函数计算过程中，需要进行大量的矩阵运算，因此，选择擅长矩阵运算的大型工程软件MATLAB实现本研究提出的算法［13］。

通过RCSA耦合方法，利用弹簧阻尼单元将主轴、刀柄和刀具三个子结构耦合起来，可以得到刀尖频响函数如图7所示。

由图7可以看出，在感兴趣的频带(0～4000Hz)范围内有七阶模态，前两阶刚体模态固有频率分别为71.6Hz和196.1Hz，它们主要取决于主轴的尺寸，支撑方式和支撑位置。其它模态都是弹性模态，它们主要受主轴－刀柄和刀柄－刀具结合面参数控制。

3.2 有限元仿真验证

图7 主轴－刀柄－刀具系统刀尖频响函数:幅值和相位图Fig.7 ToolpointFRFofthespindle－holder－tool system:magnitudeandphasediagrams

为了验证本文提出的计算方法，利用有限元软件ANSYS12.0建模给定的主轴、刀柄和刀具组合，通过有限元分析方法获取主轴－刀柄－刀具系统的刀尖频响函数［14－15］。在这个有限元模型中，Timoshenko梁单元Beam188用来建模给定组合的每个子结构，Beam188梁单元具有两个结点，并且每个结点能处理六个自由度。轴承、主轴－刀柄和刀柄－刀具结合面的动态特征利用ANSYS12.0的弹簧阻尼单元进行模拟。给定的主轴－刀柄－刀具组合的有限元、文献［7］和本文分析结果，及误差百分比如表4所示。

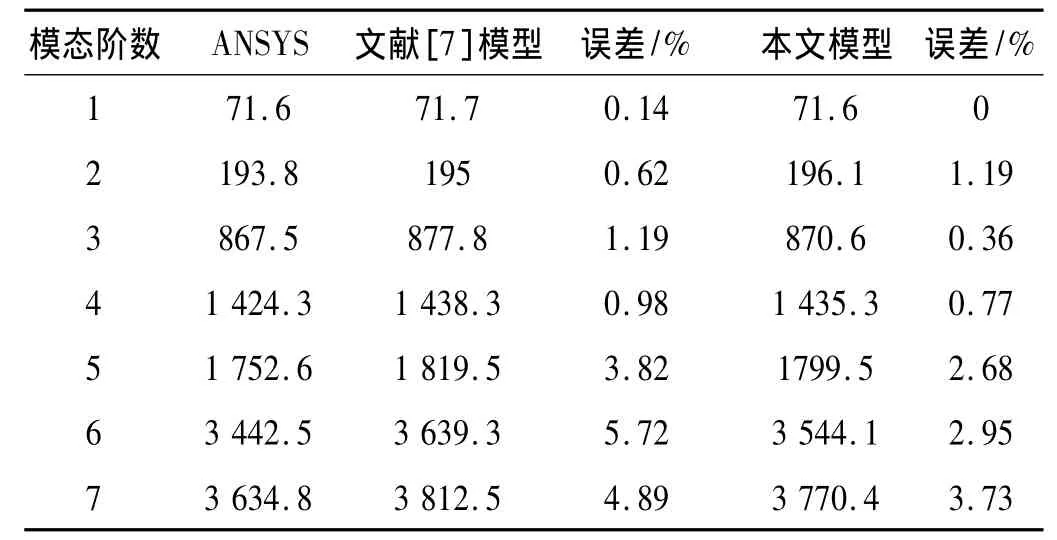
表4 案例研究中装配体的固有频率Tab.4 Naturalfrequencyofthe assemblyinthiscasestudy

由表4可以看出，本研究提出的刀尖频响预测方法与有限元结果一致性较好，前七阶模态最大误差不超过3%，除第二阶模态固有频率精度稍差外，其它几阶模态固有频率精度都明显优于参考文献［7］提出的计算方法。

利用指定的计算机(Pentium®Dual－CoreCPU2.93 GHz，2.0 GB RAM)，通过有限元模型计算给定组合刀尖频响函数(频段:0～4000 Hz，频率增量:0.5 Hz)需要30 min。然而，在同一台计算机上，通过本文提出的理论模型计算给定组合刀尖频响函数仅需30 s，而利用文献［7］提出的预测模型大约需要45 s，可以看出，本文提出的分析方法大大减少了计算时间，这主要因为避免了有限元模型和文献［7］中大量的模态分析，此外，由MATLAB软件实现的传递矩阵法能直接求解装配体的频响函数，省去了在有限元分析方法中大量的建模和网格划分时间。

4 结论

本研究结合Timoshenko梁理论、传递矩阵法和子结构耦合方法，提出了一种主轴－刀柄－刀具系统刀尖频响函数预测模型。比较有限元、文献［7］和本文提出的理论模型计算结果，可以发现，和文献［7］建立的刀尖频响函数预测模型相比，本文提出的理论模型在精度和效率方面都具有明显优势。本研究提出的刀尖频响函数预测方法有助于快速地得到高精度的立式铣床刀尖频响函数［16］，为保证切削过程的稳定提供必要的理论依据和技术支持。

［1］Budak E，Altintas Y.Analytical prediction of chatter stability in milling－Part I:general formulation;Part II:application to common milling systems［J］.Transactions of ASME，Journal of Dynamic Systems，Measurement，and Control，1998，120:22－36.

［2］Kivanc E B，Budak E.Structural modeling of end mills for form error and stability analysis［J］.International Journal of Machine Tools and Manufacture，2004，44(11):1151－1161.

［3］Schmitz T.Predicting high－speed machining dynamics by substructure analysis［J］.CIRP Ann.，2000，49(1):303－308.

［4］Schmitz T，Davies M，Kennedy M.Tool point frequency response prediction for high－speed machining by RCSA ［J］.Journal of Manufacturing Science and Engineering，2001，123:700－707.

［5］Park S S，Altintas Y，Movahhedy M.Receptance coupling for end mills［J］.International Journal of Machine Tools ＆Manufacture，2003，43:889－896.

［6］Schmitz T，Duncan G S.Three－component receptance coupling substructure analysis for tool point dynamics prediction［J］.Journal of Manufacturing Science and Engineering，2005，127:781－790.

［7］Ertürk A，Özgüven H N，Budak E.Analytical modeling of spindle－tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF［J］.International Journal of Machine Tools＆Manufacture，2006，46:1901－1912.

［8］胡峰，吴波，胡友民，等.基于概率神经网络和KS检验的机械状态监测［J］.振动与冲击，2008，27(4):56 －62.HU Feng，WU Bo，HU You－min，et al.Machine condition monitoring based on probabilistic neural network and KS inspection［J］.Vibration and Shock，2008，27(4):56 －62.

［9］胡峰，吴波，胡友民，等 利用粒子群优化算法实现阻尼和频率的精确识别［J］.振动与冲击，2009，28(7):8－11.HU Feng，WU Bo，HU You－min，etal.Precise identification of damping and frequency by using particle swarm optimization［J］.Vibration and Shock，2009，28(7):8－11.

［10］Timoshenko S P.On the correction for shear of the differential equation for transverse vibrations of prismatic bars［J］.Philosophical Magazine，1921，41:744－746.

［11］包世华.结构动力学［M］.武汉:武汉理工大学出版社，2005.

［12］杨肃，唐恒龄，廖伯瑜，等.机床动力学(Ⅱ)［M］.北京:机械工业出版社，1983.

［13］楼顺天，刘小东，李博菡.基于MATLAB7.X的系统分析与设计［M］.西安:西安电子科技大学出版社，2005.

［14］Cook，Robert D.Concepts and applications of finite element analysis［M］.Newyork:Wiley，2001.

［15］薛风先，胡仁喜，康士廷，等.机械与结构有限元分析［M］.北京:机械工业出版社，2010.

［16］王二化，吴波，胡友民，等.主轴－刀柄和刀柄－刀具结合面参数辨识研究［J］.振动与冲击，2014，33(10):50－54.WANG Er－hua，WU Bo，HU You－min，et al.Parameter identification of spindle－holder and holder－tool interfaces［J］.Journal of Vibration and Shock，2014，33(10):50－54.