放回还是不放回

陈志伟

“这样做不公平！应该你抽完再放回去，让我抽.否则，我不抽.”还没有走进教室，就能听到班长瑶瑶在吼.怎么回事？带着疑问，陈老师进了班级，看到班长、数学科代表和团支部书记正围在讲台上抽签.

班长看到陈老师进来就带着委屈告之事情的缘由，原来他们在用抽签的方法决定谁做这次班会课的主持人.

瑶瑶说：“不让我做主持人可以，但不要用这样的方法来欺负我.”

陈老师说：“你们是怎么抽的啊？”

瑶瑶说：“数学科代表制作了3个标签，其中一个上面写着主持人，每人抽一个，他先抽，团支部书记和我顺着来，谁抽到就谁当.”

陈老师问：“你觉得不公平，那么你认为应该如何抽？”

“我觉得应该他抽完，放回去.我们再接着抽，这样才公平.”

“同学们，现在班委遇到了问题，我们大家一起来看看，能不能帮助他们.”陈老师终于明白了他们争吵的原因.

同学们经过一段时间的思考，也分成了两派，一派支持数学科代表，一派支持班长瑶瑶.陈老师也看出了他们对这个问题的认识程度.支持的和不支持的都不能说服对方.

“好，我们前面学习了古典概型和几何概型，现在他们遇到的问题在于抽到的签是否放回以及抽签的顺序.是否放回影响不影响概率？如果影响，应该选择哪种方式公平？我们就结合前面所学习的概率内容进行探讨.在讲解之前，我们还是按照他们双方的方式，去做一次，看看最终的结果分别怎样？”

于是，大家就分组进行实验，结果很快出来了.不放回的组：有的第一个人抽到了，后面的人就不抽了；有的第二个人抽到的；有的第三个人抽到的.放回的组：有的只有一个人抽到了；有的有两个人都抽到了；有的三人都抽到了.这下大家都犯难了，他们是明显感受到了放回的有问题，但他们解释不了原因.

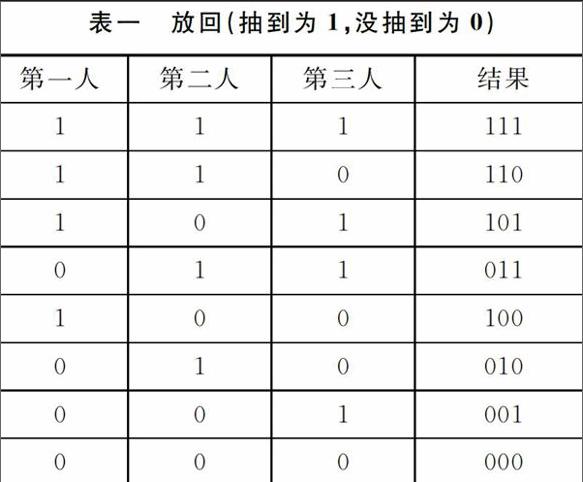
陈老师让同学们把两种问题的所有事件都用表格列出来.

从表一中，可以看出明显错误，因为只有一个人来做主持人，而上面的结果可能出现多个人做主持人的情况，不能解决问题.

从表二中，可以看出，这是可行的，每个人抽到的概率都是相等的，每个人抽中的概率都是

，每个人抽中与抽取的顺序没有关系，当3人抽取结束后，仅有一人抽中.

瑶瑶不服气说：“我看出放回是有问题的了，但是要是按照不放回抽签的话，第一个人抽到了，那么后面的两个人不用抽都知道不可能抽中了，那对后面的人不是不公平吗？那不是说谁先抽，就占便宜了吗？”

数学科代表说：“要是第一个人没有抽中，那第二个人抽不是概率变成

了吗？要是第一个人和第二个人都没有抽中，第三人抽的概率不是1了吗？不是先抽就高，最后一个人抽才高呢！”

陈老师笑着说：“从你们的分析看，你们目前还不能理解抽取没有顺序之分.你们觉得是否抽中，要看前面的人是否抽中，这就对了.实际上，不放回抽签，不能单单看某个个人在抽取时的抽中概率，而要看你在抽取过程中，整个事件的发生的概率.如果孤立地看待抽签，你会发现自己抽中与否是不公平的.这是一个条件概率的问题.从表二中我们可以看到，第一人没有抽中的概率是 ，第二人抽中的概率变成了 ，所以第二人最终抽中的概率是

；第三人抽中的概率要这样看，第一人没有抽中的概率是 ，第二人没有抽中的概率是 ，第三人抽取时，就一张签，是必然事件，故第三人最终抽中的概率是

，

“从整个事件可以看出，我们在做概率问题时，要分清楚抽取是不是放回，放回实际是一个N次独立事件的问题，概率与前面的事件发生概率无关；不放回是一个条件概率问题，后面事件发生的概率与前面事件的发生概率有关系.