指定频带简谐激励下约束阻尼结构拓扑优化

房占鹏，郑 玲，唐重才

(重庆大学 机械传动国家重点实验室，重庆 400044)

在航空航天领域，为减轻结构质量大多采用薄板类构件，因而导致振动噪声问题。约束阻尼处理技术能有效抑制结构宽频振动噪声，由于对原结构改变少，易于实施，广泛用于轻型结构的减振降噪。约束阻尼材料通常覆盖整个结构表面，不仅增加结构的附加质量，且不利于约束阻尼材料的高效利用。由于结构动力学拓扑优化获得长足进步，为约束阻尼材料在轻质结构振动噪声抑制的高效利用提供科学手段。

约束阻尼结构的拓扑优化大多以模态损耗因子(或模态阻尼比)为优化目标。郭中泽等［1］采用密度法(Pseudo－density Method)及有理逼近材料特性模型(RAMP)，以模态损耗因子最大化为目标，利用优化准则法，获得一定约束条件下阻尼材料的最优分布构型。吕毅宁等［2］采用模态应变能方法计算模态损耗因子灵敏度，对车身地板的阻尼材料进行优化设计。Zheng等［3］以模态阻尼比最大化为目标，采用移动渐近线算法(MMA)对约束阻尼板进行优化，认为移动渐近线算法对约束阻尼圆柱壳优化求解效果较好。Ansari等［4］采用水平集方法对悬臂板上约束阻尼材料进行拓扑优化，获得约束阻尼材料的最佳构型，并实验验证优化结果的正确性。Kim等［5］对比振型法(MSO approach)、应变能分布法(SED method)与拓扑优化算法获得优化结构的模态损耗因子发现，基于有理逼近的材料特性模型(RAMP)及优化准则(OC)拓扑优化方法获得拓扑构型较其它两种方法所得优化结果的模态损耗因子最大值高61.4%。柳承峰等［6］用渐进优化算法对约束阻尼短圆柱壳的约束阻尼结构进行优化，获得约束阻尼材料优化布局，并试验验证优化结果的正确性。

近年来，以结构动力响应为目标的动力学拓扑优化，以其良好的工程实用性及设计针对性成为结构拓扑优化研究热点。Yoon等［7］对模态叠加法、里兹向量法(Ritz Vector)及准静态里兹向量法(Quasi－Static Ritz Vector)3种缩减方法对简谐激励下动力学拓扑优化的适用性进行分析比较;彭细荣等［8］应用结构拓扑优化独立连续映射(ICM)方法，对强迫谐振动下以重量最小为优化目标、位移幅值为约束的板壳结构拓扑优化进行研究;Rong等［9－10］研究了白噪声激励作用下以结构减重为设计目标、指定位置均方响应为约束的拓扑优化设计问题。Shu等［11］以结构某位置频率响应最小为优化目标，以材料使用量为约束条件，采用水平集方法对2D及3D结构进行频率响应优化;李翔等［12］以频带内模态峰值响应的q－范数为优化目标，推导出目标函数灵敏度;增加频率约束可避免迭代过程中密频、重频现象出现，并对桁架结构截面、形状进行优化。刘虎等［13］研究简谐力激励下以结构指定位置稳态阶段位移响应幅值为目标函数、结构体积为约束的拓扑优化设计。上述研究主要集中在结构优化方面，且优化过程中将结构阻尼视为定值，由于结构阻尼变化不大，故此近似带的误差亦不大。但对约束阻尼结构而言，将结构阻尼视为定值则会致较大误差，甚至出现错误结果。

由于约束阻尼技术广泛用于薄壳类轻质结构，如航空发动机零部件及大型空间柔性结构的振动阻尼抑制等，研究以动响应为目标的约束阻尼结构动力学拓扑优化，对推进其设计具有重要意义。本文以指定频带激励下振动响应峰值平方最小化为优化目标，约束阻尼材料用量为约束条件，建立约束阻尼结构的拓扑优化模型，考虑结构模态阻尼比在优化迭代过程中的变化，将模态阻尼比灵敏度引入优化目标灵敏度计算。采用渐进优化算法，通过逐步删除约束阻尼材料中灵敏度最大单元，使保留的单元具有最大减振效果，以达到对约束阻尼材料优化配置目的。

1 结构振动方程求解

简谐激励下结构振动方程为

式中:M，C，K分别为质量、阻尼、刚度矩阵，均为N×N阶实对称矩阵，N为结构自由度数;f(t)=F eiωft为激励力矢量，F为激励力幅值矢量，ωf为激励频率;X分别为结构位移、速度、加速度矢量。

在经典阻尼情况下，方程(1)可转换为

式中:ωi，ζi分别为第 i阶圆频率及模态阻尼比;［φ1，φ2，…，φn］为振型矩阵;yi，qi分别为模态坐标下结构位移、激励力。

据模态叠加法，结构幅频响应表达式为

式中:m为模态截断阶数。

设结构为非密集模态、无重频、小阻尼，当激励频率ωf接近共振频率ωi时，结构第i阶共振频率处响应为

2 约束阻尼结构拓扑优化

2.1 拓扑优化模型

当约束阻尼结构受频带［ωl，ωh］简谐激励，在频带内存在一个或多个共振频率，则共振峰值为X(ωi)。结构动力学拓扑研究中，常以动柔度为优化目标［14－15］，优化整个结构的动力学响应。而实际工程应用中，某些部位的频率响应尤为其重要。本文以激励频段内结构指定位置的共振峰值平方最小化为优化目标，约束阻尼材料用量为约束条件，约束阻尼单元为设计变量建立拓扑优化模型为

式中:pe为设计变量，取0或1;pe=0为删除的结构表面覆盖约束阻尼单元，为避免出现奇异矩阵，宜用极小值;pe=1为结构表面覆盖约束阻尼单元;a为频带内所含共振峰值数量;b为优化目标点数;wi为各峰值叠加系数;V0为约束阻尼材料用量体积;Ve为每个约束阻尼单元体积。

2.2 灵敏度分析

求解拓扑优化模型时采用基于目标函数梯度的迭代方法，需求解目标函数灵敏度表达式。以往以动力响应为优化目标的拓扑优化中常将模态阻尼比定义为定值，未考虑模态阻尼比灵敏度对目标函数灵敏度分析影响，目标函数灵敏度表达式为

考虑对约束阻尼结构优化过程中，约束阻尼结构变化对模态阻尼比影响较大，在已有研究基础上将模态阻尼比灵敏度引入目标函数灵敏度分析中，改进目标函数灵敏度表达式。改进后表达式为

式中:

模态阻尼比与模态损耗因子关系［16］为

当0≤η≤0.3时，模态损耗因子与模态阻尼比的关系可近似为

据应变能法［17］，得第i阶模态损耗因子为

式中:ηv为阻尼材料损耗因子分别为第i阶阻尼层应变能及约束阻尼结构总应变能分别为第i阶j单元基层、阻尼层、约束层应变能。

将式(9)～式(11)代入式(7)可得未考虑模态阻尼比灵敏度的目标函数灵敏度;将式(9)～式(11)、(15)代入式(8)可得考虑模态阻尼比灵敏度的目标函数灵敏度。

为抑制拓扑优化过程中出现棋盘格现象，采用网格独立滤波技术［18］对目标函数灵敏度滤波，即对目标函数灵敏度再分配，使单元灵敏度等于以单元形心为中心的指定半径区域内所有单元灵敏度的加权值。

2.3 渐进优化算法拓扑流程

采用渐进优化算法对拓扑优化模型进行求解，拓扑优化流程见图1。具体优化步骤为:①将约束阻尼材料覆盖于基层结构表面构建全覆盖的约束阻尼结构，并建立有限元模型。将约束阻尼单元(阻尼层单元与其对应的约束层单元)定义为设计变量pe，初始值均为1。②设定约束阻尼材料体积约束量V0、进化率ER及模态截断数等优化相关参数。③对约束阻尼有限元模型进行模态分析，提取约束阻尼单元质量、刚度矩阵、模态阻尼比、模态振型及固有频率等参数。④据目标函数灵敏度公式计算每个约束阻尼单元灵敏度，并用网格独立滤波技术对单元灵敏度滤波。⑤计算下一步迭代的约束材料目标体积，当该体积Vk+1大于设定的体积约束V0时计算式为Vk+1=Vk(1－ER);当Vk+1≤V0时，使Vk+1=V0。据Vk+1确定删除单元门槛值。⑥删除灵敏度值大于删除单元门槛值的约束阻尼单元，将其设计变量pe值由初始值1变为极小值。⑦重复③～⑥，直至满足约束阻尼材料体积约束条件，结束迭代。

图1 拓扑优化流程图Fig.1 Diagram for the topology optimization procedures

3 算例分析

3.1 约束阻尼悬壁板拓扑优化

悬臂约束阻尼板结构见图2，基板为铝板，其上覆盖约束阻尼材料。基板长0.2 m，宽0.1 m，厚0.0008 m，密度2800kg/m3，弹性模量70 GPa，泊松比0.3。阻尼层厚度 0.00005 m，密度 1200kg/m3，弹性模量12 MPa，泊松比 0.495，阻尼材料损耗因子 0.5。约束层厚 0.00013 m，密度 2700kg/m3，弹性模量 70 GPa，泊松比0.3。左端固定，右端自由。

简谐载荷作用于右边界中心即B点，幅值为1 N，激励频带为［10～40］Hz。在激励频段内包含一阶固有频率，取激励点(B点)一阶共振峰值平方最小为优化目标，以约束阻尼材料用量全覆盖的50%为约束条件，分别采用考虑、未考虑模态阻尼比灵敏度目标函数灵敏度计算公式，所得拓扑构型分别见图3、图4。图中浅色为基板，深色为优化的约束阻尼材料拓扑构型;一阶频率、模态阻尼比及优化目标随迭代次数变化分别见图5～图7。优化前后一阶频率、模态阻尼比及优化目标值对比见表1。表1中变化率计算式为

图3 考虑模态阻尼比灵敏度的拓扑构型Fig.3 The topology optimization result with considering the modal damping ratio sensitivity

图4 未考虑模态阻尼比灵敏度的拓扑构型Fig.4 The topology optimization result without considering the modal damping ratio sensitivity

图5 一阶频率迭代历程Fig.5 Iteration history of the firstorder frequency

图6 模态阻尼比迭代历程Fig.6 Iteration history of modal damping ratio

图7 优化目标迭代历程Fig.7 Iteration history of optimization objective

表1 优化前后模态阻尼比与优化目标对比Tab.1 The modal damping ratio and optimization objective before and after optimization

由图5～图7看出，考虑模态阻尼比灵敏度的拓扑优化算法，随约束阻尼材料删除，结构固有频率先增大后(12次迭代后)逐渐减小，模态损耗因子增幅较大，而优化目标逐渐减小，结构模态损耗因子的逐渐增加为优化目标减小的主要因素。未考虑模态阻尼比灵敏度的拓扑优化算法，随约束阻尼材料删除，结构固有频率幅度增大，模态损耗因子逐渐增大，而优化目标逐渐减小，结构固有频率逐渐增大为优化目标减小的主要因素。

在相同激励条件下，以A，B，C点的一阶共振峰值平方及最小为优化目标，以约束阻尼材料用量为全覆盖的50%为约束条件，分别采用考虑、未考虑模态阻尼比灵敏度的目标函数灵敏度计算公式，获得拓扑构型及频率、模态阻尼比随迭代次数变化与以激励点一阶共振峰值平方最小为优化目标的结果相同。优化目标随迭代次数变化见图8，变化趋势同图7。优化前后优化目标分别为0.01 m2，0.0027 m2，0.00065 m2。原因为:对未考虑模态阻尼比灵敏度的优化方法，约束阻尼结构固有频率是使优化目标减小的主要因素;而对考虑模态阻尼比灵敏度优化方法，约束阻尼结构模态阻尼比是使优化目标减小的主要因素，而约束阻尼结构固有频率及模态阻尼比不受响应点位置影响。

图8 优化目标迭代历程Fig.8 Iteration history of optimization objective

由算例看出，本文考虑模态阻尼比灵敏度的拓扑优化算法所得拓扑构型的优化目标值明显低于未考虑模态阻尼比灵敏度时优化目标值。表明在激励频段内仅有单共振峰时该拓扑优化算法的正确性、有效性。

3.2 四边固定约束阻尼板拓扑优化

图9为约束阻尼矩形板，四边固定，长、宽分别为0.6 m、0.4 m，基板为钢板，厚度 0.0015 m，密度 7860kg/m3，弹性模量212 GPa，泊松比0.3。约束阻尼材料厚度及力学参数与上例相同。简谐载荷作用于约束阻尼矩形板中心，幅值1 N，激励频带［0～100］Hz。在激励频带内含一、二阶固有频率，故取激励点处一、二阶共振峰平方的加权最小为优化目标，加权系数可据各阶共振峰值大小及实际应用时关注的共振频率选取。此处选加权系数w1=w2=0.5，约束阻尼材料用量为全覆盖的50%为约束条件，分别采用考虑、未考虑模态阻尼比灵敏度目标函数灵敏度计算公式，所得优化结果见图10、图11，图中浅色为基板，深色为优化的约束阻尼材料拓扑构型。加权频率(w1ω1+w2ω2)、加权模态阻尼比(加权模态阻尼比计算方法)为(w1ζ1+w2ζ2)及优化目标随迭代次数变化分别见图12～图14。优化前后加权频率、加权模态阻尼比及优化目标值对比见表2。表中变化率计算式为

图9 四边固定约束阻尼板Fig.9 The clamped supported constrained layer damping plate

图10 考虑模态阻尼比灵敏度拓扑构型Fig.10 The topology optimization result with considering the modal damping ratio sensitivity

图11 未考虑模态阻尼比灵敏度拓扑构型Fig.11 The topology optimization result without considering the modal damping ratio sensitivity

表2 优化前后模态阻尼比与优化目标对比Tab.2 The modal damping ratio and optimization objective before and after optimization

由图12看出，在优化过程中，随约束阻尼材料的删除，两种拓扑优化算法所得拓扑构型的加权频率均逐渐减小。由图13、图14看出，在频段内具有多共振峰的优化及仅有单共振峰的优化相似。优化过程中，随约束阻尼材料的删除，两种拓扑优化算法所得拓扑构型的加权模态阻尼比均有所增加，而优化目标值均有所减小。此外，本文的考虑模态阻尼比灵敏度优化算法所得拓扑优化构型较未考虑模态阻尼比的优化目标值小。说明本文优化算法对频段内具有多共振峰的优化亦有效。

图12 加权频率迭代历程Fig.12 Iteration history of the weighted frequency

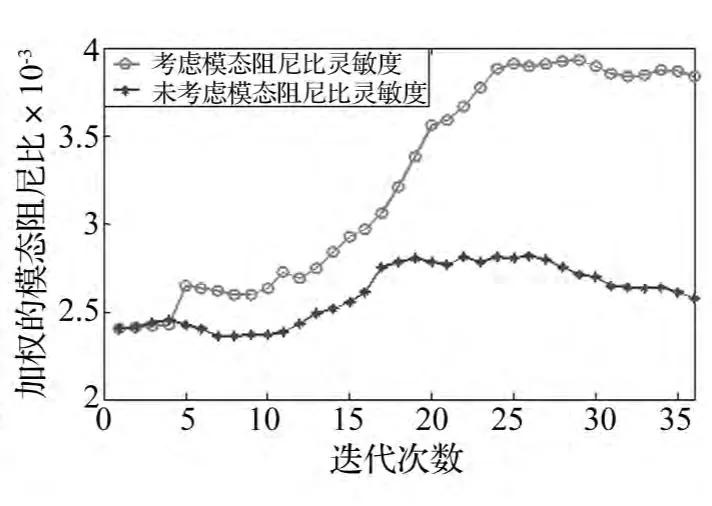
图13 加权模态阻尼比迭代历程Fig.13 Iteration history of the weighted modal damping ratio

图14 优化目标迭代历程Fig.14 Iteration history of optimization objective

4 实验验证

为验证优化算法与灵敏度分析的正确性，对约束阻尼悬壁板以激励点处一阶共振峰平方最小为优化目标的拓扑优化结果进行实验验证。粘贴约束阻尼材料前对铝板待粘贴表面用异丙醇清洗去除油污。粘贴时保证铝板及约束阻尼材料温度不低于15.5℃(50℃最适宜)，从约束阻尼材料一端逐步粘贴整个表面，防止粘贴时起泡影响效果。粘贴后压紧约束阻尼材料，以获得更好粘贴效果。3种约束阻尼悬臂板试件见图15。

图15 实验件Fig.15 The CLD plates using in the tests

用锤击法分别测量全覆盖约束阻尼悬臂板及两种拓扑优化的约束阻尼悬臂板一阶频响函数。用PCB公司086C03型力锤进行激励、基恩士公司LK－H080型激光位移传感器测量悬臂板振动位移响应，激励点、响应点与算例中激励点、响应点位置相同，均在悬臂端中间。信号采集、分析系统为LMS公司数据采集箱及LMS模态分析软件。实验测试见图16，测试结果见图17，3种约束阻尼板一阶频率、模态损耗因子及响应峰值见表3。

图16 实验测试图Fig.16 The experimental setup

图17 实验频响对比Fig.17 The comparison of experimental frequency response

表3 三种约束阻尼板一阶频率、模态阻尼比及响应峰值对比Tab.3 Comparison of the first order frequencies，modal damping ratio and peak response of three CLD plates

5 结论

(1)通过研究指定频段激励下约束阻尼结构的拓扑优化问题，建立以指定频段激励内共振峰值平方最小化为优化目标、约束阻尼材料用量为约束条件的拓扑优化模型。

(2)考虑约束阻尼结构在优化过程中模态阻尼比变化较大，而结构模态阻尼比对共振峰值有较大影响，将模态阻尼比灵敏度添加到目标函数灵敏度分析中，并采用渐进优化算法对约束阻尼板结构进行优化。

(3)利用考虑模态阻尼比灵敏度分析及优化算法，能使约束阻尼结构模态损耗因子增大，优化目标减小，优化效果更好。并通过实验进一步验证该方法的正确性及有效性。

［1］郭中泽，陈裕泽.基于准则法的阻尼结构拓扑优化［J］.宇航学报，2009，30(6):2387－2391.GUO Zhong－ze，CHEN Yu－ze.Topology optimization of the damping structure with optimal criteria［J］.Journal of Astronautics，2009，30(6):2387－2391.

［2］吕毅宁，吕振华，赵波，等.基于应变能分析的附加阻尼结构设计评价和准则优化方法［J］.振动工程学报，2010，23(6):620－624.LÜ Yi－ning，LÜ Zhen－hua，ZHAO Bo，et al.An evaluation and optimization criteria method for structures with damping treatments based on strain energy analysis［J］.Journal of Vibration Engineering，2010，23(6):620－624.

［3］Zheng Ling， Xie Rong－lu， Wang Yi， et al. Topology optimization of constrained layer damping on plates using method of moving asymptote(MMA)approach［J］.Shock and Vibration，2011，18:221 －244.

［4］Ansari M，Khajepour A，Esmailzadeh E，Application of level set method to optimal vibration control of plate structures［J］.Journal of Sound and Vibration，2013，332:687－700.

［5］Kim S Y，Mechefske C K，Kim I Y.Optimal damping layout in a shell structure using topology optimization［J］.Journal of Sound and Vibration，2013，332:2873 －2883.

［6］柳承峰，李以农，郑玲，等.约束层阻尼短圆柱壳拓扑优化分析及实验研究［J］.振动与冲击，2013，32(18):49－53.LIU Cheng－feng，LI Yi－nong，ZHENG Ling，et al.Topology optimization and tests for a short cylindrical shell with constrained layer damping［J］.Journal of Vibration and Shock，2013，32(18):49－53.

［7］Yoon G H.Structural topology optimization for frequency response problem using model reduction schemes［J］.Computer Methods in Applied Mechanics and Engineering，2010，199(25):1744－1763.

［8］彭细荣，隋允康.强迫谐振动下连续体结构拓扑优化［J］.固体力学学报，2008，29(2):157－162.PENG Xi－rong，SUI Yun－kang.Topology optimization of continuum structure with frequency response constraints［J］.Chinese Journal of Solid Mechanics，2008，29(2):157－162.

［9］Rong J H，Xie Y M，Yang X Y，et al.Topology optimization of structures under dynamic response constraints［J］.Journal of Sound and Vibration，2000，234(2):177－189.

［10］张桥，张卫红，朱继宏.动力响应约束下的结构拓扑优化设计［J］.机械工程学报，2010，46(15):45－51.ZHANG Qiao，ZHANG Wei－hong，ZHU Ji－hong.Topology optimization of structures under dynamic response constraints［J］.Journal of Mechanical Engineering，2010，46(15):45－51.

［11］Shu L，Wang M Y，Fang Z，et al.Level set based structural topology optimization for minimizing frequency response［J］.Journal of Sound and Vibration，2011，330(24):5820－5834.

［12］李翔，王皓，陈力奋.结构频带激励下的整体动响应优化［J］.振动与冲击，2012，31(9):113－117.LI Xiang，WANG Hao，CHEN Li－fen.Structural frequency response optimization under bandwidth excitation［J］.Journal of Vibration and Shock，2012，31(9):113－117.

［13］刘虎，张卫红，朱继宏.简谐力激励下结构拓扑优化与频率影响分析［J］.力学学报，2013，45(4):588－597.LIU Hu， ZHANG Wei－hong， ZHU Ji－hong. Structural topology optimization and frequency influence analysis under harmonic force excitations ［J］. Chinese Journal of Theoretical and Applied Mechanics，2013，45(4):588－597.

［14］Ma Z D，Kikuchi N，Hagiwara I.Structural topology and shape optimization for a frequency response problem［J］.Computational Mechanics，1993，13(3):157－174.

［15］Jog C S.Topology design of structures subjected to periodic loading［J］.Journal of Sound and Vibration，2002，253(3):687－709.

［16］Graesser E J，Wong C R.The relationship of traditional damping measures for materials with high damping capacity:a review［M］.Mechanics and Mechanisms of Material Damping，1992:316－343.

［17］Johnson C D，Kienholz D A.Finite element prediction of damping in structures with constrained viscoelastic layers［J］.AIAA Journal，1982，20(9):1284 －1290.

［18］Sigmund O，Petersson J.Numerical instabilities in topology optimization:a survey on procedures dealing with checkerboards，mesh－dependencies and local minima ［J］.Structural Optimization，1998，16(1):68－75.