切削式吸能热力耦合研究
刘国伟,夏 茜,王千叶,董茹玲
(1.中南大学 交通运输工程学院 轨道交通安全教育部重点实验室,长沙 410075;2.中国铁建重工集团研究设计总院,长沙 410100;3.中交第二公路勘察设计研究院有限公司,武汉 430056)
随轨道交通的迅速发展,列车撞击事故频繁发生。吸能装置可在碰撞瞬间吸收能量、缓和冲击,为列车被动防护的主要措施[1]。轨道车辆专用吸能装置主要通过金属材料塑性变形、压溃过程及综合过程等3种吸能方式[2-4]。金属切削过程作为典型的金属破碎过程,会在短时间内消耗大量能量。若使刀具承受的外来撞击能量通过驱动刀具切削工件消耗掉,则此过程即为切削式吸能过程。在此过程中被切削材料发生塑性变形直至撕裂;同时刀具与工件被切削面发生摩擦,通过金属材料的塑性变形、撕裂等综合作用吸收能量[5-6]。因此,理论上讲,切削式吸能为较理想的能量吸收方式。
金属切削加工及切削式吸能均通过金属切削过程实现,但对其研究目的存在较大差异。前者主要针对刀具、工件、加工过程及设备,以获得理想的工件形状、尺寸及表面质量的研究。而后者则对切削后工件形状、表面质量无要求,研究重点集中于能量消耗过程,即切削力、切削速度及能量消耗的变化规律及影响该规律因素。切削加工过程能量持续输入基本不变,刀具在设定的进给速度下切削工件。切削式吸能过程仅给定初始撞击能量输入,无其它能量输入;随切削吸能过程进行,撞击能量耗散,切削速度逐渐减小。切削加工一般要求切削热尽量减小,而切削式吸能过程可充分利用切削热消耗撞击能量。
目前,虽对金属切削加工研究已较全面[7-10],但对切削式吸能研究却刚开始。文献[5]对切削式吸能过程进行三维仿真表明,切削式吸能能力强,较现有吸能装置相比撞击力峰值小。文献[6]对切削式吸能装置进行设计及优化。雷成等[11-13]对金属切削式吸能过程仿真研究并设计出车辆端部专用吸能装置,结果表明切削式吸能为理想的吸能模式,吸能装置冲程效率及压缩力效率均高于现有吸能装置。
以上研究均未考虑热效应,而实际切削过程会产生热量,切削热会影响吸能过程,亦会耗散一定碰撞能量。因此,全面研究切削式吸能过程,除考虑材料变形及撕裂过程外,尚须研究碰撞过程中热效应影响。因此,对切削式吸能过程的热力耦合分析十分必要。
本文选择合适的材料模型、接触方式、单元尺寸等建立切削式吸能过程的热力耦合求解模型。利用非线性动态模拟软件LS-DYNA对切削式吸能过程进行数值模拟,研究切削热对切削吸能过程影响。在热力耦合前提下,分析切削速度、切削截面参数及刀具参数对切削式吸能影响规律。所得结果对设计轨道车辆切削式吸能装置有重要参考价值。
1 切削式吸能热力耦合数值模拟方法
由于切削式吸能过程为极复杂的非线性动态响应过程,而计算机仿真可较合理模拟结构碰撞切削过程,本文对基本控制方程及热力耦合热传导控制方程进行简述[14-17]。
1.1 基本控制方程
结构碰撞中虽变形剧烈,但基本过程仍由运动、变形、接触及摩擦等物理过程构成,满足质量守恒、能量守恒定律及运动方程等基本物理规律。结构碰撞过程基本控制方程为

式中:ρ0,ρ分别为初始时刻、任意时刻材料密度;为形变梯度行列式;wint为单位质量内能;D为结构变形率;s为热源;q为热流量;σij为柯西应力;ρm为瞬时质量密度;fi为体积力密度为加速度。
碰撞过程中位移边界条件为

面力边界条件为

式中:Ki(t)为结构碰撞中位移边界给定位移函数;nj为结构面力边界外法线方向余弦;Ti(t)为结构面力载荷。
1.2 热传导控制方程
切削吸能过程的切削热主要源于被切削区域材料的塑性变形及刀屑间摩擦。设材料塑性功转换为内热源,且材料导热各向同性,将切削式吸能过程在某Ω域内的三维导热微分方程表述为
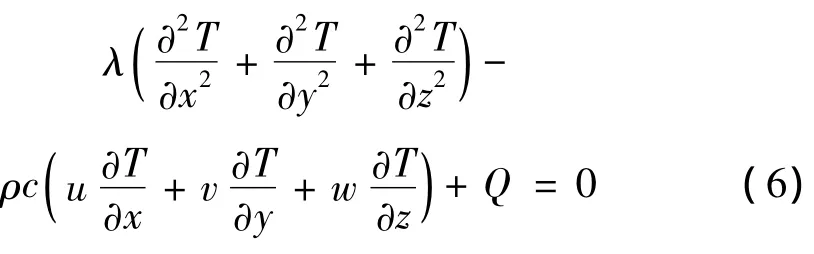
热边界应满足

式中:T为切削温度场中某点温度;λ为热容值;Q为材料塑性变形内热源;Γ为Ω区域全部边界;Γ1,Γ2,Γ3分别为室温、传导及对流边界。
本文对切削式吸能过程热效应假设为:① 初始撞击动能通过切削力做功而耗散,一部分由切屑的形成及飞溅实现,另部分由热效应实现。② 忽略热对流及热辐射影响,只考虑刀具与工件间热传导及散热。③工件材料力学特性及导热均各向同性。④ 忽略因温升造成的金相变化及其它化学变化。
切削过程中工件材料因温升会形成初应变ε0,热力耦合计算时,总应变包括弹性应变与初应变,即
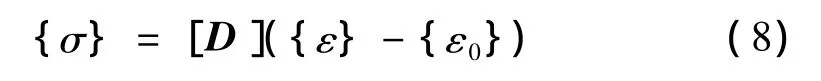
式中:[D]为弹性矩阵;{σ}为热应力。
2 切削式吸能热力耦合求解模型
本文利用LS-DYNA软件建立切削式吸能结构的有限元模型,并定义相关热力耦合控制参数。
2.1 切削式吸能模型几何参数
与传统切削加工不同,切削式吸能不考虑材料表面加工质量,撞击方向即切削方向,且刀具只需一个主切削刃。给定撞击初始条件及金属材料时,其主要切削参数包括切削深度、切削宽度、刀具前角、刀具后角(不考虑刀尖圆弧半径影响)。切削参数见表1。

表1 切削参数Tab.1 Cutting parameters
为避免切削力剧烈波动,取刀具前角>0°,可使整个切削式吸能过程平稳。初始撞击能量取20 kJ。撞击初始速度取城轨车辆允许最高撞击速度10 m/s。
2.2 刀具与工件材料选取
由轨道车辆专用吸能装置角度考虑,工件材料选硬度合适、低成本的Q235钢。由于切削式吸能过程初始撞击速度较大,刀具材料须具备一定韧性且耐高温、耐冲击;刀具切削方向单一,形状简单,选硬质合金YG8作为切削式吸能刀具材料。刀具与工件材料参数见表2。

表2 刀具与工件材料参数Tab.2 Material parameters of cutting tool and workpiece
2.3 数值计算模型相关参数
2.3.1 单元选取及网格划分
采用适合三维结构实体的3DSolid164单元,该单元支持Johnson-Cook塑性材料及所有非线性特征的动态分析。
由于切削式吸能过程中在局部区域内材料产生高温及大变形,在数值模拟中会形成网格畸变或退化,从而影响计算的收敛性及准确度。因此,综合考虑计算效率及精度,细分切削区域及附近网格,远离切削区域网格粗化处理。考虑网格单元有序性,全部采用映射网格划分,见图1(单位mm)。

图1 模型网格划分Fig.1 Mesh model
2.3.2 材料模型
切削式吸能过程存在工件塑性变形、刀屑摩擦、刀具与工件摩擦及温升、材料软化及刀具与工件间热传递等,因此需选择能反映材料的力学特性及材料温升软化效应模型。
本文选Johnson-Cook材料模型,其本构关系模型采用Mises屈服面,用不同强化准则并考虑应变率与温度影响,可较准确模拟金属材料大变形,具体构成方程式为


表3 工件Johnson-Cook材料模型参数Tab.3 Johnson-Cook material parameters of workpiece
Johnson-Cook本构方程中,为模拟切屑与工件分离情况,用方程式表示材料达到破坏时所需应变,即

式中:εf为允许破坏应变值为累积破坏应变值;D1,D2,D3,D4,D5为失效参数常数,可通过切削试验测得。失效参数取值[19]见表4。当累积破坏应变值D=1时,单元发生失效。

表4 模型失效准则参数取值Tab.4 model failure criterion parameters
计算前需对刀具、工件赋予各向同性热材料模型,对应关键字为*MAT_THERMAL_ISOTROPIC,在其中定义材料的热密度、比热容及导热率等参数(表2)。
2.3.3 接触处理
刀具与工件间采用面面侵蚀接触,该接触可设定动、静摩擦系数及是否侵蚀内部节点,而刀屑接触、切屑与切屑接触采用自动单面接触,动、静摩擦系数分别设为0.15及0.1。在刀具与工件间设定面-面热接触,模拟热传导过程。
2.3.4 约束载荷
结合切削式吸能过程实际情况,对模型设置边界条件。刀具Y,Z方向位移自由度为0;工件底面全约束(图1)。
2.3.5 切屑分离准则
常用切屑分离准则主要有几何分离及物理分离。前者据刀尖与刀尖前单元节点距离变化判断分离与否;后者则据应力、应变及应变能等是否达到临界值判断。本文采用物理分离准则,节点应力值达到失效应力时单元失效,切屑即与工件分离。
3 切削式吸能热力耦合计算结果分析
据所设参数,利用LS-DYNA进行非线性动力学分析,获得数值模拟结果。
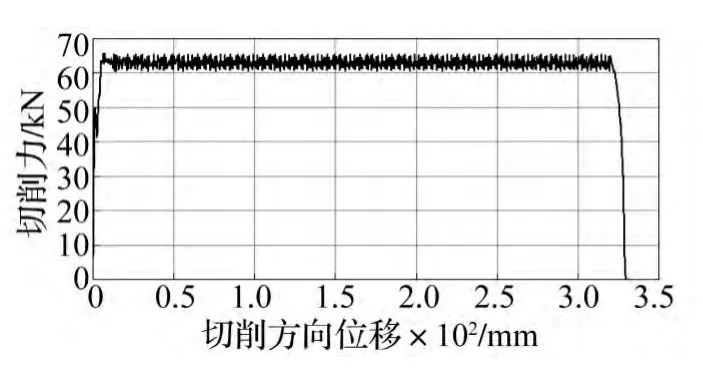
图2 总切削力曲线Fig.2 Curve of cutting force
3.1 切削式吸能过程切削力变化
切削式吸能过程总切削力曲线见图2。由图2看出,刀具刚切入工件时,为使工件产生塑性变形,需较大的力作用,故切削力急剧增大,形成小峰值。工件切开后由于裂纹扩展使撕裂更容易,切削力有所下降;随行程增加切屑堆积阻尼加大,切削力逐渐增大,直至达到某个稳定值。在稳定区段,切削力仍在小范围内波动。原因为:刀具切削过程有轻微震动、划分的网格单元不断失效及采样频率影响。切削完成后,切削力迅速下降至0。
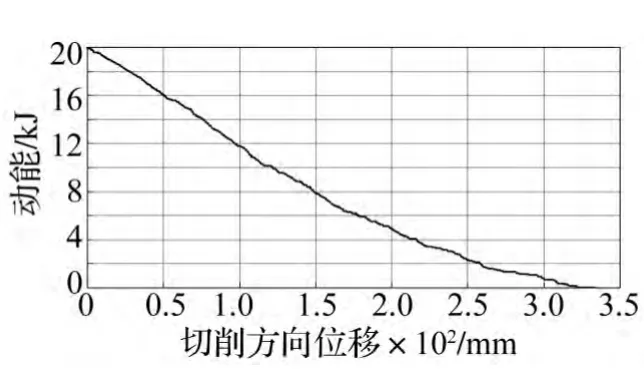
图3 刀具动能变化曲线Fig.3 Curve of kinetic energy in cutting process of metal

图4 工件、刀具最高温度Fig.4 Highest temperature of workpiece and cutting tool
较文献[5-6]切削力曲线,本文曲线未出现较大初始峰值。因其为增加吸能量均用0°刀具前角,导致初始撞击力急剧增加,形成较大初始峰值。就切削式吸能实际用途而言,应尽量避免切削力的剧烈波动。本文将刀具前角设为15°,使整个切削吸能过程相对平稳,避免较大初始切削力峰值。
3.2 切削式吸能过程的动能变化
切削式吸能过程刀具动能变化见图3。由图3看出,切削过程能量不断消耗,刀具初始动能由最初20 kJ减少至0 kJ,主要通过切削力做功实现,其中包括工件塑性变形、切屑消耗的能量及热效应耗散的能量,整条能量变化曲线细微波动均由切削力波动所致。
3.3 切削式吸能过程热效应
工件与刀具在整个切削吸能过程中最高温度变化曲线见图4。由图4看出,切削开始后刀具与工件温度急剧上升,并随刀具行程增加,刀具、工件温度随之增高,但幅度逐渐减小,进入稳态后,基本保持在一稳定值。因随初始动能不断耗散,切削速度不断减小,单位时间内产生的热量随之减少,加之散热作用,使刀具、工件最高温度基本不变化。刀具最高温度远低于工件,主要因刀具传热系数较小,不易传热。
切削过程不同时刻温度分布云图见图5。由图5看出,温升范围随切削过程进行不断扩大,其分布区域主要集中在接触面与刀尖有一定距离处,刀具温度基本无变化。

图5 不同时刻刀具与工件温度分布Fig.5 Temperature distribution of cutting tool and workpiece in different time
切削过程中刀具与工件温度分布见图6。切屑与刀具接触处由于摩擦作用温度最高,出现在工件上为598.33℃,主要分布在刀-屑接触面距刀尖有一定距离处,并逐渐向外递减。工件与刀具最高温度均未超过材料熔点,因此在切削吸能过程中不会发生熔融现象。整个切削吸能过程共吸收能量20 kJ,其中热耗散能所占比例约21%,见图7。可见切削热对整个吸能过程产生非常重要影响。
4 切削式吸能力学与热学性能影响因素分析
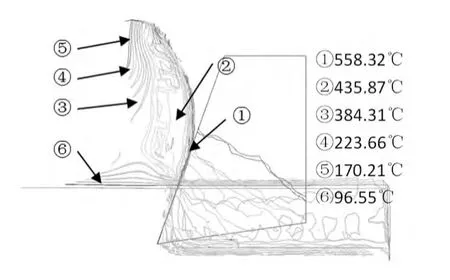
图6 切削过程中刀具与工件温度分布Fig.6 Temperature distribution of cutting tool and workpiece in the process of cutting
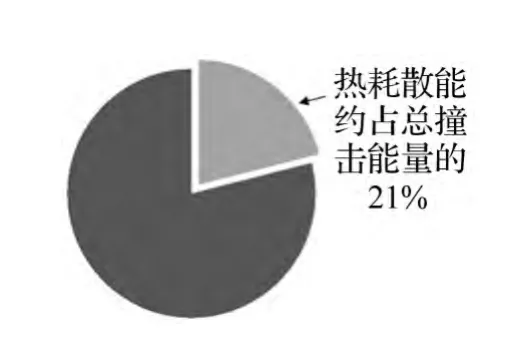
图7 能量分配情况Fig.7 The energy distribution
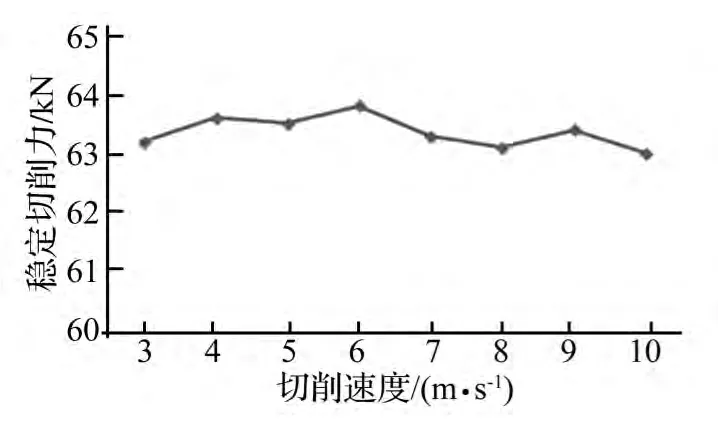
图8 定初始动能时稳定切削力随撞击速度变化Fig.8 Steady cutting force versus cutting velocity under constant initial kinetic energy

图9 定初始动能时最高温度及热耗散能量百分比随撞击速度变化Fig.9 The maximum temperature and percentage of thermal dissipation energy versus cutting velocity under constant initial kinetic energy

图10 变初始动能时稳定切削力随撞击速度变化图Fig.10 Steady cutting force versus cutting velocity under various initial kinetic energy
切削式吸能过程会受刀具参数、切削条件等多因素影响,若将切削式吸能结构用于轨道交通领域,须对该过程深入探讨,在热力耦合前提下,分析各种因素对切削式吸能特性影响。
4.1 撞击速度对切削式吸能影响
4.1.1 定初始动能
撞击速度与撞击能量有关,保持初始动能20 kJ不变,改变撞击速度与撞击质量组合,所得稳定切削力随速度变化曲线见图8。稳定切削力始终保持在63~64 kN之间,最高温度及热耗散百分比随速度变化曲线见图9。
计算结果显示,初始撞击能量保持一定时,在不改变其它切削参数前提下,撞击质量、撞击速度组合变化对切削力影响很小。最高温度与热耗散能量比例随切削速度增加而增大,但二者增加幅度均呈不断减小趋势。
4.1.2 变初始动能
保持一定撞击质量、改变撞击速度,获得变初始动能时切削式吸能的稳定切削力随速度变化曲线见图10,最高温度及热耗散能量所占比例随速度变化曲线见图11。计算结果表明,随撞击速度增加切削力缓慢减小。此因提高切削速度后材料间摩擦系数随之减小,剪切角增大,导致单位面积所需切削力减小;而随切削速度提高温度升高,使材料变软更易切削;但在该切削参数下,速度影响不明显,基本可忽略。由图11看出,变初始动能时,热耗散能量及所占比例随切削速度提高而增加。
据以上分析结果,在切削截面、刀具参数不变前提下,切削力对初始撞击条件变化基本不敏感,而热效应则随撞击速度增加而增加。
4.2 切削截面参数对切削式吸能影响
4.2.1 切削深度
切削宽度保持30 mm不变,结合机加工常用工件切削深度选择范围,切削深度从1~5 mm计算所得稳定切削力、切削位移随切削深度变化见图12,最高温度、热耗散百分比随切削深度变化见图13。由图12看出,切削力随切削深度增加而增加,切削行程则随切削深度增加而减小。此因切削层越厚,发生塑性变形所需能量越多,初始能量耗散越多,切削过程中阻尼越大。由图13看出,随切削深度增加,最高温度、热耗散能量及所占比例均呈小幅度增大。
4.2.2 切削宽度
切削深度保持3 mm不变,切削宽度从10~50 mm计算所得切削力与切削位移变化见图14,最高温度与热耗散百分比变化见图15。由图14看出,切削力随切削宽度增加而增大,切削位移则随切削宽度增加而减小。此因工件被切削的区域越宽,发生塑性变形的单元数量越多,所需能量越多,切削过程中由切屑产生的阻尼越大。由图15看出,随切削宽度增加,最高温度呈小幅度增大,热耗散能量及所占比例无明显变化。

图11 变初始动能时最高温度及热耗散能量百分比随速度变化曲线Fig.11 The maximum temperature and percentage of thermal dissipation energy versus cutting velocity under various initial kinetic energy

图12 不同切削深度稳定切削力与切削位移变化Fig.12 Steady cutting force and cutting stroke versus cutting depth

图13 不同切削深度最高温度与热耗散百分比变化曲线Fig.13 The maximum temperature and percentage of thermal dissipation energy versus cutting depth

图14 不同切削宽度稳定切削力与吸能量变化Fig.14 Steady cutting force andenergy absorption versus cuttingwidth

图15 不同切削宽度的最高温度和热耗散百分比变化曲线Fig.15 The maximum temperature and percentage of thermal dissipation energy versus cutting width
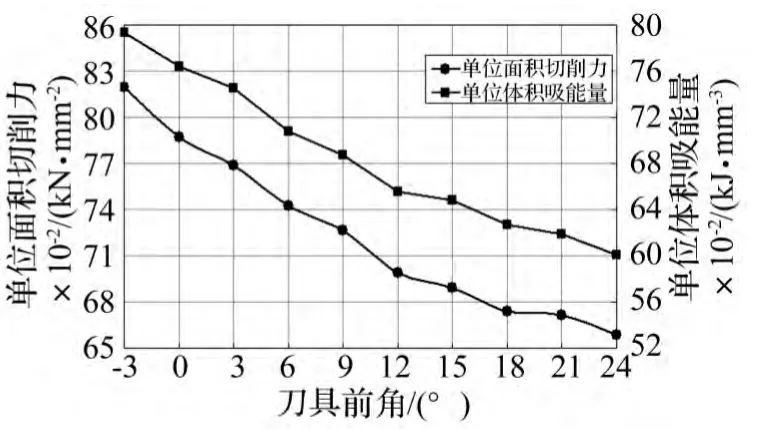
图16 不同前角单位面积切削力与单位体积吸能量变化Fig.16 Cutting force per unit area and energy absorption per unit volume with differenttool rake angle
4.3 刀具参数对切削式吸能影响
4.3.1 刀具前角
后角保持8°不变,前角由 -3°等差递增至24°共10组数据,计算所得单位面积切削力与单位体积吸能量变化见图16。由图16看出,单位面积切削力与单位体积吸能量随刀具前角增大而减小,呈非线性变化。前角小于3°时切削力稳定性受到一定影响,波动较剧烈,不利于实际工程应用。
热耗散能所占比重随刀具前角变化见图17。由图17看出,增大刀具前角热耗散能比重随之减小,此因前角增大会导致工件被切削面塑性变形与刀屑间摩擦减小,加之散热空间变大,故切削温度与热耗散能比重均会降低。
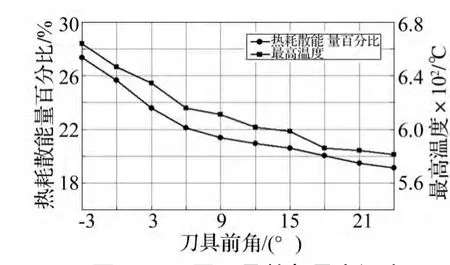
图17 不同刀具前角最高温度及热耗散能量百分比变化Fig.17 The maximum temperature and percentage of thermal dissipation energy with different tool rake angle
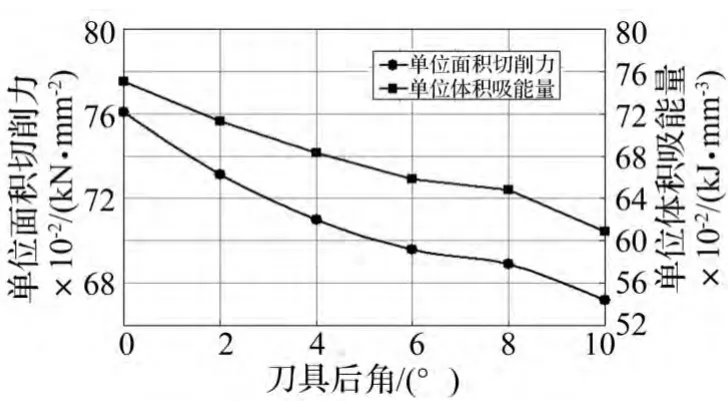
图18 不同后角单位面积切削力与单位体积吸能量变化Fig.18 Cutting force per unit area and energy absorption per unit volume with different tool base clearance
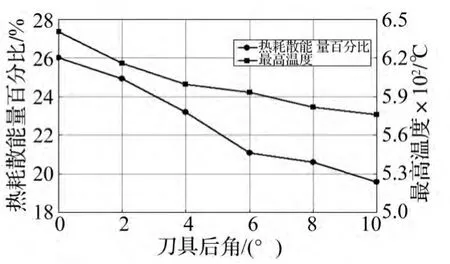
图19 不同后角最高温度、热耗散能量百分比变化Fig.19 The maximum temperature and percentage of thermal dissipation energy with differenttool base clearance
4.3.2 刀具后角
前角保持15°不变,后角由0°等差递增至10°计算所得单位面积切削力与单位体积吸能量变化见图18,热耗散能所占比重随刀具后角变化见图19。由二图看出,其它切削参数不变时单位面积切削力与单位体积吸能量随刀具后角增大而减小;热耗散能比重随刀具后角增大而减小。此因后角增大会减小切削后表面与刀具间摩擦,增大散热空间,故切削温度、热耗散能比重均会降低。
5 结论
(1)切削式吸能过程中撞击力起伏较小,未出现剧烈波动,不会有较大初始峰值。若用于轨道车辆专用吸能装置将更符合人体承受力要求,为相对稳定的新型吸能方式。
(2)切削式吸能过程中工件、刀具最高温度均未超过材料熔点,不会发生熔融现象;但热耗散形式吸收的撞击能量所占比重达到21%,材料塑性变形及撕裂等吸收的撞击能量占79%。故切削热对整个吸能过程影响不可忽略,数值模拟研究中需考虑切削热影响。
(3)切削截面、刀具参数不变前提下,无论初始撞击能量是否恒定,切削速度对切削力产生的影响较小,而热效应则随撞击速度增加而增加;切削截面尺寸直接影响切削式吸能过程,切削力随切削深度及宽度增加而增大,但对热耗散能量影响较小;单位面积切削力与单位体积吸能量随刀具前角或后角增大而呈曲线减小,热耗散能所占比重随刀具前角或后角增大而曲线减小。
[1]张曙.大力发展城市轨道交通[J].湖南交通科技,2000,26(4):70-72.ZHANG Shu.Developing urban rail transit[J].Journal of Hunan Traffic Science and Technology,2000,26(4):70-72.
[2]孙彦彬,张伟,陈秉智,等.折叠式压溃管的吸能仿真[J].大连交通大学学报,2008,29(5):105 -108.SUN Yan-bin, ZHANG Wei, CHEN Bing-zhi, et al.Simulation of folding crushing tube's energy-absorbing[J].Journal of Dalian Jiaotong University,2008,29(5):105-108.
[3]贾宇.机车车辆耐撞结构设计与碰撞仿真研究[D].成都:西南交通大学,2005.
[4]于学辉.铁路客车冲击试验研究[J].国外铁道车辆,1999,36(4):31-32.YU Xue-hui.Research on impacting test of railway passenger car[J].Journal of Foreign Railway Vehicle,1999,36(4):31-32.
[5]常宁.切削式吸能过程仿真研究[D].长沙:中南大学,2009.
[6]汤礼鹏.城轨车辆切削式专用吸能装置研究[D].长沙:中南大学,2010.
[7]Merchant M E.Mechanics of the metal cutting process[J].Appl.Physics,1945,16:267 -275.
[8]Lee L E,Shaffer D W.The theory of plastic applied to a problem of machining[J].Trans.ASME J.Appl.Mech.,1951,118:405-413.
[9]Usui E,Maekawa K,Shirakashi T.Simulation analysis of built-up edge formation in machining of low carbon steel[J].Bull.Japan Soc.Prec.Eng.,1981,15(4):237 -242.
[10]郭培燕,王素玉,冯桢,等.高速切削加工表面残余应力的产生和控制[J].工具技术,2007,41(3):46-47.GUO Pei-yan,WANG Su-yu,FENG Zhen,et al.Generate and control of high-speed machining surface residual stress[J].Journal of Tool Technology,2007,41(3):46-47.
[11]雷成,肖守讷,罗世辉.轨道车辆新型车端专用吸能装置[J].西南交通大学学报,2013,48(4):738 -744.LEI Cheng, XIAO Shou-na, LUO Shi-hui. New special energy-absorbing component at vehicle end of rail vehicles[J].Journal of Southwest Jiaotong University,2013,48(4):738-744.
[12]雷成,肖守讷,罗世辉.轨道车辆切削式吸能装置吸能特性研究[J].中国机械工程,2013,24(2):263 -267.LEI Chen,XIAO Shou-na,LUO Shi-hui.Research on energy absorption characteristic of rail vehicle energy-absorbing component in cutting way[J].Journal of China Mechanical Engineering,2013,24(2):263 -267.
[13]雷成,肖守讷,罗世辉.金属切削式吸能过程的仿真研究[J].煤矿机械,2013,34(5):159 -160.LEI Cheng, XIAO Shou-na, LUO Shi-hui. Simulation researching on energy absorption process in metal-cutting way[J].Coal Mine Machinery,2013,34(5):159 -160.
[14]Singace A,Elsobky H.On the eccentricity factor in the progressive crushing of tubes[J].Solids and Structures,1995,32(1):3589-3602.
[15]Sridharan S S,Kasagi A.Dynamic buckling of composite shells[J].Computers and Structures,1996,59(1):43-53.
[16]Bathe K J.Finiteelement procedures[M].New Jersey:Prentice Hall,Englewood Cliffs,1996:485 -640.
[17]Schauer D A,Hoover C G,Kay G J.Crashworthiness simulations with DYNA3D[J].Transportation Research Record,1996,29(2):124-129.
[18]牟金磊,朱锡,黄晓明,等.水下爆炸气泡载荷在加筋板塑性变形中的作用[J].振动与冲击,2010,29(5):74-77.MU Jin-lei,ZHU Xi,HUANG Xiao-ming,et al.Explosion load of underwater gas bubbles in the role of stiffened plate plastic deformation[J].Journal of Vibration and Shock,2010,29(5):74 -77.
[19]卢文浩,鲍荣浩.动态冲击下能量吸收结构的惯性敏感性的数值模拟分析[J].振动与冲击,2004,23(3):67-69.LU Wen-hao,BAO Rong-hao.The numerical simulation of energy absorption structure's inertial sensitivity under dynamic impact energy[J].Journal of Vibration and Shock,2004,23(3):67-69.

