Hilbert空间中均衡问题与渐近非扩张半群的迭代算法的强收敛性

来希雪， 黄建华

(福州大学数学与计算机科学学院， 福建 福州 350116)

Hilbert空间中均衡问题与渐近非扩张半群的迭代算法的强收敛性

来希雪， 黄建华

(福州大学数学与计算机科学学院， 福建 福州 350116)

针对均衡问题和渐近非扩张算子半群的公共元问题, 提出一个新的迭代算法, 在合适的条件下, 证明了由此迭代算法生成的序列的强收敛性定理.

Mann迭代格式; 渐近非扩张半群; 均衡问题; 公共不动点

0 引言

Φ(x,y)≥0 (∀y∈C)

本文用EP(Φ)表示(1)式的解集.众所周知, 问题(1)有着广泛的应用, 很多问题都可以归结为均衡问题.例如, 变分包含问题, 变分不等式的不动点问题, 最优化问题等.

假设二元函数Φ:C×C→R满足下列条件:

(A1)Φ(x,x)=0, ∀x∈C;

(A2)Φ是单调的, 即Φ(x,y)+Φ(y,x)≤0, ∀x,y∈C;

(A4) 对每个x∈C, 函数y|→Φ(x,y)是凸的和下半连续的.

称Γ={T(t):C→C;t≥0}为C的Lipschitzian半群[1], 如果满足如下条件:

1)T(0)x=x, ∀x∈C;

2)T(s+t)x=T(s)·T(t)x, ∀s,t≥0, ∀x∈C;

3) 存在有界可测泛函L:(0, ∞)→[0, ∞), 使得

4) 对每一个x∈C, 映射t|→T(t)x在[0, ∞)上都是连续的.

Kima和Xu[2]针对渐近非扩张映射及渐近非扩张半群的不动点的公共元， 提出了如下修正的Mann迭代算法:

Tada和Takahash[3]针对均衡问题和非扩张映射的不动点的公共元, 提出了如下的混合迭代算法:

受到以上结论的鼓舞和启发, 本文针对均衡问题和渐近非扩张半群的不动点的公共元; 提出如下的算法:

{tn}是一个正的发散实序列; 在适当的条件下, 证明了由算法(2)生成的序列强收敛于均衡问题和渐近非扩张半群的不动点的公共元.本文去掉文献[2]的定理3.3中C的有界性条件.此外, 本研究的结果较文献[2-3]具有更广泛的意义.

1 预备知识

下面追述一些概念和众所周知的结论:

若{xn}是H中弱收敛于z的序列, 则

∀

引理1[4-5]设C为H的非空闭凸子集, 二元函数Φ:C×C→R满足条件(A1)～(A4).设λ>0和x∈H, 则存在u∈C, 使得

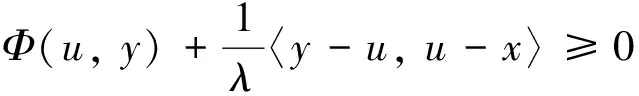
1)Tλ是单值的;

2)Tλ是稳定非扩张的(firmly nonexpansive), 即

3)F(Tλ)=EP(Φ);

4) EP(Φ)是非空闭凸的.

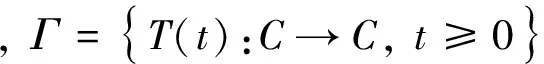
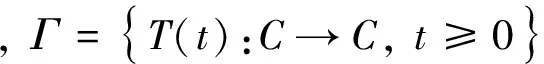
2 主要结论

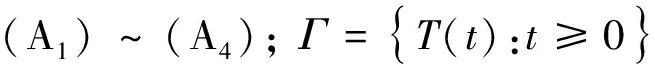
证明 以下分五步完成定理的证明.

第一步 证明F(Γ)∩EP(Φ)⊂Cn∩Qn, ∀n≥0. 显然Qn是闭凸集. 由引理3可得,Cn是闭凸集. 下面利用数学归纳法证F(Γ)∩EP(Φ)⊂Cn. 当n=0时, 明显F(Γ)∩EP(Φ)⊂C0=C. 假设当n≥1时,F(Γ)∩EP(Φ)⊂Cn. 那么对任意F(Γ)∩EP(Φ)的元素p, 有

∀

从而

因此p∈Cn+1, ∀n≥0, 即F(Γ)∩EP(Φ)⊂Cn+1.

下面证明F(Γ)∩EP(Φ)⊂Qn, ∀n≥0. 当n=0时, 显然F(Γ)∩EP(Φ)⊂Q0. 假设当n≥1时,F(Γ)∩EP(Φ)⊂Qn, 即对∀p∈F(Γ)∩EP(Φ), 都有〈xn-p,x0-xn〉≥0. 由xn+1=PCn∩Qn(x0)得〈xn+1-p,x0-xn+1〉≥0(∀p∈Cn∩Qn), 因此p∈Qn+1, 于是F(Γ)∩EP(Φ)⊂Qn+1.

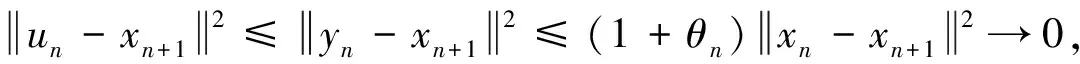
且

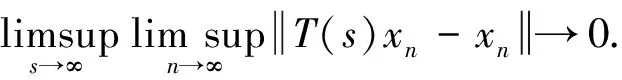
对任意的0≤s<∞, 都有

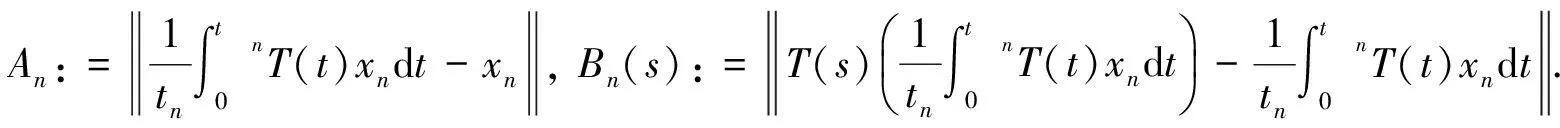
因此

根据(A2)可得，

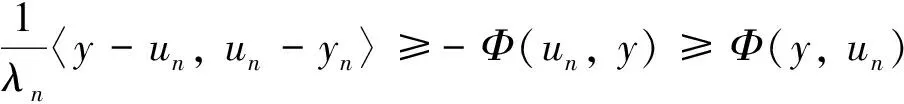
令n→∞, 不等式两边同时取极限, 结合(9)式和(A4)可得∀y∈C,Φ(y,p*)≤0.

设0

因此，Φ(yt1,y)≥0. 令t→0, 根据(A3)可得,Φ(p*,y)≥0, ∀y∈C. 所以p*∈EP(Φ).

[1]XuHongkun.Strongasymptoticbehaviorofalmost-orbitsofnonlinearsemigroups[J].NonlinearAnal, 2001, 46(1): 135-151.

[2]KimaTH,XuHongkun.StrongconvergenceofmodifiedManniterationsforasymptoticallynonexpansivemappingsandsemigroups[J].NonlinearAnalysis, 2006, 64(5): 1 140-1 152.

[3]TadaA,TakahashiW.Weakandstrongconvergencetheoremsforanonexpansivemappingsandanequilibriumproblem[J].OptimTheoryAppl, 2007, 133(3): 359-370.

[4]CombettesPL,HirstoagaSA.EquilibriumprogramminginHilbertspaces[J].JournalofNonlinearandConvexAnalysis， 2005, 6(1): 117-136.

[5]TakahashiS,TakahashiW.ViscosityapproximationmethodsforequilibriumproblemsandfixedpointproblemsinHilbertspaces[J].MathAnalAppl， 2007, 331(1): 506-515.

[6]MartinesYC,XuHongkun.StrongconvergenceofCQmethodforfixedpointiterationprocess[J].NonlinearAnalysis:Theory,Methods&Applications， 2006, 64(11): 2 400-2 411.

[7]TanKK,XuHongkun.ThenonlinearergodictheoremforasymptoticallynonexpansivemappingsinBanachspaces[J].ProcAmMathSoc, 1992, 114(2): 399-404.

(责任编辑： 林晓)

Strong convergence of an iterative method for equilibrium problems and asymptotically nonexpansive semigroups in Hilbert space

LAI Xixue， HUANG Jianhua

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

We propose an iterative scheme for finding a common element of the solutions of an equilibrium problem and the fixed points of asymptotically nonexpansive semigroups. Under some appropriate conditions, we establish a strong convergence theorem of the sequence generated by our proposed scheme.

Mann iterative scheme; asymptotically nonexpansive semigroups; equilibrium problem; common fixed point

10.7631/issn.1000-2243.2015.04.0445

1000-2243(2015)04-0445-05

2013-04-12

黄建华(1957-), 教授， 主要从事非线性泛函分析研究， 412221616@qq.com

福建省自然科学基金资助项目(2012J01005)

O177.91

A