计及节点相关性的含间歇分布式电源配电网概率潮流

刘洪，葛少云，张鑫，马康，刘军

(1．智能电网教育部重点实验室，天津大学，天津300072; 2．国网天津市电力公司电力科学研究院，天津300384;3．中国电力科学研究院，北京100192)

计及节点相关性的含间歇分布式电源配电网概率潮流

刘洪1，葛少云1，张鑫2，马康3，刘军3

(1．智能电网教育部重点实验室，天津大学，天津300072; 2．国网天津市电力公司电力科学研究院，天津300384;3．中国电力科学研究院，北京100192)

概率潮流计算是分析含间歇式分布式电源配电网运行状态的重要工具。配电网中各节点负荷特性以及气候条件等多个变量均具有较强的相关性，为此提出了节点间注入功率相关性的计算方法，并通过Cholesky分解对节点间注入功率解耦，形成了适用于有源配电网的计及节点相关性的概率潮流算法。通过对改造的部分IEEE 33节点配电网模型仿真计算，验证了该方法的有效性和准确性，并分析了节点相关性对潮流概率分布的影响。

概率潮流;节点相关性;配电网;Cholesky分解

1 引言

负荷随机波动、设备故障导致的网络结构变化等不确定因素使配电网的潮流分布具有一定的随机性。随着风力发电、太阳能发电等不可控的间歇式分布式电源(Distributed Generation，DG)大量并网，系统运行的不确定性进一步增加。概率潮流计算可以根据输入随机变量确定节点电压和支路潮流的概率分布，是分析有源配电网运行状态的重要工具［1］。

配电网运行中存在大量相关因素，概率潮流计算中输入随机变量具有较强的相关性。配电网是为城市、农村、矿区等局部地区供电的电网，网络地理尺度远小于输电网，相邻支路距离仅为几公里至十几公里［2］，不同节点之间的风速、光照强度等气候条件具有较强的相似性，因此配电网中同种DG出力具有相关性;同样，由于供电面积较小，区域内负荷性质相近，各节点负荷波动也存在一定相关性。而对于配电网同一节点，可以认为负荷及不同种类DG出力之间相互独立。作为配电网潮流计算中的输入随机变量，各节点注入功率之间的相关性与各节点功率、风速和光照强度等的相关性存在转换关系。

目前，概率潮流计算方法主要有蒙特卡洛模拟法、近似估计方法和解析法三类［3］。但上述方法均以输入随机变量相互独立为前提，因此需要对具有相关性的输入随机变量进行处理。文献［4］建立了风速的滑动自回归平均模型，通过时移技术处理风速相关性;文献［5］采用三阶多项式正态变换方法，将相关的随机变量等价变换到独立随机变量空间;文献［3，6］对相关系数矩阵进行Cholesky分解，将具有相关性的输入随机变量转化为独立随机变量或标准正态分布变量的线性组合。但上述方法均为面向输电网的相关性处理方法，且仅考虑了负荷或某种DG出力具有相关性的情况，并未针对配电网负荷和多种DG出力同时具有相关性、节点间相关性强的特点，给出相应的相关性处理方法。

本文结合配电网特点，以半不变量法为基础，由负荷、风速和光强相关性计算节点间注入功率相关性，通过Cholesky分解将节点间注入功率解耦为一组独立随机变量，进而给出了独立随机变量半不变量的计算方法，形成了适用于有源配电网的计及节点相关性的概率潮流算法。以蒙特卡洛模拟法为基准，通过对改造的部分IEEE 33节点配电网模型仿真计算，验证了该方法的有效性和准确性，并分析了节点相关性对潮流概率分布的影响。

2 分布式电源概率模型

2.1 风力发电概率模型

风速变化频率快、随机性强，国内外学者针对风速概率分布进行了多年统计研究，一般认为风速分布为正偏态分布。在风速的多种概率模型中，两参数的Weibull分布模型简单实用，对实际风速的拟合度较高［7］，其概率密度函数表达式为:

式中，v为风速;c和k分别为Weibull分布的尺度参数和形状参数，可以由风速统计数据的平均值μ和标准差σ近似求得［8］:

其中，Γ为Gamma函数。

在实测风速数据中，大部分风速数据都位于切入风速和额定风速之间，可以近似认为风机出力与实时风速为一次函数关系，则风机有功出力Pw的概率密度为:

式中，vci、vr分别为风机的切入风速和额定风速;Pr为风机的额定功率。

2.2 太阳能发电时序模型

根据统计，一段时间内太阳光照强度近似服从Beta分布［9］，其概率密度函数如下:

式中，r和rmax分别为这一时段内的实际光强和最大光强;α和β分别为Beta分布的形状参数，可以由光照强度统计数据的平均值μ和标准差σ近似求得［10］:

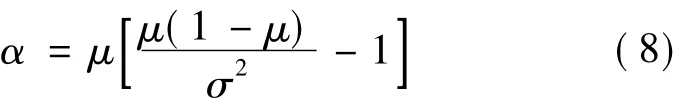
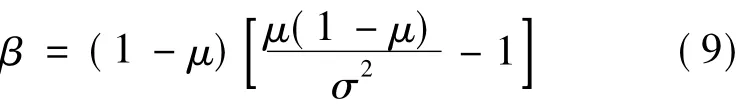
光伏阵列的输出功率与光强为一次线性关系:

式中，PM为光伏输出功率;A和η为太阳能电池板的面积和光电转换效率。将光伏阵列的额定功率计为RM，则光伏有功出力的概率密度函数为［11］:

3 计及随机变量相关性的概率潮流计算

以牛顿-拉夫逊潮流计算为基础，将极坐标形式的节点功率方程在基准运行点上泰勒展开，可以得到潮流方程的线性化模型:

式中，W为节点注入功率;X为节点电压幅值和相角等状态变量;下标0表示基准运行状态，即以各随机变量的期望值为输入量，进行确定性潮流计算确定的系统运行状态;记基准运行状态下的雅各比矩阵为J0，则S0=J－10，称为灵敏度矩阵。

在此模型中，状态变量的随机扰动是节点注入功率随机变量的线性和。当节点注入变量相互独立时，可以将随机变量的直接卷积运算简化为其各阶半不变量的代数运算，继而通过Gram-Charlier级数展开求得状态变量的概率分布［12］。

但是在有源配电网中，各节点负荷、风速和光强等具有较强的相关性，因此需对输入随机变量的相关性进行处理。

描述随机变量相关性的方法有多种，工程中常用的是相关系数矩阵。假设一组相关随机变量W =［w1，w2，…，wn］T的相关系数矩阵为CW:

式中，Cov(wi，wj)表示随机变量wi和wj的协方差; σi、σj表示wi、wj的标准差。

实际工程应用中，相关系数矩阵CW一般为正定矩阵，对该矩阵进行Cholesky分解［13］:

利用Cholesky分解得到的下三角矩阵B即可对相关随机变量W进行解耦，形成一组独立的等效随机变量Y［6］，如式(16)所示:

在已知随机变量W的基础上，通过式(16)可以转换为独立随机变量Y，进而W可以表示成Y的组合:

在如图1所示的配电网中含有n个复合节点单元(Composite Node Unit，CNU)，每个CNU包含随机波动的负荷，部分CNU中还含有一定容量的风力发电机组或光伏阵列。

图1 有源配电网及CNU示例Fig．1 Example of active distribution network and CNU

将节点注入功率计为W=［w1，w2，…，wn］T。同一节点处，负荷和风机、光伏的出力之间相互独立。根据同节点注入功率的可加性，有:

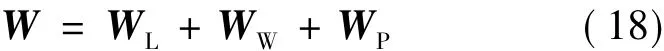
式中，WL、WW和WP分别表示节点负荷大小、风机出力和光伏出力向量(计注入系统功率为正，则负荷为负值。)。若第i个节点不含风机或光伏，则wWi=0或wPi=0。

方差和协方差具有下述性质［14］:

各节点之间，负荷或同种类别的DG出力具有相关性，假设W、WL、WW和WP对应的相关系数矩阵分别为CW、CWL、CWW和CWP，根据式(18)～式(20)可以推导出CW非对角元素CWij的计算公式:

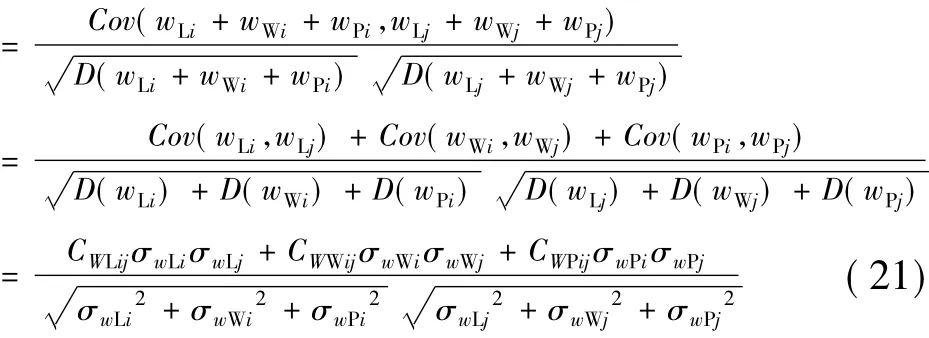
式(21)说明，各节点注入功率的相关系数矩阵可以由负荷和DG出力的相关系数矩阵及其标准差计算得到。

根据相关系数矩阵CW和式(15)～式(17)说明的解耦方法，将各节点注入功率W转换为一组独立的随机变量W'，如式(22)所示:

式中，BCW是对CW进行Cholesky分解得到的下三角矩阵。将式(22)代入式(12)，可得到解耦后的线性化潮流方程:

式(23)是由独立随机变量进行的线性运算，则W'的各阶半不变量可由式(25)得到:

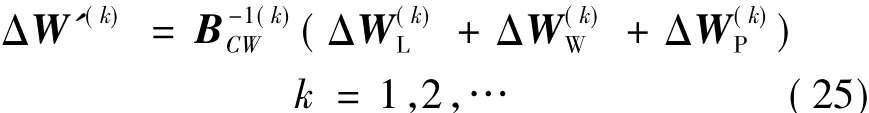
至此，已将相关的输入随机变量的概率潮流计算转换为独立输入随机变量的概率潮流计算，满足了使用半不变量法计算概率潮流的前提条件。将式(25)代入式(24)可得:

根据式(26)可以求出节点状态变量的各阶半不变量，进而通过Gram-Charlier级数展开求得状态变量的概率密度函数和累积分布函数等。

4 算例分析

4.1 算例系统说明

由于基于半不变量法的概率潮流算法计算误差一般不随系统规模的增大而增大［15］，本文为简化相关系数矩阵，以文献［2］给出的IEEE 33节点配点系统为基础，选取第1～3、18、19、22号节点及其连接线路构成规模较小的6节点配电网，并在各节点增加间歇式分布式电源构成CNU。配电网结构图如图2所示。

图2 有源配电网结构示意图Fig．2 Active distribution network structure diagram

网络线路参数参见文献［2］，各节点负荷和分布式电源参数如下:

(1)风力发电机型号为BWC Excel-R，额定功率7.5kW，切入风速3.5m/s、额定风速15m/s;太阳能电池组件型号为Pilkington SFM144，每个光伏阵列额定功率5kW，面积43.2m2、转换效率13.44%。风机和光伏的功率因数均取为cosφ=0.99(超前)。

各CNU配置风机和光伏阵列情况如表1所示。

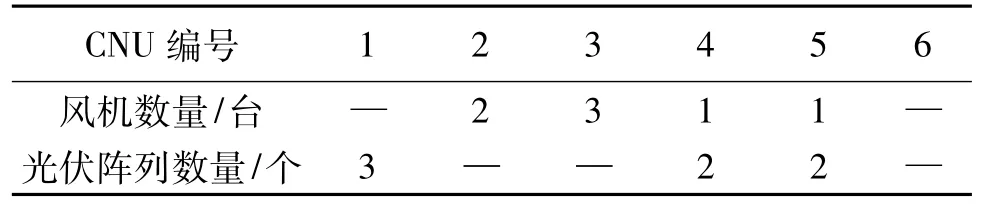
表1 各CNU中DG配置情况Tab．1 DG configuration in CNUs

(2)通过HOMER［16］软件对位于GMT+08∶00时区的中国天津市(东经117.20°，北纬39.13°)的风速和光照情况进行模拟，得到风速平均值μWind= 7.71m/s，标准差σWind=1.45m/s;光强平均值μSolar=0.168kW/m2，标准差σSolar=0.235kW/m2。

(3)负荷采用正态分布模型，负荷有功均值μP和无功均值μQ即为文献［2］中各节点有功和无功值，各节点有功负荷标准差统一确定为:σP=15kW，各负荷保持基准运行状态功率因数不变。

(4)各节点负荷、风速和光强的相关系数矩阵如式(27)～式(29)所示。

4.2 计算性能评估

以计及输入变量相关性的蒙特卡洛法对本算例的仿真结果作为本文所提方法准确性的判断依据。仿真发现，使用蒙特卡洛法对本算例仿真时，抽样次数超过10000次时，各节点电压、相角，各支路有功、无功的期望值变化率均小于0.1%，计算结果趋于稳定，因此采用10000次抽样的蒙特卡洛法仿真结果作为评判标准。

以1号支路末端的有功功率和1号节点电压幅值为例，比较本文方法与蒙特卡洛法计算结果。图3为上述两个输出变量的概率密度函数图像。

图3 两种方法下输出变量概率密度函数对比Fig．3 Comparison of output variable probability density function with twomethods

可以看到，本文所提方法可以求得各输出变量的概率分布，且计算结果与蒙特卡洛法标准结果基本吻合。为了量化本文方法计算的各输出变量的概率分布特征与标准方法的误差，选取所有节点电压幅值、相角和所有支路末端有功、无功的均值和标准差与标准方法比较，误差见表2。可以看到大部分指标误差均在1%以内，最大误差也小于2%。

表2 输出变量均值和标准差误差Tab．2 Error of output variables’mean and standard deviation单位:(%)

使用两种方法计算本算例所需时间如表3所示。相同仿真平台下，本文所提方法计算时间约为蒙特卡洛方法的1/354。

表3 计算时间对比Tab．3 Computation time comparison

4.3 输入变量相关性对系统运行的影响

为了研究节点间相关性对概率潮流计算结果的影响，选定三种典型情况:各节点间相关性满足式(26)～式(28)中相关系数矩阵的描述时为情况一;各节点负荷、风速和光照分别完全相关，即相关系数矩阵元素均为1时，为情况二;各节点完全独立，即相关系数矩阵均为单位矩阵时，为情况三。使用本文所提方法对上述三种情况下的本算例进行计算，以2号支路末端有功功率的概率分布为例研究节点相关性对系统概率潮流的影响。

图4展示了三种相关性下2号支路有功功率的概率分布情况。三条曲线的集中位置和分布趋势基本相同，说明相关性并不影响输出变量的期望、概率分布类型和畸变程度;但三条曲线概率分布在均值附近的离散程度具有明显不同，说明相关性对输出变量的标准差影响较大。表4定量说明了这种情况:从节点间完全独立到完全相关，输出变量的平均值增加了0.88%，而标准差增加了74.03%。

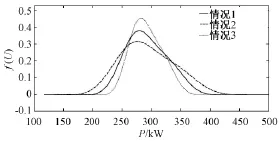
图4 不同相关性下2号支路有功的概率密度函数Fig．4 Probability density function of No．2 branch active power with different correlations

表4 不同相关性下2号支路有功的均值和标准差Tab．4 Mean and standard deviation probability density function of No．2 branch active power with different correlations

计算结果显示，支路有功、节点电压幅值和相角与节点相关性之间也存在类似关系。说明节点间相关程度越大，节点电压和支路潮流的波动性越大。这是由于节点相关性较强时，负荷和同种DG出力的波动情况分别趋于一致(负荷同时出现峰值或谷值，风机同时多发或少发等)，造成电压越限率增加，线路轻载和重载时间增长，系统功率峰谷差增大。尤其是在配电网中，供电范围较小，不同节点的气候条件和用电情况相对一致，更有可能出现上述情况。因此在配电网规划中，应合理配置DG类别，在同一节点安排多种类型DG配合工作，并充分利用储能装置以及柴油发电机、燃气轮机等出力可控的DG，降低节点相关性，优化配电网潮流。

5 结论

针对有源配电网节点相关性特点，本文提出了一种基于半不变量法的配电网概率潮流计算方法，重点分析了节点注入功率相关性与负荷、风速和光强等随机变量相关性的转换关系，给出了解耦后独立随机变量半不变量的计算方法。通过算例仿真，考察了所提方法的运算性能，并分析了输入变量相关性对系统运行特性的影响。结论如下:

(1)采用本文方法进行概率潮流计算时，可以同时考虑负荷、风速和光强等多个随机变量具有相关性的情况，更符合有源配电网实际情况。

(2)本文方法计算准确性较高，与蒙特卡洛法相比计算时间大为缩短，具有较好的工程应用前景。

(3)节点间相关性增强会显著增加节点电压和支路潮流的波动程度，在配电网规划中应合理配置DG类型，降低节点相关性。

参考文献(References):

［1］王锡凡，王秀丽(Wang Xifan，Wang Xiuli)．电力系统的随机潮流分析(Probabilistic load flow analysis of power system)［J］．西安交通大学学报(Journal of Xi’an Jiaotong University)，1988，22(3):87-97．

［2］王守相，王成山(Wang Shouxiang，Wang Chengshan)．现代配电系统分析(Modern distribution system analysis)［M］．北京:高等教育出版社(Beijing:Higher Education Press)，2007．

［3］陈雁，文劲宇，程时杰(Chen Yan，Wen Jinyu，Cheng Shijie)．考虑输入变量相关性的概率潮流计算方法(Probabilistic load flow analysis considering dependencies among input random variables)［J］．中国电机工程学报(Proceedings of the CSEE)，2011，31(22):80-87．

［4］范荣奇，陈金富，段献忠，等(Fan Rongqi，Chen Jinfu，Duan Xianzhong，et al．)．风速相关性对概率潮流计算的影响分析(Impact of wind speed correlation of probabilistic power flow)［J］．电力系统自动化(Automation of Electric Power Systems)，2011，35(4):18-22．

［5］杨欢，邹斌(Yang Huan，Zou Bin)．含相关性随机变量的概率潮流三点估计法(A three-point estimate method for solving probabilistic power flow problems with correlated random variables)［J］．电力系统自动化(Automation of Electric Power Systems)，2012，36 (15):51-56．

［6］石东源，蔡德福，陈金富，等(Shi Dongyuan，Cai Defu，Chen Jinfu，et al．)．计及输入变量相关性的半不变量法概率潮流计算(Probabilistic load flow calculation based on cumulantmethod considering correlation between input variables)［J］．中国电机工程学报(Proceedings of the CSEE)，2012，32(28):104-113．

［7］丁明，吴义纯，张立军(Ding Ming，Wu Yichun，Zhang Lijun)．风电场风速概率分布参数计算方法的研究(Study on the algorithm to the probabilistic distribution parameters ofwind speed in wind farms)［J］．中国电机工程学报(Proceedings of the CSEE)，2005，25(10): 107-110．

［8］李自应，王明，陈二永，等(Li Ziying，Wang Ming， Chen Eryong，et al．)．云南风能可开发地区风速的韦布尔分布参数及风能特征值研究(Study of Weibull distributing parameters and wind energy characteristic value of windspeed around the parts of Yunnan in which the wind energy can be developed)［J］．太阳能学报(Acta Energiae Solaris Sinica)，1998，19(3):248-253．

［9］Karaki SH，Chedid R B，Ramadan R．Probabilistic performance assessmentof autonomous solar-wind energy conversion systems［J］．IEEE Transactions on Energy Conversion，1999，14(3):766-772．

［10］Abouzahr I，Ramakumar R．Loss of power supply probability of stand-alone photovoltaic systems:a closed form solution approach［J］．IEEE Transactions on Energy Conversion，1991，6(1):1-11．

［11］王成山，郑海峰，谢莹华，等(Wang Chengshan，Zheng Haifeng，Xie Yinghua，et al．)．计及分布式发电的配电系统随机潮流计算(Probabilistic power flow containing distributed generation in distribution system)［J］．电力系统自动化(Automation of Electric Power Systems)，2005，29(24):39-44．

［12］郑海峰(Zheng Haifeng)．计及分布式发电的配电系统随机潮流计算(Probabilistic power flow containing distributed generation in distribution system)［D］．天津:天津大学(Tianjin:Tianjin University)，2006．

［13］杨明，刘先忠(Yang Ming，Liu Xianzhong)．矩阵论，第二版(Matrix theory，2nd edition)［M］．武汉:华中科技大学出版社(Wuhan:Huazhong University of Science＆Technology Press)，2005．

［14］盛骤，谢式千，潘承毅(Sheng Zhou，Xie Shiqian，Pan Chengyi)．概率论与数理统计，第四版(Probability theory and mathematical statistics，4th edition)［M］．北京:高等教育出版社(Beijing:Higher Education Press)，2010．

［15］胡泽春，王锡凡(Hu Zechun，Wang Xifan)．基于半不变量法的随机潮流误差分析(Error analysis of the probabilistic load flow based on cumulantmethod)［J］．电网技术(Power System Technology)，2009，33(18): 32-37．

［16］Homer．The optimization model for distributed power［EB/OL］．http://www．homerenergy．com/，2013．

(，cont．on p.51)(，cont．from p.37)

Probabilistic load flow considering correlations among nodes of distribution network w ith batch distributed generation

LIU Hong1，GE Shao-yun1，ZHANG Xin2，MA Kang3，LIU Jun3
(1．Key Laboratory of Smart Grid(Tianjin University)，Ministry of Education，Tianjin 300072，China; 2．Electric Power Research Institute of State Grid Tianjin Electric Power Corporation，Tianjin 300384，China; 3．China Electric Power Research Institute，Beijing 100192，China)

Probabilistic load flow calculation is an important tool to analyze the operating state of distribution network．Currently the probabilistic load flow calculation of distribution network with batch distributed generation is facing to new problems．Differing from the large scale transmission network，there are strong correlations among load characteristics，climatic conditions and othermultiple variables of distribution network nodes．Aimed at this situation the calculation method of node injected power correlation is proposed．Then node injected power is decoupled with the Cholesky decomposition，converting the distribution network probabilistic load flow calculation to the calculation with uncorrelated input random variables．Hence probabilistic load flow calculation method considering the correlation among nodes for active distribution network is formed．The effectiveness and accuracy of the proposed method are proven by the comparative tests in the part ofmodified IEEE 33-bus distribution network．The impacts of node correlation on load flow probabilistic distribution are investigated by the proposed method．

probabilistic load flow;node correlation;distribution network;Cholesky decomposition

TM72

A

1003-3076(2015)06-0032-06

2013-09-18

国家自然科学基金资助项目(51107085)、国家电网公司科技项目“提高配电网故障处理能力的关键技术研究与开发”(2012-094)

刘洪(1979-)，男，天津籍，讲师，博士，主要从事城市电网规划、评估等方面的研究和应用工作;张鑫(1988-)，男，河北籍，工程师，硕士，主要从事配电网规划与概率潮流计算方面的研究工作(通信作者)。